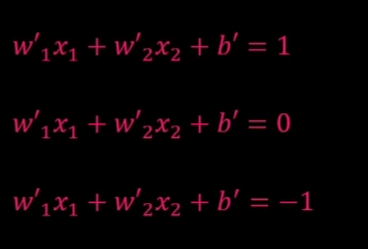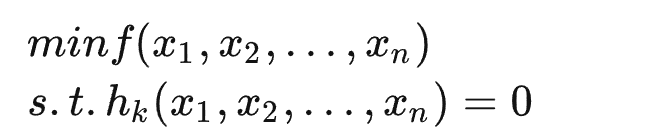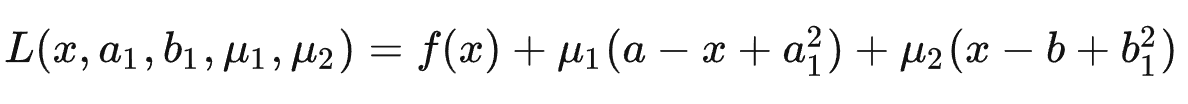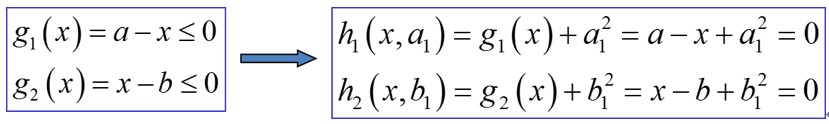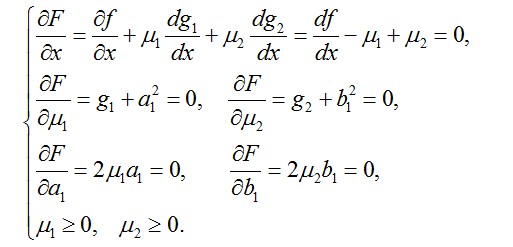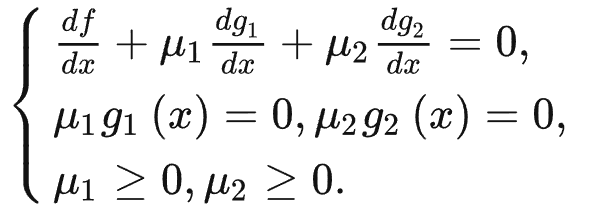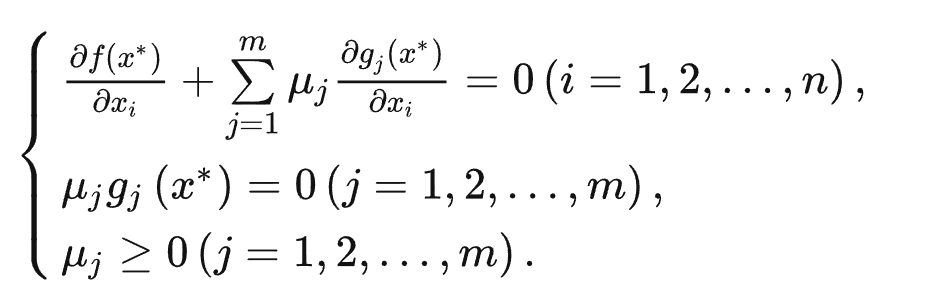线性可分
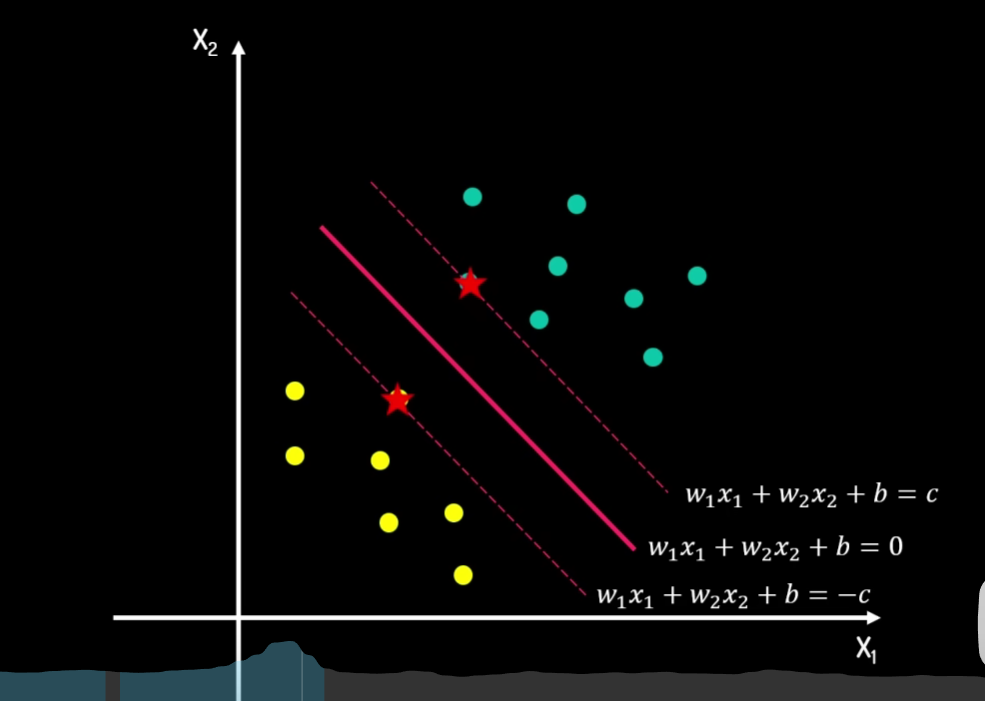
找到一个比较好的分割器,即一个超平面(Hyper Plane)。需要最大化之间的 margin。
是支持向量:y(wTx+b)=1,不是支持向量:y(wTx+b)>1。
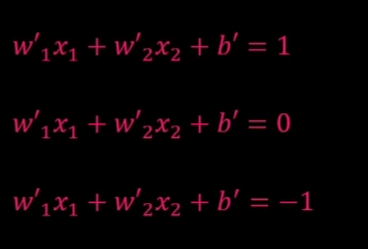
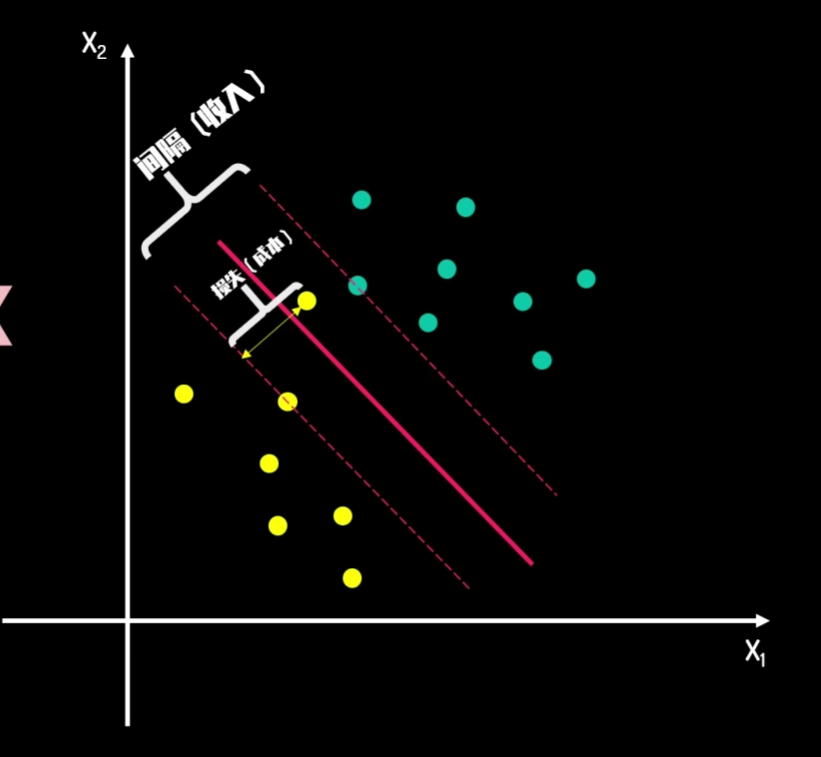
升维转换和核技巧

转换为:
minimize ∣∣w∣∣,s.t. yi×(w⋅xi+b)≥1,其中 yi 代表点的类型,取值 −1,1。
如果是等式,可以使用拉格朗日乘子法,但是这里是不等式,所以引入变量 pi,转化为:
yi×(w⋅xi+b)−1=pi2
L(w,b,λi,pi)=2∣∣w∣∣2−i=1∑sλi×(yi×(w⋅xi+b)−1−pi2)
对 w,b,λi,pi 求偏导,得到:
w−i=1∑sλiyixi=0
−i=1∑sλiyi=0
yi×(w⋅xi+b)−1−pi2=0
2λipi=0
推出:λi=0 或 pi=0。
得到
yi×(w⋅xi+b)−1≥0,λi=0
或
yi×(w⋅xi+b)−1=0,λi=0
KKT 条件 Karush–Kuhn–Tucker conditions
−i=1∑sλiyi=0
w−i=1∑sλiyixi=0
λi(yi×(w⋅xi+b)−1)=0
λi≥0,yi×(w⋅xi+b)−1≥0
有条件极值的 Lagrange 乘数法
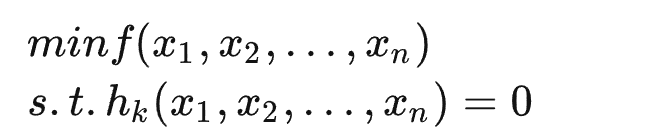
有不等式的 Lagrange 函数
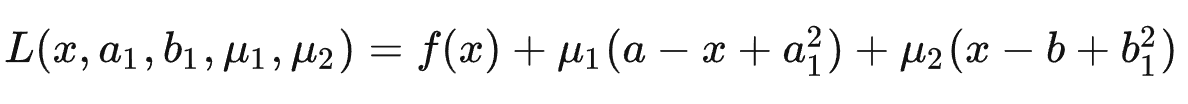
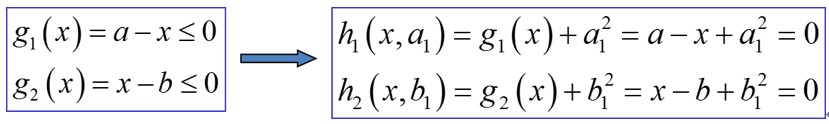
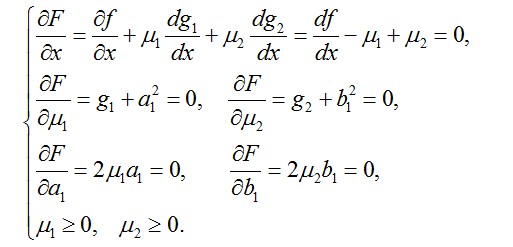
- μ1=0,a1=0,等于 g1 约束不起作用。
- μ1=0,a1=0,等于约束 g1 起作用,而且必须要求 g1=0。
这其实就是代表了取极值一定需要某个约束最靠近边界,或舍弃某个约束。
于是转化为:
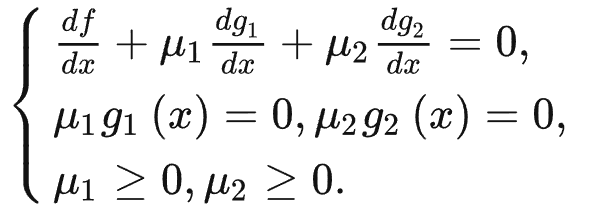
对于多元多次不等式来说,形式如下:
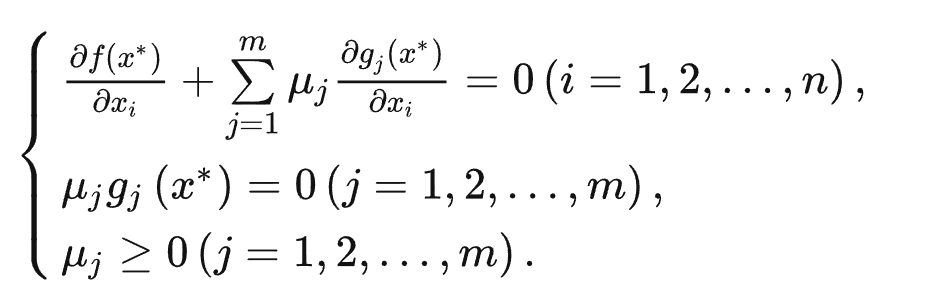
−∇f(x∗)=j∈J∑μj∇gj(x∗)
其中 J 代表起约束作用的集合。
可以看做梯度向量 −∇f(x∗) 由 ∇gj(x∗) 线性组合而成。而往下走,就需要 −∇f(x∗)>0,因此组合系数 μj 应该 ≥0。
因此,要判断解 x∗ 是否最优,只需要代入以上表达式即可。
拉格朗日对偶性
广义拉格朗日函数
L(x,α,β)=f(x)+i=1∑kαici(x)+j=1∑lβjhj(x)
其中 α,β 是向量。
考虑
θP(x)=α,β;αi≥0maxL(x,α,β)
当 x 满足问题约束时,x 满足 KTT 条件,因此,αici(x)=0,hj=0。
θP(x)=f(x)
因此问题等价于
xminθP(x)=xminα,β;αi≥0maxL(x,α,β)
原问题的最优值:
p∗=xminθP(x)
对于对偶问题,我们首先定义:
θD(α,β)=xminL(x,α,β)
再考虑:
α,β;αi≥0maxθD(α,β)=α,β;αi≥0maxxminL(x,α,β)
对偶问题的最优值:
d∗=α,β;αi≥0maxθD(α,β)
则:
d∗=α,β;αi≥0maxxminL(x,α,β)≤xminα,β;αi≥0maxL(x,α,β)=p∗
原因是先作用 max,结果一定大。
我们有定理:
假设函数 f(x) 和 ci 是凸函数,而且不等式约束 ci(x) 严格可行,则:
p∗=d∗=L(x∗,α∗,β∗)
称为满足强对偶条件。
SVM 中的拉格朗日对偶性
对于每个 λi,
q(λi)=minmize(L(w,b,λi))=minmize(f(w)−i=1∑sλigi(w,b))
对于最优解 w∗,b∗,
q(λi)≤f(w∗)−i=1∑sλigi(w∗,b∗)
根据 λi≥0,gi(w∗,b∗)≥0,
很多 q(λi),里面存在一个最优值,因此我们寻找 λi∗
q(λi)≤q(λi∗)≤f(w∗)≤f(w)
对偶问题:
maximize q(λi)=maximize(minimize(L(w,b,λi)))。
s.t. λi≥0。
等号成立,强对偶成立。
对对偶问题的化简
首先,由 w−∑i=1sλiyixi=0,代入原式,再注意到 ∑i=1sλiyi=0,可以消掉常数项 b,最终得到:
λimax=λimax(I=1∑sλi−21i=1∑sj=1∑sλiλjyiyjxi⋅xj)
然后代会求得 w,然后由 w,就可以求解 b。
Kernel Trick
原维度向量 x 转换为新维度向量 T(x)。
λimax=λimax(I=1∑sλi−21i=1∑sj=1∑sλiλjyiyjT(xi)⋅T(xj))
定义 K(xi,xj)=T(xi)⋅T(xj)。

多项式核函数。
高斯核函数 RBF
K(xi,xj)=e−γ∣∣xi−xj∣∣2
γ 越小,相似度越大,越容易被分割。
可以发现 K(xi,xj) 展开式中包含
exi⋅xj
因此,对于泰勒展开来说,包含了无穷项 xi⋅xj。
软间隔最优化问题
wmin2∣∣w∣∣2+C×i=1∑sεi
其中
εi=max(0,1−yi×(w⋅xi+b))