这两个”根“在多项式乘法里面运用非常广泛。
单位根(FFT)
关于我自己对单位根的理解。
单位根其实就是一些复数,他们的模长为1。
所以单位根一定在单位圆上
假设一个单位根z的极角为θ,那么我们可以将z表示为cosθ+isinθ
数形结合考虑,从圆上某一个点做一条垂线,那么垂线长度为sinθ,垂足到原点距离为cosθ
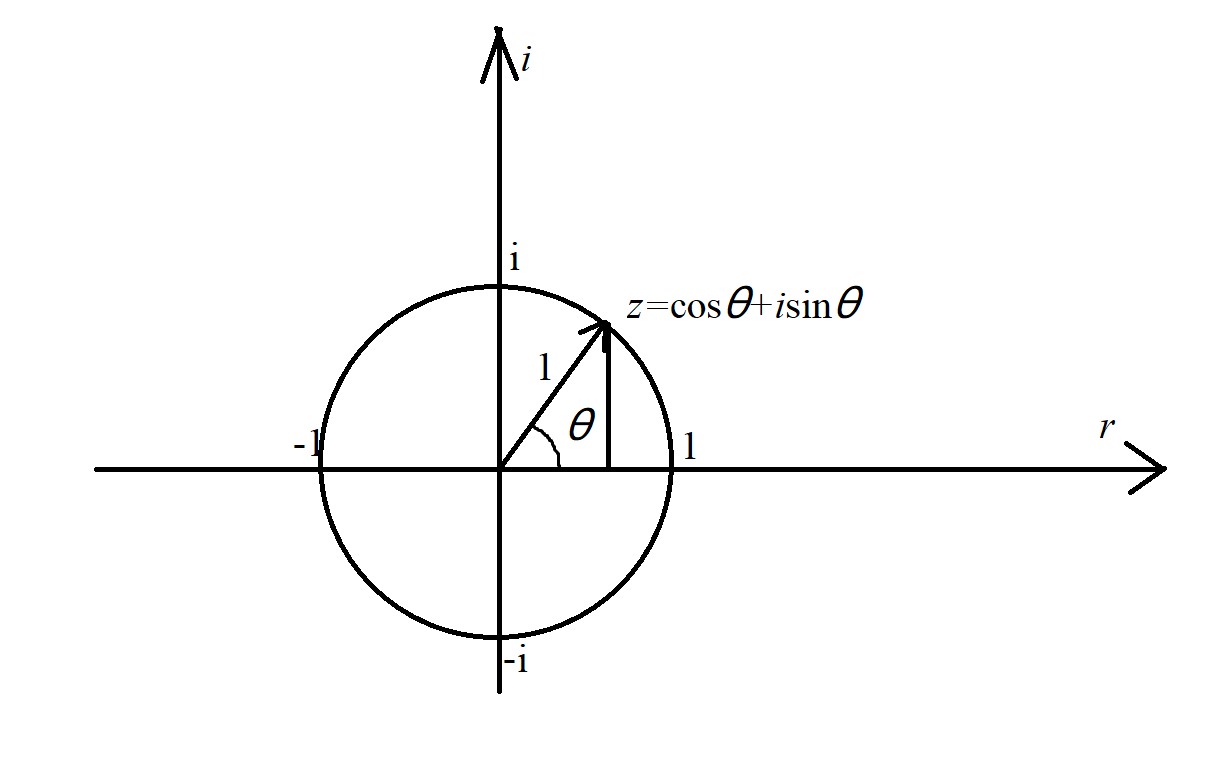
考虑使用向量模长验证,∣z∣=sin2θ+cos2θ=1
ωnk=cosnk2π+isinnk2π
感性地理解这个式子,注意到2π为360°,所以这个式子的意义就是将单位圆用一些经过圆心的线分成n份,从1+0i往逆时针数k次,数到的线的端点所代表的复数。

于是发现四个推FFT所用的经典的式子都非常naive
1.ωnk=ω2n2k
这个代表的意思就是把单位圆分成n份,数k次,和分成2n份,数2k次所代表复数是一样的。非常智障。
也可以通过三角函数证明:
ωnk=cosnk2π+isinnk2π=cos2n2k2π+isin2n2k2π=ω2n2k
2.ωnk+2n=−ωnk
定义:对于复数z=a+bi,−z=−a−bi
这个也非常好理解,n/2代表半圈,所以这个式子的意思是从编号为k的复数开始走半圈,代表的复数和之前的正好相反(实部和虚部都相反)
3.ωn0=ωnn=1,ωn2n=−1
编号为0和编号为n的点代表的复数相等,都为1+0i,编号为n/2的点其实就是1+0i转过半圈,就是−1+0i
4.ωnp×ωnq=ωnp+q
复数的乘法其实像三角函数一样,设z1=a1+ib1,z2=a2+ib2
根据复数乘法定义,那么我们有z1×z2=(a1×a2−b1×b2)+i(a1×b2+a2×b1)
我们有三角函数的合角公式:
sin(A+B)=sinAcosB+cosAsinB
cos(A+B)=cosAcosB−sinAsinB
换元:α=np2π,β=nq2π
于是ωnp=cosα+isinα
还有ωnq=cosβ+isinβ
于是ωnp×ωnq=(cosαcosβ−sinαsinβ)+i(sinαcosβ+cosαsinβ)=cos(α+β)+isin(α+β)=ωnp+q
(吐槽一句,复数的乘法好像就是为了这个东西定义的)
这个式子要好好体会。
有了第四个式子,我们就可以再推出第三个式子:
ωnk+2n=ωn2n×ωnk=(−1+0i)×ωnk=−ωnk
原根(NTT)
有时候题目要求对一个大质数取模,这时就不能用单位根,要用原根。
p的原根是满足g0%p,g1%p,g2%p...gp−2%p恰好等于[1,p−1]中的所有数的最小的g。

现实中,可以从2→p−1枚举g,如果满足gpip−1!=1(modp)均成立,那么我们就找到了p的原根。
我们称gn为n的原根,那么我们也得到了类似于ωnk一长串的gn0,gn1,gn2,...,gnn−2,而且他们模意义下和[1,p−1]中的所有数一一对应。
我们设一个素数p=a×2b+1
有以下等价关系:gn=gnp−1⇔ωn=cosn2π+isinn2π。(下面证明)
并且有gnk=gnp−1×k
显然有gnp×gnq=gnp−1×(p+q)=gnp+q。
1.g2n2k=gnk
显然,g2n2k=g2np−1×2k=gnp−1k=gnk。
2.gn2n=−1,gn0=gnn=1
显然gn0=g0=1,gnn=gp−1=1(modp)。
因为(gn2n)2=gnn=1
得gn2n=±1。
又因为gnn!=gn2n,且gnn=1,所以gn2n=−1。
3.gnk+2n=−gnk
上面的式子套入p=k,q=2n,显然。






