回归 Regression

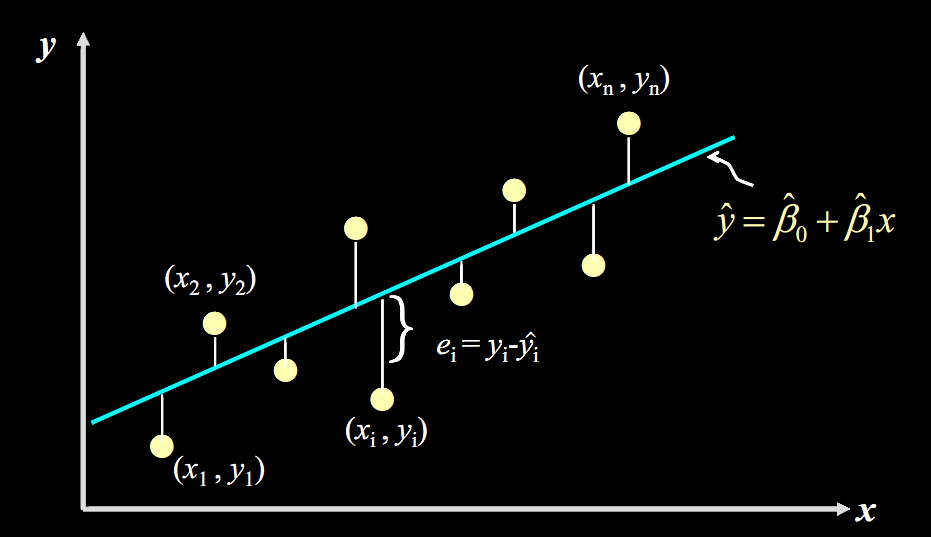要求我们最小化损失函数残差平方和（Sum of Squares for Error)

Q=\sum_{i=1}^n (y_i-\hat y_i)^2

而用线性函数 $\hat y=\beta_0+\beta_1 x$ 去拟合这条直线。

我们研究函数 $Q=F(\beta_0,\beta_1)$ ，发现其是两个二次函数“叠加”在一起形成的。

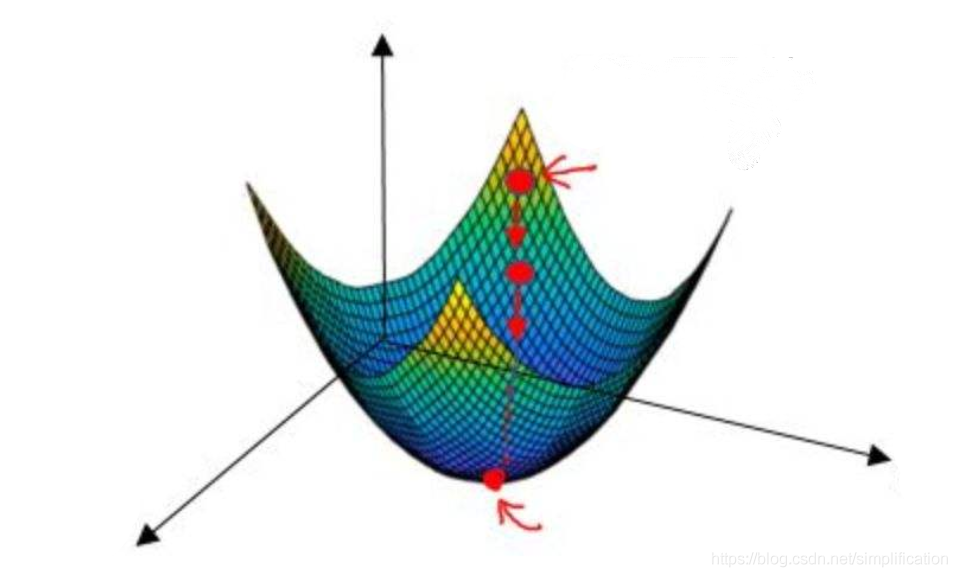
于是，我们试图找到其偏导数为 $0$ 的点：

\frac{\part Q}{\part \beta_0}=0,\frac{\part Q}{\part \beta_1}=0

这里，我们可以使用梯度下降（Gradient descent）的方法，类似于牛顿迭代法，我们下一次选择的点与当前点的偏导数有关，不同的是，在牛顿迭代中，我们选取当前函数值 $f(x)$ ，除以导数，而在梯度下降法中，我们选取学习率 $\gamma$ 与偏导数相乘，得到偏移大小，

梯度下降法的几何解释：

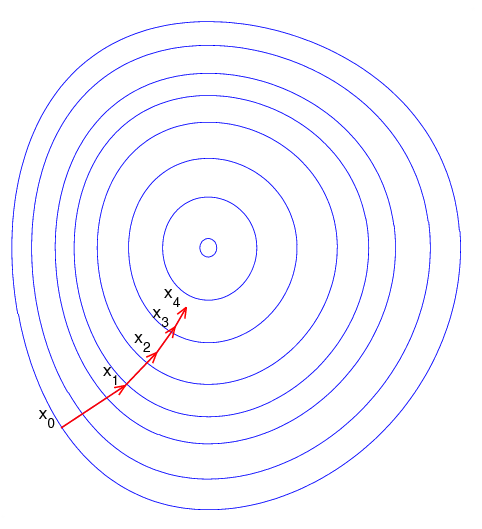
假设我们现在要爬山，我们看正北方向，如果是上升的，则去往正北方向，上升地越快，正北方向的速度分量越多，正东方向也是如此。

缺点是梯度下降法会陷入局部最优解，而且如果 $\gamma$ 选择不好的话，会出现迭代较慢或者反复横跳的情况，因此， $\gamma$ 应该动态地选择，具体来说，第 $t$ 轮迭代，可以选择 $a/\sqrt{t+1}$ 之类的值。

y=\beta_0+\beta_1x_1+\cdots+\beta_px_p

多元线性回归也可以用主成分分析解决。