分类 Classification

回归需要我们输出连续性的结果，如给出房屋的面积，求房屋的价格。
分类需要我们输出离散型的结果，如给出一个手写的汉字，输出这个汉字的编码。

Logistic Regression 逻辑斯蒂回归

我们考虑用回归的方法解决分类的问题，如，对于一个顾客来说，买房和不买房取决于房屋的价格，我们记录多位用户买房的行为，可以得到房价和一个 $0,1$ 二元结果的对应关系。

我们可以考虑用线性回归去拟合二元的结果，如：

\hat y=1,\beta_0+\beta_1x>0.5;0,\beta_0+\beta_1x\le0.5

事实上，逻辑斯蒂回归使用的是 sigmond 函数：

\sigma(z)=\frac{1}{1+\exp(-z)}

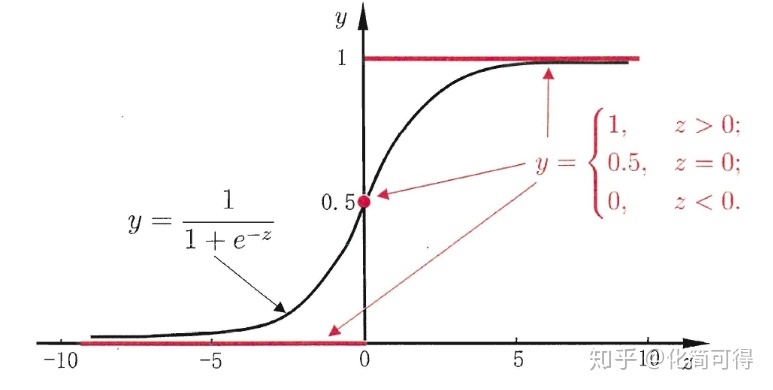
相对于上面的二元函数更加平滑，适合预测概率。

令 $x_i\beta=\beta_0+\beta_1x_{i1}+\cdots+\beta_px_{ip}$

于是，我们希望

P(y=1|x,\beta)=\sigma(x\beta)

定义似然函数

\mathcal L(\beta)=\prod_{i=1}^n P(y_i|x_i,\beta)

也就是要这个 $\beta$ 对应的概率最大。

取对数后，我们得到：

\log \mathcal L(\beta)=\sum_{i=1}^n (y_i \log \sigma(x_i\beta)+(1-y_i)\log (1-\sigma(x_i\beta)))

我们定义损失函数：

J(\beta)=-\log \mathcal L(\beta)

因为我们希望对应概率尽量大，也就是负数尽量小。

梯度下降求解：

\frac{\part J(\beta)}{\part \beta_j} = \sum_{i=1}^n (\sigma(x_i\beta)-y_i) \times x_{ij}

因此，代码如下：

for (int t=1;t<=iter;++t){
    Matrix y_posi=sigmoid(X*beta.transpose());
    long double cross_entropy=-mean(mul(Y,log(y_posi))+mul(flip(Y),log(flip(y_posi,1e-4))));
    Matrix grad=(Y-y_posi).transpose()*X;
    beta=beta+alpha*grad;
}

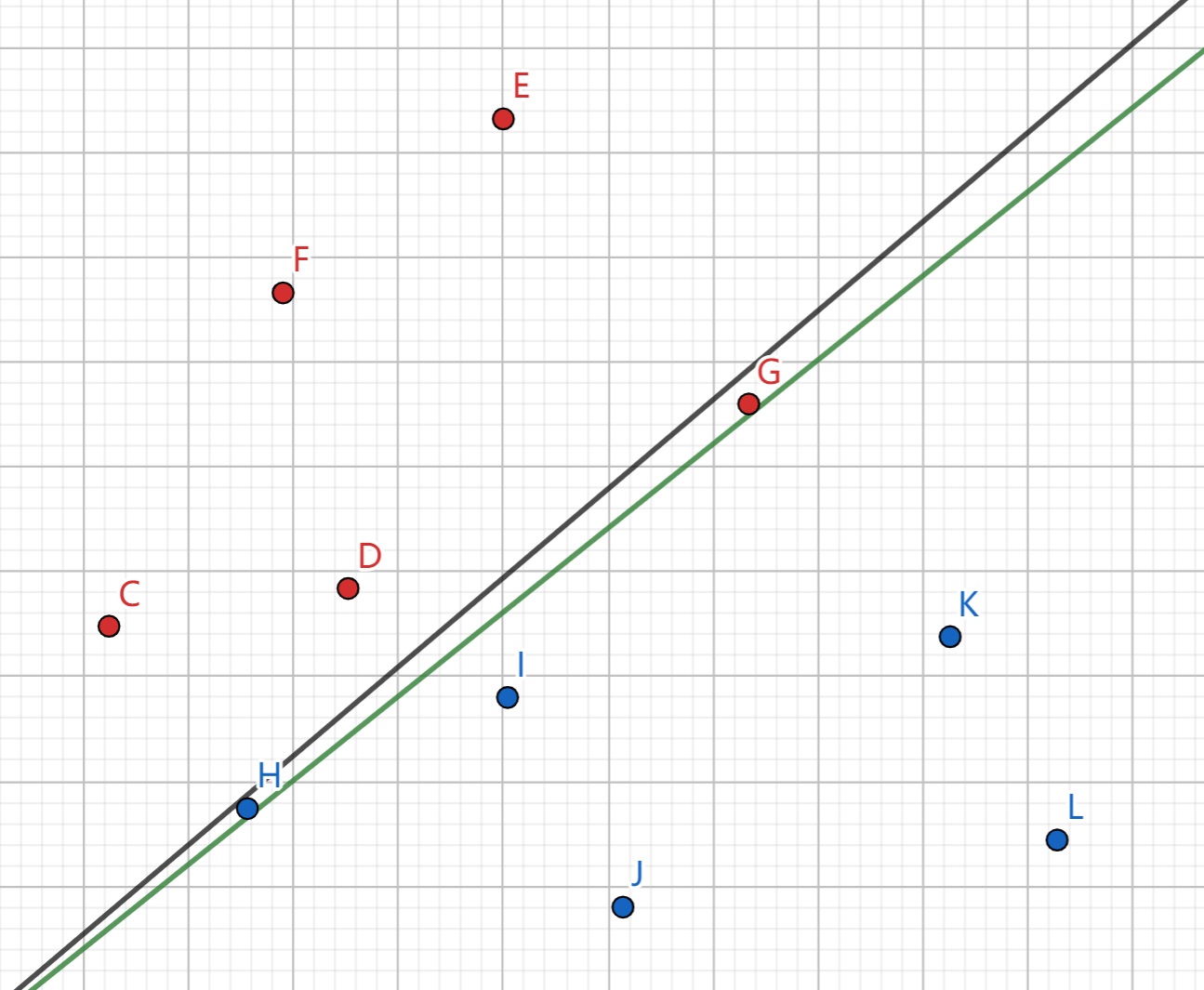
例如，利用 logistic 模型，我们就可以划一条直线，将两种不同颜色的数据点分开。

得出的 $\sigma(x\beta)$ 就是为红点的概率，如输出：

代表回归模型认为在 ABCD 四个点几乎能肯定是红点，IJKL 几乎是蓝点，但是不太好区分 HG 两个点。

而如果我们引入常数项，将每个点改写为 $(1,坐标x,坐标y)$ 的形式，则可以发现能够非常好地匹配：

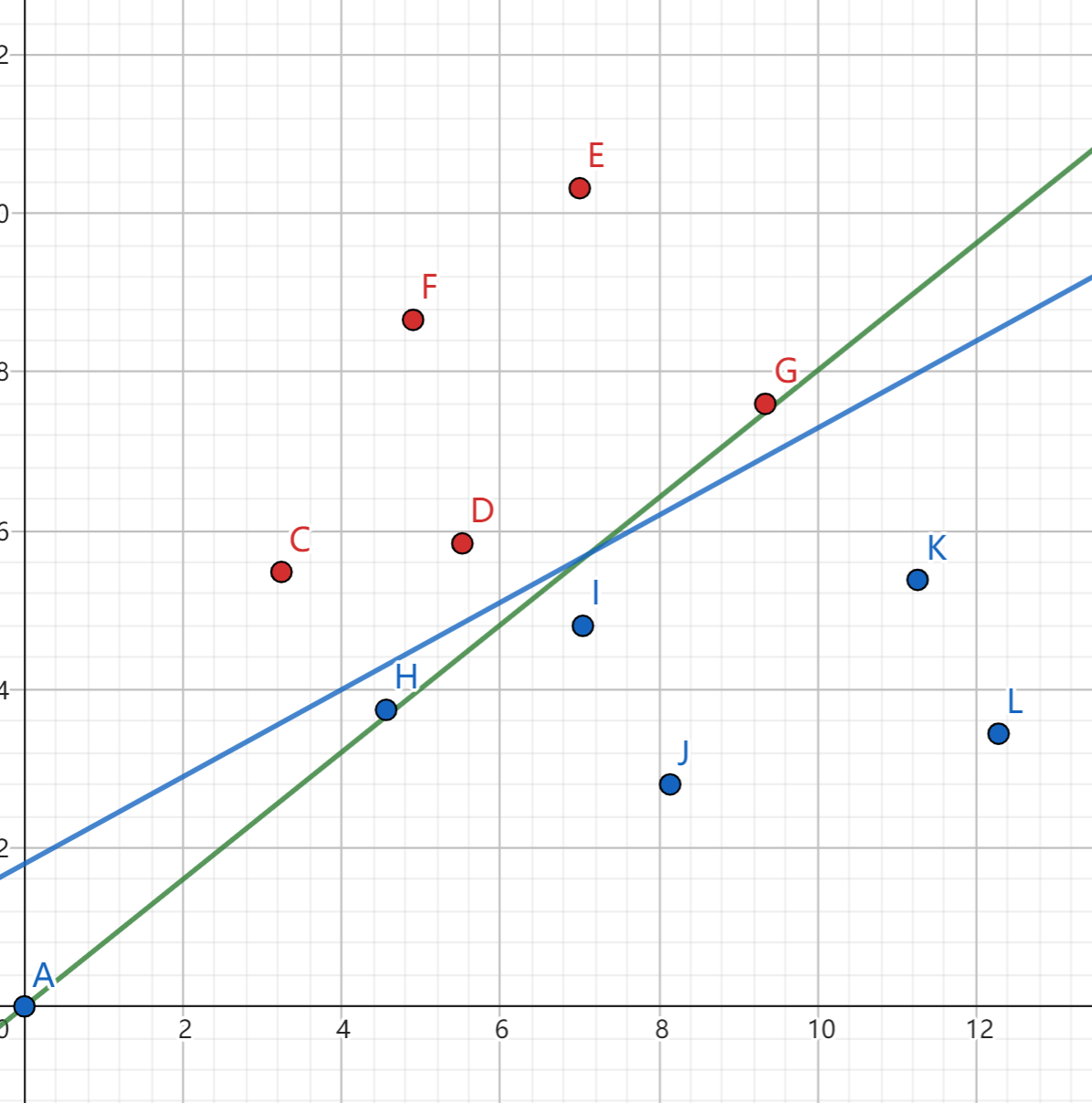
$\beta$ 迭代完成为 -10.1665 -3.10623 5.6517。

则直线方程表示为 $5.6517 y-3.10623 x-10.1665=0$ ，概率：