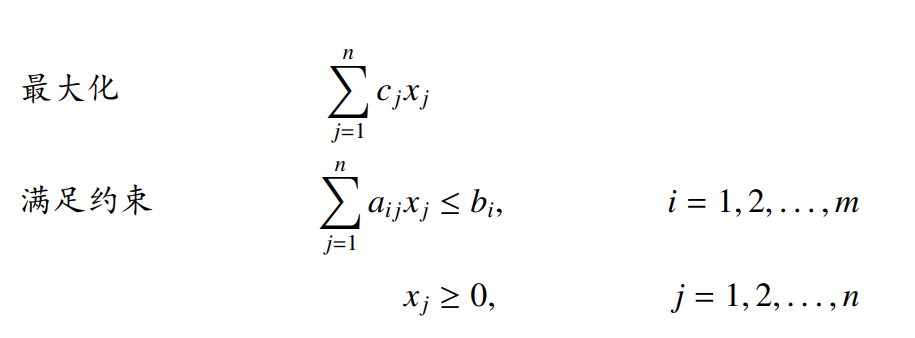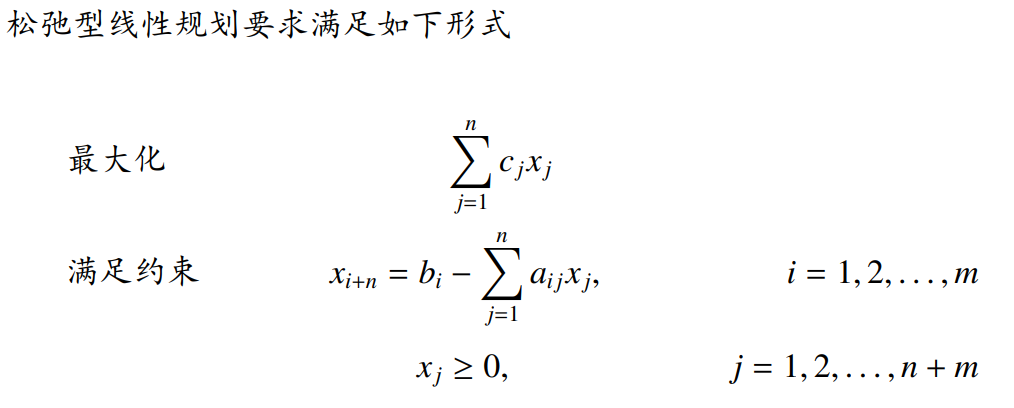单纯形算法

线性规划的一般形式

标准型线性规划

标准形的特征：极小化、等式约束、变量非负

松弛型线性规划

解空间是凸集，参见[[凸集]]

单纯形

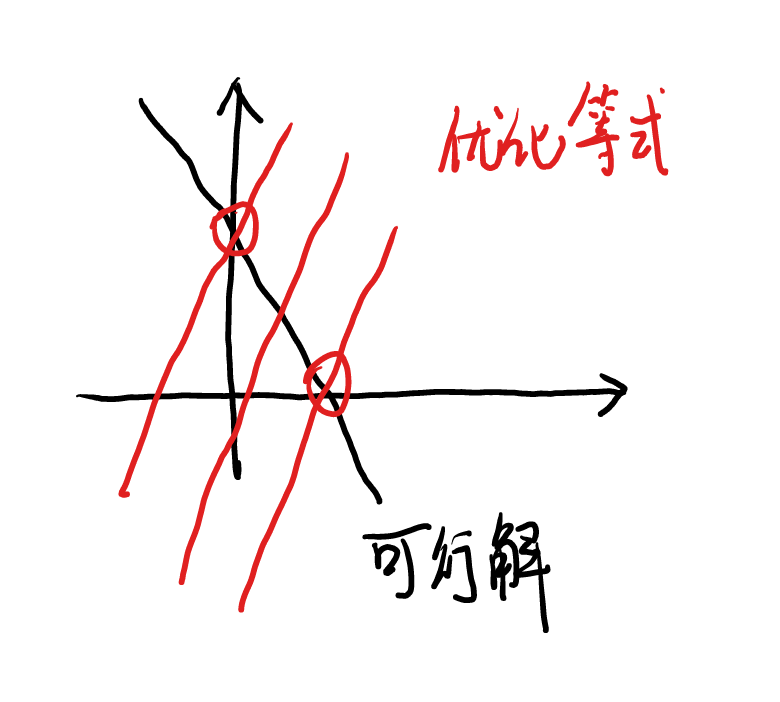
单纯形法的基本思想是，通过变量的代换，实现在解空间内沿着边界朝着目标函数增大的方向移动。其核心操作是转轴(pivot) 操作，即变量的代换。

定义 设 B 是 A 的m个线性无关列组成的矩阵， 置其余列所对应的变量为零，称所得方程组的解是 Ax = b 的基本解(basic solution) ;非负基本解是标准形问题的基本可行解(basic feasible solution,bfs).

称 B 是基(basis)；
称与 B 的列对应的变量为基变量(basic variables)

基本可行解的个数不超过

$\binom{n}{m}$

初始化：如何找到一个BFS？
判断准则：何时最优？何时无界？
迭代规则：如何从一个极点/BFS迭代到相邻极点/BFS？

线性规划基本定理

如何直观地理解这件事情，我们考虑 $m=1,n=2$ 的情况，最优解只可能 $x=0$ 或 $y=0$。

再考虑严谨地证明这件事。

考虑具有标准形的线性规划问题，其中 $A$ 是秩为 $m$ 的 $m×n$ 矩阵, 如果问题有解，则必有某个基本可行解是最优解.

考虑到任何 $A$ 中的列向量都能被 $B$ 中的列向量线性表示，如果在某个最优解中 $x_j>0$，考虑到列向量 $a_j=[k_1,k_2,\cdots,k_m]B$，因此对 $B$ 列向量对应的 $x$ 系数操作，就可以得到一个基本可行解。

转轴操作

选择基变量 $x_B$ 和非基变量 $x_N$，将其互换，具体来说，一开始有：

$x_B=b_i-\sum_{i=1}^n a_{ij} x_j$

那么：

$x_N=(b_i-\sum_{j\not=N}a_{ij}x_j-x_B)/a_{iN}$

要保证 $a_{iN}\not=0$，否则解不出 $x_N$。

Simplex 操作

Simplex操作即单纯形算法的主过程，从一个基本解出发，经过一系列的转轴操作，达到最优解。通过选择特定的换入变量以及换出变量，可以使得每一次转轴操作都能使目标函数增大，直到达到全局最优解。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

double Simplex(Matrix<double>A,Matrix<double>b,Matrix<double>c){
    Matrix<double>M=addV(addH(c,Matrix<double>(1,1)),addH(A,b));
    int n=A.col,m=A.row;
    Matrix<int>isBasic(1,n);
    for (int i=n-m+1;i<=n;++i) isBasic(i)=true;
    int last=n+1;
    while (true){
        // std::cout<<M<<std::endl;
        int e=0;
        for (int i=1;i<=n;++i){
            if (!isBasic(i)&&M[1][i]>0){
                e=i;
                break;
            }
        }
        if (e==0){
            return -M[1][last];
        }
        int pos=0;
        double min_f=0;
        for (int i=2;i<=m+1;++i){
            if (M[i][e]>0){
                if (pos==0||M[i][last]/M[i][e]<min_f){
                    pos=i;
                    min_f=M[i][last]/M[i][e];
                }
            }
        }
        // std::cout<<pos<<std::endl;
        if (pos==0){
            return INFINITY;
        }
        else{
            int l=0;
            for (int i=1;i<=n;++i){
                if (isBasic(i)&&equals(M[pos][i],1.0)){
                    l=i;
                    break;
                }
            }
            // std::cout<<"leave "<<l<<" enter "<<e<<std::endl;
            isBasic(l)=false;
            isBasic(e)=true;
            M.times('R',pos,1/M[pos][e]);
            for (int i=1;i<=m+1;++i){
                if (i!=pos){
                    M.addtimes('R',pos,-M[i][e],i);
                }
            }
        }
    }
}

单纯形的应用

最大流问题

人为增加一条从 $t$ 到 $s$ 的流量无穷的边。

最大化 $\quad f(t, s)$
满足约束

$\begin{aligned} f(u, v) & \leq c(u, v), & (u, v) \in E \\ \sum_v f(u, v) & =\sum_v f(v, u), & u \in V \\ f(u, v) & \geq 0, & (u, v) \in E \cup\{(t, s)\} \end{aligned}$

最小费用流问题

最小化 $\quad \sum_{(u, v) \in E} f(u, v) w(u, v)$
满足约束

$\begin{array}{cr} f(u, v) \leq c(u, v), & (u, v) \in E \\ \sum_v f(u, v)-\sum_v f(v, u)=0, & u \in V-\{s, t\} \\ f(u, v) \geq 0, & (u, v) \in E \cup(t, s) \end{array}$

多物网络流问题

$\begin{array}{ll}\text { 最大化 } & 0\end{array}$
满足约束

$\begin{aligned} \sum_i f_i(u, v) & \leq c(u, v), & (u, v) \in E, i=1,2 \ldots, n \\ \sum_v f_i(u, v) & =\sum_v f_i(v, u), & u \in V, i=1,2, \ldots, n \\ f_i\left(t_i, s_i\right) & \geq d_i, & i=1,2, \ldots, n \\ f_i(u, v) & \geq 0, & (u, v) \in E \cup\left\{\left(t_i, s_i\right) \mid 1 \leq i \leq n\right\} \end{aligned}$

判断是否可行。

对偶问题

给定一个原始线性规划：
最小化 $\quad \sum_{j=1}^n c_j x_j$
满足约束 $\quad \sum_{j=1}^n a_{i j} x_j \geq b_i, \quad i=1,2, \ldots, m$

$x_j \geq 0, \quad j=1,2, \ldots, n$

定义它的对偶线性规划为:
最大化 $\quad \sum_{i=1}^m b_i y_i$
满足约束 $\quad \sum_{i=1}^m a_{i j} y_i \leq c_j, \quad j=1,2, \ldots, n$

$y_i \geq 0, \quad i=1,2, \ldots, m$

用矩阵可以更形象地表示为:
最小化 $\quad \mathbf{c}^T \mathbf{x} \quad$ 最大化 $\quad \mathbf{b}^T \mathbf{y}$
满足约束 $A \mathbf{x} \geq \mathbf{b}$ 互为对偶 满足约束 $A^T \mathbf{y} \leq \mathbf{c}$

$\mathbf{x} \geq 0 \quad \mathbf{y} \geq 0$

定理6.2. (线性规划对偶性) 若 $\mathbf{x}^*=\left(x_1^*, \ldots, x_n^*\right)$ 与 $\mathbf{y}^*=\left(y_1^*, \ldots, y_m^*\right)$ 分别是原问题 及对偶问题的最优解，那么

$\sum_{j=1}^n c_j x_j^*=\sum_{i=1}^m b_i y_i^*$

一个等式约束在对偶后得到一个无限制的变量。