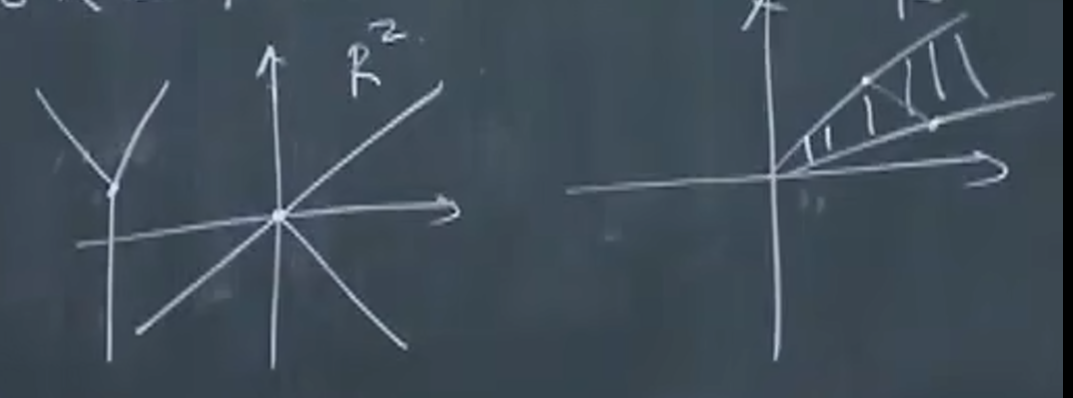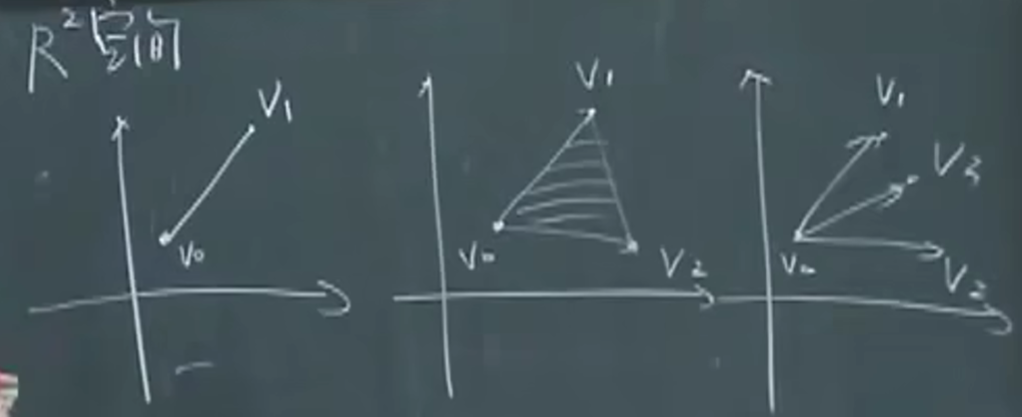仿射 affine
仿射集 Affine Sets
X1=X2∈Rn,θ∈R
直线
y=θX1+(1−θ)X2
线段
y=θX1+(1−θ)X2
限定 θ∈[0,1]。
仿射集:连接集合内任意两点的直线也在集合内。
Fancy定义:设 X1,⋯,Xk∈C,θ1,⋯,θk∈R,θ1+⋯+θk=1,放射组合:
θ1X1+⋯+θkXk∈C
定义等价?
(θ1+θ2)(θ1+θ2θ2X1+θ1+θ2θ2X2)+(1−θ1−θ2)X3
若要满足 αX1+βX2∈C,则需要过原点,或者观察到:
V=C−X0={X−X0∣X∈C}
这样 θ(X1−X0)+(1−θ)(X2−X0)=θX1+(1−θ)X2−X0∈V。
线性方程的解集是仿射集。
仿射包
affC={θ1X1+⋯+θkXk∣∀Xk∈C,∑θ=1}
凸性 convex
凸集
∀X1,X2∈C,∀θ,θ∈[0,1]
θX1+(1−θ)X2∈C
凸组合
∑θX,∑θ=1,θ∈[0,1]
凸包
convC={θ1X1+⋯+θkXk∣∀Xk∈C,∑θ=1,θ∈[0,1]}
锥 Cone
凸锥 Convex Cone
C 是锥 ⇔ ∀X∈C,θ≥0,有 θX∈C。
C 是凸锥 ⇔ ∀X1,X2∈C,θ1,θ2≥0,有 θ1X1+θ2X2∈C。
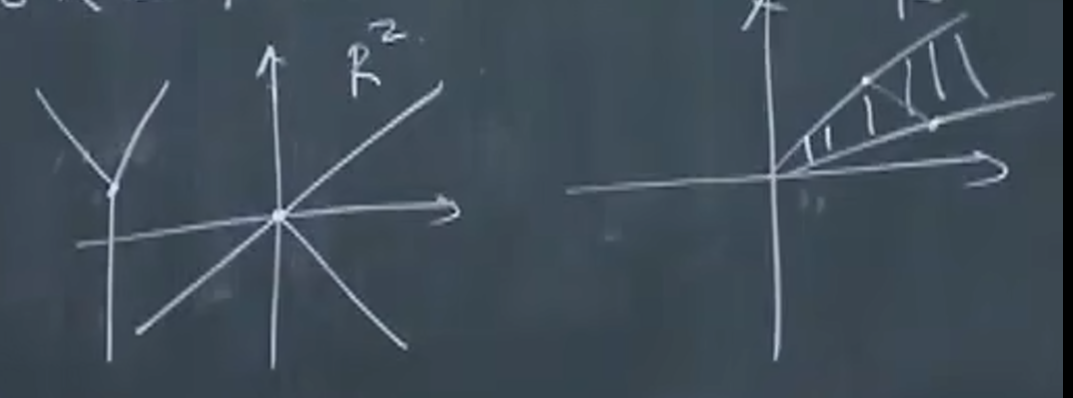
凸锥组合
∑θX,θ≥0
凸锥包
常见的凸集
超平面
{x∣aTx=b}
分成两部分:
αTx≥b,αTx≤b
半空间。
超平面和半空间都是凸集。
球和椭球
B(Xc,r)={x∣∣∣x−xc∣∣2=r}
是凸集
ε(XC,P)={x∣(X−XC)TP−1(X−XC)≤1}P∈S++n,XC∈Rn
奇异值对应半轴长的平方。
多面体
P={x∣ajTx≤bj,cjTx=dj}
有界多面体。
单纯形 Simplex
Rn 空间中选择 V0,⋯,Vk 共 k+1 个点。
V1−V0,⋯,Vk−V0
线性无关,则过点相关的单纯形为:
C=conv{V0,⋯,Vk}
{x∣x≤0}
取点 0,−∞,则构成了单纯形
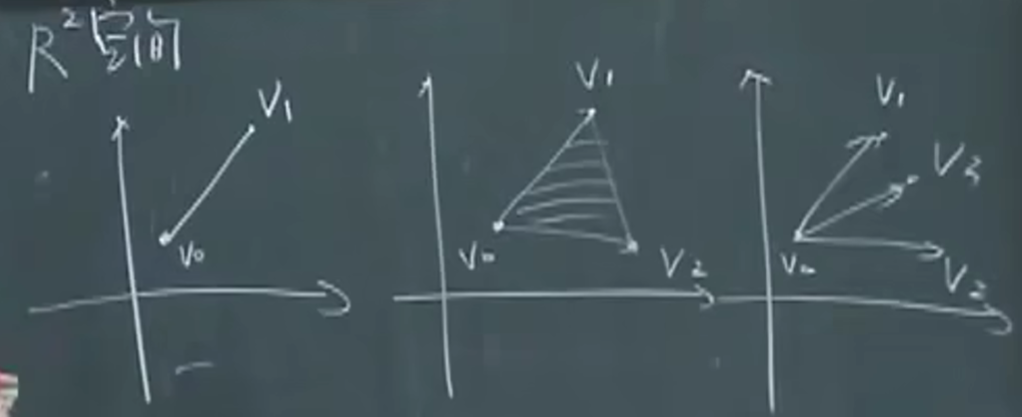
无法构造 V0,V1,V2,V3 单纯形。
一个单纯形一定是一个多面体。
在 n 维空间构造 Cn+1n=n+1 个超平面。
对称矩阵集合/对称半正定矩阵集合
Sn={X∈Rn×n∣X=XT}
S+n={X∈Rn×n∣X=XT,X⪰0}
S++n={X∈Rn×n∣X=XT,X≻0}
证明 S+n 是凸锥。可以说明 θA 是半正定矩阵,θ1A+θ2B 是半正定。
但是 S++n 不是凸锥,因为当 θ=0 就不是正定。

保凸操作
任意多个凸集的交集是凸集
若 S1,S2 为凸,则 S1∩S2 为凸。
若 Sa 为凸集 ∀a∈A,则 ∩a∈ASa 为凸集。
仿射函数是保凸函数
f:Rn→Rm 是放射的,f(x)=Ax+b。
A∈Rm×n,b∈Rm。
若 S∈Rn 为凸,f:Rn→Rm 放射,则
f(S)={f(x)∣x∈S}
也是凸集。
几何意义是拉伸和旋转。
缩放和移位是保持凸性的。
两个凸集的和是凸的
S1+S2={x+y∣x∈S1,y∈S2}
S1×S2={(x,y)∣x∈S1,y∈S2}
笛卡尔积。
S1 与 S2 是凸集可以推出 S1×S2 是凸集,然后根据仿射函数保凸,则 S1+S2 是凸集。
类似的证明:r(A)+r(B)≥r(A∣B)≥r(A+B)。
线性不等式的解集是凸的
根据一个线性不等式的解集是一个超平面,是凸的,取交集之后还是凸的证明。
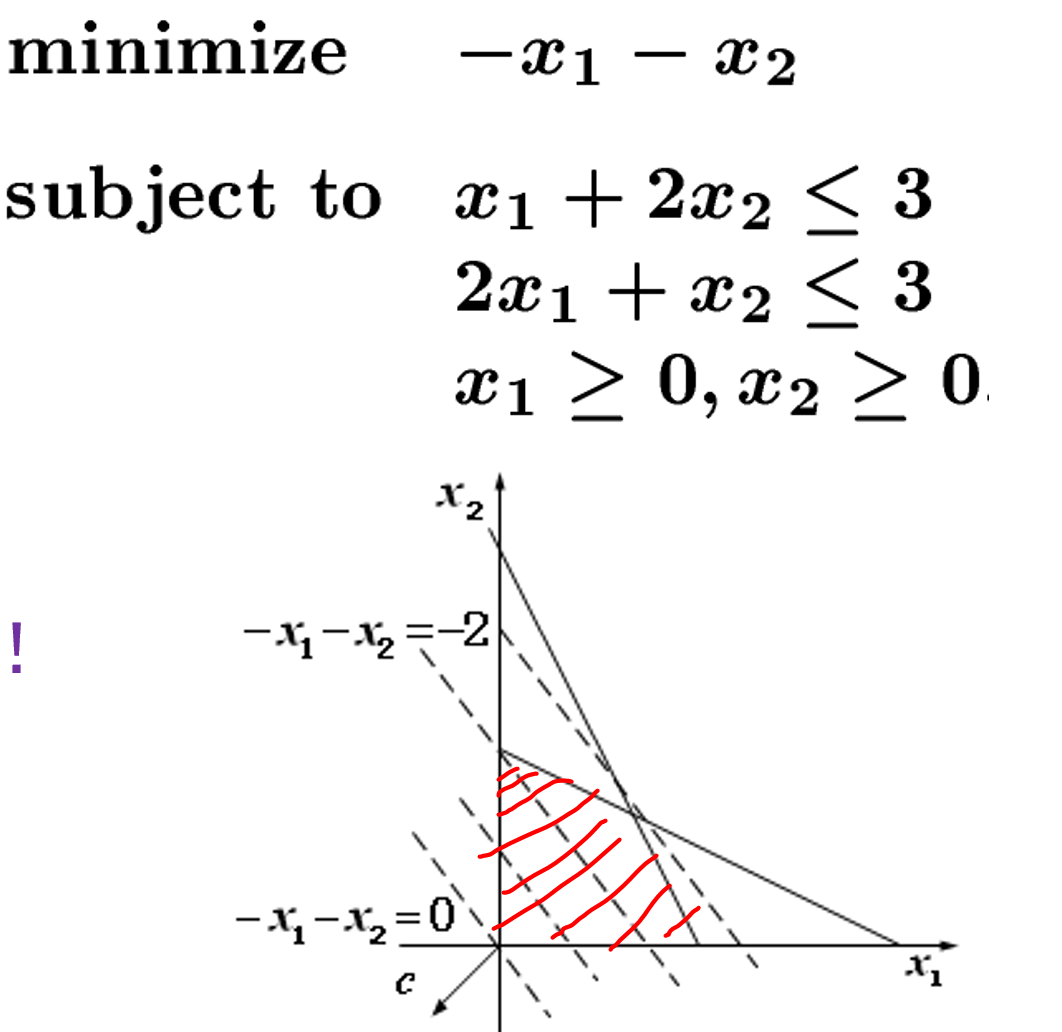
如图,线性不等式的解集由红色区域表示。
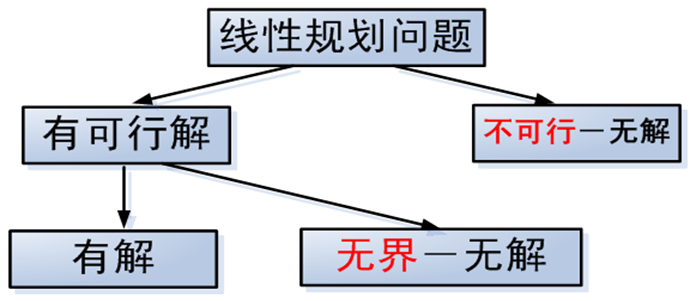
线性规划解的几何特征:
- 有解:惟一解或多个解(整条边、面、甚至整个可行集)
- 无界:没有有限最优解
- 不可行:没有可行解,题目所给条件矛盾
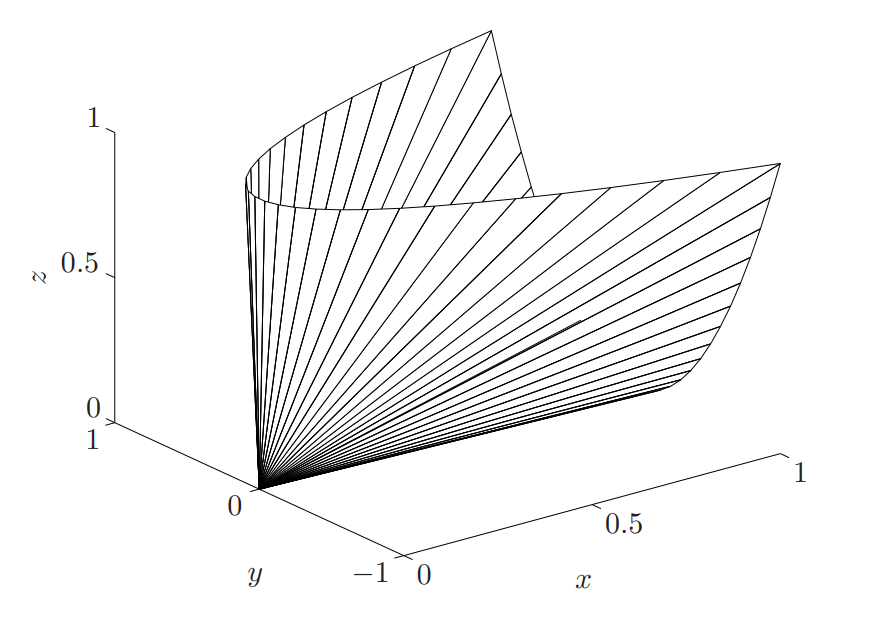
极点 extreme point
几何上:极点即不能位于连接该集合中其它两点的开线段上的点
定义:称凸集中的点 x 是 C 的极点,如果存在 C 中的点 y,z 和某 θ∈(0,1),有:
x=θy+(1−θ)z
则必有 y=z。
令 C={x∈Rn:Ax=b,x≥0},则 x 是 C 的极点当且仅当 x 是系统 Ax=b,x≥0 的基本可行解。
若线性规划有解,则必有一个极点是最优解。
如果最优解都不是极点则能找到 y=z,使得 x=θy+(1−θ)z,但是这样 y,z 中必有一个更优。
线性矩阵不等式 LMI
A(X)=X1A1+⋯+XnAn⪯B
B,Ai,Xi∈Sm
{X∣A(X)⪯B}
为凸集。
定义仿射变换 f(x)=B−A(X) 一系列对称矩阵 X1,⋯,Xn 到 一个矩阵。
而 S+n 为凸。则仿射变换后也为凸。
透视函数 Perspective Function
P:Rn+1→Rn
domP=Rn×R++
最后一个元素是正数
P(z,t)=tz
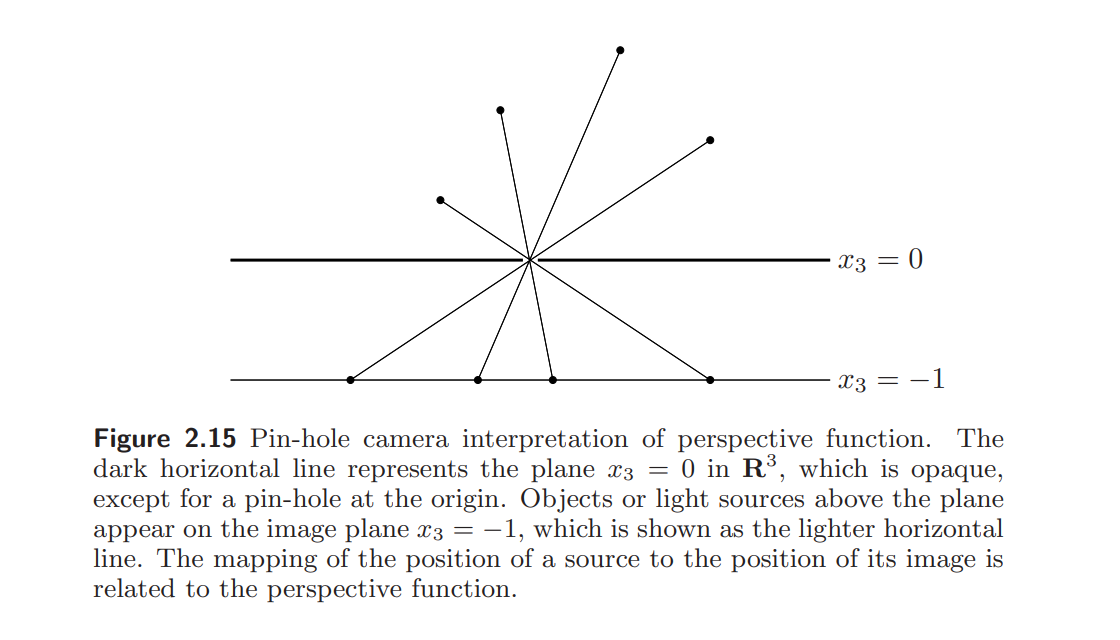
透视函数是保凸函数
Suppose that x=(x~,xn+1),y=(y~,yn+1)∈Rn+1 with xn+1>0, yn+1>0. Then for 0≤θ≤1, 考虑凸组合 θx+(1−θ)y
P(θx+(1−θ)y)=θxn+1+(1−θ)yn+1θx~+(1−θ)y~=μP(x)+(1−μ)P(y),
where
μ=θxn+1+(1−θ)yn+1θxn+1∈[0,1].
P(x)=xn+1x~,Q(x)=yn+1y~
This correspondence between θ and μ is monotonic: as θ varies between 0 and 1 (which sweeps out the line segment [x,y] ), μ varies between 0 and 1 (which sweeps out the line segment [P(x),P(y)]). This shows that P([x,y])=[P(x),P(y)].
逆函数 P−1(C)={(x,t)∈Rn+1∣x/t∈C,t>0} 也是保凸函数,映射为一个凸锥。
我们这里讲的逆函数将值域中的每个点映射到可以生成这个点的所有定义域中的点。
线性分数函数 Linear-fractional functions
g(x)=[AcT]x+[bd]A∈Rm×nc∈Rnb∈Rmd∈R
两个随机变量的联合概率
Example 2.13 Conditional probabilities. Suppose u and v are random variables that take on values in {1,…,n} and {1,…,m}, respectively, and let pij denote prob(u=i,v=j). Then the conditional probability fij=prob(u=i∣v=j) is given by
fij=∑k=1npkjpij.
Thus f is obtained by a linear-fractional mapping from p.
It follows that if C is a convex set of joint probabilities for (u,v), then the associated set of conditional probabilities of u given v is also convex.