Manacher算法

1 约定

字符的非空有限集，称为字母表 (alphabet)。
字母表中字符的有限序列，称为字符串 (string)。
字符串中字符的个数，称为该字符串的长度 (length)。
字符串中连续的一段，称为该字符串的子串 (substring)。
字符串中反转后与反转前相同的子串，称为该字符串的回文子串 (palindromic substring)。
字符串中长度最大的回文子串，称为该字符串的最长回文子串 (longest palindromic substring)。
以字符串第 $i$ 位为中心的回文子串的最大长度的一半，称为该字符串第 $i$ 位的回文半径 (radius of palindrome)，记为 $R[i]$ 。
一般来说，字符串 $s$ 长度约定为 $n$ 。
$s[l..r]$ 表示 $s$ 的第 $l$ 位到第 $r$ 位的字符组成的子串。
$s[p]$ 表示 $s$ 第 $p$ 位的字符。
$rev(s)$ 表示字符串 $s$ 的反转。
$a+b$ 表示两个字符串 $a,b$ 按顺序拼接形成的字符串。
$suf(s,i)$ 代表字符串 $s[i..n]$ 。
$pre(s,i)$ 代表字符串 $s[1..i]$ 。
我们记 $Lb(i)=i+R[i]-1,Rb(i)=i-R[i]+1$ ，即以 $i$ 这个位置为中心的最长回文串的左端点和右端点。

2 回文子串问题和经典解法

问题简述

找到一个字符串 $s$ 的最长回文子串。

问题转化

为了避免奇偶讨论和边界问题，从而降低代码复杂度，我们在字符串每一位两侧都添加同一个特殊字符，然后在字符串首位添加不同的特殊字符，末尾再添加一个不同的特殊字符。

比如说我们通过这样的变换，将 $\texttt{ababcba}$ 变成。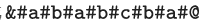

这样我们只用求长度为奇数的回文串了，而且假设求出来的最长回文半径为 $Rmax$ ，答案就是 $Rmax-1$ ，可以自己简单证明一下。

其他算法

$暴力 \mathcal O(n^2)$

先固定回文串的中心 $i$ ，然后维护指针 $p$ ，暴力向两边扩展，即 $p=p+1$ ，当 $s[i+p] \not= s[i-p]$ 或者越界的时候，停止扩展。

后缀数组 $\mathcal O(n \log n)$

根据我们的暴力做法， $R[i]$ 等于 $s[i..n]$ 和反转后的 $s[1..i]$ 的 $\text{LCP}$ （最长公共前缀）。

我们构造 $s'=s+\texttt{}+rev(s)$ ，那么 $\text{LCP}(s[i..n],s[1..i])$ 可以转化为 $\text{LCP}(suf(s',i),suf(s',2 \times n-i+1))$ 。通过 Height 数组上二分 + ST 表预处理，我们可以 $\mathcal O (\log n)$ 算出任意两个 $s'$ 的后缀之间的 $\text{LCP}$ ，这样可以做到 $\mathcal O(n \log n)$ 。

哈希 $\mathcal O(n \log n)$

可以观察到，对于位置 $i$ ，若半径取 $r$ 时，可以构成回文串，那么对于 $\forall r' \le r$ ，也可以构成回文串。

那么就具有单调性，可以预处理出 $s$ 和 $rev(s)$ 的哈希值，然后二分解决。

Manacher 算法

基本做法

维护变量 $i$ ，从左到右一直扫到 $n$ 。

我们记录两个辅助变量 $mx$ 和 $p$ ，分别表示已有回文串覆盖到的最右边界，和对应的中心。

就是 $\max \lbrace Rb(k), k \in [1,i-1] \rbrace$ 和其对应的 $k$ 。

现在我们的任务就是计算出 $R[i]$ 。

我们可以想到，先给 $R[i]$ 一个下界，然后后面再扩展 $R[i]$ 直至 $R[i]$ 再增加，这个串不是回文串。

如何寻找这个下界呢，我们需要利用我们已知的 $R[k],k \in [1,i-1]$ 。

我们记 $j=p \times 2 -i$ ，代表 $i$ 关于 $p$ 的对称点，为什么要找这个点呢，等下来慢慢讲。

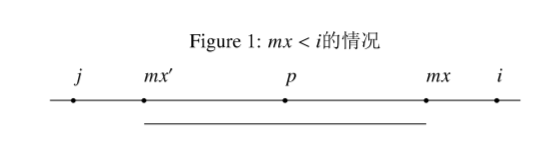
当 $mx < i$ ，等于我们对前面的情况一无所知，所以我们只能将 $R[i]$ 设成 1。
当 $mx-i>R[j]$ 。

我们来推一下 $j$ 这个点有什么性质，首先 $rev(s[Lb(j)..j])=s[j..Rb(j)] ..(1)$ 。

又因为 $j$ 是 $i$ 关于 $p$ 的对称点，那么 $rev(s[i..i+R[j]-1])=s[Lb(j)..j]..(2)$ 且 $rev(s[i..i-R[j]+1])=s[j..Rb(j)]..(3)$ 。

而我们有性质 $rev(s)=rev(t) \Leftrightarrow s=t$ ，那么我们把 $(1)$ 代入 $(2),(3)$ 两式，得到 $rev(s[i..i+R[j]-1]=rev(s[i..i-R[j]+1])$ ，得到 $s[i..i+R[j]-1]=s[i..i-R[j]+1]$ ，那么就发现 $R[i]$ 的下界就是 $R[j]$ 。
当 $mx-i \le R[j]$ ，就比较遗憾，发现 $i+R[j]-1 > mx$ ，这时我们的 $R[j]$ 下界只能取到 $mx-i$ 。

代码实现

#include <bits/stdc++.h>
#define MAXN 600005
using namespace std;
inline int read(){
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-') f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		x=x*10+ch-'0';
		ch=getchar();
	}
	return x*f;
}
char s[MAXN],t[MAXN];
int tot;
void Init(){
	int len=strlen(s+1);
	t[++tot]='&';
	for (int i=1;i<=len;++i) t[++tot]='#',t[++tot]=s[i];
	t[++tot]='#',t[++tot]='@';
}
int R[MAXN];
void Manacher(){
	int mx=0,j=0;
	for (int i=1;i<=tot;++i){
		R[i]=mx>i?min(mx-i,R[2*j-i]):1;
		while (t[i-R[i]]==t[i+R[i]]) R[i]++;
		if (R[i]+i>mx) mx=R[i]+i,j=i;
	}
}
int main(){
	scanf("%s",s+1);
	Init(),Manacher();
	int ans=0;
	for (int i=1;i<=tot;++i) ans=max(ans,R[i]);
	printf("%d\n",ans-1);
	return 0;
}

时间复杂度分析

如果我们能用不超过 $\mathcal O(\Delta)$ 的时间复杂度使 $mx$ 向后移动 $\Delta$ ，那么我们的算法是 $\mathcal O(n)$ 的。

对于情况 1，我们用 $\mathcal O(x)$ 的代价，就可以让 $mx$ 移动 $i-mx'+x$ ，其中 $mx'$ 代表这次移动前的 $mx$ ， $i-mx'$ 为正数。

因为 $s[Lb(j)-1] \not= s[Rb(j)+1]$ ，所以上述的情况 2 $R[i]$ 不会增加，相应地 $mx$ 自然不会移动。

对于情况 3，我们用 $\mathcal O(x)$ 的代价，可以让 $mx$ 移动 $x$ 。

综上，我们的算法是 $\mathcal O(n)$ 的。

一个小结论

任意一个字符串本质不同的回文字串的个数 $S$ 是 $\mathcal O(n)$ 的。

这个可以通过类似上述时间复杂度分析的方法得出。

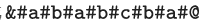我们发现 $R[i]$ 每自增一次， $S$ 最多增加 1，而 $R[i]$ 自增的次数是 $\mathcal O(n)$ 的，那么意味着 $S$ 是 $\mathcal O(n)$ 的。