运动学

基本概念

参考系

用来描述物体运动而选作参考的物体、或相对静止的物体系。运动的相对性决定描述物体运动必须选取参考系。

• 太阳参考系
• 地心参考系
• 地面参考系
• 质心参考系

坐标系

坐标系为参考系的数学抽象。由固结在参考系上的一组有刻度的射线、曲线或角度表示。坐标系可任选，以描述方便为原则。

• 直角坐标系 $(x,y,z)$
• 球坐标系 $(r,\theta,\varphi)$
• 柱坐标系 $(\rho,\theta,z)$
• 自然坐标系

质点位置、速度、加速度的描述

质点：物体的大小、形状可以忽略；运动过程中，物体的各部分运动相同。

平均速度：

$\overline{\boldsymbol{v}}=\frac{\Delta \boldsymbol{r}}{\Delta t}$

瞬时速度：

$\boldsymbol{v}=\lim_{\Delta t \to 0}\frac{\Delta \boldsymbol{r}}{\Delta t}=\frac{\mathrm{d} \boldsymbol{r}}{\mathrm{d} t}$

速度大小与速率相等，怎么证明？利用 $\lim_{\Delta t \to 0} \Delta s=\lim_{\Delta t \to 0} |\Delta \boldsymbol{r}|$。

直角坐标系

位矢

$\boldsymbol{r} = x \boldsymbol i+y \boldsymbol{j}+z\boldsymbol{k}$

经常考参数方程参数的消去，得到 $x,y,z$ 满足的方程。

速度

$\begin{gathered} \vec{v}=\frac{\mathrm{d} \vec{r}}{\mathrm{~d} t}=\frac{\mathrm{d} x}{\mathrm{~d} t} \vec{i}+\frac{\mathrm{d} y}{\mathrm{~d} t} \vec{j}+\frac{\mathrm{d} z}{\mathrm{~d} t} \vec{k} \\ \vec{v}=v_x \vec{i}+v_y \vec{j}+v_z \vec{k} \\ \Rightarrow v_x=\frac{\mathrm{d} x}{\mathrm{~d} t}, \text { etc. } \quad \int_{t_A}^{t_B} v_x \mathrm{~d} t=\int_{t_A}^{t_B} \frac{\mathrm{d} x}{\mathrm{~d} t} \mathrm{~d} t=\int_{x_A}^{x_B} \mathrm{~d} x \\ =x_B-x_A \end{gathered}$

速率: $\quad v=|\vec{v}|=\sqrt{v_x^2+v_y^2+v_z^2}$

代表对每个分量进行分析。

加速度

加速度的表达形式：

$\boldsymbol a=\frac{\mathrm d \boldsymbol v}{\mathrm d t}=\frac{\mathrm d^2 \boldsymbol r}{\mathrm d t^2}$

转换技巧（如果只考虑一维）：

$\boldsymbol a=\frac{\mathrm d \boldsymbol v}{\mathrm d x} \frac{\mathrm d x}{\mathrm d t}=\frac{\mathrm d \boldsymbol v}{\mathrm d x}\boldsymbol v=\frac{\mathrm d (\frac{1}{2}\boldsymbol v^2)}{\mathrm d x}$

这样，知道 $\boldsymbol a$ 和 $\boldsymbol x$ 的关系，也可以推出 $\boldsymbol v$ 的方程。例如：

跳水运动员自 $10 \mathrm{~m}$ 跳台自由下落, 入水后因受水的阻碍而减速, 设加速度 $a=-k v^2$, $k=0.4 \mathrm{~m}^{-1}$. 求运动员速度减为入水速度 $10 \%$ 时的入水深度.

解: 取坚直向下为 $x$ 轴, $a=-k v^2=\frac{\mathrm{d} v}{\mathrm{~d} x} \frac{\mathrm{d} x}{\mathrm{~d} t}=v \frac{\mathrm{d} v}{\mathrm{~d} x}$, 所以 $x=\frac{1}{k} \ln \frac{v_0}{v}$. 将 $v=0.1 v_0$ 代入, 解得$x=\frac{1}{k} \ln 10=5.76 \mathrm{~m}$.

分离变量的做法：

$a_x\mathrm d x=v_x\mathrm d v_x$

积分得到

$a_x(x)=v_x(x)=\frac{\mathrm dx}{\mathrm d t}$

继续积分，得到

$\int \mathrm d t=\int \frac{\mathrm d x}{v_x(x)}$

因此，可以得到 $t$ 与 $x$ 的关系。

$\begin{aligned} \vec{a}=\frac{\mathrm{d} \vec{v}}{\mathrm{~d} t} & =\frac{\mathrm{d} v_x}{\mathrm{~d} t} \vec{i}+\frac{\mathrm{d} v_y}{\mathrm{~d} t} \vec{j}+\frac{\mathrm{d} v_z}{\mathrm{~d} t} \vec{k} \\ & =\frac{\mathrm{d}^2 x}{\mathrm{~d} t^2} \vec{i}+\frac{\mathrm{d}^2 y}{\mathrm{~d} t^2} \vec{j}+\frac{\mathrm{d}^2 z}{\mathrm{~d} t^2} \vec{k} \\ & =a_x \vec{i}+a_y \vec{j}+a_z \vec{k} \\ \Rightarrow a_x & =\boxed{\frac{\mathrm{d} v_x}{\mathrm{~d} t}=\frac{\mathrm{d}^2 x}{\mathrm{~d} t^2}}, \text { etc. } \end{aligned}$

**自然坐标系

速度

考虑某一个点的运动，会出现切向 $\boldsymbol \tau$ 和法向 $\boldsymbol n$。切向指向某点的运动方向。

$\boldsymbol v= \boldsymbol v_\tau=v\cdot \boldsymbol e_\tau$

加速度

$\boldsymbol a=\boldsymbol a_n+\boldsymbol a_\tau$

其中

$a_n=\frac{v^2}{\rho} \quad \boxed{\rho=\frac{(1+y'^2)^{3/2}}{|y''|}}$

$a_\tau=\frac{\mathrm d v}{\mathrm d t}$

推导：

$\boldsymbol a=\frac{\mathrm d (\boxed{\boldsymbol e_tv})}{\mathrm d t}=\frac{\mathrm d v}{\mathrm d t}\boldsymbol e_t+\frac{\mathrm d \boldsymbol e_t}{\mathrm d t}v=\frac{\mathrm d v}{\mathrm d t}\boldsymbol e_t+v\frac{\mathrm d \theta}{\mathrm d t}\boldsymbol e_n$

注意两个单位向量之间的关系。$\frac{\mathrm d \boldsymbol e_t}{\mathrm d t}=\frac{\mathrm d \theta}{\mathrm d t}\boldsymbol e_n$。

对后面一项进一步变形，很多情况，曲线运动的时候我们不知道角速度 $\frac{\mathrm d \theta}{\mathrm d t}$ 是什么，因此需要进一步推导：

$\frac{\mathrm d \theta}{\mathrm d t}=\frac{\mathrm d \theta}{\mathrm d s}\frac{\mathrm d s}{\mathrm d t}$

后面一项为速度，前一项只与曲线的形状有关。

定义 曲率：

$k=\frac{\mathrm d \theta}{\mathrm d s}=\lim_{\Delta t \to 0} \frac{\Delta \theta}{\Delta s}$

定义 曲率半径：

$\rho=\frac{1}{k}$

推出，$\frac{\mathrm d \theta}{\mathrm d t}=\frac{\mathrm d \theta}{\mathrm d s}\frac{\mathrm d s}{\mathrm d t}=\frac{v}{\rho}$，

$\boldsymbol a=\frac{\mathrm d v}{\mathrm d t}\boldsymbol e_t+v\frac{\mathrm d \theta}{\mathrm d t}\boldsymbol e_n=\boxed{\frac{\mathrm d v}{\mathrm d t}\boldsymbol e_t+\frac{v^2}{\rho}\boldsymbol e_n}$

其中，

$\boldsymbol a_t= \frac{\mathrm d v}{\mathrm d t}=\frac{\mathrm d^2s}{\mathrm d t^2}$

反应速度大小的变化，朝向切向。

$\boldsymbol a_n=\frac{v^2}{\rho}$

反应速度方向的变化。

圆周运动（自然坐标系）

此时，曲率半径 $\rho=R$，得到，

$\boldsymbol a=R\beta \boldsymbol{e}_t+R\omega^2 \boldsymbol e_n$

$\boldsymbol a_t= \frac{\mathrm d v}{\mathrm d t}=\frac{\mathrm d (R\omega)}{\mathrm d t} =R\beta$

$\boldsymbol a_n=\frac{v^2}{\rho}=R\omega^2$

角速度、角加速度。

注意，$\boldsymbol a_t = 0$ 不意味着加速度为 $0$，还要考虑 $\boldsymbol a_n$。匀速圆周运动 $\beta=0$。

**极坐标系

位置

$\boldsymbol{e}_r$：径向单位矢量（沿着 $\boldsymbol{r}$）

$\boldsymbol{e}_\theta$：横向单位矢量（和 $\boldsymbol{r}$ 垂直）

位置矢量的表示：

$\boldsymbol{r}=r\boldsymbol{e}_r\\ \boldsymbol{r}=\boldsymbol{r}(t)={r}(t)\boldsymbol{e}_r(t)$

两个量都随着时间变化（两个自由度）

速度

$\boldsymbol v=\frac{\mathrm d (\boldsymbol e_rr)}{\mathrm d t}=\frac{\mathrm d r}{\mathrm d t} \boldsymbol e_r+r\frac{\mathrm d\theta}{\mathrm dt} \boldsymbol e_\theta$

径向速度：

$v_r=\frac{\mathrm d r}{\mathrm d t}$

横向速度：

$v_\theta=r\frac{\mathrm d \theta}{\mathrm d t}=r\omega$

加速度

$\boldsymbol e_r$ 径向方向。$\boldsymbol e_\theta$ 横向方向。

回顾：

$\boldsymbol v=\frac{\mathrm d r}{\mathrm d t} \boldsymbol e_r+r\frac{\mathrm d\theta}{\mathrm dt} \boldsymbol e_\theta$

第一项求导：

$\frac{\mathrm d ^2 r}{\mathrm d t^2} \boldsymbol e_r+\frac{\mathrm d r}{\mathrm d t} \frac{\mathrm d \boldsymbol e_r}{\mathrm d t}$

而 $\frac{\mathrm d \boldsymbol e_r}{\mathrm d t}$ 代表径向方向的变化，得到：

$\frac{\mathrm d \boldsymbol e_r}{\mathrm d t}=\frac{\mathrm d \theta}{\mathrm d t}\boldsymbol e_\theta$

第二项求导：

$\frac{\mathrm d r}{\mathrm d t}\frac{\mathrm d\theta}{\mathrm dt} \boldsymbol e_\theta+r\frac{\mathrm d^2 \theta}{\mathrm d t^2}\boldsymbol e_\theta+ r\frac{\mathrm d \theta}{\mathrm d t} \frac{\mathrm d \boldsymbol e_\theta}{\mathrm d t}$

而 $\frac{\mathrm d \boldsymbol e_\theta}{\mathrm d t}$ 代表横向方向的变化，得到：

$\frac{\mathrm d \boldsymbol e_\theta}{\mathrm d t}=-\frac{\mathrm d \theta}{\mathrm d t}\boldsymbol e_r$

而方向相反，因为是指向中心的。

因此：

$a_r=\frac{\mathrm d^2 r}{\mathrm d t^2} - r \left( \frac{\mathrm d \theta}{\mathrm d t}\right)^2=\ddot{r}-r\omega^2$

$a_\theta=r \frac{\mathrm d ^2 \theta}{\mathrm d t^2} + 2 \frac{\mathrm d r}{\mathrm d t} \frac{\mathrm d \theta}{\mathrm d t}=r\ddot{\theta}+2\dot{r} \omega$

运动方程与轨道

$\boldsymbol r=\boldsymbol r(t) \quad \boldsymbol r(t)=x(t)\boldsymbol i+y(t)\boldsymbol j+z(t)\boldsymbol k$

分量形式：

$\left\{ \begin{aligned} x=x(t)\\ y=y(t)\\ z=z(t)\\ \end{aligned} \right.$

消掉时间参量，如

$\left\{ \begin{aligned} x=r\cos\omega t\\ y=r\sin\omega t \end{aligned} \right.$

得到

$x^2+y^2=r^2$

得到了运动的轨道（方程）


位移

$\Delta \boldsymbol{r}=\boldsymbol{r}_B-\boldsymbol{r}_A\\ \Delta \boldsymbol{r}=\Delta x \boldsymbol{i}+\Delta y \boldsymbol{j}+\Delta z \boldsymbol{k}$

位移具有 矢量叠加性质。

位移与路程 $\Delta s$ 不同。

• 位移为矢量，路程为标量
• $\Delta s \not=|\Delta \boldsymbol{r}|$ 只有当 $\Delta t \to 0$ 时。

$\begin{gathered} \int_{\widehat{A B}} \mathrm{d} s=\int_{\widehat{A B}}|\mathrm{d} \vec{r}| \\ \int_{\widehat{A B}} \mathrm{d} \vec{r}=\vec r_B-\vec r_A=\Delta \vec{r} \\ \int_{\widehat{A B}} \mathrm{d} r=\int_{\widehat{A B}} \mathrm{d}|\vec{r}|=|r_B|-|r_A|=\Delta r \end{gathered}$

1. 表现了 $\Delta s \not=|\Delta \boldsymbol{r}|$ 只有当 $\Delta t \to 0$ 时。
2. 矢量首尾相连。
3. 路程的变化量相加。$\Delta r=|\boldsymbol{r}_B|-|\boldsymbol{r}_A|$

在实际算路程的过程中，利用 $(1)$ 式，我们分别计算位移朝向相同的部分，以速度为 0 的点为分段点，取绝对值加起来即为路程。例如：

有一质点沿 $x$ 轴做直线运动, $t$ 时刻的坐标为 $x=4.5 t^2-2 t^3$. 试求:
(1) 第 2 秒内的平均速度;
(2) 第 2 秒末的瞬时速度;
(3) 第 2 秒内的路程.
解:
(1) 平均速度 $\bar{v}=\frac{x_{(t=2)}-x_{(t=1)}}{\Delta t}=\frac{2-2.5}{1}=-0.5 \mathrm{~m} / \mathrm{s}$.
(2) 第 2 秒末的瞬时速度 $v=\left.\frac{\mathrm{d} x}{\mathrm{~d} t}\right|_{t=2}=\left.\left(9 t-6 t^2\right)\right|_{t=2}=-6 \mathrm{~m} / \mathrm{s}$.
(3) 当速度为 0 时, 即 $9 t-6 t^2=0$, 解得 $t_1=0 \mathrm{~s}, t_2=1.5 \mathrm{~s}$, 以 $1.5 \mathrm{~s}$ 作为分段点, 路程 $s=\left|x_{(t=1.5)}-x_{(t=1)}\right|+\left|x_{(t=1.5)}-x_{(t=2)}\right|=\left|\frac{27}{8}-\frac{5}{2}\right|+\left|\frac{27}{8}-2\right|=2.25 \mathrm{~m}$.

相对运动

是对位置矢量描述的相对性。

$\boldsymbol r=\boldsymbol r'+\boldsymbol R$

其中 $\boldsymbol R$ 是从 $S$ 坐标系原点到 $S'$ 坐标系原点的位置矢量。即 $S'$ 原点在 $S$ 坐标系中的位置矢量。是空间测量的绝对性。

但是在 $S$ 坐标系和 $S'$ 坐标系中的测量可能不一样，例如时间、空间。设 $S'$ 时间是 $t'$。如果能够保证 $\Delta t=\Delta t'$

$\mathrm d t=\Delta t_{\Delta t\to 0}\\ \frac{\mathrm d \boldsymbol r}{\mathrm d t}=\frac{\mathrm d \boldsymbol R}{\mathrm d t}+\frac{\mathrm d \boldsymbol r'}{\mathrm d t}=\frac{\mathrm d \boldsymbol R}{\mathrm d t}+\frac{\mathrm d \boldsymbol r'}{\mathrm d t'}\\ \boldsymbol v=\boldsymbol v'+\boldsymbol u\\ \boldsymbol a=\boldsymbol a'+\frac{\mathrm d \boldsymbol u}{\mathrm d t}$

$\boldsymbol u$ 牵连速度，$\mathrm d \boldsymbol u/\mathrm d t$ 牵连加速度。绝对=相对+牵连。

$\left\{ \begin{matrix}x=x'+ut\\y=y'\\z=z'\\t=t'\end{matrix}\right.$

参考系的转动

综合例题

描述质点运动的物理量有位矢、位移、速度和加速度等，而质点在某时刻的运动状态主要由位置和速度所确定，因此通常所说质点运动状态指的是它的位矢和速度确定的状况。

常见的解题方法

1. 套公式、求导。明确每个物理量的含义。
2. 用相对牵连关系或者运动的合成分解。

加速度、速度的求法

• 根据数学表达式进行计算。
• 进行分解。

$\boldsymbol r=\boldsymbol r_0+\int_{t_0}^t \boldsymbol v \mathrm d t$

$\boldsymbol v=\boldsymbol v_0+\int_{t_0}^t \boldsymbol a \mathrm d t$

初值问题。

路程的求法

本质上是高数的曲线求和。

$\int_{s_0}^s \mathrm d s=\int_{s_0}^s \sqrt{(\mathrm d x)^2+(\mathrm d y)^2}\\=\int_{s_0}^s \sqrt{1+\left(\frac{\mathrm d x}{\mathrm d y}\right)^2}\mathrm d y$

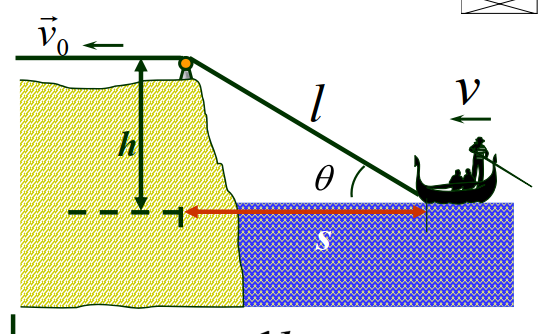
速度：

几何关系：

$l^2=h^2+s^2$

对时间进行求导，得

$2\frac{\mathrm d l}{\mathrm d t}l=2 \frac{\mathrm d s}{\mathrm d t}s$

由于 $v=-\mathrm d s/\mathrm d t,v_0=-\mathrm d l/\mathrm d t$，可以发现

$v_0l=vs,v=\frac{l}{s}v_0$

也可以将 $v$ 分解为沿绳方向和垂直绳方向。得到 $v \cos \theta=v_0,v=\frac{v_0}{\cos \theta}$。

加速度：

可以使用第一个表达式：

$a=\frac{\mathrm d v}{\mathrm d t}=v_0\left(\frac{s\mathrm d l-l\mathrm d s}{s^2\mathrm d t} \right)=v_0\left(-\frac{1}{s}v_0+\frac{l}{s^2} v \right)\\=v_0\left(-\frac{1}{s}v_0+\frac{l^2}{s^3} v_0\right)=v_0^2 \frac{h^2}{s^3}$

也可以使用带角度的表达式：

$\begin{aligned} a&=v_0\frac{\mathrm d \frac{1}{\cos \theta}}{\mathrm d t}\\&=v_0\frac{-1}{\cos^2 \theta}(-\sin\theta)\frac{\mathrm d \theta}{\mathrm d t} \end{aligned}$

切向速度为 $v \sin \theta$，半径为 $l$，$\frac{\mathrm d \theta}{\mathrm d t}$ 可以使用 $v\sin\theta/l$ 计算，因此：

$a=\frac{v_0^2h^2}{s^3}$

用相对运动的观点。

$\boldsymbol v=\boldsymbol v_r+\boldsymbol v_\theta$

得到

$v\cos\theta=v_r \Rightarrow v=\frac{v_r}{\cos\theta}=\frac{v_0}{\cos\theta}=\frac{lv_0}{s}$

$\boldsymbol a=\boldsymbol a_r+\boldsymbol a_\theta$

$a_r=\ddot{r}-r\omega^2=0-r\left(\frac{v_\theta}{l}\right)^2=\frac{h^2}{s^2l}$

$a\cos\theta=a_r\Rightarrow a=\frac{a_r}{\cos\theta}=\frac{v_0^2 h^2}{s^3}$


利用相对运动。在圆柱面上看，$P$ 的方向沿切向，因此

$\boldsymbol v_p=\boldsymbol v'+\boldsymbol v$

得到

$v_p=v\tan\theta \quad v'=v/\cos\theta$

要求出 $a_p$ 需要对 $v_p$ 求导：

$a_p=a\tan\theta+v\frac{\mathrm d \tan \theta}{\mathrm d \theta}\frac{\mathrm d \theta}{\mathrm d t}=a\tan\theta + v\sec^2 \theta \left(-\frac{v}{R\cos\theta}\right)$

直观上来说，$\theta$ 应该是减小的，所以 $\mathrm d \theta/\mathrm d t$ 应该取负值。

或者，利用相对运动，在圆柱面上看，$P$ 的速度方向沿切向，加速度方向有沿着切向和沿着法向的，设为 $\boldsymbol a_\tau,\boldsymbol a_n$，在地面上看，应该是两者加速度的叠加

$\boldsymbol a_P=\boldsymbol a_\tau+\boldsymbol a_n+\boldsymbol a$

然后投影即可。


一质点在平面直角坐标系内运动，在位置 $(x,y)$ 处的速度 $\boldsymbol v=v_x \boldsymbol i+v_y \boldsymbol j$，加速度 $\boldsymbol a=a_x\boldsymbol i+a_y \boldsymbol j$。

$v^2=v_x ^2+v_y^2$

$\boldsymbol a_t$ 为 $a_x \boldsymbol i$ 在其方向上的投影与 $a_y\boldsymbol j$ 在其方向上的投影之和。

$|\boldsymbol a_t|= a_x \frac{v_x}{v}+a_y \frac{v_y}{v}$

由 $a^2=a_t^2+a_n^2=a_x^2+a_y^2$（选取的坐标系不同）

得到

$|\boldsymbol a_n|=\left|\frac{a_xv_y-a_yv_x}{v}\right|$

事实上：

$\begin{bmatrix}a_t\\a_n\end{bmatrix}=\begin{bmatrix}\cos \theta & \sin \theta \\-\sin\theta &\cos \theta \end{bmatrix}\begin{bmatrix}a_x\\a_y\end{bmatrix}$

其中 $\theta$ 代表 $x$ 方向与 $t$ 方向的夹角，代表旋转 $-\theta$ 角度，改变坐标系。

已知运动方程

$\left\{ \begin{matrix}x=2t\\y=6-2t^2\end{matrix}\right.$

求 $\boldsymbol a_n,\boldsymbol a_t$。

利用好

$\boxed{\left\{ \begin{matrix}\boldsymbol a_t=\frac{\mathrm d v}{\mathrm d t}\\\boldsymbol a_n=\frac{v^2}{\rho}\\\boldsymbol a_t^2+\boldsymbol a_n^2=\boldsymbol a^2\end{matrix}\right.}$

$\boldsymbol v=\frac{\mathrm d \boldsymbol r}{\mathrm d t}=2\boldsymbol i-4t\boldsymbol j$

得到

$v=|\boldsymbol v|=2\sqrt{1+4t^2}$

得到

$|\boldsymbol a_t|=\frac{8t}{\sqrt{1+4t^2}}$

为了避免求 $\rho$，我们采用第三个公式。

$\boldsymbol a=\frac{\mathrm d \boldsymbol v}{\mathrm d t}=-4\boldsymbol j$

推出

$|\boldsymbol a_n|=\frac{4}{\sqrt{1+4t^2}}$

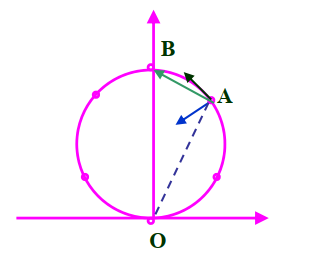
$T=6\, \mathrm s,R=3\,\mathrm m$ 走完一周，$t=0$ 时质点在 $O$ 处，$t=2s$ 时？

$\omega=\frac{2\pi}{T}=\frac{\pi}{3}$

$\boldsymbol r=(0,3)+3(\sin \omega t,-\cos \omega t)$

$\frac{\mathrm d \boldsymbol r}{\mathrm d t}|_{t=2s}=\underbrace{3\omega(\cos \omega t,\sin \omega t)}_{\boldsymbol v}=\left(-\frac{\pi}{2},\frac{\sqrt{3}\pi}{2}\right)$

$\frac{\mathrm d \boldsymbol v}{\mathrm d t}=3\omega^2(-\sin \omega t,\cos \omega t)$

$\frac{\mathrm d v}{\mathrm d t}=0$

匀速圆周运动。

$\int_A^B \mathrm d \boldsymbol r=\boldsymbol r_B-\boldsymbol r_A$

$\int_A^B \mathrm d |\boldsymbol r|=|\boldsymbol r_B|-|\boldsymbol r_A|$

$\int_A^B |\mathrm d \boldsymbol r|= s_{AB}$

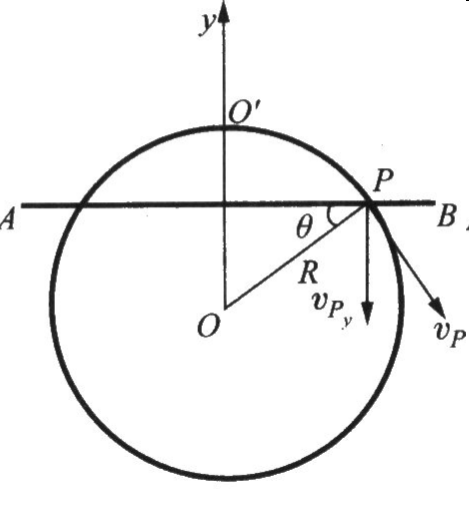
半径为 $R$ 的圆固定在竖直平面内，水平直棒 $AB$ 位于同一平面，从固定圆的最高点 $O'$ 由静止开始自由下落，如图所示。求：当直棒 $AB$下 落到离圆心 $O$ 距离为 $R/2$ 时，直棒与此圆交点 $P$ 的速率、切向加速度分量和法向加速度分量。

$P$ 是一个几何点而不是质点，轨迹在圆周上运动。

当距离 $R/2$ 时

$v_{P_y}=\sqrt{2gh}=\sqrt{2g\frac{R}{2}}=\sqrt{gR}$

$P$ 的速度可以分解为垂直于杆方向和沿杆方向，而垂直于杆方向就是 $v_{P_y}$，因此。

$v_p\cos \theta =v_{P_y}$

得到

$v_p=\frac{v_{P_y}}{\cos \theta}=2\sqrt{gR/3}$

法向加速度使用切向速度和半径计算：

$\boldsymbol a_n=\frac{v_P^2}{R}=\frac{4g}{3}$

根据线性代数的观点，为了计算 $\boldsymbol a_t$，我们既可以运用两者模长平方的关系，也可以利用某个分量上的关系。

$\boldsymbol a_y=-g$，$\boldsymbol a_x$ 未知，但是没有关系，我们已经可以通过投影的方式解出 $\boldsymbol a_t$。

$\boldsymbol a_n \sin \theta +\boldsymbol a_t\cos \theta=g$

得到

$a_t=\frac{g-a_n\sin\theta}{\cos \theta}=\frac{2\sqrt{3}}{9}g$

1
2
3

from sympy import *
from sympy.matrices import zeros 
import sympy

1
2

g,t,R = sympy.symbols('g t R')
v_p_y = g*t

1
2

theta = asin((R-1/2 * g * t**2)/R)
theta

$\displaystyle \operatorname{asin}{\left(\frac{R - 0.5 g t^{2}}{R} \right)}$

1
2

v_p = v_p_y/cos(theta)
simplify(v_p)

$\displaystyle \frac{g t}{\sqrt{1 - \frac{\left(R - 0.5 g t^{2}\right)^{2}}{R^{2}}}}$

1
2

a_n=v_p**2/R
simplify(a_n)

$\displaystyle \frac{1.0 R g}{1.0 R - 0.25 g t^{2}}$

1
2

a_t=(g-a_n*sin(theta))/cos(theta)
simplify(a_t)

$\displaystyle \frac{0.25 g^{2} t^{2}}{\sqrt{\frac{g t^{2} \cdot \left(1.0 R - 0.25 g t^{2}\right)}{R^{2}}} \cdot \left(1.0 R - 0.25 g t^{2}\right)}$


$\boldsymbol v=(v_1-v_2\tan\theta)\boldsymbol i-v_2 \boldsymbol j$

$\boldsymbol a =\frac{\mathrm d \boldsymbol v}{\mathrm d t}=-v_2 \frac{\mathrm d \tan\theta}{\mathrm d \theta}\cdot \frac{\mathrm d \theta}{\mathrm d t}\boldsymbol i=-v_2 \frac{1}{\cos^2 \theta }\cdot \frac{\mathrm d s}{R \mathrm d t}=-\frac{v_2^2}{\cos^3 \theta}$

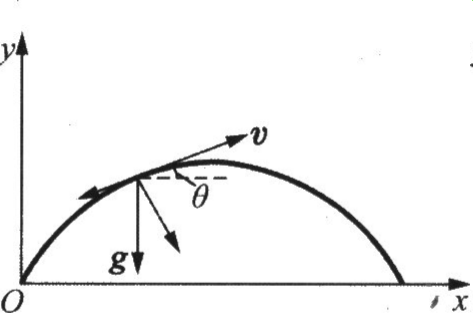
一质点以初速 $v_0$在与水平成仰角 $\theta_0$ 角的方向被抛出，忽略空气阻力，求质点在时刻 $t$ 的切向和法向加速度及曲率半径 $ρ$。

1

g,t,R,theta_0,v_0 = sympy.symbols('g t R theta_0 v_0')

1
2

v_x=v_0*cos(theta_0)
v_y=v_0*sin(theta_0)-g*t

1
2

v=sqrt(v_x**2+v_y**2)
v.simplify()

$\displaystyle \sqrt{g^{2} t^{2} - 2 g t v_{0} \sin{\left(\theta_{0} \right)} + v_{0}^{2}}$

1

theta=acos(v_x/v)

1
2

a_n=g*cos(theta)
a_n.simplify()

$\displaystyle \frac{g v_{0} \cos{\left(\theta_{0} \right)}}{\sqrt{g^{2} t^{2} - 2 g t v_{0} \sin{\left(\theta_{0} \right)} + v_{0}^{2}}}$

1
2

a_t=-g*sin(theta)
a_t.simplify()

$\displaystyle - g \sqrt{\frac{\left(g t - v_{0} \sin{\left(\theta_{0} \right)}\right)^{2}}{g^{2} t^{2} - 2 g t v_{0} \sin{\left(\theta_{0} \right)} + v_{0}^{2}}}$

1
2

rho=v**2/a_n
rho.simplify()

$\displaystyle \frac{\left(g^{2} t^{2} - 2 g t v_{0} \sin{\left(\theta_{0} \right)} + v_{0}^{2}\right)^{\frac{3}{2}}}{g v_{0} \cos{\left(\theta_{0} \right)}}$

设某一质点以初速度 $\boldsymbol v_0=100\boldsymbol i~(\mathrm{m\cdot s^{-1}})$ 做直线运动，其加速度为 $\boldsymbol a=-10 v\boldsymbol i~(\mathrm{m\cdot s^{-1}})$。 问：质点在停止运动之前运动的路程有多长？

第一种方法，得到 $v$ 与 $t$ 的关系，积分得到运动路程。

第二种方法，得到 $v$ 与 $s$ 的关系，直接得到路程：

$a=\frac{\mathrm d v}{\mathrm d t}=\frac{\mathrm d v}{\mathrm d s}\cdot\frac{\mathrm d s}{\mathrm d t}=-10v \Rightarrow \int_0^s \mathrm d s=-\frac{1}{10}\int_{100}^0 \mathrm d v$




习题

1-16


速度、加速度的合成。

1-22


既有切向加速度，又有法向加速度。

**1-24



数学法爆算：

$\sin \theta =\frac{R}{l} \quad \sin(\theta +\mathrm d \theta)=\frac{R}{l-v\mathrm d t}$

推出

$\underbrace{\sin \theta \cos \mathrm d \theta-\sin\theta}_{=0}+\underbrace{\sin\mathrm d \theta}_{\mathrm d\theta} \cos \theta=R\frac{v\mathrm d t}{l^2}$

也可以得到

$\omega=\frac{\mathrm d \theta}{\mathrm d t}=R\frac{v}{l^2 \cos \theta}=\frac{v\sin^2\theta}{R\cos \theta}$

1-26



1-48