12.3

12.4

**12.7

**12.8

利用刚体的动能:
Ek=21mv2+21Jcω2
因此,对于初状态,列出动能定理:
21m(2v)2+21(121ml2)(lv)2+21mv2=23mgl
得出
32mv2=ΔEp=23mgl
因此,得到 v=3/2gl
然后又得到
32mv′2=3mgl
推出 v′=3/2⋅gl。因此
F−mg=mlv′2⇒F=211mg
12.3
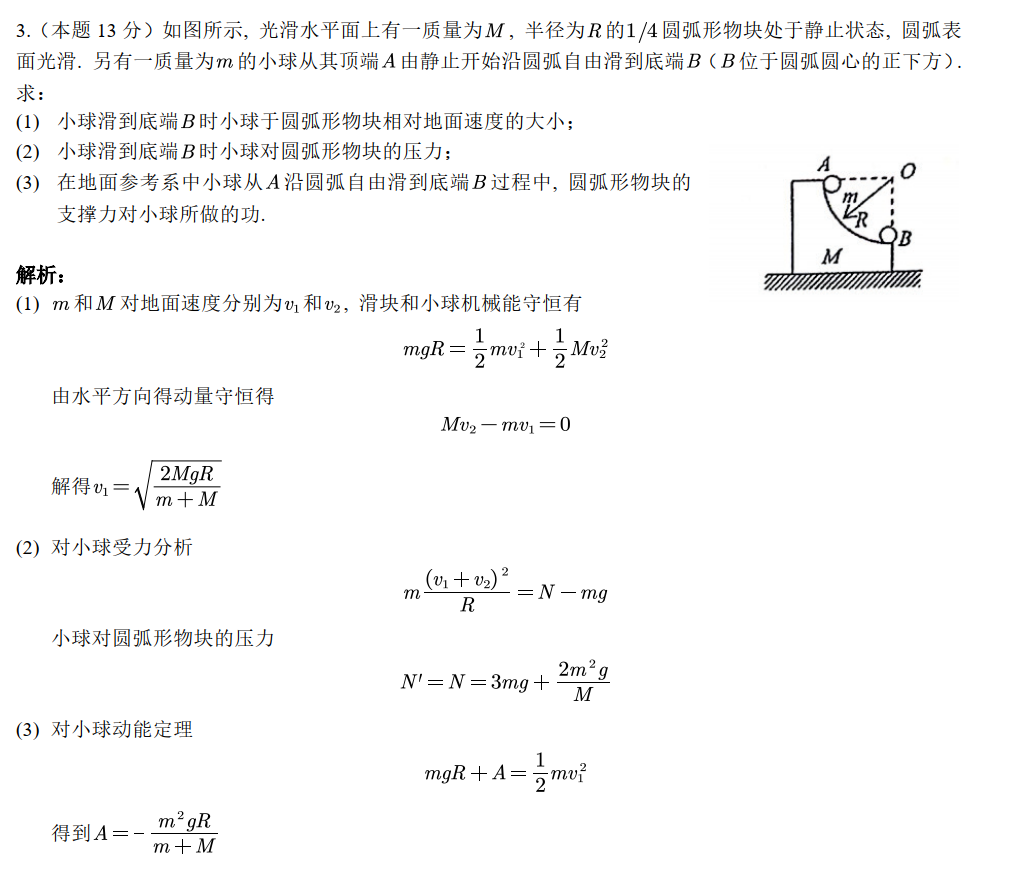
如果是圆弧形物块参考系,那么支持力做功为 0.
**12.4

由于空气与风筝之间无摩擦作用,所以风对风筝的作用力应该垂直于风筝的表面。因此,垂直于风筝表面的速度分量 vsinα 减为0,平行于风筝表面的速度分量 vcosα 不变。
13.1

13.2

最大动能 mg=F弹
13.3

13.4

**13.6

关键是式子列对,因为人是相对圆盘运动的,所以
Jω+m(ωR−u)R=0
13.8

弹簧的弹性势能为
41kx4
13.16
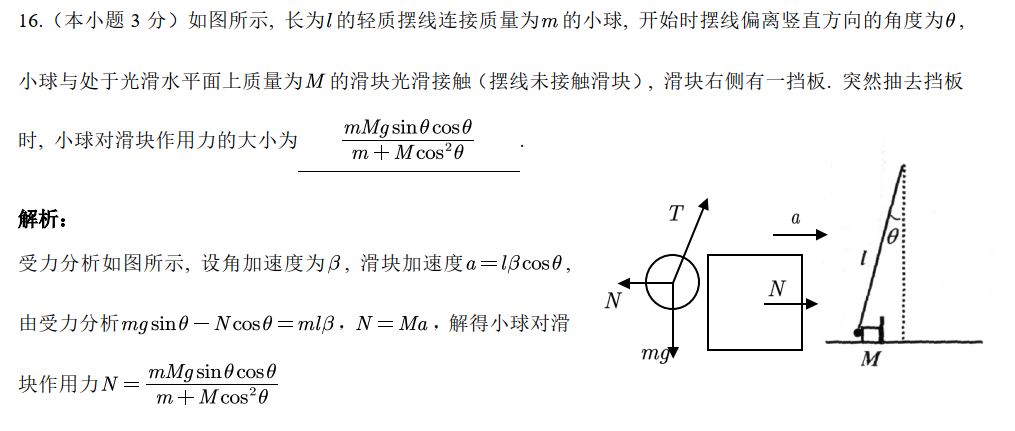
也可以观察到小球切向速度初始为 0,因此沿绳方向受力平衡,也就是
mgcosθ+Nsinθ=TTsinθ−N=maN=Ma
**13.4

(1) 能量守恒:
21mgl=21Jω2J=31ml2⇒ω=l3g
(2) 细杆角加速度
β=JM=ml2/3mgl/2=2l3g
质心运动定理:
ma=mg−Fya=β2l
得到 Fy=41mg,因此
N=41mg+Mg
(3) 系统移动最大距离
碰撞时,水平方向动量不守恒,但是角动量守恒,因此
Jω=Jω′+mvlv=ω′l
ω′=41ω
啊,小木块固定在木板上……动量守恒。
m2lω=(m+M)v
v=2(M+m)m3gl
最大距离:
s=2μgv2=8μ(M+m)23m2l
刚体运动的分解:质心速度+绕质心旋转速度(角速度),质心加速度+角加速度,动量+角动量
14.3

14.4

14.1



也可以整体分析。
14.3

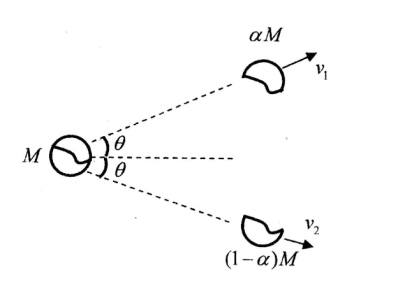
两个方向动量守恒,设一开始 M 运动的速度为 v:
{αMv1sinθ+(1−α)M(−v2)sinθ=0Mv=αMv1cosθ+(1−α)Mv2cosθ
得到
αv1=(1−α)v2=2cosθv=2McosθE:=p
然后除以下就行了
弹簧提供的能量由机械能守恒计算
−Ep=21αMv12+21(1−α)Mv22−E=21Mαp2+21M1−αp2−E
最小值当 α=1/2,然后能量是
Ep=Etan2θ
15.1

15.2

15.3`

对系统使用牛顿第二定律。
15.4

注意加速度正负号。
15.13

相对于轴的角动量:mvr,其中 r 为质点到轴的垂直距离。相对于点的角动量 mr×v。
15.14

15.15

相对于 O 点角动量守恒
m22lv0=[m1l2+m2(2l)2]ω
15.1

可以利用质心坐标不变:
m1+m2+mm1l−m2l=m1+m2+m(l−2s)m1+(2l−s)m
解得
s=2m1+mm1+m2+m2l
得到时间 t=s/u……
15.4

可以看做质量为负,使用平行轴定理。
J=21MR2+21(−m)r2+(−m)(2R)2
代入 m=R2r2M,得到
J=M(21R2−2R2r4−4r2)
重力作用于质心,因此,下面需要找出质心,显然纵坐标为 0,而横坐标:
xc=−m+MM⋅0+(−m)⋅21R=−2Rr2M−mM
得到
β=JM=J−xc⋅(M−m)g
而,由于质心运动定理:
(M−m)β(−xc)=(M−m)g−Fy
解出来 Fy 是这个鬼:
(M−R2Mr2)⎝⎛−4R2(M−R2Mr2)(0.5R2−4r2−2R2r4)Mgr4+g⎠⎞
后面,使用能量守恒:
0+21J⋅02=−(M−m)g⋅2Rr2M−mM+21Jω2
ω=JRr2Mg=2.0(2.0R4−R2r2−2r4Rgr2)0.5
**16.6


首先,明确是落地前瞬间,因此求的是瞬时值,需要代入
列出运动方程:
r=v0ti−21gt2j
求导即可得到
v=dtdr=v0i−gtj
代入 t=2h/g,得到(千万别忘了是在求落地瞬间)
dtdr=v0i−2ghj
再对 v 求导:
dtdv=−gj
再对 v 求导:
v=v02+g2t2dtdv=v02+g2t2g2t=v02+2ghg2gh
**16.7

还是使用对 OO′ 转轴角动量守恒:
mlv1+J⋅0=mlv2+J⋅ω⇒ω=ML23ml(v1−v2)
木板的动量大小,可以利用质心进行计算:
p=Mcv=M2Lω=2L3ml(v1−v2)
16.8

都是有心力。
16.9

16.10

利用机械能守恒、角动量守恒。
**16.1

ω0=(2m+M)R2mv0
设现在盘以 ω 的角速度旋转,那么摩擦力的力矩:
Mf=−∫rdF=−∫r⋅μ(2πrdr⋅σ)g
其中 σ=M/(πR2)。
得到
Mf=−32μMgR
那么,可以看出摩擦力的力矩与角速度无关,
Jω0+mR2+∫Mfdt=0⇒t=∣Mf∣mv0R=2μMg3mv0
16.2

得到劲度系数 k=mg/l0,碰撞前速度 v=2gh=2gl0,然后完全非弹性碰撞,两者速度都变为 gl0/2。
后面做简谐振动:
17.1

17.2

LO=−21mv0gt2k
也可以使用重力的冲力矩:
∫Mdt=∫0tv0t⋅mgdt=−21mv0gt2k
MO=−mgv0tk
dtdLO=−mgv0tk
17.3

机械能守恒,因为拉力不做功。角动量不守恒,因为拉力不是有心力。
17.5

这种题可以用垂直轴定理验证。好算的是对 z 轴的转动惯量:Jz=mR2
对 y 轴的转动惯量:
Jy=∫−2π2ππmdθ⋅(Rsinθ)2=πmR2⋅∫−π/2π/2sin2θdθ=2mR2
对 x 轴的转动惯量:
Jx=∫−2π2ππmdθ(Rcosθ)2=2mR2
由于位于 xoy 平面,所以
Jz=Jx+Jy
验证成立。
也可以补成完整圆环
17.14

一段绳子的速度应该是一致的,因此,v1=0,v2=gl。
vc=m1+m2m1v1+m2v2=4mgl/m=4gl
系统质心:
cy=m1+m2m1×83l+m2×(l/2+l/8)=(3/4×3/8+1/4×5/8)l=7l/16
B 端与质心距离:
2l−167l=16l
这时 A 脱离悬挂点
初态质心和 B 端相对速度为 3/4gl,末态相对速度为 0.
初态质心距离为 l/16,末态距离为 l/2。
所以
t=3/4gl167l=127gl
17.1

注:利用
dtdω=dφdω⋅dtdφ
类似于运动学。
18.1

18.2

F0mv02
18.3

右,1/3gtanθ.
18.4

m+Mmv0
t=v0s+mMs+l
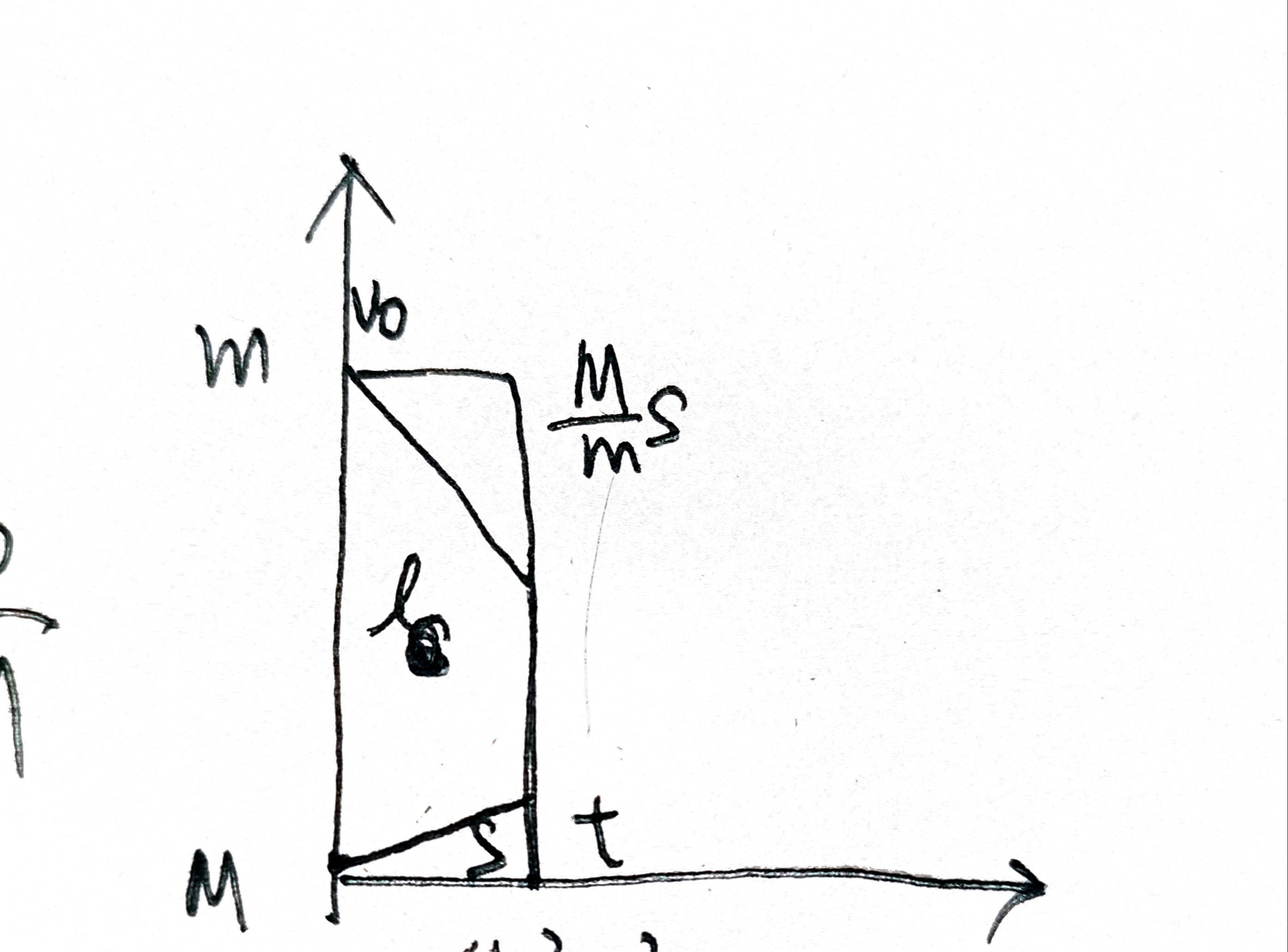
图是这样的。
也可以用运动表达式:
21Mft2=sv0t−21mft2=s+l
所以
t=v01[l+(mM+1)s]
18.8

同 17.5
18.9

t=kJln4
18.10
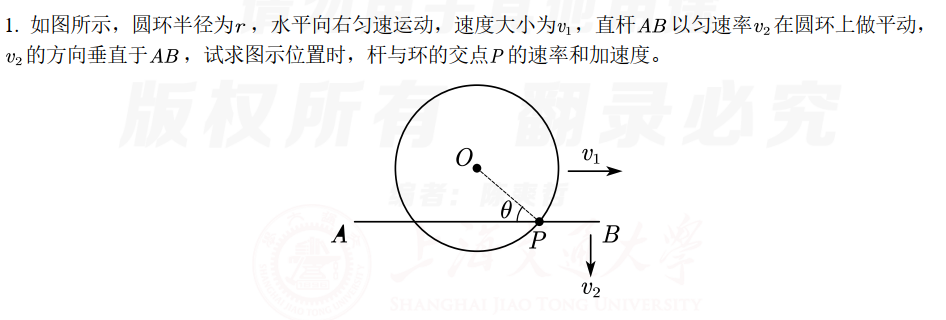
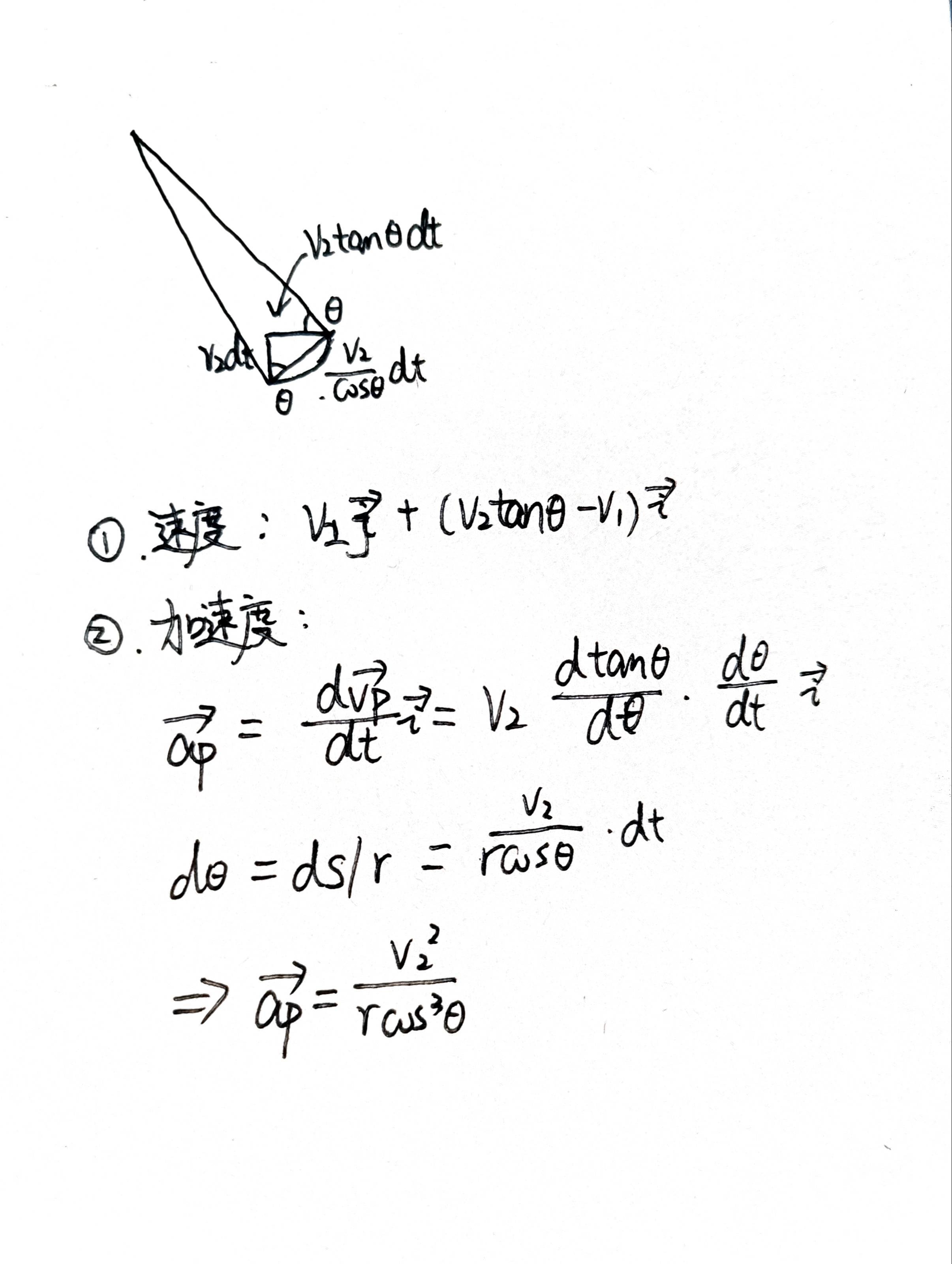
2r2a
Ep=∫r∞Fdr=∫r∞r3adr=2r2a
势能的定义:把物体移动到无穷远处(零势能点)时力做的功。
18.5

.jpg)
如果分析过程的话,比较复杂,但是注意到是恒力矩,给系统的冲力矩是可以算出的:
I=Mqm0=Jtω=(m0r2+21m0R2)ω⇒ω=q(2r2+R2)2M
结果是一样的。基本积出 ln(⋯)=ln(⋯),就可以说明是线性的,那么就可以用初末状态分析。
18.6

(1) 使用能量守恒:
21mv02=21kx2T=kx
v0>mkT2
细线会被拉断。
(2) 绳被拉断时,M 所受力为 T。长板获得最大加速度时,弹簧弹力最大,弹簧压缩程度最小,m,M 共速。
21kx2+21mvm2=21mv02
mvm=(M+m)v共21mv02=21(M+m)v共2+21kx2
a=Mkx=⋯
(3)
能量守恒:
21kx2+21mvm2=21mv02
21kx2+21mvm2=21MvM2
水平方向动量守恒(以水平向左为正方向):
mvm=MvM
v02=k(m−M)T2
所以,
v0=(m−M)kTm>M
19-2

19-5
质量为 m 的质点受到两个力的作用,一个是有心力 F1=f(r)er,另一个是摩擦力 F2=−λv(常数 λ>0),其中 v 是质点的速度。若初始时刻该质点对 r=0 的角动量为 L0,求以后各时刻质点角动量的大小。
有心力力矩为 0,这里积分情况比较复杂,难以分析,我们使用微分方程的形式。
M=dtdL
−λv×r=dtdL
两边取矢量模长
−rλvsinθ=dtdL
因为 L=mrvsinθ,所以,观察到相似的形式,得到
−λmL=dtdL
因此
L=L0e−mλt
19.6




需要特别关注细线拉紧的时候。
20.1
20.3

21.2

注意径向速度。事实上,速度的分解有三种:vx,vy;vt,vn;vθ,vr,都要考虑两个方向。
**21.3

利用系统整体动量定理,向下为正方向:
(Mg−N)dt=−λ4LgL+λ(4L−21vdt)(gL+gdt)
N=45Mg
也可以对作用力进行分解。一部分的作用力是为了提起来左边一段绳子
N1=43Mg
另一部分作用力和左边一部分绳子新增的长度有关:
N2dt=λ⋅21vdtgL=21Mgdt
因此 N=N1+N2=5Mg/4。

















































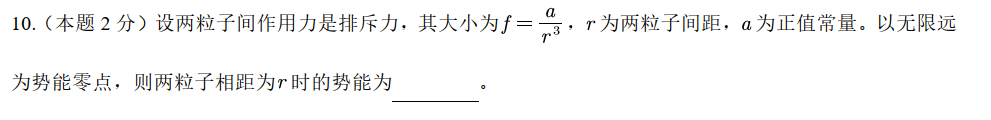

.jpg)









