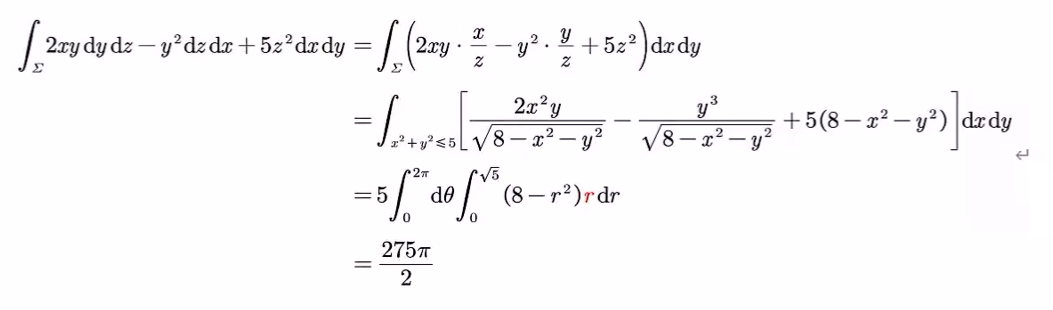基础知识
不定积分:找原函数的方法。
定积分:牛顿-莱布尼茨公式。
变上限函数:求导数。
二重积分:区间转化为平面。
三重积分:高斯积分。
引例:质线的质量
设有一条平面质线,占有 x o y xoy x o y C C C M ( x , y ) ∈ C M(x,y) \in C M ( x , y ) ∈ C ρ ( x , y ) ∈ C ( D ) \rho(x,y)\in C(D) ρ ( x , y ) ∈ C ( D )
基本思想 :局部以不变代变。
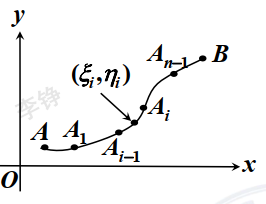
分割 :插入 n − 1 n-1 n − 1 A 0 = A , A n = B A_0=A,A_n=B A 0 = A , A n = B C C C n n n i i i A i − 1 A i ⌢ \overset{\LARGE{\frown}}{A_{i-1}A_i} A i − 1 A i ⌢ Δ s i \Delta s_i Δ s i
取值 在 A i − 1 A i ⌢ \overset{\LARGE{\frown}}{A_{i-1}A_i} A i − 1 A i ⌢ ( ξ i , η i ) (\xi_i,\eta_i) ( ξ i , η i ) ρ ( ξ i , η i ) \rho(\xi_i,\eta_i) ρ ( ξ i , η i )
求和
求极限 :当 λ = max 1 ≤ i ≤ n { Δ s i } → 0 \lambda=\max_{1\le i \le n}\{\Delta s_i\}\to 0 λ = max 1 ≤ i ≤ n { Δ s i } → 0
m = lim λ → 0 ∑ i = 1 n ρ ( ξ i , η i ) Δ s i m=\lim_{\lambda \to 0}\sum_{i=1}^n \rho(\xi_i,\eta_i) \Delta s_i
m = λ → 0 lim i = 1 ∑ n ρ ( ξ i , η i ) Δ s i
引申:形心怎么求?
x C = ∫ C d s ∫ C x d s x_C=\frac{\int_C \mathrm d s}{\int_C x\mathrm d s}
x C = ∫ C x d s ∫ C d s
质心怎么求?
x C = ∫ C ρ d s ∫ C x ρ d s x_C=\frac{\int _C \rho \mathrm d s}{\int_C x \rho \mathrm d s}
x C = ∫ C x ρ d s ∫ C ρ d s
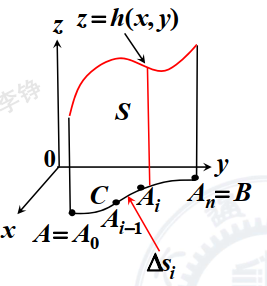
引例:柱面的面积
一张柱面 S S S x o y xoy x o y C C C z z z h ( x , y ) , ( x , y ) ∈ C h(x,y),(x,y)\in C h ( x , y ) , ( x , y ) ∈ C S S S
当 λ = max 1 ≤ i ≤ n { Δ s i } → 0 \lambda=\max_{1\le i \le n}\{\Delta s_i\}\to 0 λ = max 1 ≤ i ≤ n { Δ s i } → 0
S = lim λ → 0 ∑ i = 1 n h ( ξ i , η i ) Δ s i S=\lim_{\lambda \to 0}\sum_{i=1}^n h(\xi_i,\eta_i) \Delta s_i
S = λ → 0 lim i = 1 ∑ n h ( ξ i , η i ) Δ s i
定义 C C C x o y xoy x o y f ( x , y ) f(x,y) f ( x , y ) C C C C C C M 1 , M 2 , ⋯ , M n − 1 M_1,M_2,\cdots,M_{n-1} M 1 , M 2 , ⋯ , M n − 1 C C C n n n i i i ( ξ i , η i ) ( i = 1 , 2 , ⋯ , n ) (\xi_i,\eta_i)\, (i=1,2,\cdots,n) ( ξ i , η i ) ( i = 1 , 2 , ⋯ , n ) λ = max 1 ≤ i ≤ n { Δ s i } → 0 \displaystyle \lambda=\max_{1\le i \le n}\{\Delta s_i\}\to 0 λ = 1 ≤ i ≤ n max { Δ s i } → 0 ∑ i = 1 n f ( ξ i , η i ) Δ s i \displaystyle \sum_{i=1}^n f(\xi_i,\eta_i)\Delta s_i i = 1 ∑ n f ( ξ i , η i ) Δ s i I I I I I I f ( x , y ) f(x,y) f ( x , y ) C C C 对弧长的曲面积分(又称对弧长的曲线积分) ,记作
∫ C f ( x , y ) d s \int_C f(x,y)\mathrm d s
∫ C f ( x , y ) d s
曲线记号使用 C , Γ C,\Gamma C , Γ
其中 f ( x , y ) f(x,y) f ( x , y ) C C C d s \mathrm d s d s
性质 f ( x , y ) f(x,y) f ( x , y ) C C C ∫ C f ( x , y ) d s \int_C f(x,y) \mathrm d s ∫ C f ( x , y ) d s
性质
∫ C k ⋅ f ( x , y ) d s = k ⋅ ∫ C f ( x , y ) d s \displaystyle \int_C k\cdot f(x,y) \mathrm d s=k\cdot \int_C f(x,y)\mathrm d s ∫ C k ⋅ f ( x , y ) d s = k ⋅ ∫ C f ( x , y ) d s k k k ∫ C [ f ( x , y ) + g ( x , y ) ] d s = ∫ C f ( x , y ) d s + ∫ C g ( x , y ) d s \displaystyle \int_C[f(x,y)+g(x,y)]\mathrm d s=\int_C f(x,y)\mathrm d s+\int_C g(x,y)\mathrm d s ∫ C [ f ( x , y ) + g ( x , y ) ] d s = ∫ C f ( x , y ) d s + ∫ C g ( x , y ) d s ∫ C 1 + C 2 f ( x , y ) d s = ∫ C 1 f ( x , y ) d s + ∫ C 2 f ( x , y ) d s \displaystyle \int_{C_1+C_2} f(x,y)\mathrm d s=\int_{C_1} f(x,y)\mathrm d s+\int_{C_2} f(x,y)\mathrm d s ∫ C 1 + C 2 f ( x , y ) d s = ∫ C 1 f ( x , y ) d s + ∫ C 2 f ( x , y ) d s 中值定理:设函数 f ( x , y ) f(x,y) f ( x , y ) C C C ∃ ( ξ , η ) ∈ C \exists (\xi,\eta)\in C ∃ ( ξ , η ) ∈ C ∫ C f ( x , y ) d s = f ( ξ , η ) ⋅ S C \displaystyle \int_C f(x,y)\mathrm d s=f(\xi,\eta)\cdot S_C ∫ C f ( x , y ) d s = f ( ξ , η ) ⋅ S C S C S_C S C C C C S C = ∫ C 1 ⋅ d s \displaystyle S_C=\int_C1\cdot \mathrm ds S C = ∫ C 1 ⋅ d s
定理 C C C
{ x = x ( t ) y = y ( t ) ( α ≤ t ≤ β ) \left\{ \begin{matrix}x=x(t)\\y=y(t)\end{matrix}\right. \quad (\alpha \le t \le \beta)
{ x = x ( t ) y = y ( t ) ( α ≤ t ≤ β )
其中 x ( t ) , y ( t ) x(t),y(t) x ( t ) , y ( t ) 连续导数 ,由于弧微分
d s = ( d x ) 2 + ( d y ) 2 = x ′ ( t ) 2 + y ′ ( t ) 2 d t \mathrm d s=\sqrt{(\mathrm d x)^2+(\mathrm d y)^2}=\sqrt{x'(t)^2+y'(t)^2}\mathrm d t
d s = ( d x ) 2 + ( d y ) 2 = x ′ ( t ) 2 + y ′ ( t ) 2 d t
所以
∫ C f ( x , y ) d s = ∫ α β f [ x ( t ) , y ( t ) ] ⋅ x ′ ( t ) 2 + y ′ ( t ) 2 d t \boxed{\int_C f(x,y) \mathrm d s=\int_{\alpha}^\beta f[x(t),y(t)] \cdot\sqrt{x'(t)^2+y'(t)^2}\mathrm d t}
∫ C f ( x , y ) d s = ∫ α β f [ x ( t ) , y ( t ) ] ⋅ x ′ ( t ) 2 + y ′ ( t ) 2 d t
证明使用 积分中值定理 。
当曲线方程为 y = y ( x ) ( a ≤ x ≤ b ) y=y(x)\quad (a\le x\le b) y = y ( x ) ( a ≤ x ≤ b )
∫ C f ( x , y ) d s = ∫ a b f [ x , y ( x ) ] ⋅ 1 + y ′ ( x ) 2 d x \boxed{\int_C f(x,y) \mathrm d s=\int_{a}^b f[x,y(x)] \cdot\sqrt{1+y'(x)^2}\mathrm d x}
∫ C f ( x , y ) d s = ∫ a b f [ x , y ( x ) ] ⋅ 1 + y ′ ( x ) 2 d x
当曲线采用极坐标,极坐标化为参数方程,
{ x = r ( θ ) sin θ y = r ( θ ) cos θ ( α ≤ θ ≤ β ) \left\{ \begin{matrix}x=r(\theta)\sin\theta \\y=r(\theta)\cos\theta\end{matrix}\right. \quad (\alpha \le \theta \le \beta)
{ x = r ( θ ) sin θ y = r ( θ ) cos θ ( α ≤ θ ≤ β )
得到
∫ C f ( x , y ) d s = ∫ α β f ( r cos θ , r sin θ ) r 2 ( θ ) + r ′ 2 ( θ ) d θ \boxed{\int_C f(x,y)\mathrm d s=\int_\alpha^\beta f(r\cos\theta,r\sin\theta) \sqrt{r^2(\theta)+r'^2(\theta)} \mathrm d \theta}
∫ C f ( x , y ) d s = ∫ α β f ( r cos θ , r sin θ ) r 2 ( θ ) + r ′ 2 ( θ ) d θ
例题1 ∫ C y 2 d s \displaystyle \int_C y^2 \mathrm d s ∫ C y 2 d s C C C x = a ( t − sin t ) , y = a ( 1 − cos t ) ( 0 ≤ t ≤ 2 π , a > 0 ) x=a(t-\sin t),y=a(1-\cos t)\,(0\le t \le 2\pi ,a >0) x = a ( t − sin t ) , y = a ( 1 − cos t ) ( 0 ≤ t ≤ 2 π , a > 0 )
先写出 x ′ ( t ) , y ′ ( t ) x'(t),y'(t) x ′ ( t ) , y ′ ( t )
d s = 2 a ∣ sin t 2 ∣ d t \mathrm d s=2a\left|\sin \frac{t}{2}\right|\mathrm d t
d s = 2 a ∣ ∣ ∣ ∣ sin 2 t ∣ ∣ ∣ ∣ d t
∫ C y 2 d s = ∫ 0 2 π a 2 ( 1 − cos t ) 2 ⋅ 2 a ∣ sin t 2 ∣ d t = 8 a 3 ∫ 0 2 π sin 5 t 2 d t = 32 a 3 ∫ 0 π 2 sin 5 u d u = 2 8 a 3 15 \int_C y^2 \mathrm d s=\int_0^{2\pi} a^2(1-\cos t)^2 \cdot 2 a \left|\sin \frac{t}{2}\right| \mathrm d t\\
=8a^3 \int_0^{2\pi} \sin^5 \frac{t}{2}\mathrm d t=32 a^3\int_0^\frac{\pi}{2} \sin^5 u \mathrm d u=\frac{2^8a^3}{15}
∫ C y 2 d s = ∫ 0 2 π a 2 ( 1 − cos t ) 2 ⋅ 2 a ∣ ∣ ∣ ∣ sin 2 t ∣ ∣ ∣ ∣ d t = 8 a 3 ∫ 0 2 π sin 5 2 t d t = 3 2 a 3 ∫ 0 2 π sin 5 u d u = 1 5 2 8 a 3
例题2


例题3

先记下点 A ( a , 0 ) , B ( 2 a / 2 , 2 a / 2 ) A(a,0),B\left(\sqrt{2}a/2,\sqrt{2}a/2\right) A ( a , 0 ) , B ( 2 a / 2 , 2 a / 2 )
则
∮ C e x 2 + y 2 d s = ∫ O A ‾ + ∫ A B ⌢ + ∫ O B ‾ \oint_C e^{\sqrt{x^2+y^2}} \mathrm d s=\int_{\overline{OA}}+\int_{\overset{\LARGE{\frown}}{AB}}+\int_{\overline{OB}}
∮ C e x 2 + y 2 d s = ∫ O A + ∫ A B ⌢ + ∫ O B
对于 ∫ A B ⌢ \int_{\overset{\LARGE{\frown}}{AB}} ∫ A B ⌢ x = a cos t , y = a sin t x=a\cos t,y=a\sin t x = a cos t , y = a sin t
∫ α β f ( r cos θ , r sin θ ) r 2 ( θ ) + r ′ 2 ( θ ) d θ = ∫ 0 π 4 e a a d θ \int_\alpha^\beta f(r\cos\theta,r\sin\theta) \sqrt{r^2(\theta)+r'^2(\theta)} \mathrm d \theta=\int_0^\frac{\pi}{4} e^a a\mathrm d \theta
∫ α β f ( r cos θ , r sin θ ) r 2 ( θ ) + r ′ 2 ( θ ) d θ = ∫ 0 4 π e a a d θ
例题4

方法1 参数方程。令 x = R + R cos θ , y = R sin θ x=R+R\cos \theta,y=R\sin\theta x = R + R cos θ , y = R sin θ d s = R d t \mathrm d s=R\mathrm d t d s = R d t
所以
∫ C ( x 2 + y 2 ) d s = ∫ 0 π 2 R ⋅ ( R + R cos t ) ⏟ 2 R x R d t = 2 π R 3 \int_C (x^2+y^2)\mathrm d s=\int_0^\pi \underbrace{2R \cdot (R+R\cos t)}_{2Rx}R\mathrm d t=2\pi R^3
∫ C ( x 2 + y 2 ) d s = ∫ 0 π 2 R x 2 R ⋅ ( R + R cos t ) R d t = 2 π R 3
是可以代入的。
方法2 利用极坐标,曲线方程为 r = 2 R cos θ r=2R\cos\theta r = 2 R cos θ
性质
如果 积分曲线 C \boldsymbol C C y \boldsymbol y y ,且 f ( x , y ) f(x,y) f ( x , y ) 关于 x \boldsymbol x x ,则
∫ C f ( x , y ) d s = 0 \int_C f(x,y)\mathrm d s=0
∫ C f ( x , y ) d s = 0
和二重积分的对称性类似。
例题5
设曲线 C C C x 2 4 + y 2 3 = 1 \displaystyle \frac{x^2}{4}+\frac{y^2}{3}=1 4 x 2 + 3 y 2 = 1 a a a
∫ C ( 3 x 2 + 4 y 2 + 2 x y + 3 x 2 y + 4 x y 2 ⏟ 0 ) d s \int_C (3x^2+4y^2+\underbrace{2xy+3x^2y+4xy^2}_{0})\mathrm d s
∫ C ( 3 x 2 + 4 y 2 + 0 2 x y + 3 x 2 y + 4 x y 2 ) d s
不考虑原点对称,而 x y = − ( − x ⋅ y ) xy=-(-x\cdot y) x y = − ( − x ⋅ y )
3 x 2 + 4 y 2 = 12 3x^2+4y^2=12 3 x 2 + 4 y 2 = 1 2 12 a 12a 1 2 a
例题6
设曲线 C C C x 2 + y 2 = a 2 \displaystyle x^2+y^2=a^2 x 2 + y 2 = a 2
∮ C ( 3 x 2 + 4 y 2 + 2 x y ) d s \oint_C (3x^2+4y^2+2xy)\mathrm d s
∮ C ( 3 x 2 + 4 y 2 + 2 x y ) d s
∮ C x 2 d s = ∮ C y 2 d s \oint_C x^2\mathrm d s=\oint_C y^2 \mathrm d s
∮ C x 2 d s = ∮ C y 2 d s
等于
7 2 ∮ C ( x 2 + y 2 ) d s = 7 2 2 π a ⋅ a 2 = 7 π a 3 \frac{7}{2}\oint_C (x^2+y^2)\mathrm d s=\frac{7}{2}2\pi a \cdot a^2=7\pi a^3
2 7 ∮ C ( x 2 + y 2 ) d s = 2 7 2 π a ⋅ a 2 = 7 π a 3
设空间曲线方程为
Γ : { x = x ( t ) y = y ( t ) z = z ( t ) ( α ≤ t ≤ β ) \Gamma:\left\{
\begin{aligned}
&x=x(t)\\
&y=y(t)\\
&z=z(t)
\end{aligned}
\right.
\, (\alpha\le t \le \beta)
Γ : ⎩ ⎪ ⎨ ⎪ ⎧ x = x ( t ) y = y ( t ) z = z ( t ) ( α ≤ t ≤ β )
则第一类空间曲线积分:
∫ Γ f ( x , y , z ) d s = ∫ α β f [ x ( t ) , y ( t ) , z ( t ) ] ⋅ x ′ ( t ) 2 + y ′ ( t ) 2 + z ′ ( t ) 2 d t \boxed{\int_\Gamma f(x,y,z)\mathrm d s=\int_{\alpha}^\beta f[x(t),y(t),z(t)]\cdot \sqrt{x'(t)^2+y'(t)^2+z'(t)^2}\mathrm d t}
∫ Γ f ( x , y , z ) d s = ∫ α β f [ x ( t ) , y ( t ) , z ( t ) ] ⋅ x ′ ( t ) 2 + y ′ ( t ) 2 + z ′ ( t ) 2 d t
例题7 计算曲线积分 ∫ Γ y ( x − z ) d s \displaystyle \int_\Gamma y(x-z)\mathrm d s ∫ Γ y ( x − z ) d s Γ \Gamma Γ x 2 4 + y 2 2 + z 2 4 = 1 \displaystyle \frac{x^2}{4}+\frac{y^2}{2}+\frac{z^2}{4}=1 4 x 2 + 2 y 2 + 4 z 2 = 1 x + z = 2 x+z=2 x + z = 2 ( 2 , 0 , 0 ) (2,0,0) ( 2 , 0 , 0 ) ( 1 , 1 , 1 ) (1,1,1) ( 1 , 1 , 1 )
得到 x 2 + y 2 = 2 x x^2+y^2=2x x 2 + y 2 = 2 x x : = cos θ + 1 , y : = sin θ x:=\cos \theta+1,y:=\sin\theta x : = cos θ + 1 , y : = sin θ z = 1 − cos θ z=1-\cos\theta z = 1 − cos θ
d s = 1 + sin 2 t d t \mathrm d s=\sqrt{1+\sin^2 t} \mathrm d t
d s = 1 + sin 2 t d t
则两点之间相对于 θ \theta θ θ = 0 → θ = π / 2 \theta=0 \to \theta=\pi/2 θ = 0 → θ = π / 2
∫ Γ y ( x − z ) d s = ∫ 0 π 2 sin t ⋅ 2 cos t ⋅ 1 + sin 2 t d t = 2 ( 2 2 − 1 ) 3 \int_\Gamma y(x-z) \mathrm d s=\int_0^\frac{\pi}{2} \sin t\cdot 2\cos t \cdot \sqrt{1+\sin^2 t }\mathrm d t=\frac{2(2\sqrt{2}-1)}{3}
∫ Γ y ( x − z ) d s = ∫ 0 2 π sin t ⋅ 2 cos t ⋅ 1 + sin 2 t d t = 3 2 ( 2 2 − 1 )
引例:变力沿曲线做功
设有一个质点,在 x o y xoy x o y C C C A A A B B B
F ( x , y ) = P ( x , y ) i + Q ( x , y ) j \boldsymbol F(x,y)=P(x,y)\boldsymbol i+Q(x,y)\boldsymbol j
F ( x , y ) = P ( x , y ) i + Q ( x , y ) j
的作用,计算 F \boldsymbol F F C C C F \boldsymbol F F 点积 。
设曲线弧 C C C A A A B B B C + C^+ C + B B B A A A C − C^- C −
取曲线上任意点 M ( x , y ) M(x,y) M ( x , y ) C + C^+ C + d s \mathrm d \boldsymbol s d s d W = F ⋅ d s \mathrm d W=\boldsymbol F\cdot \mathrm d \boldsymbol s d W = F ⋅ d s
若记 d s = { cos α , cos β } d s = { d x , d y } \mathrm d \boldsymbol s=\{\cos \alpha,\cos \beta\}\mathrm d s=\{\mathrm d x,\mathrm d y\} d s = { cos α , cos β } d s = { d x , d y }
W = ∫ C [ P ( x , y ) cos α + Q ( x , y ) cos β ] d s = ∫ C P ( x , y ) d x + Q ( x , y ) d y W=\int_C [P(x,y)\cos \alpha+ Q(x,y)\cos \beta]\mathrm d s=\int_C P(x,y)\mathrm d x+Q(x,y)\mathrm d y
W = ∫ C [ P ( x , y ) cos α + Q ( x , y ) cos β ] d s = ∫ C P ( x , y ) d x + Q ( x , y ) d y



与第一类曲线积分类似于第二类曲面积分有相似的性质如:线性性质、区域可加性等。还有特殊的性质,当曲线弧方向相反之后:
∫ C − P ( x , y ) d x + Q ( x , y ) d y = − ∫ C + P ( x , y ) d x + Q ( x , y ) d y \int_{C^-} P(x,y)\mathrm{d} x+Q(x,y)\mathrm{d} y=-\int_{C^+} P(x,y) \mathrm{d} x+Q(x,y) \mathrm{d} y
∫ C − P ( x , y ) d x + Q ( x , y ) d y = − ∫ C + P ( x , y ) d x + Q ( x , y ) d y
然而不考虑对称性。
∫ C P ( x , y ) d x + Q ( x , y ) d y = ∫ α β ( P x ′ + Q y ′ ) d t \boxed{\int_C P(x,y)\mathrm d x+Q(x,y)\mathrm d y=\int_\alpha^\beta (Px'+Qy')\mathrm d t}
∫ C P ( x , y ) d x + Q ( x , y ) d y = ∫ α β ( P x ′ + Q y ′ ) d t


和路径无关。
设空间曲线方程为 Γ : { x = x ( t ) y = y ( t ) z = z ( t ) \Gamma:\left\{
\begin{aligned}
&x=x(t)\\
&y=y(t)\\&z=z(t)\\
\end{aligned}
\right. Γ : ⎩ ⎪ ⎨ ⎪ ⎧ x = x ( t ) y = y ( t ) z = z ( t ) t t t α \alpha α β \beta β
∫ Γ P ( x , y , z ) d x + Q ( x , y , z ) d y + R ( x , y , z ) d z = ∫ α β { P [ x ( t ) , y ( t ) , z ( t ) ] x ′ ( t ) + Q [ x ( t ) , y ( t ) , z ( t ) ] y ′ ( t ) + R [ x ( t ) , y ( t ) , z ( t ) ] z ′ ( t ) } d t \int_\Gamma P(x,y,z) \mathrm{d} x+Q(x,y,z)\mathrm{d} y+R(x,y,z)\mathrm{d} z\\=\int_{\alpha}^\beta \left\{P[x(t),y(t),z(t)]x'(t)+Q[x(t),y(t),z(t)]y'(t)+R[x(t),y(t),z(t)]z'(t)\right\}\mathrm d t
∫ Γ P ( x , y , z ) d x + Q ( x , y , z ) d y + R ( x , y , z ) d z = ∫ α β { P [ x ( t ) , y ( t ) , z ( t ) ] x ′ ( t ) + Q [ x ( t ) , y ( t ) , z ( t ) ] y ′ ( t ) + R [ x ( t ) , y ( t ) , z ( t ) ] z ′ ( t ) } d t


也可以观察到 d ( x y z ) = d ( ξ η ς t 3 ) = 3 ξ η ς t 2 d t \mathrm d (xyz)=\mathrm d (\xi \eta \varsigma t^3)=3\xi\eta\varsigma t ^2 \mathrm d t d ( x y z ) = d ( ξ η ς t 3 ) = 3 ξ η ς t 2 d t
因此,就是求 ξ η ς \xi\eta\varsigma ξ η ς
利用方向余弦
{ cos α , cos β , cos γ } = 1 x ′ ( t ) 2 + y ′ ( t ) 2 + z ′ ( t ) 2 { x ′ ( t ) , y ′ ( t ) , z ′ ( t ) } \{\cos \alpha,\cos \beta,\cos \gamma \}=\frac{1}{\sqrt{x'(t)^2+y'(t)^2+z'(t)^2}}\{x'(t),y'(t),z'(t)\}
{ cos α , cos β , cos γ } = x ′ ( t ) 2 + y ′ ( t ) 2 + z ′ ( t ) 2 1 { x ′ ( t ) , y ′ ( t ) , z ′ ( t ) }
进行投影,和单位方向向量点乘相当于投影。
另外一种方法,利用 d s = ( d x ) 2 + ( d y ) 2 + ( d z ) 2 \mathrm d s=\sqrt{(\mathrm d x)^2+(\mathrm d y)^2+(\mathrm{d} z)^2} d s = ( d x ) 2 + ( d y ) 2 + ( d z ) 2
∫ Γ P d x + Q d y + R d z = ∫ Γ P d x d t + Q d y d t + R d z d t ( d x / d t ) 2 + ( d y / d t ) 2 + ( d z / d t ) 2 d s \int_\Gamma P\mathrm d x+Q\mathrm d y+R\mathrm d z=\int_\Gamma \frac{P\frac{\mathrm d x}{\mathrm d t}+Q\frac{\mathrm d y}{\mathrm d t}+R\frac{\mathrm d z}{\mathrm d t}}{\sqrt{(\mathrm d x/\mathrm d t)^2+(\mathrm d y/\mathrm d t)^2+(\mathrm d z/\mathrm d t)^2}}\mathrm d s
∫ Γ P d x + Q d y + R d z = ∫ Γ ( d x / d t ) 2 + ( d y / d t ) 2 + ( d z / d t ) 2 P d t d x + Q d t d y + R d t d z d s
例题12 设 Γ \Gamma Γ x = t , y = t 2 , z = t 3 x=t,y=t^2,z=t^3 x = t , y = t 2 , z = t 3 t t t 0 0 0 1 1 1 ∫ Γ P d x + Q d y + R d z \displaystyle \int_\Gamma P\mathrm{d} x+Q\mathrm{d} y+R\mathrm{d} z ∫ Γ P d x + Q d y + R d z
∫ Γ P d x + Q d y + R d z = ∫ Γ P + 2 t Q + 3 t 2 R 1 + 4 t 2 + 9 t 4 d s \displaystyle \int_\Gamma P\mathrm{d} x+Q\mathrm{d} y+R\mathrm{d} z=\int_\Gamma \frac{P+2tQ+3t^2 R}{\sqrt{1+4t^2+9t^4}} \mathrm{d} s
∫ Γ P d x + Q d y + R d z = ∫ Γ 1 + 4 t 2 + 9 t 4 P + 2 t Q + 3 t 2 R d s
对于封闭有向曲线的积分,可以转化为其围成区域内部的积分
设闭区域 D D D C C C P ( x , y ) , Q ( x , y ) P(x,y),Q(x,y) P ( x , y ) , Q ( x , y ) D D D
∬ D ( ∂ Q ∂ x − ∂ P ∂ y ) d x d y = ∮ C P d x + Q d y \iint_D \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \mathrm d x\mathrm d y=\oint_C P\mathrm d x+Q\mathrm d y
∬ D ( ∂ x ∂ Q − ∂ y ∂ P ) d x d y = ∮ C P d x + Q d y
其中 C C C D D D 取正向 的整个边界,正向是逆时针。称为格林公式。



设曲线 C C C D D D F = { f ( x , y ) , g ( x , y ) } \boldsymbol F=\{f(x,y),g(x,y)\} F = { f ( x , y ) , g ( x , y ) } D D D C C C e τ = { cos α , cos β } \boldsymbol e_{\tau}=\{\cos \alpha,\cos \beta\} e τ = { cos α , cos β } n 0 = { cos β , − cos α } \boldsymbol n^0=\{\cos \beta,-\cos \alpha\} n 0 = { cos β , − cos α }
则 ( F ⋅ n 0 ) d s = f cos β d s − g cos α d s = f d y − g d x (\boldsymbol F\cdot \boldsymbol n^0)\mathrm{d} s=f\cos \beta \mathrm{d} s-g\cos\alpha \mathrm{d} s=f\mathrm{d} y-g\mathrm{d} x ( F ⋅ n 0 ) d s = f cos β d s − g cos α d s = f d y − g d x
此时 ∮ C ( F ⋅ n 0 ) d s = ∮ C f d y − g d x = ∬ D ( ∂ f ∂ x + ∂ g ∂ y ) d σ \displaystyle \oint_C (\boldsymbol F\cdot \boldsymbol n^0)\mathrm{d} s=\oint_C f\mathrm{d}y-g\mathrm{d}x=\iint_D \left(\frac{\partial f}{\partial x}+\frac{\partial g}{\partial y}\right) \mathrm{d} \sigma ∮ C ( F ⋅ n 0 ) d s = ∮ C f d y − g d x = ∬ D ( ∂ x ∂ f + ∂ y ∂ g ) d σ
记梯度算子为:∇ = { ∂ ∂ x , ∂ ∂ y } \displaystyle \nabla=\left\{\frac{\partial}{\partial x},\frac{\partial}{\partial y}\right\} ∇ = { ∂ x ∂ , ∂ y ∂ } ∇ ⋅ F = ∂ f ∂ x + ∂ g ∂ y \displaystyle \nabla\cdot \boldsymbol F=\frac{\partial f}{\partial x}+\frac{\partial g}{\partial y} ∇ ⋅ F = ∂ x ∂ f + ∂ y ∂ g
∮ C ( F ⋅ n 0 ) d s = ∬ D ( ∇ ⋅ F ) d σ \oint_C (\boldsymbol F\cdot \boldsymbol n^0)\mathrm{d} s = \iint_D (\nabla \cdot \boldsymbol F)\mathrm d \sigma
∮ C ( F ⋅ n 0 ) d s = ∬ D ( ∇ ⋅ F ) d σ
格林公式求面积:
S ( D ) = ∮ C − y d x = ∮ C x d y = 1 2 ∮ C − y d x + x d y S(D)=\oint_C -y\mathrm{d} x=\oint_C x \mathrm{d} y=\frac{1}{2} \oint_C -y\mathrm{d} x+x\mathrm{d} y
S ( D ) = ∮ C − y d x = ∮ C x d y = 2 1 ∮ C − y d x + x d y

这样的形式比较对称,曲线的图形如下:

解法一:直接计算曲线积分,代入 y = x 2 y=x^2 y = x 2 ∫ − 1 1 ( e x 2 + 2 x 2 e x 2 ) d x \displaystyle \int_{-1}^1 \left(e^{x^2}+2x^2 e^{x^2}\right)\mathrm{d} x ∫ − 1 1 ( e x 2 + 2 x 2 e x 2 ) d x
分部积分:∫ e x 2 d x = x e x 2 − ∫ 2 x 2 e x 2 d x \displaystyle \int e^{x^2} \mathrm{d} x=xe^{x^2}-\int 2x^2 e^{x^2} \mathrm{d} x ∫ e x 2 d x = x e x 2 − ∫ 2 x 2 e x 2 d x x e x 2 + C xe^{x^2}+C x e x 2 + C


计算曲线积分 I = ∫ C e − y 2 d x + 2 x ( 1 − y e − y 2 ) d y \displaystyle I=\int_C e^{-y^2} \mathrm{d} x+2x (1-ye^{-y^2})\mathrm{d} y I = ∫ C e − y 2 d x + 2 x ( 1 − y e − y 2 ) d y C C C y = x y=x y = x O ( 0 , 0 ) O(0,0) O ( 0 , 0 ) A ( 1 , 1 ) A(1,1) A ( 1 , 1 )
解法一 直接计算,所得定积分比较复杂。
解法二 使用格林公式,需要保证曲线正向、闭合。
设 B ( 0 , 1 ) B(0,1) B ( 0 , 1 )
L A B : y = 1 , x : 1 → 0 ; L B O : x = 0 , y : 1 → 0 L_{\over{AB}}: y=1,x:1\to0;L_{\over{BO}}:x=0,y:1\to0
L A B : y = 1 , x : 1 → 0 ; L B O : x = 0 , y : 1 → 0
由格林公式得
设平面曲线 C C C x 2 + y 2 = 1 x^2+y^2=1 x 2 + y 2 = 1 ∮ C x e 2 x 2 − 3 y 2 d x + y e 2 x 2 − 3 y 2 d y \displaystyle \oint_C x e^{2x^2-3y^2}\mathrm d x+y e^{2x^2-3y^2} \mathrm d y ∮ C x e 2 x 2 − 3 y 2 d x + y e 2 x 2 − 3 y 2 d y
第一是可以用 y 2 = 1 − x 2 , x 2 = 1 − y 2 y^2=1-x^2,x^2=1-y^2 y 2 = 1 − x 2 , x 2 = 1 − y 2 凑微分 得到结果为 0.
第二是可以直接使用 Green 公式,得到
∬ D − 2 x y e 2 x 2 − 3 y 2 d σ \iint_{D} -2xy e^{2x^2-3y^2}\mathrm{d} \sigma
∬ D − 2 x y e 2 x 2 − 3 y 2 d σ
之后注意到对称性,结果为0.
第三是最简单的参数化解法,令 x = cos t , y = sin t , t ∈ [ 0 , 2 π ) x=\cos t,y=\sin t ,t \in [0,2\pi) x = cos t , y = sin t , t ∈ [ 0 , 2 π )
∮ C [ cos t ( − sin t ) e 2 x 2 − 3 y 2 + sin t cos t e 2 x 2 − 3 y 3 ] d t \oint_C \left[\cos t(-\sin t ) e^{2x^2-3y^2}+\sin t \cos t e^{2x^2-3y^3}\right]\mathrm d t
∮ C [ cos t ( − sin t ) e 2 x 2 − 3 y 2 + sin t cos t e 2 x 2 − 3 y 3 ] d t
结果为 0.
设 G G G P ( x , y ) , Q ( x , y ) P(x,y),Q(x,y) P ( x , y ) , Q ( x , y ) G G G G G G 任意两点 A , B A,B A , B A A A B B B 任意两条曲线 C 1 , C 2 C_1,C_2 C 1 , C 2
∫ C 1 P d x + Q d y = ∫ C 2 P d x + Q d y \int_{C_1}P\mathrm d x+Q\mathrm d y=\int_{C_2} P\mathrm d x+Q\mathrm d y
∫ C 1 P d x + Q d y = ∫ C 2 P d x + Q d y
称为曲线积分在 G G G 与路径无关 。
沿任意一条封闭曲线上的积分值为零。也就是对于 ∀ C , ∮ C P d x + Q d y = 0 \forall C,\displaystyle \oint_C P\mathrm d x+Q\mathrm d y=0 ∀ C , ∮ C P d x + Q d y = 0
证明:令 C = C 1 + ∪ C 2 − C=C_1^+ \cup C_2^- C = C 1 + ∪ C 2 − ∫ C 1 + = ∫ C 2 + ⇒ ∫ C 1 + + ∫ C 2 − = 0 \displaystyle \int_{C_1^+}=\int_{C_2^+} \Rightarrow \int_{C_1^+}+\int_{C_2^-}=0 ∫ C 1 + = ∫ C 2 + ⇒ ∫ C 1 + + ∫ C 2 − = 0 ∮ C 1 + + C 2 − = 0 \displaystyle \oint_{C_1^++C_2^-}=0 ∮ C 1 + + C 2 − = 0
单连通域 设 D D D D D D D D D D D D 相当于区域内部没有空洞。
等价条件2:和格林公式的关系 设开区域 G G G P ( x , y ) , Q ( x , y ) P(x,y),Q(x,y) P ( x , y ) , Q ( x , y ) G G G 连续的偏导数 ,则曲线积分
∫ C P d x + Q d y \int_C P\mathrm d x+Q\mathrm d y
∫ C P d x + Q d y
在 G G G ∂ Q ∂ x = ∂ P ∂ y \displaystyle \frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y} ∂ x ∂ Q = ∂ y ∂ P G G G
反向证明:
∮ C P d x + Q d y = ∬ D 1 ( ∂ Q ∂ x − ∂ P ∂ x ) d x d y = 0 \oint _C P\mathrm d x+Q\mathrm d y=\iint_{D_1}\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial x}\right)\mathrm d x\mathrm d y=0
∮ C P d x + Q d y = ∬ D 1 ( ∂ x ∂ Q − ∂ x ∂ P ) d x d y = 0
因此无关。
正向证明:
如果不等于,假设大于。存在 M 0 M_0 M 0 U ( M 0 ) U(M_0) U ( M 0 )
( ∂ Q ∂ x − ∂ P ∂ y ) ∣ U ( M 0 ) > 0 \left.\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\right|_{U(M_0)}>0
( ∂ x ∂ Q − ∂ y ∂ P ) ∣ ∣ ∣ ∣ U ( M 0 ) > 0
设这个邻域的边界曲线为 K K K
等价条件3:和全微分的关系
设开区域 G G G P ( x , y ) , Q ( x , y ) P(x,y),Q(x,y) P ( x , y ) , Q ( x , y ) G G G P ( x , y ) d x + Q ( x , y ) d y P(x,y)\mathrm d x+Q(x,y)\mathrm d y P ( x , y ) d x + Q ( x , y ) d y G G G u ( x , y ) u(x,y) u ( x , y ) 全微分 的充分必要条件是:
∂ Q ∂ x = ∂ P ∂ y \frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y}
∂ x ∂ Q = ∂ y ∂ P
在 G G G
先证明正向。若 P ( x , y ) d x + Q ( x , y ) d y = d u ( x , y ) P(x,y)\mathrm{d} x+Q(x,y)\mathrm{d} y=\mathrm{d} u(x,y) P ( x , y ) d x + Q ( x , y ) d y = d u ( x , y ) ∂ Q ∂ x = ∂ 2 u ∂ y ∂ x = ∂ 2 u ∂ x ∂ y = ∂ P ∂ y \displaystyle \frac{\partial Q}{\partial x}=\frac{\partial^2 u}{\partial y\partial x}=\frac{\partial^2 u}{\partial x\partial y}=\frac{\partial P}{\partial y} ∂ x ∂ Q = ∂ y ∂ x ∂ 2 u = ∂ x ∂ y ∂ 2 u = ∂ y ∂ P
再证明反向,若 ∂ Q ∂ x = ∂ P ∂ y \displaystyle \frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y} ∂ x ∂ Q = ∂ y ∂ P ∫ C P d x + Q d y \displaystyle \int_C P\mathrm{d} x+Q\mathrm{d} y ∫ C P d x + Q d y
构造 u ( x , y ) = ∫ ( x 0 , y 0 ) ( x , y ) P ( x , y ) d x + Q ( x , y ) d y u(x,y)=\displaystyle \int_{(x_0,y_0)}^{(x,y)} P(x,y)\mathrm{d} x+Q(x,y)\mathrm{d} y u ( x , y ) = ∫ ( x 0 , y 0 ) ( x , y ) P ( x , y ) d x + Q ( x , y ) d y
那么如何求原函数 u ( x , y ) u(x,y) u ( x , y ) u ( x , y ) = ∫ ( 0 , 0 ) ( x , y ) P d x + Q d y \displaystyle u(x,y)=\int_{(0,0)}^{(x,y)} P \mathrm{d} x+Q\mathrm{d} y u ( x , y ) = ∫ ( 0 , 0 ) ( x , y ) P d x + Q d y u ( x , y ) u(x,y) u ( x , y ) u ( x , y ) = ∫ P ( x , y ) d x + C 1 ( y ) = ∫ Q ( x , y ) d y + C 2 ( x ) \displaystyle u(x,y)=\int P(x,y) \mathrm{d} x+C_1 (y)=\int Q(x,y)\mathrm{d} y+C_2(x) u ( x , y ) = ∫ P ( x , y ) d x + C 1 ( y ) = ∫ Q ( x , y ) d y + C 2 ( x )
等价条件 4:∫ C P d x + Q d y \displaystyle \int_C P\mathrm d x+Q\mathrm d y ∫ C P d x + Q d y
例题5 设函数 P ( x , y ) P(x,y) P ( x , y ) x o y xoy x o y ∫ C P ( x , y ) d x + 2 x y d y \displaystyle \int_C P(x,y) \mathrm{d} x+2xy \mathrm{d} y ∫ C P ( x , y ) d x + 2 x y d y t t t ∫ ( 0 , 0 ) ( t , 1 ) P ( x , y ) d x + 2 x y d y = ∫ ( 0 , 0 ) ( 1 , t ) P ( x , y ) d x + 2 x y d y \displaystyle \int_{(0,0)}^{(t,1)} P(x,y)\mathrm{d} x+2xy\mathrm{d} y=\int_{(0,0)}^{(1,t)} P(x,y)\mathrm{d} x+2xy\mathrm{d} y ∫ ( 0 , 0 ) ( t , 1 ) P ( x , y ) d x + 2 x y d y = ∫ ( 0 , 0 ) ( 1 , t ) P ( x , y ) d x + 2 x y d y P ( x , y ) P(x,y) P ( x , y )
方法1 :由曲线积分和路径无关知道存在原函数 u ( x , y ) = x y 2 + C ( x ) u(x,y)=xy^2+C(x) u ( x , y ) = x y 2 + C ( x ) u ( t , 1 ) = u ( 1 , t ) u(t,1)=u(1,t) u ( t , 1 ) = u ( 1 , t ) C ( t ) = t 2 − t + C ( 1 ) C(t)=t^2-t+C(1) C ( t ) = t 2 − t + C ( 1 ) x x x P ( x , y ) = y 2 + 2 x − 1 P(x,y)=y^2+2x-1 P ( x , y ) = y 2 + 2 x − 1
方法2 :转化题目条件的路径为竖直路径和水平路径。
等价条件 5:梯度 设开区域 G G G P ( x , y ) , Q ( x , y ) P(x,y),Q(x,y) P ( x , y ) , Q ( x , y ) G G G ∫ C P d x + Q d y \displaystyle \int_C P\mathrm d x+Q\mathrm d y ∫ C P d x + Q d y G G G
P ( x , y ) i + Q ( x , y ) j P(x,y)\boldsymbol i+Q(x,y)\boldsymbol j
P ( x , y ) i + Q ( x , y ) j
是某个函数 u ( x , y ) u(x,y) u ( x , y ) 梯度 。
若积分区域 G G G C 1 C_1 C 1 C 2 C_2 C 2
∮ C 1 P d x + Q d y = ∮ C 2 P d x + Q d y \oint_{C_1} P \mathrm d x+Q\mathrm d y=\oint_{C_2} P\mathrm d x+Q\mathrm d y
∮ C 1 P d x + Q d y = ∮ C 2 P d x + Q d y



如果微分方程 P ( x , y ) d x + Q ( x , y ) d y = 0 P(x,y)\mathrm d x+Q(x,y)\mathrm d y=0 P ( x , y ) d x + Q ( x , y ) d y = 0 U U U
d U = P ( x , y ) d x + Q ( x , y ) d y = 0 \mathrm d U=P(x,y)\mathrm d x+Q(x,y)\mathrm d y=0
d U = P ( x , y ) d x + Q ( x , y ) d y = 0
则称为 全微分方程 。充要条件是 ∂ Q ∂ x − ∂ P ∂ y = 0 \displaystyle \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}=0 ∂ x ∂ Q − ∂ y ∂ P = 0
若 P ( x , y ) d x + Q ( x , y ) d y = 0 P(x,y)\mathrm d x+Q(x,y)\mathrm d y=0 P ( x , y ) d x + Q ( x , y ) d y = 0 μ ( x , y ) ⋅ [ P ( x , y ) d x + Q ( x , y ) d y ] = 0 \mu(x,y)\cdot [P(x,y)\mathrm d x+Q(x,y)\mathrm d y]=0 μ ( x , y ) ⋅ [ P ( x , y ) d x + Q ( x , y ) d y ] = 0 μ ( x , y ) \mu(x,y) μ ( x , y ) 积分因子 。
如何找到恰当的 积分因子 ?得到
∂ Q μ ∂ x − ∂ P μ ∂ y = 0 \frac{\partial Q\mu}{\partial x}-\frac{\partial P\mu}{\partial y}=0
∂ x ∂ Q μ − ∂ y ∂ P μ = 0
目标变为求解偏微分方程?只用找一个积分因子。不妨假设 μ \mu μ x x x
d μ d x Q + μ ∂ Q ∂ x = μ ∂ P ∂ y ⇒ d μ d x Q = − μ ( − ∂ P ∂ y + ∂ Q ∂ x ⏟ M ) \frac{\mathrm d \mu}{\mathrm d x}Q+\mu \frac{\partial Q}{\partial x}=\mu \frac{\partial P}{\partial y} \Rightarrow \frac{\mathrm d \mu}{\mathrm d x}Q=-\mu\left(\underbrace{-\frac{\partial P}{\partial y}+ \frac{\partial Q}{\partial x}}_{M}\right)
d x d μ Q + μ ∂ x ∂ Q = μ ∂ y ∂ P ⇒ d x d μ Q = − μ ⎝ ⎜ ⎜ ⎛ M − ∂ y ∂ P + ∂ x ∂ Q ⎠ ⎟ ⎟ ⎞
如果 M / Q M/Q M / Q x x x N ( x ) N(x) N ( x )
d μ μ = − N ( x ) d x ⇒ μ = e − ∫ M Q d x \frac{\mathrm d \mu}{\mu}=-N(x)\mathrm d x \Rightarrow \mu=e^{-\int \frac{M}{Q}\mathrm d x}
μ d μ = − N ( x ) d x ⇒ μ = e − ∫ Q M d x
求微分方程 ( y 2 + x y 2 + 2 y ) d x + 2 ( 1 + x y ) d y = 0 (y^2+xy^2+2y)\mathrm d x+2(1+xy)\mathrm d y=0 ( y 2 + x y 2 + 2 y ) d x + 2 ( 1 + x y ) d y = 0
P = y 2 + x y 2 + 2 y , Q = 2 ( 1 + x y ) , M = − ( 2 x y + 2 ) P=y^2+xy^2+2y,Q=2(1+xy),M=-(2xy+2) P = y 2 + x y 2 + 2 y , Q = 2 ( 1 + x y ) , M = − ( 2 x y + 2 ) M / Q M/Q M / Q
因此
μ = e x \mu=e^x
μ = e x
这样凑出来:
e x ( y 2 + x y 2 + 2 y ) d x + e x 2 ( 1 + x y ) d y = 0 e^x(y^2+xy^2+2y)\mathrm d x+e^x 2(1+xy)\mathrm d y=0
e x ( y 2 + x y 2 + 2 y ) d x + e x 2 ( 1 + x y ) d y = 0
怎么进行凑微分?
法一:全部拆开来
2 y e x d x + x y 2 e x d x + 2 e x d y + 2 x y e x d y = 0 2ye^x \mathrm d x+xy^2 e^x \mathrm d x+2e^x \mathrm d y+2xy e^x \mathrm d y=0
2 y e x d x + x y 2 e x d x + 2 e x d y + 2 x y e x d y = 0
2 d ( e x y ) + x d ( e x y 2 ) + e x y 2 d x = 0 2 \mathrm d (e^x y)+x \mathrm d (e^x y^2)+e^x y^2 \mathrm d x=0
2 d ( e x y ) + x d ( e x y 2 ) + e x y 2 d x = 0
d ( 2 e x y + x e x y 2 ) = 0 \mathrm d (2e^x y+xe^x y^2)=0
d ( 2 e x y + x e x y 2 ) = 0
法二:积分+微分
∫ e x 2 ( 1 + x y ) d y = e x 2 ( y + x y 2 ) + C ( x ) \int e^x 2(1+xy) \mathrm d y=e^x2(y+xy^2)+C(x)
∫ e x 2 ( 1 + x y ) d y = e x 2 ( y + x y 2 ) + C ( x )
e x ( 2 y + x y 2 + y 2 ) + C ′ ( x ) = e x ( 2 y + x y 2 + y 2 ) ⇒ C ′ ( x ) = 0 e^x(2y+xy^2+y^2)+C'(x)=e^x(2y+xy^2+y^2) \Rightarrow C'(x)=0
e x ( 2 y + x y 2 + y 2 ) + C ′ ( x ) = e x ( 2 y + x y 2 + y 2 ) ⇒ C ′ ( x ) = 0
法三:不使用积分因子的方法
先部分用凑全微分,得到
d ( x y 2 + 2 y ) + ( x y 2 + 2 y ) d x = 0 \mathrm d (xy^2+2y)+(xy^2+2y)\mathrm d x=0
d ( x y 2 + 2 y ) + ( x y 2 + 2 y ) d x = 0
得到
ln ∣ x y 2 + 2 x ∣ + x = 0 \ln |xy^2+2x|+x=0
ln ∣ x y 2 + 2 x ∣ + x = 0
熟悉 d ( x y ) , d ( x / y ) \mathrm d (xy),\mathrm d (x/y) d ( x y ) , d ( x / y )
y d x − x d y y 2 = d ( x y ) y d x − x d y x 2 = d ( − y x ) y d x − x d y x 2 + y 2 = d ( arctan x y ) y d x − x d y x y = d ( ln ∣ x y ∣ ) \frac{y\mathrm d x-x\mathrm d y}{y^2}=\mathrm d \left(\frac{x}{y}\right)\\
\frac{y\mathrm d x-x\mathrm d y}{x^2}=\mathrm d \left(-\frac{y}{x}\right)\\
\frac{y\mathrm d x-x\mathrm d y}{x^2+y^2}=\mathrm d \left(\arctan \frac{x}{y}\right)\\
\frac{y\mathrm d x-x\mathrm d y}{xy}=\mathrm d \left(\ln \left|\frac{x}{y}\right|\right)
y 2 y d x − x d y = d ( y x ) x 2 y d x − x d y = d ( − x y ) x 2 + y 2 y d x − x d y = d ( arctan y x ) x y y d x − x d y = d ( ln ∣ ∣ ∣ ∣ y x ∣ ∣ ∣ ∣ )
设开区域 G G G
曲线积分 ∫ C P d x + Q d y \displaystyle \int_C P\mathrm{d} x+Q\mathrm{d} y ∫ C P d x + Q d y
对于任意封闭曲线 C ∈ G C\in G C ∈ G ∮ C P d x + Q d y = 0 \displaystyle \oint_C P\mathrm{d} x+Q\mathrm{d} y=0 ∮ C P d x + Q d y = 0
∂ Q ∂ x − ∂ P ∂ y = 0 \displaystyle \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}=0 ∂ x ∂ Q − ∂ y ∂ P = 0 G G G P d x + Q d y = d u P\mathrm{d} x+Q\mathrm{d} y=\mathrm{d} u P d x + Q d y = d u P d x + Q d y = 0 P\mathrm{d} x+Q\mathrm{d} y=0 P d x + Q d y = 0 P i + Q j = ∇ u P\boldsymbol i+Q\boldsymbol j=\nabla u P i + Q j = ∇ u
一开始直接代入曲线、曲面的表达式。注意曲线内部不满足曲线方程。
如果是 ∫ A B φ ( x ) d x \displaystyle\int_A^B \varphi(x)\mathrm{d} x ∫ A B φ ( x ) d x
如果是一个函数 u ( x , y ) u(x,y) u ( x , y ) u ( B ) − u ( A ) u(B)-u(A) u ( B ) − u ( A ) A A A B B B
如果格林公式表示是 0,可以改变路径,不过要注意原路径和新路径之间不能围着奇点。注意路径是从哪一端趋近的。注意圆周方向顺时针还是逆时针。

∫ A B x d y = − ∫ A B y d x = S \displaystyle \int_A^B x\mathrm d y=-\int_A^B y\mathrm d x=S ∫ A B x d y = − ∫ A B y d x = S
不能直接利用对称性。

引例 Σ \Sigma Σ ρ ( x , y , z ) \rho(x,y,z) ρ ( x , y , z )
分割:把曲面任意分割成 n n n
取值(近似):在第 i i i ( ξ i , η i , ς i ) (\xi_i,\eta_i,\varsigma_i) ( ξ i , η i , ς i ) Δ m i ≈ ρ ( ξ i , η i , ς i ) ⋅ Δ S i \Delta m_i\approx \rho(\xi_i,\eta_i,\varsigma_i)\cdot \Delta S_i Δ m i ≈ ρ ( ξ i , η i , ς i ) ⋅ Δ S i Δ S i , d i \Delta S_i,d_i Δ S i , d i i = 1 , 2 , ⋯ , n i=1,2,\cdots,n i = 1 , 2 , ⋯ , n
求和:曲面 Σ \Sigma Σ m ≈ ∑ i = 1 n ρ ( ξ i , η i , ς i ) Δ S i \displaystyle m\approx \sum_{i=1}^n \rho(\xi_i,\eta_i,\varsigma_i)\Delta S_i m ≈ i = 1 ∑ n ρ ( ξ i , η i , ς i ) Δ S i
求极限:当 λ = max 1 ≤ i ≤ n { d i } → 0 \displaystyle \lambda=\max_{1\le i\le n}\{d_i\}\to 0 λ = 1 ≤ i ≤ n max { d i } → 0 m = lim λ → 0 ∑ i = 1 n ρ ( ξ i , η i , ς i ) Δ S i \displaystyle m=\lim_{\lambda \to 0}\sum_{i=1}^n \rho(\xi_i,\eta_i,\varsigma_i)\Delta S_i m = λ → 0 lim i = 1 ∑ n ρ ( ξ i , η i , ς i ) Δ S i
定义: 设 f ( x , y , z ) f(x, y, z) f ( x , y , z ) Σ \Sigma Σ Σ \Sigma Σ n n n i i i Δ Σ i \Delta \Sigma_i Δ Σ i Δ S i \Delta S_i Δ S i Δ Σ i \Delta \Sigma_i Δ Σ i ( ξ i , η i , φ i ) \left(\xi_i, \eta_i, \varphi_i\right) ( ξ i , η i , φ i ) d i d_i d i Δ Σ i \Delta \Sigma_i Δ Σ i ( i = 1 , 2 , ⋯ , n ) (i=1,2, \cdots, n) ( i = 1 , 2 , ⋯ , n ) λ = max 1 ≤ i ≤ n { d i } → 0 \displaystyle \lambda=\max _{1 \leq i \leq n}\left\{d_i\right\} \rightarrow 0 λ = 1 ≤ i ≤ n max { d i } → 0 ∑ i = 1 n f ( ξ i , η i , ς i ) Δ S i \displaystyle \sum_{i=1}^n f\left(\xi_i, \eta_i, \varsigma_i\right) \Delta S_i i = 1 ∑ n f ( ξ i , η i , ς i ) Δ S i I I I I I I f ( x , y , z ) f(x, y, z) f ( x , y , z ) Σ \Sigma Σ ∬ Σ f ( x , y , z ) d S \displaystyle \iint_{\Sigma} f(x, y, z) \mathrm{d} S ∬ Σ f ( x , y , z ) d S
性质相似,也有线性性质和积分区域可加性。d S \mathrm d S d S
当 f ( x , y , z ) ≡ 1 f(x,y,z)\equiv 1 f ( x , y , z ) ≡ 1 ∬ Σ d S = S Σ \displaystyle \iint_\Sigma \mathrm{d} S=S_\Sigma ∬ Σ d S = S Σ S Σ S_\Sigma S Σ
设函数 f ( x , y , z ) f(x,y,z) f ( x , y , z ) Σ \Sigma Σ Σ \Sigma Σ z = z ( x , y ) z=z(x,y) z = z ( x , y ) Σ \Sigma Σ x o y xoy x o y D x y D_{xy} D x y z ( x , y ) z(x,y) z ( x , y ) D x y D_{xy} D x y d S = 1 + z x 2 + z y 2 d x d y \mathrm d S=\sqrt{1+z_x^2+z_y^2}\mathrm d x\mathrm d y d S = 1 + z x 2 + z y 2 d x d y
∬ Σ f ( x , y , z ) d S = ∬ D x y f [ x , y , z ( x , y ) ] ⋅ 1 + z x 2 + z y 2 d x d y \boxed{\iint_\Sigma f(x,y,z){\color{blue}\mathrm d S}=\iint_{D_{xy}} f[x,y,z(x,y)]\cdot {\color{blue}\sqrt{1+z_x^2+z_y^2}\mathrm d x\mathrm d y}}
∬ Σ f ( x , y , z ) d S = ∬ D x y f [ x , y , z ( x , y ) ] ⋅ 1 + z x 2 + z y 2 d x d y
三个要点:曲面方程 z ( x , y ) z(x,y) z ( x , y ) D x y D_{xy} D x y d S = 1 + z x 2 + z y 2 d x d y \mathrm d S=\sqrt{1+z_x^2+z_y^2}\mathrm d x\mathrm d y d S = 1 + z x 2 + z y 2 d x d y
类似地,
∬ Σ f ( x , y , z ) d S = ∬ D y z f [ x ( y , z ) , y , z ] ⋅ 1 + x y 2 + x z 2 d y d z \boxed{\iint_{\Sigma} f(x,y,z)\mathrm d S=\iint_{D_{yz}} f[x(y,z),y,z]\cdot \sqrt{1+x_y^2+x_z^2}\mathrm d y\mathrm d z}
∬ Σ f ( x , y , z ) d S = ∬ D y z f [ x ( y , z ) , y , z ] ⋅ 1 + x y 2 + x z 2 d y d z
双参数方程
当曲面 Σ \Sigma Σ { x = x ( u , v ) y = y ( u , v ) z = z ( u , v ) \left\{\begin{aligned}x=x(u,v)\\y=y(u,v)\\z=z(u,v)\end{aligned}\right. ⎩ ⎪ ⎨ ⎪ ⎧ x = x ( u , v ) y = y ( u , v ) z = z ( u , v ) f ( x , y , z ) f(x,y,z) f ( x , y , z ) Σ \Sigma Σ ( u , v ) ∈ D u v (u,v)\in D_{uv} ( u , v ) ∈ D u v
∬ Σ f ( x , y , z ) d S = ∬ D u v f [ x ( u , v ) , y ( u , v ) , z ( u , v ) ] ⋅ A 2 + B 2 + C 2 d u d v \boxed{\iint_{\Sigma} f(x,y,z){\color{blue}\mathrm d S}=\iint_{D_{uv}} f[x(u,v),y(u,v),z(u,v)]\cdot {\color{blue}\sqrt{A^2+B^2+C^2}\mathrm d u\mathrm d v}}
∬ Σ f ( x , y , z ) d S = ∬ D u v f [ x ( u , v ) , y ( u , v ) , z ( u , v ) ] ⋅ A 2 + B 2 + C 2 d u d v
其中
A = ∂ ( y , z ) ∂ ( u , v ) , B = ∂ ( z , x ) ∂ ( u , v ) , C = ∂ ( x , y ) ∂ ( u , v ) , n = { A , B , C } A=\frac{\partial (y,z)}{\partial (u,v)},B=\frac{\partial (z,x)}{\partial (u,v)},C=\frac{\partial (x,y)}{\partial (u,v)},\boldsymbol n=\{A,B,C\}
A = ∂ ( u , v ) ∂ ( y , z ) , B = ∂ ( u , v ) ∂ ( z , x ) , C = ∂ ( u , v ) ∂ ( x , y ) , n = { A , B , C }

z = a 2 − x 2 − y 2 z x = − x a 2 − x 2 − y 2 , z y = − y a 2 − x 2 − y 2 球 面 的 面 积 元 素 : d S = a a 2 − x 2 − y 2 d x d y z=\sqrt{a^2-x^2-y^2}\\
z_x=\frac{-x}{\sqrt{a^2-x^2-y^2}},z_y=\frac{-y}{\sqrt{a^2-x^2-y^2}}\\
球面的面积元素:\mathrm d S=\frac{a}{\sqrt{a^2-x^2-y^2}}\mathrm d x\mathrm d y
z = a 2 − x 2 − y 2 z x = a 2 − x 2 − y 2 − x , z y = a 2 − x 2 − y 2 − y 球 面 的 面 积 元 素 : d S = a 2 − x 2 − y 2 a d x d y
因此
\iint_\Sigma\frac{1}{z}\mathrm{d} S=\int_0^{2\pi }\mathrm{d} \theta \int_0^\sqrt{a^2-h^2} \frac{a}{a^2-r^2} \cdot r \mathrm{d} r=2\pi a \ln \frac{a}{h}





设曲面 Σ : x 2 + y 2 + z 2 = 4 \Sigma: x^2+y^2+z^2=4 Σ : x 2 + y 2 + z 2 = 4
∯ Σ ( 3 x − 2 y − x z + z 2 ) d S \oiint_\Sigma (3x-2y-xz+z^2)\mathrm d S
∬ Σ ( 3 x − 2 y − x z + z 2 ) d S
其中类似于 x n y m x^ny^m x n y m
1 3 ∯ Σ ( x 2 + y 2 + z 2 ) d S \frac{1}{3}\oiint_\Sigma (x^2+y^2+z^2)\mathrm d S
3 1 ∬ Σ ( x 2 + y 2 + z 2 ) d S
已知曲面 Σ : { ( x , y , z ) : x + y + z = 1 , x ≥ 0 , y ≥ 0 , z ≥ 0 } \Sigma:\{(x,y,z):x+y+z=1,x\ge 0,y\ge 0,z\ge 0\} Σ : { ( x , y , z ) : x + y + z = 1 , x ≥ 0 , y ≥ 0 , z ≥ 0 } ∫ Σ ( 2 π x + 5 y 2 ) d S \displaystyle \int _\Sigma (2\pi x+5y^2)\mathrm d S ∫ Σ ( 2 π x + 5 y 2 ) d S
曲面的侧 设 Σ \Sigma Σ M ( x , y , z ) M(x,y,z) M ( x , y , z ) Σ \Sigma Σ M M M n \boldsymbol n n − n -\boldsymbol n − n M M M Σ \Sigma Σ n \boldsymbol n n
这里主要讨论双侧曲面。把指定了侧的曲面 Σ \Sigma Σ Σ \Sigma Σ Σ + \Sigma^+ Σ + Σ \Sigma Σ Σ − \Sigma^- Σ −
引例
v = P ( x , y , z ) i + Q ( x , y , z ) j + R ( x , y , z ) k \boldsymbol v=P(x,y,z)\boldsymbol i+Q(x,y,z)\boldsymbol j+R(x,y,z)\boldsymbol k
v = P ( x , y , z ) i + Q ( x , y , z ) j + R ( x , y , z ) k
Σ \Sigma Σ P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) P(x,y,z),Q(x,y,z),R(x,y,z) P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) Σ \Sigma Σ Φ \Phi Φ
利用元素法:在 Σ \Sigma Σ M M M d S \mathrm d S d S v \boldsymbol v v n 0 \boldsymbol n^0 n 0
d Φ = ( v ⋅ n 0 ) d S \mathrm d \Phi=(\boldsymbol v\cdot \boldsymbol n^0)\mathrm d S
d Φ = ( v ⋅ n 0 ) d S
Φ = ∬ Σ ( v ⋅ n 0 ) d S \Phi=\iint_\Sigma (\boldsymbol v\cdot \boldsymbol n^0)\mathrm d S
Φ = ∬ Σ ( v ⋅ n 0 ) d S
设 n 0 = { cos α , cos β , cos γ } \boldsymbol n^0=\left\{\cos\alpha,\cos\beta,\cos\gamma \right\} n 0 = { cos α , cos β , cos γ } d S = n 0 d S \color{red}\mathrm d \boldsymbol S=\boldsymbol n^0\mathrm d S d S = n 0 d S
d S = { cos α d S , cos β d S , cos γ d S } = { d y d z , d z d x , d x d y } \mathrm d \boldsymbol S=\left\{\cos \alpha\mathrm d S,\cos \beta\mathrm d S,\cos \gamma \mathrm d S\right\}=\{\mathrm d y\mathrm d z,\mathrm d z\mathrm d x,\mathrm d x\mathrm d y\}
d S = { cos α d S , cos β d S , cos γ d S } = { d y d z , d z d x , d x d y }
Φ = ∬ Σ v ⋅ d S = ∬ Σ P ( x , y , z ) d y d z + Q ( x , y , z ) d x d z + R ( x , y , z ) d y d x \Phi=\iint_\Sigma \boldsymbol v \cdot \mathrm{d} \boldsymbol S=\iint_\Sigma P(x,y,z)\mathrm d y\mathrm d z+Q(x,y,z)\mathrm d x\mathrm d z+R(x,y,z)\mathrm d y\mathrm d x
Φ = ∬ Σ v ⋅ d S = ∬ Σ P ( x , y , z ) d y d z + Q ( x , y , z ) d x d z + R ( x , y , z ) d y d x
设 Σ \Sigma Σ R ( x , y , z ) R(x,y,z) R ( x , y , z ) Σ \Sigma Σ Σ \Sigma Σ n n n i i i Δ Σ i \Delta \Sigma_i Δ Σ i Δ Σ i \Delta \Sigma_i Δ Σ i x o y xoy x o y ( Δ σ i ) x y (\Delta \sigma_i)_{xy} ( Δ σ i ) x y Δ Σ i \Delta \Sigma_i Δ Σ i ( ξ i , η i , ς i ) (\xi_i,\eta_i,\varsigma_i) ( ξ i , η i , ς i ) d i d_i d i Δ Σ i \Delta \Sigma_i Δ Σ i i = 1 , 2 , ⋯ , n i=1,2,\cdots,n i = 1 , 2 , ⋯ , n λ = max 1 ≤ i ≤ n { d i } → 0 \displaystyle \lambda = \max_{1\le i\le n} \{d_i\}\to 0 λ = 1 ≤ i ≤ n max { d i } → 0
∬ Σ R ( x , y , z ) d x d y = lim λ → 0 ∑ i = 1 n R ( ξ i , η i , ς i ) ( Δ σ i ) x y \iint_\Sigma R(x,y,z)\mathrm d x\mathrm d y=\lim_{\lambda \to 0}\sum_{i=1}^n R(\xi_i,\eta_i,\varsigma_i)(\Delta \sigma_i)_{xy}
∬ Σ R ( x , y , z ) d x d y = λ → 0 lim i = 1 ∑ n R ( ξ i , η i , ς i ) ( Δ σ i ) x y
特殊性质,当曲面方向相反时:
∬ Σ − P d y d z + Q d z d x + R d x d y = − ∬ Σ P d y d z + Q d z d x + R d x d y \iint_{\Sigma^-} P\mathrm d y\mathrm d z+Q\mathrm d z\mathrm d x+R\mathrm d x\mathrm d y=-\iint_{\Sigma} P\mathrm d y\mathrm d z+Q\mathrm d z\mathrm d x+R\mathrm d x\mathrm d y
∬ Σ − P d y d z + Q d z d x + R d x d y = − ∬ Σ P d y d z + Q d z d x + R d x d y


上侧:
∬ Σ R ( x , y , z ) d x d y = ∬ D x y R [ x , y , z ( x , y ) ] d x d y \iint_\Sigma R(x,y,z)\mathrm d x\mathrm d y=\iint_{D_{xy}} R[x,y,z(x,y)]\mathrm d x\mathrm d y
∬ Σ R ( x , y , z ) d x d y = ∬ D x y R [ x , y , z ( x , y ) ] d x d y
下侧:
∬ Σ R ( x , y , z ) d x d y = − ∬ D x y R [ x , y , z ( x , y ) ] d x d y \iint_\Sigma R(x,y,z)\mathrm d x\mathrm d y=-\iint_{D_{xy}} R[x,y,z(x,y)]\mathrm d x\mathrm d y
∬ Σ R ( x , y , z ) d x d y = − ∬ D x y R [ x , y , z ( x , y ) ] d x d y


第二类曲面积分一般不考虑对称性。


检查是否符合轮换性。为什么符合轮换性,轮换改变积分区域的表达式,结果不变。

对于平面 Σ 1 : z = 1 \Sigma_1:z=1 Σ 1 : z = 1 x o y xoy x o y D 1 : x 2 + y 2 ≤ 1 D_1:x^2+y^2 \le 1 D 1 : x 2 + y 2 ≤ 1
I = − ∬ D 1 e x 2 + y 2 d x d y = − e ∫ 0 2 π d θ ∫ 0 1 1 r ⋅ r d r = − 2 π e I=-\iint_{D_1} \frac{e}{\sqrt{x^2+y^2}}\mathrm{d} x\mathrm{d} y=-e \int_0^{2\pi} \mathrm{d} \theta \int_0^1 \frac{1}{r}\cdot r \mathrm{d} r=-2\pi e
I = − ∬ D 1 x 2 + y 2 e d x d y = − e ∫ 0 2 π d θ ∫ 0 1 r 1 ⋅ r d r = − 2 π e
对于平面 Σ 2 : z = 2 \Sigma_2:z=2 Σ 2 : z = 2 x o y xoy x o y D 2 : x 2 + y 2 ≤ 4 D_2:x^2+y^2\le 4 D 2 : x 2 + y 2 ≤ 4
I = ∬ D 2 e 2 x 2 + y 2 d x d y = e 2 ∫ 0 2 π d θ ∫ 0 2 1 r ⋅ r d r = 4 π e 2 I=\iint_{D_2} \frac{e^2}{\sqrt{x^2+y^2}} \mathrm{d} x\mathrm{d} y=e^2 \int_0^{2\pi} \mathrm{d} \theta \int_0^2 \frac{1}{r} \cdot r\mathrm{d}r=4\pi e^2
I = ∬ D 2 x 2 + y 2 e 2 d x d y = e 2 ∫ 0 2 π d θ ∫ 0 2 r 1 ⋅ r d r = 4 π e 2
对于锥面 Σ 3 : z = x 2 + y 2 \Sigma_3:z=\sqrt{x^2+y^2} Σ 3 : z = x 2 + y 2 x o y xoy x o y D 3 : 1 ≤ x 2 + y 2 ≤ 4 D_3:1\le x^2+y^2 \le 4 D 3 : 1 ≤ x 2 + y 2 ≤ 4
I = − ∬ D 3 e x 2 + y 2 x 2 + y 2 d x d y = − ∫ 0 2 π d θ ∫ 1 2 e r r ⋅ r d r = − 2 π ( e 2 − e ) I=-\iint_{D_3} \frac{e^{\sqrt{x^2+y^2}}}{\sqrt{x^2+y^2}}\mathrm{d} x\mathrm{d} y=-\int_0^{2\pi}\mathrm{d} \theta \int_1^2 \frac{e^r}{r}\cdot r\mathrm{d} r=-2\pi(e^2-e)
I = − ∬ D 3 x 2 + y 2 e x 2 + y 2 d x d y = − ∫ 0 2 π d θ ∫ 1 2 r e r ⋅ r d r = − 2 π ( e 2 − e )
因此结果是三个数相加。
向量值函数 F ( x , y , z ) = P i + Q j + R k \boldsymbol F (x,y,z)=P\boldsymbol i+Q\boldsymbol j+R\boldsymbol k F ( x , y , z ) = P i + Q j + R k
∬ Σ F ( x , y , z ) d S = ( ± ) ∬ D u v ( P A + Q B + R C ) d u d v \iint_{\Sigma} \boldsymbol F(x,y,z)\mathrm d \boldsymbol S=(\pm)\iint_{D_{uv}} (PA+QB+RC)\mathrm d u\mathrm d v
∬ Σ F ( x , y , z ) d S = ( ± ) ∬ D u v ( P A + Q B + R C ) d u d v
其中 n = { A , B , C } \boldsymbol n=\{A,B,C\} n = { A , B , C }
A = ∂ ( y , z ) ∂ ( u , v ) , B = ∂ ( z , x ) ∂ ( u , v ) , C = ∂ ( x , y ) ∂ ( u , v ) A=\frac{\partial(y,z)}{\partial (u,v)},B=\frac{\partial(z,x)}{\partial (u,v)},C=\frac{\partial(x,y)}{\partial (u,v)}
A = ∂ ( u , v ) ∂ ( y , z ) , B = ∂ ( u , v ) ∂ ( z , x ) , C = ∂ ( u , v ) ∂ ( x , y )
合一投影法
当 z = z ( x , y ) z=z(x,y) z = z ( x , y ) A = − z x , B = − z y , C = 1 A=-z_x,B=-z_y,C=1 A = − z x , B = − z y , C = 1 n = { − z x , − z y , 1 } \boldsymbol n=\{-z_x,-z_y,1\} n = { − z x , − z y , 1 }
∬ Σ F ( x , y , z ) d S = ( ± ) ∬ D x y ( − P z x − Q z y + R ) d x d y = ( ± ) ∬ D x y ( F x F z ⋅ P + F y F z ⋅ Q + R ) d x d y \iint_{\Sigma} \boldsymbol F(x,y,z)\mathrm d \boldsymbol S=(\pm)\iint_{D_{xy}}(-Pz_x-Qz_y+R)\mathrm d x\mathrm d y\\=(\pm)\iint_{D_{xy}} \left(\frac{F_x}{F_z}\cdot P+\frac{F_y}{F_z} \cdot Q+R\right)\mathrm d x\mathrm d y
∬ Σ F ( x , y , z ) d S = ( ± ) ∬ D x y ( − P z x − Q z y + R ) d x d y = ( ± ) ∬ D x y ( F z F x ⋅ P + F z F y ⋅ Q + R ) d x d y
P.S. 如果 z z z

已知曲面积分 Σ : x 2 + y 2 + z 2 = 8 ( z ≥ 3 ) \Sigma:x^2+y^2+z^2=8(z\ge \sqrt{3}) Σ : x 2 + y 2 + z 2 = 8 ( z ≥ 3 )
∫ Σ 2 x y d y d z − y 2 d z d x + 5 z 2 d x d y \int_\Sigma 2xy\mathrm d y\mathrm d z-y^2 \mathrm d z\mathrm d x+5z^2 \mathrm d x \mathrm d y
∫ Σ 2 x y d y d z − y 2 d z d x + 5 z 2 d x d y
关键是利用 ( d y d z , d z d x , d x d y ) (\mathrm d y\mathrm d z,\mathrm d z\mathrm d x,\mathrm d x\mathrm d y) ( d y d z , d z d x , d x d y ) ∇ F \nabla F ∇ F
F x d y d z = F y d z d x = F z d x d y \frac{F_x}{\mathrm d y\mathrm d z}=\frac{F_y}{\mathrm d z\mathrm d x}=\frac{F_z}{\mathrm d x\mathrm d y}
d y d z F x = d z d x F y = d x d y F z
因此,转化为
∫ D x y ( 2 x y x z − y 2 y z + 5 z 2 ) d x d y \int_{D_{xy}}\left(2xy \frac{x}{z}-y^2 \frac{y}{z}+5z^2\right)\mathrm d x\mathrm d y
∫ D x y ( 2 x y z x − y 2 z y + 5 z 2 ) d x d y
其中 D x y : { x 2 + y 2 ≤ 5 } D_{xy}:\{x^2+y^2 \le 5\} D x y : { x 2 + y 2 ≤ 5 }
那就极坐标换元。看到积分区域,一定要想到 奇偶性 。

关键点:化成 x 2 + y 2 + z 2 − 2 x^2+y^2+z^2-2 x 2 + y 2 + z 2 − 2 轮换对称 。
∬ Σ F ( x , y , z ) d S = ∬ Σ P d y d z + Q d z d x + R d x d y = ∬ Σ ( P cos α + Q cos β + R cos γ ) d S = ∬ Σ ( F ⋅ n 0 ) d S \iint_{\Sigma} \boldsymbol F(x,y,z)\mathrm d \boldsymbol S=\iint_\Sigma P\mathrm{d} y\mathrm{d} z+Q\mathrm{d} z\mathrm{d} x+R\mathrm{d} x\mathrm{d} y\\=\iint_\Sigma (P\cos \alpha+Q\cos\beta+R\cos \gamma )\mathrm{d} S=\iint_{\Sigma}(\boldsymbol F\cdot \boldsymbol n^0)\mathrm d S
∬ Σ F ( x , y , z ) d S = ∬ Σ P d y d z + Q d z d x + R d x d y = ∬ Σ ( P cos α + Q cos β + R cos γ ) d S = ∬ Σ ( F ⋅ n 0 ) d S
封闭 曲面的 外侧 。
∯ ∂ V P d y d z + Q d z d x + R d x d y = ∭ Ω ( ∂ P ∂ x + ∂ Q ∂ y + ∂ R ∂ z ) d V \boxed{\oiint_{\partial V} P\mathrm d y\mathrm d z+Q\mathrm d z\mathrm d x+R\mathrm d x\mathrm d y=\iiint_{\Omega}\left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}\right)\mathrm d V }
∬ ∂ V P d y d z + Q d z d x + R d x d y = ∭ Ω ( ∂ x ∂ P + ∂ y ∂ Q + ∂ z ∂ R ) d V
如果 F = ( P , Q , R ) , n 0 d S = d S = ( d y d z , d z d x , d x d y ) \boldsymbol F=(P,Q,R),\boldsymbol n^0 \mathrm d S=\mathrm d \boldsymbol S=(\mathrm d y\mathrm d z,\mathrm d z\mathrm d x,\mathrm d x\mathrm d y) F = ( P , Q , R ) , n 0 d S = d S = ( d y d z , d z d x , d x d y )
高斯公式的向量形式 :
∯ Σ ( F ⋅ n 0 ) d S = ∭ Ω ( ∇ ⋅ F ) d V \oiint_{\Sigma} (\boldsymbol F\cdot \boldsymbol n^0)\mathrm d S=\iiint_{\Omega} (\nabla \cdot \boldsymbol F)\mathrm d V
∬ Σ ( F ⋅ n 0 ) d S = ∭ Ω ( ∇ ⋅ F ) d V
类似于 Green 公式,我们可以用高斯公式计算体积:
V = ∭ V d x d y d z = ∯ S + x d y d z = ∯ S + y d z d x = ∯ S + z d x d y = 1 3 ∯ S + ∑ c y c x d y d z V=\iiint_{V}\mathrm d x\mathrm d y\mathrm d z=\oiint_{S^+} x\mathrm d y\mathrm d z=\oiint_{S^+} y\mathrm d z\mathrm d x=\oiint_{S^+} z\mathrm d x\mathrm d y=\frac{1}{3}\oiint_{S^+} \sum_{\mathrm{cyc}}x\mathrm d y\mathrm d z
V = ∭ V d x d y d z = ∬ S + x d y d z = ∬ S + y d z d x = ∬ S + z d x d y = 3 1 ∬ S + c y c ∑ x d y d z


计算曲面积分
∬ Σ ( 6 y + 1 ) x d y d z + ( 1 − y 2 ) d z d x − 4 y z d x d y \iint_{\Sigma} (6y+1)x\mathrm d y\mathrm d z+(1-y^2)\mathrm d z\mathrm d x-4yz\mathrm d x\mathrm d y
∬ Σ ( 6 y + 1 ) x d y d z + ( 1 − y 2 ) d z d x − 4 y z d x d y
其中 Σ \Sigma Σ z = y − 1 , x = 0 ( 1 ≤ y ≤ 3 ) z=\sqrt{y-1},x=0(1\le y\le 3) z = y − 1 , x = 0 ( 1 ≤ y ≤ 3 ) y y y
如果用第二类曲面积分……
旋转曲面方程为 x 2 + z 2 = y − 1 ( 1 ≤ y ≤ 3 ) x^2+z^2=y-1 (1\le y \le3) x 2 + z 2 = y − 1 ( 1 ≤ y ≤ 3 )
再添加 Σ 1 : y = 3 \Sigma_1:y=3 Σ 1 : y = 3
∬ Σ + ∬ Σ 1 = ∯ Σ + Σ 1 = ∭ Ω d V = 2 π \iint_\Sigma+\iint_{\Sigma_1}=\oiint_{\Sigma+\Sigma_1}=\iiint_{\Omega} \mathrm d V=2\pi
∬ Σ + ∬ Σ 1 = ∬ Σ + Σ 1 = ∭ Ω d V = 2 π
再算 ∬ Σ 1 \displaystyle \iint_{\Sigma_1} ∬ Σ 1 d y = 0 \mathrm d y=0 d y = 0 y = 3 y=3 y = 3
∬ x 2 + z 2 ≤ 2 − 8 d z d x = − 16 π \iint_{x^2+z^2 \le 2} -8\mathrm d z\mathrm d x=-16\pi
∬ x 2 + z 2 ≤ 2 − 8 d z d x = − 1 6 π
故所求曲面积分= 2 π − ( − 16 π ) = 18 π =2\pi-(-16\pi)=18\pi = 2 π − ( − 1 6 π ) = 1 8 π
第二类曲面积分(合一投影法)也能做,不过比较繁琐。


直接计算的方便之处:有一项是0.

浮力用高斯公式计算:
∯ Σ ρ g z = ∭ Ω ρ g = ρ g V \oiint_{\Sigma} \rho g z=\iiint_{\Omega} \rho g=\rho g V
∬ Σ ρ g z = ∭ Ω ρ g = ρ g V
计算曲面积分 ∫ S x d y d z + y d z d x + z d x d y ( x 2 + 4 y 2 + 9 z 2 ) 3 / 2 \displaystyle \int_S \frac{x\mathrm d y\mathrm d z+y \mathrm d z\mathrm d x+z\mathrm d x\mathrm d y}{(x^2+4y^2+9z^2)^{3/2}} ∫ S ( x 2 + 4 y 2 + 9 z 2 ) 3 / 2 x d y d z + y d z d x + z d x d y
当曲面 S S S
∭ Ω ∂ P ∂ x + ∂ Q ∂ y + ∂ R ∂ z = 0 \iiint_\Omega \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}=0
∭ Ω ∂ x ∂ P + ∂ y ∂ Q + ∂ z ∂ R = 0
因此不含奇点,结果为 0.
当曲面 S S S x 2 + y 2 + z 2 = 1 x^2+y^2+z^2=1 x 2 + y 2 + z 2 = 1 x 2 + 4 y 2 + 9 z 2 = 1 x^2+4y^2+9z^2=1 x 2 + 4 y 2 + 9 z 2 = 1 X = x , Y = 2 y , Z = 3 z X=x,Y=2y,Z=3z X = x , Y = 2 y , Z = 3 z
∫ S 1 6 X d Y d Z + 1 6 Y d X d Z + 1 6 Z d X d Y = 1 2 ∫ S Z d X d Y = 1 2 × 2 ∬ D X Y Z d X d Y = 2 3 π \int_S \frac{1}{6}X\mathrm d Y\mathrm d Z+\frac{1}{6}Y\mathrm d X\mathrm d Z+\frac{1}{6}Z\mathrm d X\mathrm d Y=\frac{1}{2} \int_S Z\mathrm d X\mathrm d Y=\frac{1}{2}\times 2 \iint_{D_{XY}} Z\mathrm d X\mathrm d Y=\frac{2}{3}\pi
∫ S 6 1 X d Y d Z + 6 1 Y d X d Z + 6 1 Z d X d Y = 2 1 ∫ S Z d X d Y = 2 1 × 2 ∬ D X Y Z d X d Y = 3 2 π
设向量场由 F ( x , y , z ) = P ( x , y , z ) i + Q ( x , y , z ) j + R ( x , y , z ) k \boldsymbol F(x,y,z)=P(x,y,z)\boldsymbol i+Q(x,y,z)\boldsymbol j+R(x,y,z)\boldsymbol k F ( x , y , z ) = P ( x , y , z ) i + Q ( x , y , z ) j + R ( x , y , z ) k
Φ = ∬ Σ F ⋅ d S = ∬ Σ P d y d z + Q d z d x + R d x d y \Phi=\iint_{\Sigma} \boldsymbol F \cdot \mathrm d \boldsymbol S=\iint_{\Sigma} P\mathrm d y\mathrm d z+Q\mathrm d z\mathrm d x+R\mathrm d x\mathrm d y
Φ = ∬ Σ F ⋅ d S = ∬ Σ P d y d z + Q d z d x + R d x d y
Φ > 0 \Phi>0 Φ > 0 Σ \Sigma Σ
设向量场 F \boldsymbol F F M ( x , y , z ) M(x,y,z) M ( x , y , z ) M M M Σ \Sigma Σ Ω \Omega Ω Σ \Sigma Σ Δ V \Delta V Δ V Ω \Omega Ω Δ Φ \Delta \Phi Δ Φ Σ \Sigma Σ
lim Ω → M Δ Φ Δ V = lim Ω → M 1 Δ V ∯ Σ F ⋅ d S \lim_{\Omega \to M} \frac{\Delta \Phi}{\Delta V}=\lim_{\Omega \to M}\frac{1}{\Delta V} \oiint_{\Sigma} \boldsymbol F \cdot \mathrm d \boldsymbol S
Ω → M lim Δ V Δ Φ = Ω → M lim Δ V 1 ∬ Σ F ⋅ d S
存在,则称为向量场 F \boldsymbol F F M M M div F ∣ M \operatorname{div} \boldsymbol F|_{M} d i v F ∣ M
由高斯公式和三重积分中值定理可以得到
div F ∣ M = ∂ P ∂ x + ∂ Q ∂ y + ∂ R ∂ z \operatorname{div} \boldsymbol F|_{M}=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}
d i v F ∣ M = ∂ x ∂ P + ∂ y ∂ Q + ∂ z ∂ R
高斯公式又称散度公式
∯ Σ F ⋅ d S = ∭ Ω div F d V \oiint_\Sigma \boldsymbol F\cdot \mathrm d \boldsymbol S=\iiint_{\Omega}\operatorname{div} \boldsymbol F \mathrm d V
∬ Σ F ⋅ d S = ∭ Ω d i v F d V
设 Σ \Sigma Σ Γ \Gamma Γ F ⃗ = P i ⃗ + Q j ⃗ + R k → \vec{F}=P \vec{i}+Q \vec{j}+R \overrightarrow{\boldsymbol{k}} F = P i + Q j + R k Σ \Sigma Σ
∮ Γ P d x + Q d y + R d z = ∬ Σ ( ∂ R ∂ y − ∂ Q ∂ z ) d y d z + ( ∂ P ∂ z − ∂ R ∂ x ) d z d x + ( ∂ Q ∂ x − ∂ P ∂ y ) d x d y = ∬ Σ ∣ d y d z d z d x d x d y ∂ ∂ x ∂ ∂ y ∂ ∂ z P Q R ∣ \begin{aligned}
\left.\oint_{\Gamma} P \mathrm{~d} x+Q \mathrm{~d} y+R \mathrm{~d} z =\iint_{\Sigma}\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right) \mathrm{d} y \mathrm{~d} z+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right) \mathrm{d} z \mathrm{~d} x+(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \mathrm{d} x \mathrm{~d} y\\
=\iint_{\Sigma}\begin{vmatrix}
\mathrm d y\mathrm d z & \mathrm d z\mathrm d x &\mathrm d x\mathrm d y\\
\dfrac{\partial }{\partial x} & \dfrac{\partial }{\partial y} &\dfrac{\partial }{\partial z}\\
P&Q&R
\end{vmatrix}
\end{aligned}
∮ Γ P d x + Q d y + R d z = ∬ Σ ( ∂ y ∂ R − ∂ z ∂ Q ) d y d z + ( ∂ z ∂ P − ∂ x ∂ R ) d z d x + ( ∂ x ∂ Q − ∂ y ∂ P ) d x d y = ∬ Σ ∣ ∣ ∣ ∣ ∣ ∣ ∣ d y d z ∂ x ∂ P d z d x ∂ y ∂ Q d x d y ∂ z ∂ R ∣ ∣ ∣ ∣ ∣ ∣ ∣
其中曲线 Γ \Gamma Γ Σ \Sigma Σ
也就是旋度形式的格林公式:
∮ ∂ Σ + P d x + Q d y + R d z = ∬ D ( ∇ × F ) d S \oint_{\partial \Sigma ^+} P\mathrm d x+Q\mathrm d y+R\mathrm d z=\iint_D (\nabla \times \boldsymbol F)\mathrm d \boldsymbol S
∮ ∂ Σ + P d x + Q d y + R d z = ∬ D ( ∇ × F ) d S
格林公式:只有 d x d y \mathrm d x\mathrm d y d x d y d z = 0 \mathrm d z=0 d z = 0
公式(**)称为斯托克斯公式。
推广到三维的情况,积分与路径无关的条件是 ∇ × F = 0 \nabla \times \boldsymbol F=\boldsymbol 0 ∇ × F = 0
直接积分的情况:
∫ C f ( x ) d x + g ( y ) d y + h ( z ) d z \int_C f(x)\mathrm d x+g(y)\mathrm d y+h(z)\mathrm d z
∫ C f ( x ) d x + g ( y ) d y + h ( z ) d z
设向量场由 F ( x , y , z ) = P ( x , y , z ) i + Q ( x , y , z ) j + R ( x , y , z ) k \boldsymbol F(x,y,z)=P(x,y,z)\boldsymbol i+Q(x,y,z)\boldsymbol j+R(x,y,z)\boldsymbol k F ( x , y , z ) = P ( x , y , z ) i + Q ( x , y , z ) j + R ( x , y , z ) k
∫ Γ P d x + Q d y + R d z = ∫ Γ F ⋅ d r \int_\Gamma P\mathrm d x+Q\mathrm d y+R\mathrm d z=\int_{\Gamma} \boldsymbol F\cdot \mathrm d \boldsymbol r
∫ Γ P d x + Q d y + R d z = ∫ Γ F ⋅ d r
称为向量场 F \boldsymbol F F Γ \Gamma Γ
设 M ( x , y , z ) M(x,y,z) M ( x , y , z ) F \boldsymbol F F
∣ i j k ∂ ∂ x ∂ ∂ y ∂ ∂ z P Q R ∣ M = ( ∂ R ∂ y − ∂ Q ∂ z ) M i + ( ∂ P ∂ z − ∂ R ∂ x ) M j + ( ∂ Q ∂ x − ∂ P ∂ y ) M k \begin{vmatrix}
\boldsymbol i & \boldsymbol j &\boldsymbol k\\
\dfrac{\partial }{\partial x} & \dfrac{\partial }{\partial y} &\dfrac{\partial }{\partial z}\\
P&Q&R
\end{vmatrix}_M=\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right)_M \boldsymbol i+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right)_M \boldsymbol j+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)_M \boldsymbol k
∣ ∣ ∣ ∣ ∣ ∣ ∣ i ∂ x ∂ P j ∂ y ∂ Q k ∂ z ∂ R ∣ ∣ ∣ ∣ ∣ ∣ ∣ M = ( ∂ y ∂ R − ∂ z ∂ Q ) M i + ( ∂ z ∂ P − ∂ x ∂ R ) M j + ( ∂ x ∂ Q − ∂ y ∂ P ) M k
为向量场 F \boldsymbol F F M M M rot F \operatorname{rot} \boldsymbol F r o t F



引入线性映射
∑ i f i ( x 1 , x 2 ⋯ , x n ) d x i 1 d x i 2 ⋯ d x i m \sum_i f_i(x_1,x_2\cdots,x_n) \mathrm d x_{i_1} \mathrm d x_{i_2}\cdots\mathrm d x_{i_m}
i ∑ f i ( x 1 , x 2 ⋯ , x n ) d x i 1 d x i 2 ⋯ d x i m
其中 x i j ∈ { x 1 , ⋯ , x n } x_{i_j}\in \{x_1,\cdots,x_n\} x i j ∈ { x 1 , ⋯ , x n } m m m
d : \mathrm d: d : k − k- k − → \rightarrow → k + 1 − k+1- k + 1 −
d ( ∑ i f i ( x 1 , x 2 ⋯ , x n ) d x i 1 d x i 2 ⋯ d x i m ) = ∑ i d ( f i ( x 1 , x 2 ⋯ , x n ) d x i 1 d x i 2 ⋯ d x i m ) = ∑ i ∑ j ∂ f i ∂ x j d x j d x i 1 d x i 2 ⋯ d x i m \mathrm d \left(\sum_i f_i(x_1,x_2\cdots,x_n) \mathrm d x_{i_1} \mathrm d x_{i_2}\cdots\mathrm d x_{i_m}\right)\\
=\sum_i \mathrm d \left(f_i(x_1,x_2\cdots,x_n) \mathrm d x_{i_1} \mathrm d x_{i_2}\cdots\mathrm d x_{i_m}\right)\\
=\sum_{i}\sum_j \frac{\partial f_i}{\partial x_j} \mathrm d x_j \mathrm d x_{i_1} \mathrm d x_{i_2}\cdots\mathrm d x_{i_m}
d ( i ∑ f i ( x 1 , x 2 ⋯ , x n ) d x i 1 d x i 2 ⋯ d x i m ) = i ∑ d ( f i ( x 1 , x 2 ⋯ , x n ) d x i 1 d x i 2 ⋯ d x i m ) = i ∑ j ∑ ∂ x j ∂ f i d x j d x i 1 d x i 2 ⋯ d x i m
引入规则:
交换相邻两项:d x i 1 ⋯ d x i l d x i l + 1 ⋯ d x i k = d x i 1 ⋯ d x i l + 1 d x i l ⋯ d x i k \mathrm d x_{i_1}\cdots \mathrm d x_{i_l} \mathrm d x_{i_{l+1}}\cdots \mathrm d x_{i_k}=\mathrm d x_{i_1}\cdots \mathrm d x_{i_{l+1}} \mathrm d x_{i_{l}}\cdots \mathrm d x_{i_k} d x i 1 ⋯ d x i l d x i l + 1 ⋯ d x i k = d x i 1 ⋯ d x i l + 1 d x i l ⋯ d x i k
存在相同的项:∃ k , l : i k = i l \exists k,l:i_k=i_l ∃ k , l : i k = i l
∂ ( x , y ) ∂ ( u , v ) ⋅ d u d v = d x d y \displaystyle \frac{\partial (x,y)}{\partial (u,v)}\cdot \mathrm{d} u \mathrm{d} v=\mathrm{d} x\mathrm{d} y ∂ ( u , v ) ∂ ( x , y ) ⋅ d u d v = d x d y
统一公式
∫ C ω = ∬ int C d ω \boxed{\int_C \omega =\iint_{\operatorname{int} C}\mathrm d \omega}
∫ C ω = ∬ i n t C d ω
ω : \omega: ω : k − k- k − C : k C:k C : k int C \operatorname{int}C i n t C k − 1 k-1 k − 1
例如 Gauss 公式 :
∯ ∂ V P d y d z + Q d z d x + R d x d y = ∭ V ∂ P ∂ x d x d y d z + ∂ P ∂ y d y d y d z ⏟ = 0 + ∂ Q ∂ y d y d z d x ⏟ = d x d y d z + ∂ R ∂ z d z d x d y = ∭ Ω ( ∂ P ∂ x + ∂ Q ∂ y + ∂ R ∂ z ) d V \oiint_{\partial V} P\mathrm d y\mathrm d z+Q\mathrm d z\mathrm d x+R\mathrm d x\mathrm d y\\=\iiint_V \frac{\partial P}{\partial x}\mathrm d x\mathrm d y\mathrm d z+\underbrace{\frac{\partial P}{\partial y}\mathrm d y\mathrm d y\mathrm d z}_{=0}+\frac{\partial Q}{\partial y}\underbrace{\mathrm d y\mathrm d z\mathrm d x}_{=\mathrm d x\mathrm d y\mathrm d z}+\frac{\partial R}{\partial z} \mathrm d z\mathrm d x\mathrm d y\\
=\iiint_{\Omega}\left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}\right)\mathrm d V
∬ ∂ V P d y d z + Q d z d x + R d x d y = ∭ V ∂ x ∂ P d x d y d z + = 0 ∂ y ∂ P d y d y d z + ∂ y ∂ Q = d x d y d z d y d z d x + ∂ z ∂ R d z d x d y = ∭ Ω ( ∂ x ∂ P + ∂ y ∂ Q + ∂ z ∂ R ) d V
第二类曲面积分的换元
∯ ∂ V P d y d z + Q d z d x + R d x d y = ∯ ∂ V P ∂ ( y , z ) ∂ ( u , v ) d u d v ⋯ \oiint_{\partial V} P\mathrm{d} y\mathrm{d} z+Q\mathrm{d} z\mathrm{d} x+R\mathrm{d} x \mathrm{d} y\\
=\oiint_{\partial V}P \frac{\partial (y,z)}{\partial (u,v)} \mathrm{d} u\mathrm{d}v \cdots
∬ ∂ V P d y d z + Q d z d x + R d x d y = ∬ ∂ V P ∂ ( u , v ) ∂ ( y , z ) d u d v ⋯
∯ ∂ V P d y d z + Q d z d x + R d x d y = ∯ ∂ V P d y d x ⋅ z x + Q z y ⋅ d y d x + R d x d y = ( ± ) ∬ D x y ( − P z x − Q z y + R ) d x d y = ( ± ) ∬ D x y ( F x F z ⋅ P + F y F z ⋅ Q + R ) d x d y \oiint_{\partial V} P\mathrm{d} y\mathrm{d} z+Q\mathrm{d} z\mathrm{d} x+R\mathrm{d} x \mathrm{d} y\\
=\oiint_{\partial V} P \mathrm{d} y \mathrm{d} x \cdot z_x+Qz_y \cdot \mathrm{d} y \mathrm{d} x+R\mathrm{d} x\mathrm{d} y\\
=(\pm)\iint_{D_{xy}}(-Pz_x-Qz_y+R)\mathrm d x\mathrm d y\\=(\pm)\iint_{D_{xy}} \left(\frac{F_x}{F_z}\cdot P+\frac{F_y}{F_z} \cdot Q+R\right)\mathrm d x\mathrm d y
∬ ∂ V P d y d z + Q d z d x + R d x d y = ∬ ∂ V P d y d x ⋅ z x + Q z y ⋅ d y d x + R d x d y = ( ± ) ∬ D x y ( − P z x − Q z y + R ) d x d y = ( ± ) ∬ D x y ( F z F x ⋅ P + F z F y ⋅ Q + R ) d x d y
*Stokes 公式 :
∫ C P d x + Q d y + R d z = ∫ C ( ∂ P ∂ y d y d x + ∂ P ∂ z d z d x ) ⋯ = ∬ Σ ( ∂ R ∂ y − ∂ Q ∂ z ) d y d z + ( ∂ P ∂ z − ∂ R ∂ x ) d z d x + ( ∂ Q ∂ x − ∂ P ∂ y ) d x d y \int_C P\mathrm d x+Q\mathrm d y+R\mathrm d z=\int_C \left(\frac{\partial P}{\partial y}\mathrm d y\mathrm d x+\frac{\partial P}{\partial z} \mathrm d z\mathrm d x\right)\cdots\\=\iint_{\Sigma} \left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right) \mathrm{d} y \mathrm{d} z+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right) \mathrm{d} z \mathrm{d} x+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \mathrm{d} x \mathrm{d} y
∫ C P d x + Q d y + R d z = ∫ C ( ∂ y ∂ P d y d x + ∂ z ∂ P d z d x ) ⋯ = ∬ Σ ( ∂ y ∂ R − ∂ z ∂ Q ) d y d z + ( ∂ z ∂ P − ∂ x ∂ R ) d z d x + ( ∂ x ∂ Q − ∂ y ∂ P ) d x d y
Green 公式 是 Stokes 公式的特殊情况。
已知 C C C { ( x − 6 ) 2 + y 2 = 6 z = 24 − x 2 − y 2 \left\{\begin{aligned}(x-\sqrt{6})^2+y^2=6\\z=\sqrt{24-x^2-y^2}\end{aligned}\right. { ( x − 6 ) 2 + y 2 = 6 z = 2 4 − x 2 − y 2 ( 2 6 , 0 , 0 ) (2\sqrt{6},0,0) ( 2 6 , 0 , 0 ) ( 0 , 0 , 2 6 ) (0,0,2\sqrt{6}) ( 0 , 0 , 2 6 )
∫ C 5 y d x + d z \int_C 5y \mathrm d x+\mathrm d z
∫ C 5 y d x + d z
分为两部分计算,第二部分 ∫ C d z \int_C \mathrm d z ∫ C d z 2 6 2\sqrt{6} 2 6
第一部分可以参数方程换元。代入 x = 6 cos θ + 6 , y = 6 sin θ x=\sqrt{6}\cos \theta+\sqrt{6},y=\sqrt{6}\sin\theta x = 6 cos θ + 6 , y = 6 sin θ
∫ 0 π 5 6 sin θ ( − 6 sin θ ) d θ = − 30 ∫ 0 π sin 2 θ d θ = − 60 ∫ 0 π / 2 sin 2 θ d θ = − 60 π 2 1 2 = − 15 π \int_0^\pi 5\sqrt{6}\sin\theta(-\sqrt{6}\sin\theta)\mathrm d \theta=-30\int_0^\pi \sin^2\theta\mathrm d \theta=-60\int_0^{\pi/2} \sin^2\theta\mathrm d \theta=-60\frac{\pi}{2}\frac{1}{2}=-15\pi
∫ 0 π 5 6 sin θ ( − 6 sin θ ) d θ = − 3 0 ∫ 0 π sin 2 θ d θ = − 6 0 ∫ 0 π / 2 sin 2 θ d θ = − 6 0 2 π 2 1 = − 1 5 π
另外一种换元方法,x 2 + y 2 = a x x^2+y^2=ax x 2 + y 2 = a x
{ x = a cos 2 θ y = a cos θ sin θ \left\{\begin{aligned}&x=a\cos ^2\theta \\&y=a\cos \theta \sin\theta\end{aligned}\right.
{ x = a cos 2 θ y = a cos θ sin θ
这样可以避免常数项。
计算 ∮ C z d s \displaystyle \oint_C z\mathrm d s ∮ C z d s C C C x 2 + y 2 + z 2 = 2 x x^2+y^2+z^2=2x x 2 + y 2 + z 2 = 2 x z = x 2 + y 2 z=\sqrt{x^2+y^2} z = x 2 + y 2 z ≥ 0 z\ge 0 z ≥ 0
如何求出来一个参数方程,先得到关于 x , y x,y x , y z z z
x 2 + y 2 = x x^2+y^2=x
x 2 + y 2 = x
如果使用第一种换元方法,会比较烦。
使用第二种换元方法,x = cos 2 θ , y = cos θ sin θ , z = cos θ x=\cos ^2\theta,y=\cos \theta\sin\theta,z=\cos \theta x = cos 2 θ , y = cos θ sin θ , z = cos θ z ≥ 0 z\ge 0 z ≥ 0 − π 2 ≤ θ ≤ π 2 \displaystyle -\frac{\pi}{2} \le \theta \le \frac{\pi}{2} − 2 π ≤ θ ≤ 2 π
d s = x ′ ( θ ) + y ′ ( θ ) + z ′ ( θ ) d θ = 1 + sin 2 θ d θ \mathrm d s=\sqrt{x'(\theta)+y'(\theta)+z'(\theta)}\mathrm d \theta=\sqrt{1+\sin^2\theta}\mathrm d \theta
d s = x ′ ( θ ) + y ′ ( θ ) + z ′ ( θ ) d θ = 1 + sin 2 θ d θ
转化为
I = ∫ − π 2 π 2 cos θ 1 + sin 2 θ d θ = ∫ − 1 1 1 + t 2 d t I=\int_{-\frac{\pi}{2}}^\frac{\pi}{2} \cos\theta\sqrt{1+\sin^2\theta}\mathrm d \theta=\int_{-1}^1 \sqrt{1+t^2}\mathrm d t
I = ∫ − 2 π 2 π cos θ 1 + sin 2 θ d θ = ∫ − 1 1 1 + t 2 d t
这个积分怎么积,分部积分:
∫ 1 + t 2 d t = t 1 + t 2 − ∫ t ⋅ t 1 + t 2 d t = t 1 + t 2 − ∫ 1 + t 2 d t − ∫ 1 1 + t 2 d t = \int \sqrt{1+t^2}\mathrm d t=t\sqrt{1+t^2}-\int t \cdot \frac{t}{\sqrt{1+t^2}}\mathrm d t=t\sqrt{1+t^2}-\int\sqrt{1+t^2}\mathrm d t-\int\frac{1}{\sqrt{1+t^2}}\mathrm d t=
∫ 1 + t 2 d t = t 1 + t 2 − ∫ t ⋅ 1 + t 2 t d t = t 1 + t 2 − ∫ 1 + t 2 d t − ∫ 1 + t 2 1 d t =
得到
∫ 1 + t 2 = 1 2 ( t 1 + t 2 + ln ( t + 1 + t 2 ) ) + C \int \sqrt{1+t^2}=\frac{1}{2}(t\sqrt{1+t^2}+\ln(t+\sqrt{1+t^2}))+C
∫ 1 + t 2 = 2 1 ( t 1 + t 2 + ln ( t + 1 + t 2 ) ) + C
因此结果是 2 + ln ( 1 + 2 ) \sqrt{2}+\ln(1+\sqrt{2}) 2 + ln ( 1 + 2 )
计算 $\displaystyle \oint_L (x2+y 2-z^2)\mathrm d x+(y2+z 2-x^2)\mathrm d y+(z2+x 2-y^2)\mathrm d z $,其中 L L L x 2 + y 2 + z 2 = 6 y x^2+y^2+z^2=6y x 2 + y 2 + z 2 = 6 y x 2 + y 2 = 4 y ( z ≥ 0 ) x^2+y^2=4y(z\ge0) x 2 + y 2 = 4 y ( z ≥ 0 ) z z z
z 2 = 2 y ⇒ z = 2 y z^2=2y\Rightarrow z=\sqrt{2y} z 2 = 2 y ⇒ z = 2 y z ≥ 0 z\ge0 z ≥ 0
换元:x = 4 sin θ cos θ , y = 4 sin 2 θ , z = 2 2 sin θ x=4\sin\theta \cos\theta,y=4\sin^2\theta,z=2\sqrt{2}\sin\theta x = 4 sin θ cos θ , y = 4 sin 2 θ , z = 2 2 sin θ θ \theta θ 0 ≤ θ ≤ π 0\le \theta \le \pi 0 ≤ θ ≤ π
接下来只用处理三角函数高次幂的积分,用 Wallis 公式。
答案是 − 8 π -8\pi − 8 π
计算 ∮ C x 2 d s \displaystyle \oint_C x^2 \mathrm d s ∮ C x 2 d s C : x 2 + y 2 + z 2 = a 2 C:x^2+y^2+z^2=a^2 C : x 2 + y 2 + z 2 = a 2 x + y + z = 0 x+y+z=0 x + y + z = 0
I = 1 3 ∮ C ( x 2 + y 2 + z 2 ) d s = 1 3 a 2 × 2 π a = 2 3 π a 3 I=\frac{1}{3}\oint_C (x^2+y^2+z^2) \mathrm d s=\frac{1}{3}a^2 \times 2\pi a=\frac{2}{3}\pi a^3
I = 3 1 ∮ C ( x 2 + y 2 + z 2 ) d s = 3 1 a 2 × 2 π a = 3 2 π a 3
计算 ∮ C x y d s \displaystyle \oint_C xy \mathrm d s ∮ C x y d s C : x 2 + y 2 + z 2 = a 2 C:x^2+y^2+z^2=a^2 C : x 2 + y 2 + z 2 = a 2 x + y + z = 0 x+y+z=0 x + y + z = 0
轮换对称性:
I = 1 3 ∮ C ( x y + y z + z x ) d s = 1 3 ∮ C ( x + y + z ) 2 − ( x 2 + y 2 + z 2 ) 2 d s = − a 2 6 ∮ C d s = − a 2 6 2 π a = − π 3 a 3 I=\frac{1}{3}\oint_C (xy+yz+zx)\mathrm d s=\frac{1}{3}\oint_C\frac{(x+y+z)^2-(x^2+y^2+z^2)}{2}\mathrm d s\\
=-\frac{a^2}{6}\oint_C \mathrm d s=-\frac{a^2}{6}2\pi a=-\frac{\pi}{3}a^3
I = 3 1 ∮ C ( x y + y z + z x ) d s = 3 1 ∮ C 2 ( x + y + z ) 2 − ( x 2 + y 2 + z 2 ) d s = − 6 a 2 ∮ C d s = − 6 a 2 2 π a = − 3 π a 3
计算 ∮ C x 2 d s \displaystyle \oint_C x^2 \mathrm d s ∮ C x 2 d s C : x 2 + y 2 + z 2 = a 2 C:x^2+y^2+z^2=a^2 C : x 2 + y 2 + z 2 = a 2 x + y + z = c ( c 2 < 3 a 2 ) x+y+z=c(c^2 <3a^2) x + y + z = c ( c 2 < 3 a 2 )
只需要知道圆周的半径:
d = c 1 + 1 + 1 = c 3 , r = a 2 − c 2 3 d=\frac{c}{\sqrt{1+1+1}}=\frac{c}{\sqrt{3}},r=\sqrt{a^2-\frac{c^2}{3}}
d = 1 + 1 + 1 c = 3 c , r = a 2 − 3 c 2
答案是
2 3 π a 2 a 2 − c 2 3 \frac{2}{3}\pi a^2\sqrt{a^2-\frac{c^2}{3}}
3 2 π a 2 a 2 − 3 c 2
设 f ( x ) f(x) f ( x ) a , b ∈ R a,b \in\R a , b ∈ R ∮ C a f ( x ) + b f ( y ) f ( x ) + f ( y ) d s \displaystyle \oint_C \frac{af(x)+bf(y)}{f(x)+f(y)}\mathrm d s ∮ C f ( x ) + f ( y ) a f ( x ) + b f ( y ) d s C C C D = { ( x , y ) ∣ ∣ x ∣ + ∣ y ∣ ≤ 1 } D=\{(x,y) \mid |x|+|y| \le 1\} D = { ( x , y ) ∣ ∣ x ∣ + ∣ y ∣ ≤ 1 }
边界满足轮换对称性的条件。
2 I = ∮ C ( a + b ) ( f ( x ) + f ( y ) ) f ( x ) + f ( y ) d s = ( a + b ) l = 4 2 ( a + b ) 2I=\oint_C \frac{(a+b)(f(x)+f(y))}{f(x)+f(y)}\mathrm d s=(a+b)l=4\sqrt{2}(a+b)
2 I = ∮ C f ( x ) + f ( y ) ( a + b ) ( f ( x ) + f ( y ) ) d s = ( a + b ) l = 4 2 ( a + b )
I = 2 2 ( a + b ) I=2\sqrt{2}(a+b)
I = 2 2 ( a + b )
设 L L L D : x 2 ≤ y ≤ 2 x , 1 ≤ x y ≤ 2 \displaystyle D:\frac{x}{2}\le y\le 2x,1 \le xy \le 2 D : 2 x ≤ y ≤ 2 x , 1 ≤ x y ≤ 2 ∮ L e x 2 y 2 ( ( y − 1 x ) d x + ( x + 1 y ) d y ) \displaystyle \oint_L e^{x^2y^2}((y-\frac{1}{x})\mathrm d x+(x+\frac{1}{y})\mathrm d y) ∮ L e x 2 y 2 ( ( y − x 1 ) d x + ( x + y 1 ) d y )
不能直接代换,因为没有对应的公式,使用格林公式:
I = ∬ D ( Q x − P y ) d x d y = 4 ∬ D e x 2 y 2 x y d x d y I=\iint_D (Q_x-P_y)\mathrm d x\mathrm d y=4\iint_D e^{x^2y^2} xy \mathrm d x\mathrm d y
I = ∬ D ( Q x − P y ) d x d y = 4 ∬ D e x 2 y 2 x y d x d y
然后再令 u = x y , v = y / x u=xy,v=y/x u = x y , v = y / x ∣ J ∣ = 1 / 2 v |J|=1/2v ∣ J ∣ = 1 / 2 v
∫ 0 1 e u 2 d ( u 2 ) ∫ 1 / 2 2 d v v = ( e 4 − e ) 2 ln 2 \int_0^1 e^{u^2} \mathrm d (u^2) \int_{1/2}^2 \frac{\mathrm d v}{v}=(e^4-e)2\ln 2
∫ 0 1 e u 2 d ( u 2 ) ∫ 1 / 2 2 v d v = ( e 4 − e ) 2 ln 2
计算 I = ∬ Σ x y z x 2 + y 2 + z 2 d x d y \displaystyle I=\iint_\Sigma \frac{xyz}{x^2+y^2+z^2}\mathrm d x\mathrm d y I = ∬ Σ x 2 + y 2 + z 2 x y z d x d y Σ : x 2 + y 2 + z 2 = 1 ( x , y ≥ 0 ) \Sigma:x^2+y^2+z^2 =1 (x,y \ge 0) Σ : x 2 + y 2 + z 2 = 1 ( x , y ≥ 0 )
这个一眼内部是有奇点的,高斯公式不好做。
I = ∬ Σ x y z d x d y = 2 ∬ Σ , z ≥ 0 x y 1 − x 2 − y 2 d x d y = 2 ∬ D x y x y 1 − x 2 − y 2 d σ I=\iint_\Sigma xyz \mathrm d x\mathrm d y=2 \iint_{\Sigma ,z\ge 0} xy \sqrt{1-x^2-y^2} \mathrm d x\mathrm d y\\
=2\iint_{D_{xy}}xy \sqrt{1-x^2-y^2} \mathrm d \sigma
I = ∬ Σ x y z d x d y = 2 ∬ Σ , z ≥ 0 x y 1 − x 2 − y 2 d x d y = 2 ∬ D x y x y 1 − x 2 − y 2 d σ
极坐标换元,得到 2 π / 15 2\pi/15 2 π / 1 5
求 ∬ Σ − y d z d x + ( z + 1 ) d x d y \displaystyle \iint_\Sigma -y \mathrm d z\mathrm d x+(z+1)\mathrm d x\mathrm d y ∬ Σ − y d z d x + ( z + 1 ) d x d y Σ \Sigma Σ x 2 + y 2 = 4 x^2+y^2=4 x 2 + y 2 = 4 x + z = 2 x+z=2 x + z = 2 z = 0 z=0 z = 0
这个用高斯公式是比较好做的,因为 ∭ = 0 \iiint=0 ∭ = 0
上底面 x + z = 2 , x 2 + y 2 ≤ 4 x+z=2,x^2+y^2 \le 4 x + z = 2 , x 2 + y 2 ≤ 4
I 1 = ∬ Σ ( z + 1 ) d x d y = ∬ D x y ( 3 − x ) d x d y = 3 ∬ D x y d σ = 12 π I_1=\iint_\Sigma (z+1)\mathrm d x\mathrm d y=\iint_{D_{xy}} (3-x)\mathrm d x\mathrm d y=3\iint_{D_{xy}}\mathrm d \sigma=12\pi
I 1 = ∬ Σ ( z + 1 ) d x d y = ∬ D x y ( 3 − x ) d x d y = 3 ∬ D x y d σ = 1 2 π
下底面 x 2 + y 2 ≤ 4 , z = 0 x^2+y^2\le 4,z=0 x 2 + y 2 ≤ 4 , z = 0
I 2 = − ∬ Σ d x d y = − 4 π I_2=-\iint_\Sigma \mathrm d x\mathrm d y=-4\pi
I 2 = − ∬ Σ d x d y = − 4 π
I + I 1 + I 2 = 0 I+I_1+I_2=0 I + I 1 + I 2 = 0 I = − 8 π I=-8\pi I = − 8 π
求 ∬ Σ R x d y d z + ( z + R ) 2 d x d y x 2 + y 2 + z 2 ( R > 0 ) \displaystyle \iint_\Sigma \frac{Rx \mathrm d y\mathrm d z+(z+R)^2\mathrm d x\mathrm d y}{\sqrt{x^2+y^2+z^2}} (R>0) ∬ Σ x 2 + y 2 + z 2 R x d y d z + ( z + R ) 2 d x d y ( R > 0 ) Σ : z = − R 2 − x 2 − y 2 \Sigma:z=-\sqrt{R^2-x^2-y^2} Σ : z = − R 2 − x 2 − y 2
代入 x 2 + y 2 + z 2 = R \sqrt{x^2+y^2+z^2}=R x 2 + y 2 + z 2 = R
I = ∬ Σ x d y d z + ( R + 2 z + z 2 R ) d x d y I=\iint_{\Sigma} x\mathrm d y\mathrm d z+\left(R+2z+\frac{z^2}{R}\right)\mathrm d x\mathrm d y
I = ∬ Σ x d y d z + ( R + 2 z + R z 2 ) d x d y
高斯公式得到
I + ∬ Σ ′ x d y d z + ( R + 2 z + z 2 R ) d x d y = ∭ Ω ( 1 + 2 + 2 z R ) d V I+\iint_{\Sigma'} x\mathrm d y\mathrm d z+\left(R+2z+\frac{z^2}{R}\right)\mathrm d x\mathrm d y=\iiint_\Omega \left(1+2+\frac{2z}{R}\right)\mathrm d V
I + ∬ Σ ′ x d y d z + ( R + 2 z + R z 2 ) d x d y = ∭ Ω ( 1 + 2 + R 2 z ) d V
对于后面一个三重积分,第一部分是体积的三倍,也就是 2 π R 3 2\pi R^3 2 π R 3
2 R ∭ Ω z d V = 2 R ∫ − R 0 z d z ∬ D x y d σ = π R ∫ − R 0 ( R 2 − z 2 ) d z 2 = π R ∫ R 2 0 ( R 2 − u ) d u = − 1 2 π R 3 \frac{2}{R} \iiint_\Omega z \mathrm d V=\frac{2}{R} \int_{-R}^0 z \mathrm d z \iint_{D_{xy}}\mathrm d \sigma=\frac{\pi}{R} \int_{-R}^0 (R^2-z^2) \mathrm d z^2=\frac{\pi}{R} \int_{R^2}^0 (R^2-u)\mathrm d u=-\frac{1}{2} \pi R^3
R 2 ∭ Ω z d V = R 2 ∫ − R 0 z d z ∬ D x y d σ = R π ∫ − R 0 ( R 2 − z 2 ) d z 2 = R π ∫ R 2 0 ( R 2 − u ) d u = − 2 1 π R 3
因此三重积分的结果是 3 π R 3 / 2 3\pi R^3/2 3 π R 3 / 2
∬ D R d σ = π R 3 \iint_{D} R \mathrm d \sigma=\pi R^3
∬ D R d σ = π R 3
⇒ I = π 2 R 3 \Rightarrow I=\frac{\pi}{2}R^3
⇒ I = 2 π R 3
求 ∇ ⋅ ( ∇ r ) \nabla\cdot (\nabla r) ∇ ⋅ ( ∇ r ) r = x 2 + y 2 + z 2 r=\sqrt{x^2+y^2+z^2} r = x 2 + y 2 + z 2
∇ r \nabla r ∇ r ∇ ⋅ u \nabla \cdot u ∇ ⋅ u
∇ r = ( x r , y r , z r ) \displaystyle \nabla r=\left(\frac{x}{r},\frac{y}{r},\frac{z}{r}\right) ∇ r = ( r x , r y , r z )
∇ ⋅ ( ∇ r ) = r 2 − x 2 r 3 + r 2 − y 2 r 3 + r 2 − z 2 r 3 = 2 r \displaystyle \nabla\cdot (\nabla r)=\frac{r^2-x^2}{r^3}+\frac{r^2-y^2}{r^3}+\frac{r^2-z^2}{r^3}=\frac{2}{r} ∇ ⋅ ( ∇ r ) = r 3 r 2 − x 2 + r 3 r 2 − y 2 + r 3 r 2 − z 2 = r 2
设 f ( x , y , z ) f(x,y,z) f ( x , y , z ) ∇ × ( ∇ f ) = 0 \nabla \times (\nabla f)=0 ∇ × ( ∇ f ) = 0
∣ i ⃗ j ⃗ k ⃗ ∂ ∂ x ∂ ∂ y ∂ ∂ z ∂ f ∂ x ∂ f ∂ y ∂ f ∂ z ∣ = 0 \left|\begin{array}{lll}
\vec{i} & \vec{j} & \vec{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
\frac{\partial f}{\partial x} & \frac{\partial f}{\partial y} & \frac{\partial f}{\partial z}
\end{array}\right|=0
∣ ∣ ∣ ∣ ∣ ∣ ∣ i ∂ x ∂ ∂ x ∂ f j ∂ y ∂ ∂ y ∂ f k ∂ z ∂ ∂ z ∂ f ∣ ∣ ∣ ∣ ∣ ∣ ∣ = 0
物理意义:梯度场无旋,是保守场,有势。
解: y ′ − 1 x y = − e x y 2 y^{\prime}-\frac{1}{x} y=-e^x y^2 y ′ − x 1 y = − e x y 2 y ′ + f ( x ) y = g ( x ) y α y^{\prime}+f(x) y=g(x) y^\alpha y ′ + f ( x ) y = g ( x ) y α
ı ^ z = y 1 − α 则 z ′ = ( 1 − α ) y − α y ′ ⇒ 1 1 − α z ′ + f ( x ) ⋅ z = g ( x ) z = 1 y ⇒ − z ′ + ( − 1 x ) ⋅ z = − e x z ′ + 1 x z = e x \begin{aligned}
& \hat{\imath} z=y^{1-\alpha} \quad \text { 则 } z^{\prime}=(1-\alpha) y^{-\alpha} y^{\prime} \\
& \Rightarrow \frac{1}{1-\alpha} z^{\prime}+f(x) \cdot z=g(x) \\
& z=\frac{1}{y} \quad\Rightarrow-z^{\prime}+\left(-\frac{1}{x}\right) \cdot z=-e^x \\
& z^{\prime}+\frac{1}{x} z=e^x \\
&
\end{aligned}
ı ^ z = y 1 − α 则 z ′ = ( 1 − α ) y − α y ′ ⇒ 1 − α 1 z ′ + f ( x ) ⋅ z = g ( x ) z = y 1 ⇒ − z ′ + ( − x 1 ) ⋅ z = − e x z ′ + x 1 z = e x
用常数变异法 z ′ + 1 x z = 0 z^{\prime}+\frac{1}{x} z=0 z ′ + x 1 z = 0
⇒ z = c x ⇒ z = c ( x ) x c ′ ( x ) ⋅ x − c ( x ) x 2 + c ( x ) x 2 = e x ⇒ c ′ ( x ) = x e x ⇒ c ( x ) = ( x − 1 ) e x + c c = 2 z = ( x − 1 ) e x + 2 x y = x ( x − 1 ) e x + 2 \begin{aligned}
& \Rightarrow z=\frac{c}{x} \Rightarrow z=\frac{c(x)}{x} \\
& \frac{c^{\prime}(x) \cdot x-c(x)}{x^2}+\frac{c(x)}{x^2}=e^x \Rightarrow c^{\prime}(x)=x e^x \\
& \Rightarrow c(x)=(x-1) e^x+c \quad c=2 \\
& z=\frac{(x-1) e^x+2}{x} \quad y=\frac{x}{(x-1) e^x+2}
\end{aligned}
⇒ z = x c ⇒ z = x c ( x ) x 2 c ′ ( x ) ⋅ x − c ( x ) + x 2 c ( x ) = e x ⇒ c ′ ( x ) = x e x ⇒ c ( x ) = ( x − 1 ) e x + c c = 2 z = x ( x − 1 ) e x + 2 y = ( x − 1 ) e x + 2 x
已知 x o y xoy x o y D : x > 1 D:x>1 D : x > 1
F = ( y ( x − 1 ) 2 + y 2 , a ( x − 1 ) ( x − 1 ) 2 + y 2 ) \boldsymbol F =\left(\frac{y}{(x-1)^2+y^2},\frac{a(x-1)}{(x-1)^2+y^2}\right)
F = ( ( x − 1 ) 2 + y 2 y , ( x − 1 ) 2 + y 2 a ( x − 1 ) )
是梯度,曲线 C C C ( 2 , 0 ) (2,0) ( 2 , 0 ) ( 3 , 2 ) (3,2) ( 3 , 2 ) ∫ C u x d x + u y d y = u ( 3 , 2 ) − u ( 2 , 0 ) \displaystyle\int _C u_x \mathrm{d} x+u_y \mathrm{d} y=u(3,2)-u(2,0) ∫ C u x d x + u y d y = u ( 3 , 2 ) − u ( 2 , 0 )
u ( x , y ) = ∫ y ( x − 1 ) 2 + y 2 d x = arctan x − 1 y + C u(x,y)=\int \frac{y}{(x-1)^2+y^2} \mathrm{d} x=\arctan \frac{x-1}{y}+C
u ( x , y ) = ∫ ( x − 1 ) 2 + y 2 y d x = arctan y x − 1 + C
关键是 u ( 2 , 0 ) u(2,0) u ( 2 , 0 ) 0 + 0^+ 0 +
( π 4 + C ) − ( π 2 + C ) = π 4 \left(\frac{\pi}{4}+C\right)-\left(\frac{\pi}{2}+C\right)=\frac{\pi}{4}
( 4 π + C ) − ( 2 π + C ) = 4 π
两条路径围成的区域中间没有奇点,才和路径无关。
计算 ∫ C x − y x 2 + y 2 d x + x + y x 2 + y 2 d y \displaystyle\int_C \frac{x-y}{x^2+y^2}\mathrm d x+\frac{x+y}{x^2+y^2} \mathrm{d} y ∫ C x 2 + y 2 x − y d x + x 2 + y 2 x + y d y C C C A ( − a , 0 ) A(-a,0) A ( − a , 0 ) x 2 a 2 + y 2 b 2 = 1 ( y ≥ 0 ) \displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(y\ge 0) a 2 x 2 + b 2 y 2 = 1 ( y ≥ 0 ) B ( a , 0 ) B(a,0) B ( a , 0 )
观察到 Q x = P y Q_x=P_y Q x = P y
取半径为 a a a x = a cos θ , y = a sin θ , θ : π → 0 x=a\cos \theta,y=a\sin\theta,\theta :\pi \to 0 x = a cos θ , y = a sin θ , θ : π → 0
∫ π 0 sin 2 θ + cos 2 θ d θ = − π \int_\pi^0 \sin^2\theta+\cos^2\theta \mathrm{d} \theta=-\pi
∫ π 0 sin 2 θ + cos 2 θ d θ = − π
也可以观察到原函数是:
u ( x , y ) = 1 2 ln ( x 2 + y 2 ) − arctan x y + C u(x,y)=\frac{1}{2}\ln(x^2+y^2)-\arctan \frac{x}{y}+C
u ( x , y ) = 2 1 ln ( x 2 + y 2 ) − arctan y x + C
I = u ( a , 0 ) − u ( − a , 0 ) = − arctan a 0 + + arctan − a 0 + = − π I=u(a,0)-u(-a,0)=-\arctan \frac{a}{0^+}+\arctan \frac{-a}{0^+}=-\pi
I = u ( a , 0 ) − u ( − a , 0 ) = − arctan 0 + a + arctan 0 + − a = − π
计算 ∮ C ( x + 4 y ) d y + ( x − y ) d x x 2 + 4 y 2 \displaystyle \oint_C \frac{(x+4y)\mathrm d y+(x-y)\mathrm d x}{x^2+4y^2} ∮ C x 2 + 4 y 2 ( x + 4 y ) d y + ( x − y ) d x C C C
首先观察到积分与路径无关。
换元 x = ε cos θ , y = ε 2 sin θ x=\varepsilon\cos \theta,y=\frac{\varepsilon}{2} \sin\theta x = ε cos θ , y = 2 ε sin θ
正向曲线图形在左手边,结果应该是 π \pi π
已知 S S S { x 2 + 3 y 2 = 1 z = 0 \left\{
\begin{aligned}
&x^2+3y^2=1\\
&z=0\\
\end{aligned}
\right. { x 2 + 3 y 2 = 1 z = 0 y y y Σ \Sigma Σ P ( x , y , z ) P(x,y,z) P ( x , y , z ) ρ ( x , y , z ) \rho(x,y,z) ρ ( x , y , z ) λ , μ , ν \lambda,\mu,\nu λ , μ , ν S S S
原题化为 z = 1 − x 2 − 3 y 2 z=\sqrt{1-x^2-3y^2} z = 1 − x 2 − 3 y 2 z x , z y z_x,z_y z x , z y
n = ( − z x , − z y , 1 ) \boldsymbol n=(-z_x,-z_y,1) n = ( − z x , − z y , 1 )
n 0 = n / ∣ ∣ n ∣ ∣ \boldsymbol n^0=\boldsymbol n/||\boldsymbol n|| n 0 = n / ∣ ∣ n ∣ ∣ λ , μ , ν \lambda,\mu,\nu λ , μ , ν
(1) ∬ S z ρ ( x , y , z ) d S \displaystyle \iint_S \frac{z}{\rho(x,y,z)} \mathrm{d} S ∬ S ρ ( x , y , z ) z d S
(2) ∬ S z ( λ x + 3 μ y + ν z ) d S \displaystyle \iint_S z(\lambda x+3\mu y+\nu z) \mathrm d S ∬ S z ( λ x + 3 μ y + ν z ) d S
方法1
( λ , μ , ν ) ⋅ ( z x , 3 z y , z 2 ) d S = ( z x , 3 z y , z 2 ) ⋅ d S (\lambda,\mu,\nu)\cdot (zx,3zy,z^2)\mathrm d S=(zx,3zy,z^2)\cdot \mathrm d \boldsymbol S ( λ , μ , ν ) ⋅ ( z x , 3 z y , z 2 ) d S = ( z x , 3 z y , z 2 ) ⋅ d S
∭ Ω 6 z d V = ∫ 0 1 6 z ( 1 − z 2 ) ⋅ 1 3 π = 3 2 π \iiint_\Omega 6z \mathrm d V=\int_0^1 6z (1-z^2) \cdot \frac{1}{\sqrt{3}}\pi=\frac{\sqrt{3}}{2}\pi
∭ Ω 6 z d V = ∫ 0 1 6 z ( 1 − z 2 ) ⋅ 3 1 π = 2 3 π
方法2
计算出 λ , μ , ν \lambda,\mu,\nu λ , μ , ν
很简单,不写了
设 C C C l \boldsymbol l l n \boldsymbol n n C C C ∮ C cos < l , n > d s = 0 \displaystyle \oint_C \cos <\boldsymbol l,\boldsymbol n> \mathrm{d} s=0 ∮ C cos < l , n > d s = 0
cos < l , n > d s = l x 0 cos β − l y 0 cos α d s = l x 0 d x + l y 0 d y \cos <\boldsymbol l,\boldsymbol n>\mathrm d s=l_x^0 \cos\beta-l_y^0 \cos \alpha\mathrm d s=l_x^0\mathrm d x+l_y^0\mathrm d y cos < l , n > d s = l x 0 cos β − l y 0 cos α d s = l x 0 d x + l y 0 d y
物理意义:力场沿 l \boldsymbol l l
设 f ( x , y ) f(x,y) f ( x , y )
∬ D ( ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 ) d x d y = ∮ ∂ D + ∂ f ∂ n d S \iint_D \left(\frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2}\right)\mathrm d x\mathrm d y=\oint_{\partial D^+} \frac{\partial f}{\partial \boldsymbol n} \mathrm d S
∬ D ( ∂ x 2 ∂ 2 f + ∂ y 2 ∂ 2 f ) d x d y = ∮ ∂ D + ∂ n ∂ f d S
∂ f ∂ n = ∇ f ⋅ n 0 = ( f x , f y ) ( cos β , − cos α ) = f x d y − f y d x \displaystyle \frac{\partial f}{\partial \boldsymbol n}=\nabla f \cdot \boldsymbol n^0=(f_x,f_y)(\cos\beta,-\cos\alpha)=f_x \mathrm{d} y-f_y \mathrm{d} x ∂ n ∂ f = ∇ f ⋅ n 0 = ( f x , f y ) ( cos β , − cos α ) = f x d y − f y d x
方向余弦和外法向量的关系:τ : ( cos α , cos β ) ⇒ n : ( cos β , − cos α ) \boldsymbol \tau:(\cos\alpha,\cos\beta) \Rightarrow \boldsymbol n:(\cos\beta,-\cos\alpha) τ : ( cos α , cos β ) ⇒ n : ( cos β , − cos α )
利用格林公式就可以推出题目。
设 S S S
I = ∬ S ( x 3 − x ) d y d z + ( 2 y 3 − y ) d z d x + ( 3 z 3 − z ) d x d y I=\iint_{S} (x^3-x)\mathrm d y\mathrm d z+(2y^3-y)\mathrm{d} z\mathrm{d} x+(3z^3-z)\mathrm{d} x\mathrm{d} y
I = ∬ S ( x 3 − x ) d y d z + ( 2 y 3 − y ) d z d x + ( 3 z 3 − z ) d x d y
试证明,曲面积分 I I I − 4 6 15 π \displaystyle -\frac{4\sqrt{6}}{15}\pi − 1 5 4 6 π
利用高斯公式,转化为:
3 ∭ V ( x 2 + 2 y 2 + 3 z 2 − 1 ) d x d y d z ≥ − 4 6 15 π 3\iiint_V (x^2+2y^2+3z^2-1)\mathrm d x \mathrm d y\mathrm d z\ge -\frac{4\sqrt{6}}{15}\pi
3 ∭ V ( x 2 + 2 y 2 + 3 z 2 − 1 ) d x d y d z ≥ − 1 5 4 6 π
令 u = x , v = 2 y , w = 3 z u=x,v=\sqrt{2} y,w=\sqrt{3} z u = x , v = 2 y , w = 3 z
∭ V ( u 2 + v 2 + w 2 − 1 ) ≥ − 8 15 π \iiint_V (u^2+v^2+w^2-1)\ge -\frac{8}{15}\pi
∭ V ( u 2 + v 2 + w 2 − 1 ) ≥ − 1 5 8 π
由于这个表示方法有轮换对称性,有理由相信最小值对应的区域也是对称的,应该是一个球 u 2 + v 2 + w 2 ≤ a 2 u^2+v^2+w^2 \le a^2 u 2 + v 2 + w 2 ≤ a 2
三重积分的结果是:
4 π ( 1 5 a 5 − 1 3 a 3 ) 4\pi \left(\frac{1}{5}a^5-\frac{1}{3}a^3\right)
4 π ( 5 1 a 5 − 3 1 a 3 )
令导数为 0 0 0 a = 1 a=1 a = 1 a = 0 a=0 a = 0 − 8 π / 15 -8\pi/15 − 8 π / 1 5

法一 先计算一个 1 / 4 1/4 1 / 4
x ˉ = ∫ 0 π 2 a cos θ d s ∫ 0 π 2 d s \bar{x}=\frac{\int_0^\frac{\pi}{2}a\cos\theta\mathrm d s}{\int_0^\frac{\pi}{2} \mathrm d s}
x ˉ = ∫ 0 2 π d s ∫ 0 2 π a cos θ d s
然后 d s = a cos 2 θ + sin 2 θ d θ = a d θ \mathrm d s=a\sqrt{\cos^2\theta+\sin^2\theta}\mathrm d \theta=a\mathrm d \theta d s = a cos 2 θ + sin 2 θ d θ = a d θ
得到
x ˉ = a 2 π 2 a = 2 π a \bar x=\frac{a^2}{\frac{\pi}{2} a}=\frac{2}{\pi}a
x ˉ = 2 π a a 2 = π 2 a
然后三段圆弧里面两段对 x x x 2 / 3 2/3 2 / 3
( 4 3 π a , 4 3 π a , 4 3 π a ) \left(\frac{4}{3\pi}a,\frac{4}{3\pi}a,\frac{4}{3\pi}a\right)
( 3 π 4 a , 3 π 4 a , 3 π 4 a )
法二




利用 P ( x , y ) d x + Q ( x , y ) d y = ( P ( x , y ) , Q ( x , y ) ) ⋅ ( d x , d y ) P(x,y)\mathrm d x+Q(x,y)\mathrm d y=(P(x,y),Q(x,y))\cdot(\mathrm d x,\mathrm d y) P ( x , y ) d x + Q ( x , y ) d y = ( P ( x , y ) , Q ( x , y ) ) ⋅ ( d x , d y )
( P ( x , y ) , Q ( x , y ) ) ⋅ ( d x , d y ) ≤ P 2 ( x , y ) + Q 2 ( x , y ) ⋅ d s cos θ ≤ P 2 ( x , y ) + Q 2 ( x , y ) ⋅ d s (P(x,y),Q(x,y))\cdot(\mathrm d x,\mathrm d y) \le \sqrt{P^2(x,y)+Q^2(x,y)}\cdot \mathrm d s \cos\theta\le \sqrt{P^2(x,y)+Q^2(x,y)}\cdot \mathrm d s
( P ( x , y ) , Q ( x , y ) ) ⋅ ( d x , d y ) ≤ P 2 ( x , y ) + Q 2 ( x , y ) ⋅ d s cos θ ≤ P 2 ( x , y ) + Q 2 ( x , y ) ⋅ d s
因此
∣ ∫ C P ( x , y ) d x + Q ( x , y ) d y ∣ ≤ max ( x , y ) ∈ C P 2 + Q 2 ⋅ s \left|\int_C P(x,y)\mathrm d x+Q(x,y)\mathrm d y\right|\le \max_{(x,y)\in C}\sqrt{P^2+Q^2}\cdot s
∣ ∣ ∣ ∣ ∫ C P ( x , y ) d x + Q ( x , y ) d y ∣ ∣ ∣ ∣ ≤ ( x , y ) ∈ C max P 2 + Q 2 ⋅ s
利用该结论,可以得到
M = max ( x , y ) ∈ C x 2 + y 2 ( x 2 + y 2 + x y ) 4 = max ( x , y ) ∈ C R 2 ( R 2 + x y ) 4 M=\max_{(x,y)\in C}\sqrt{\frac{x^2+y^2}{(x^2+y^2+xy)^4}}=\max_{(x,y)\in C}\sqrt{\frac{R^2}{(R^2+xy)^4}}
M = ( x , y ) ∈ C max ( x 2 + y 2 + x y ) 4 x 2 + y 2 = ( x , y ) ∈ C max ( R 2 + x y ) 4 R 2
需要 x y xy x y x = R / 2 , y = − R / 2 x=R/\sqrt{2},y=-R/\sqrt{2} x = R / 2 , y = − R / 2 M = 4 R − 3 M=4R^{-3} M = 4 R − 3
0 = lim R → ∞ ∣ I R ∣ ≤ lim R → ∞ 4 R − 3 ⋅ 2 π R = lim R → ∞ 8 π R − 2 = 0 0=\lim_{R\to \infin} |I_R| \le \lim_{R\to \infin}4R^{-3}\cdot 2\pi R=\lim_{R\to \infin}8\pi R^{-2}=0
0 = R → ∞ lim ∣ I R ∣ ≤ R → ∞ lim 4 R − 3 ⋅ 2 π R = R → ∞ lim 8 π R − 2 = 0

首先由于
∂ P ∂ y = f ′ ( x + y ) = ∂ Q ∂ x \frac{\partial P}{\partial y}=f'(x+y)=\frac{\partial Q}{\partial x}
∂ y ∂ P = f ′ ( x + y ) = ∂ x ∂ Q
可以得到积分和路径无关,因此
∫ C f ( x + y ) ( d x + d y ) = ∫ 0 1 f ( t ( a + b ) ) ( d a t + d b t ) = ∫ 0 a + b f ( x ) d x \int_C f(x+y)(\mathrm d x+\mathrm d y)=\int_0^1 f(t(a+b))(\mathrm d at+\mathrm d bt)=\int_0^{a+b}f(x)\mathrm d x
∫ C f ( x + y ) ( d x + d y ) = ∫ 0 1 f ( t ( a + b ) ) ( d a t + d b t ) = ∫ 0 a + b f ( x ) d x

使用格林公式不一定要凑
∂ P ∂ y = ∂ Q ∂ x \frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}
∂ y ∂ P = ∂ x ∂ Q
也可以令两数之差为常数,这里可以注意到
∂ P ∂ y − ∂ Q ∂ x = π \frac{\partial P}{\partial y}-\frac{\partial Q}{\partial x}=\pi
∂ y ∂ P − ∂ x ∂ Q = π
因此
I + ∫ A B ‾ [ φ ( y ) cos x − π y ] d x + [ φ ′ ( y ) sin x − π ] d y = ∬ S π d σ = 6 π 2 I+\int_{\overline{AB}}[\varphi(y)\cos x-\pi y]\mathrm d x+[\varphi'(y)\sin x-\pi]\mathrm d y=\iint_{S} \pi \mathrm d \sigma=6\pi^2
I + ∫ A B [ φ ( y ) cos x − π y ] d x + [ φ ′ ( y ) sin x − π ] d y = ∬ S π d σ = 6 π 2
令 x = ( 2 t + 1 ) π , y = 2 ( t + 1 ) x=(2t+1)\pi,y=2(t+1) x = ( 2 t + 1 ) π , y = 2 ( t + 1 )
∫ 0 1 d ( φ ( y ) sin x ) − π y d x − π d y = 6 π 2 − 2 π \int_0^1 \mathrm d (\varphi(y)\sin x)-\pi y\mathrm d x-\pi \mathrm d y=6\pi^2-2\pi
∫ 0 1 d ( φ ( y ) sin x ) − π y d x − π d y = 6 π 2 − 2 π
所以 I = 2 π I=2\pi I = 2 π

∂ P ∂ y = ∂ Q ∂ x \frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}
∂ y ∂ P = ∂ x ∂ Q
首先,进行代换:
∫ C X d Y − Y d X X 2 + Y 2 = ∫ C ( a x + b y ) ( c d x + d d y ) − ( c x + d y ) ( a d x + b d y ) X 2 + Y 2 = ( b c − a d ) ∫ C y d x − x d y ( a x + b y ) 2 + ( c x + d y ) 2 \int_C \frac{X\mathrm d Y-Y\mathrm d X}{X^2+Y^2}=\int_C\frac{(ax+by)(c\mathrm d x+d\mathrm d y)-(cx+dy)(a\mathrm d x+b\mathrm d y)}{X^2+Y^2}\\=(bc-ad)\int_C \frac{y\mathrm d x-x\mathrm d y}{(ax+by)^2+(cx+dy)^2}
∫ C X 2 + Y 2 X d Y − Y d X = ∫ C X 2 + Y 2 ( a x + b y ) ( c d x + d d y ) − ( c x + d y ) ( a d x + b d y ) = ( b c − a d ) ∫ C ( a x + b y ) 2 + ( c x + d y ) 2 y d x − x d y
取一个半径无穷小的椭圆 ( a x + b y ) 2 + ( c x + d y ) 2 = ε 2 (ax+by)^2+(cx+dy)^2=\varepsilon^2 ( a x + b y ) 2 + ( c x + d y ) 2 = ε 2 X = a x + b y , Y = c x + d y X=ax+by,Y=cx+dy X = a x + b y , Y = c x + d y
I = ( b c − a d ) ∫ C y d x − x d y ε 2 I=(bc-ad)\int_C \frac{y\mathrm d x-x\mathrm d y}{\varepsilon^2}
I = ( b c − a d ) ∫ C ε 2 y d x − x d y
利用
∫ C y d x − x d y = − 2 S \int_C y\mathrm d x-x\mathrm d y=-2S
∫ C y d x − x d y = − 2 S
S = 1 ∣ b c − a d ∣ π ε 2 S=\frac{1}{|bc-ad|} \pi \varepsilon^2
S = ∣ b c − a d ∣ 1 π ε 2
可以得到
∫ C X d Y − Y d X X 2 + Y 2 = 2 π ⋅ sgn ( a d − b c ) \int_C \frac{X\mathrm d Y-Y\mathrm d X}{X^2+Y^2}=2\pi\cdot \operatorname{sgn}(ad-bc)
∫ C X 2 + Y 2 X d Y − Y d X = 2 π ⋅ s g n ( a d − b c )

x F 1 ( x , y ) + y F 2 ( x , y ) = 0 xF_1(x,y)+yF_2(x,y)=0
x F 1 ( x , y ) + y F 2 ( x , y ) = 0
d y d x = − F x F y \frac{\mathrm d y}{\mathrm d x}=-\frac{F_x}{F_y}
d x d y = − F y F x
代入即可得到 d ( x y ) = 0 \mathrm d (xy)=0 d ( x y ) = 0 x y = 2 xy=2 x y = 2

S = ∬ Ω d σ = ∫ C x d y S=\iint_\Omega \mathrm d \sigma=\int_C x\mathrm d y
S = ∬ Ω d σ = ∫ C x d y
对于一个线段:x = x i + λ ( x i + 1 − x i ) , y = y i + λ ( y i + 1 − y i ) x=x_i+\lambda(x_{i+1}-x_i),y=y_i+\lambda(y_{i+1}-y_i) x = x i + λ ( x i + 1 − x i ) , y = y i + λ ( y i + 1 − y i )
∫ C [ x i + λ ( x i + 1 − x i ) ] ( y i + 1 − y i ) d λ = x i ( y i + 1 − y i ) + 1 2 ( x i + 1 − x i ) ( y i + 1 − y i ) = 1 2 ( x i + 1 y i + 1 + x i y i + 1 − x i + 1 y i − x i y i ) \int_C [x_i+\lambda(x_{i+1}-x_i)](y_{i+1}-y_i)\mathrm d \lambda=x_i(y_{i+1}-y_i)+\frac{1}{2}(x_{i+1}-x_i)(y_{i+1}-y_i)\\=\frac{1}{2}(x_{i+1}y_{i+1}+x_iy_{i+1}-x_{i+1}y_i-x_iy_i)
∫ C [ x i + λ ( x i + 1 − x i ) ] ( y i + 1 − y i ) d λ = x i ( y i + 1 − y i ) + 2 1 ( x i + 1 − x i ) ( y i + 1 − y i ) = 2 1 ( x i + 1 y i + 1 + x i y i + 1 − x i + 1 y i − x i y i )
然后发现转一圈之后可以互相抵消,结果就如题所示。




里面有个积分:
∫ 0 1 u 1 + 4 u d u = ∫ 0 1 1 4 ( 1 + 4 u ) 3 / 2 − 1 4 ( 1 + 4 u ) 1 / 2 \int_0^1 u\sqrt{1+4u}\mathrm d u=\int_0^1 \frac{1}{4} (1+4u)^{3/2}-\frac{1}{4}(1+4u)^{1/2}
∫ 0 1 u 1 + 4 u d u = ∫ 0 1 4 1 ( 1 + 4 u ) 3 / 2 − 4 1 ( 1 + 4 u ) 1 / 2
很容易忘。

再复习一下
∫ x 2 + 1 d x = 1 2 ( x x 2 + 1 + ln ( x + x 2 + 1 ) ) \int \sqrt{x^2+1}\mathrm d x=\frac{1}{2} (x\sqrt{x^2+1}+\ln (x+\sqrt{x^2+1}))
∫ x 2 + 1 d x = 2 1 ( x x 2 + 1 + ln ( x + x 2 + 1 ) )




原书的答案错了罢!应该是 8 3 π ( a + b + c ) R 3 \displaystyle \frac{8}{3} \pi (a+b+c) R^3 3 8 π ( a + b + c ) R 3

利用到 ∂ u ∂ n = ( ∂ u ∂ x , ∂ u ∂ y , ∂ u ∂ z ) \displaystyle \frac{\partial u}{\partial \boldsymbol n}=\left(\frac{\partial u}{\partial x},\frac{\partial u}{\partial y},\frac{\partial u}{\partial z}\right) ∂ n ∂ u = ( ∂ x ∂ u , ∂ y ∂ u , ∂ z ∂ u )
对于 (2),高斯公式对第二项求导就是第二项,对第一项求导就是第一项。
对于半空间 x > 0 x>0 x > 0 S S S
∯ S x f ( x ) d y d z − x y f ( x ) d z d x − e 2 x z d x d y = 0 \oiint_S xf(x) \mathrm d y\mathrm d z-xy f(x)\mathrm d z\mathrm d x-e^{2x}z \mathrm d x\mathrm d y=0
∬ S x f ( x ) d y d z − x y f ( x ) d z d x − e 2 x z d x d y = 0
其中函数 f ( x ) f(x) f ( x ) ( 0 , + ∞ ) (0,+\infin) ( 0 , + ∞ ) lim x → 0 + f ( x ) = 1 \displaystyle \lim_{x \to 0^+} f(x)=1 x → 0 + lim f ( x ) = 1 f ( x ) f(x) f ( x )
得到
x y ′ + ( x − 1 ) y + e 2 x = 0 ⇒ y ′ + x − 1 x y = − e 2 x / x xy'+(x-1)y+e^{2x}=0 \Rightarrow y'+\frac{x-1}{x}y=-e^{2x}/x
x y ′ + ( x − 1 ) y + e 2 x = 0 ⇒ y ′ + x x − 1 y = − e 2 x / x
套用公式:
y = e ∫ − P ( x ) d x ( ∫ Q ( x ) e ∫ P ( x ) d x d x + C ) y=e^{\int -P(x)\mathrm d x}\left(\int Q(x) e^{\int P(x)\mathrm d x}\mathrm d x+C\right)
y = e ∫ − P ( x ) d x ( ∫ Q ( x ) e ∫ P ( x ) d x d x + C )
就可以得到 y = 1 x e x ( e x + C ) \displaystyle y=\frac{1}{x}e^x(e^x+C) y = x 1 e x ( e x + C ) C = − 1 C=-1 C = − 1
利用好 n 0 ⋅ d S = d S = ( d y d z , d z d x , d x d y ) \boldsymbol n^0 \cdot \mathrm{d} S=\mathrm{d} \boldsymbol S=(\mathrm{d} y\mathrm{d} z,\mathrm{d} z\mathrm{d} x,\mathrm{d} x\mathrm{d} y) n 0 ⋅ d S = d S = ( d y d z , d z d x , d x d y )
I ( x , y , z ) = ∬ S cos ( r , n ) r 2 d S I(x,y,z)=\iint_S \frac{\cos (\boldsymbol r,\boldsymbol n)}{r^2} \mathrm d S
I ( x , y , z ) = ∬ S r 2 cos ( r , n ) d S
cos ( r , n ) r 2 d S = 1 r 3 ⋅ r ⋅ n ∣ n ∣ d S = 1 r 3 r ⋅ d S = 1 r 3 ( ξ − x , η − y , ζ − z ) ⋅ d S \frac{\cos (\boldsymbol r,\boldsymbol n)}{r^2} \mathrm d S=\frac{1}{r^3} \cdot \frac{\boldsymbol r \cdot \boldsymbol n}{|\boldsymbol n|} \mathrm d S=\frac{1}{r^3} \boldsymbol r \cdot \mathrm d \boldsymbol S=\frac{1}{r^3} (\xi-x,\eta-y,\zeta -z) \cdot \mathrm d \boldsymbol S
r 2 cos ( r , n ) d S = r 3 1 ⋅ ∣ n ∣ r ⋅ n d S = r 3 1 r ⋅ d S = r 3 1 ( ξ − x , η − y , ζ − z ) ⋅ d S
先计算:
∂ ∂ ξ ( ξ − x r 3 ) = 1 ⋅ r 3 − 3 r 3 r ′ ( ξ − x ) r 6 \frac{\partial}{\partial \xi} \left(\frac{\xi-x}{r^3}\right)=\frac{1\cdot r^3-3r^3 r'(\xi-x)}{r^6}
∂ ξ ∂ ( r 3 ξ − x ) = r 6 1 ⋅ r 3 − 3 r 3 r ′ ( ξ − x )
代入 r ′ = ( ξ − x ) / r r'=(\xi-x)/r r ′ = ( ξ − x ) / r
r 2 − 3 ( ξ − x ) 2 r 5 \frac{r^2-3(\xi-x)^2}{r^5}
r 5 r 2 − 3 ( ξ − x ) 2
因此散度为 0,因此只要不包含 ( ξ , η , ζ ) (\xi,\eta,\zeta) ( ξ , η , ζ )
再考虑包含 ( ξ , η , ζ ) (\xi,\eta,\zeta) ( ξ , η , ζ ) ε \varepsilon ε
∬ S 1 ε 2 d S = 4 π \iint_S \frac{1}{\varepsilon^2} \mathrm d S=4\pi
∬ S ε 2 1 d S = 4 π

运用格林公式:
∬ D ∂ 2 f ∂ x ∂ y d x d y = − ∮ C ∂ f ∂ x d x \iint_D \frac{\partial ^2 f}{\partial x\partial y} \mathrm d x\mathrm d y=-\oint_C \frac{\partial f}{\partial x}\mathrm d x
∬ D ∂ x ∂ y ∂ 2 f d x d y = − ∮ C ∂ x ∂ f d x
试用 Lagrange 乘数法求函数 f ( x , y ) = x 3 y f(x,y)=x^3 y f ( x , y ) = x 3 y 3 x + 4 y = 12 ( 0 < x < 4 ) 3x+4y=12(0<x<4) 3 x + 4 y = 1 2 ( 0 < x < 4 )
5 e − 9 / 2 ≤ ∫ C e − x 3 y d s ≤ 5 5e^{-9/2} \le \int_C e^{-\sqrt{x^3y}}\mathrm d s\le 5
5 e − 9 / 2 ≤ ∫ C e − x 3 y d s ≤ 5



也可以计算 x ‾ = 3 \overline{x}=\sqrt{3} x = 3




利用轮换对称性+闭合曲面积分被积函数是1代表曲面的面积。


其实是重积分的内容,拆分成两个曲面计算,利用 d S = 1 + z x 2 + z y 2 d x d y \mathrm d S=\sqrt{1+z_x^2+z_y^2}\mathrm d x\mathrm d y d S = 1 + z x 2 + z y 2 d x d y


过质心的转动惯量。刚体的平行轴定理,在质心处转动惯量最小。
证明:
F ( a , b ) = ( a 2 + b 2 ) ∫ C d s − 2 a ∫ C x d s − 2 b ∫ C y d s + C o n s t F(a,b)=(a^2+b^2) \int_C \mathrm d s-2a \int_C x \mathrm d s-2b \int_C y\mathrm d s+\mathrm{Const}
F ( a , b ) = ( a 2 + b 2 ) ∫ C d s − 2 a ∫ C x d s − 2 b ∫ C y d s + C o n s t
因此
a = ∫ C x d s ∫ C d s , b = ∫ C y d s ∫ C d s a=\frac{\int_C x\mathrm d s}{\int_C \mathrm d s},b=\frac{\int_C y\mathrm d s}{\int_C \mathrm d s}
a = ∫ C d s ∫ C x d s , b = ∫ C d s ∫ C y d s
得到
F ( a , b ) = − ( ∫ C x d s ) 2 + ( ∫ C y d s ) 2 ∫ C d S + ∫ C ( x 2 + y 2 ) d s F(a,b)=-\frac{(\int_C x\mathrm d s)^2+(\int_C y\mathrm d s)^2}{\int_C \mathrm d S}+\int_C (x^2+y^2)\mathrm d s
F ( a , b ) = − ∫ C d S ( ∫ C x d s ) 2 + ( ∫ C y d s ) 2 + ∫ C ( x 2 + y 2 ) d s
还可以进一步证明平行轴定理,假设选择 a ′ , b ′ a',b' a ′ , b ′
F ( a ′ , b ′ ) = ( a ′ 2 + b ′ 2 ) ∫ C d s − 2 a ′ ∫ C x d s − 2 b ′ ∫ C y d s + C o n s t F(a',b')=(a'^2+b'^2)\int_C \mathrm d s-2a' \int_C x\mathrm d s-2b'\int_C y \mathrm d s+\mathrm{Const}
F ( a ′ , b ′ ) = ( a ′ 2 + b ′ 2 ) ∫ C d s − 2 a ′ ∫ C x d s − 2 b ′ ∫ C y d s + C o n s t
代入 ∫ C d s = m \int_C \mathrm d s=m ∫ C d s = m
F ( a ′ , b ′ ) = ( a ′ 2 + b ′ 2 ) m − 2 a ′ a m − 2 b ′ b m + C o n s t F(a',b')=(a'^2+b'^2)m-2a'am-2b'bm+\mathrm{Const}
F ( a ′ , b ′ ) = ( a ′ 2 + b ′ 2 ) m − 2 a ′ a m − 2 b ′ b m + C o n s t
F ( a ′ , b ′ ) − F ( a , b ) = [ ( a ′ − a ) 2 + ( b ′ − b ) 2 ] m = m d 2 F(a',b')-F(a,b)=[(a'-a)^2+(b'-b)^2]m=md^2
F ( a ′ , b ′ ) − F ( a , b ) = [ ( a ′ − a ) 2 + ( b ′ − b ) 2 ] m = m d 2
也就是平行轴定理。


还是需要参数方程代换。



第一种做法是换元:x → 1 + cos t , y → 2 + sin t x\rightarrow 1+\cos t,y\rightarrow 2+\sin t x → 1 + cos t , y → 2 + sin t 6 π 6\pi 6 π
第二种做法利用对称性,注意到圆关于 ( 1 , 2 ) (1,2) ( 1 , 2 )

裸题格林公式。

div F = 2 x y + 3 x y 2 − x y e x y z \operatorname{div} \boldsymbol F=2xy+3xy^2-xye^{xyz}
d i v F = 2 x y + 3 x y 2 − x y e x y z
当 ( x , y , z ) = ( 1 , 1 , 0 ) (x,y,z)=(1,1,0) ( x , y , z ) = ( 1 , 1 , 0 ) 2 + 3 − 1 = 4 2+3-1=4 2 + 3 − 1 = 4

一眼题……



注意分母是 3 / 2 3/2 3 / 2
还可以求出引力场,引力是引力场的梯度。
u ( x , y ) = k ( ( − x ) 2 + ( 3 − y ) 2 ) − 1 2 + C u(x,y)=k((-x)^2+(3-y)^2)^{-\frac{1}{2}}+C
u ( x , y ) = k ( ( − x ) 2 + ( 3 − y ) 2 ) − 2 1 + C
做功是末状态减初状态 u ( 0 , 0 ) − u ( 1 , 0 ) = k 3 − k 10 \displaystyle u(0,0)-u(1,0)=\frac{k}{3}-\frac{k}{\sqrt{10}} u ( 0 , 0 ) − u ( 1 , 0 ) = 3 k − 1 0 k
微分方程 y d x + ( y − x ) d y = 0 y\mathrm d x+(y-x)\mathrm d y=0 y d x + ( y − x ) d y = 0
除以 y 2 y^2 y 2
y d x − x d y y 2 = d ( x y ) \frac{y\mathrm d x-x\mathrm d y}{y^2}=\mathrm d \left(\frac{x}{y}\right)
y 2 y d x − x d y = d ( y x )
d y y = ln ( y ) \frac{\mathrm d y}{y}=\ln (y)
y d y = ln ( y )
因此
x y + ln y = C \frac{x}{y}+\ln y=C
y x + ln y = C



(1)
要记得是三维的形式,d s = x ′ ( θ ) + y ′ ( θ ) + z ′ ( θ ) d θ \mathrm{d} s=\sqrt{x'(\theta)+y'(\theta)+z'(\theta)}\mathrm{d} \theta d s = x ′ ( θ ) + y ′ ( θ ) + z ′ ( θ ) d θ

(2) 正确。
(3) 任意 P , Q P,Q P , Q
(4) 正确。
(5) 正确,观察到
∣ ∬ Σ ( P , Q , R ) ⋅ ( d y d z , d z d x , d x d y ) ∣ ≤ ∣ ∬ Σ P 2 + Q 2 + R 2 ⋅ d S ∣ ≤ M S \left|\iint_\Sigma (P,Q,R) \cdot (\mathrm{d} y\mathrm{d} z,\mathrm{d} z\mathrm{d} x,\mathrm{d} x\mathrm{d} y)\right| \le \left|\iint_\Sigma \sqrt{P^2+Q^2+R^2} \cdot \mathrm d S\right|\le MS
∣ ∣ ∣ ∣ ∬ Σ ( P , Q , R ) ⋅ ( d y d z , d z d x , d x d y ) ∣ ∣ ∣ ∣ ≤ ∣ ∣ ∣ ∣ ∬ Σ P 2 + Q 2 + R 2 ⋅ d S ∣ ∣ ∣ ∣ ≤ M S