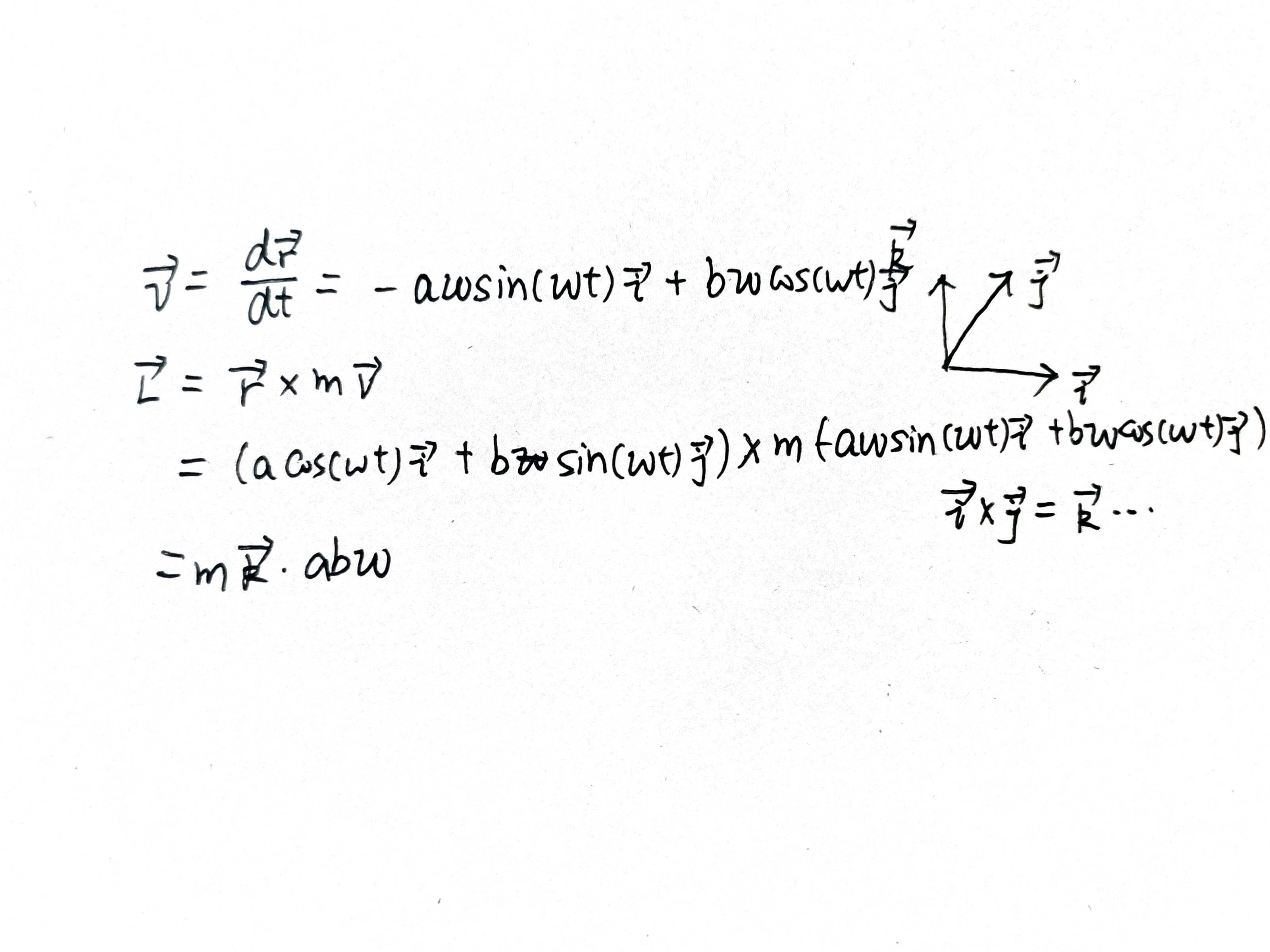动量定理 动量守恒定律
p=mvp=Mvc
牛顿第二定律:
F=dtd(mv)⇒F=mdtdv=ma
恒力的冲量:I=F(t2−t1)。
变力的冲量:I=∫t0tF⋅dt。(是否可行)
因此,质点在运动过程中,所受合外力的冲量等于质点动量的增量。质点动量定理
I=∫0tFdt=p−po=mv−mv0
冲击、碰撞问题中估算 平均冲力。
作用时间短,变化复杂,无法通过力计算冲量。
F=ΔtI=t−t01∫t0tF⋅dt=t−t0p−p0
适用于 惯性系,在非惯性系中,只有添加惯性力的冲量后才成立。

∑NΔt=mv1sinθ−∑μNΔt=mv2−mv1cosθ
遇到斜面的问题,还要注意运动方向的改变,如果只用分析水平方向的动量守恒,也要注意水平方向分速度的改变。

需要注意不要忘了重力。
动量守恒定律
当 ∑Fi=0 时,p=∑mivi=const.
质量为 M 的平板车开始时静止于光滑直轨道上,车上 n 个质量均为 m 的人相对车以速度 u 向后跳离。
-
若所有人同时跳离,平板车的最终速度为多少?
根据动量守恒定律(一开始动量为0,则改变状态后动量为0)
0=Mv+nm(−u+v)⇒v=M+nmnmu
-
若一个一个地跳离,平板车的最终速度又为多少?
第一个人跳离时,有:
0=[M+(n−1)m]v1+m(−u+v1)⇒v1=M+nmmu
第二个人跳离时,有:
[M+(n−1)m]v1=[M+(n−2)m]v2+m(−u+v2)⇒v2−v1=M+(n−1)mmu
第三个人跳离时,有:
[M+(n−2)m]v2=[M+(n−3)m]v3+m(−u+v3)⇒v3−v2=M+(n−2)mmu
因此
vn=k=1∑nM+kmm>M+nmnm
启发:求出 vi 不好处理,可以考虑差分的形式,当然也可以归纳得出。
质点系动量
设有 N 个质点构成一个系统,第 i 个质点的质量为 mi,内力 fi,外力 Fi,初速度 vi0,末速度 vi。
由质点动量定理:
∫t0t(Fi+fi)dt=mivi−mivi0
一对内力做功不一定为 0。
其中 ∑fi=0。
因此
∫t0t∑Fidt=p−p0=Δp
微分式:
∑Fi=dtdp
形式上,与单个质点动量定理相同,但内涵有差别。
当 ∑Fi=0,p=∑mivi 为常量。
- 动量守恒是指系统动量总和不变,但系统内各个质点的动量可以变化, 通过内力进行传递和交换。
- 当外力作用远小于内力作用时,可近似认为系统的总动量守恒。(如:碰撞、打击等)
质量分别为 m1 和 m2 的小孩在光滑的平面上彼此拉对方。设开始时静止,相距 l。问他们在何处相遇?
m1v1+m2v2=0
不能写作 m1v1=m2v2。
在任意时刻
x1=x10+∫0tv1dtx2=x20+∫0tv2dtx20−x10=∫0t(1+m2m1)v1dtl=∫0t(1+m2m1)v1dtx=x1=x10+∫0tv1dt=m1+m2m1x10+m2x20
以质量为权重的位置。
炮车的质量为 M,炮弹的质量为 m。若炮车与地面之间有摩擦,摩擦系数为 μ,炮弹相对炮身的速度为 u,求炮身相对地面的反冲速度 v。
对系统分析
在 τ 的时间内,
∫0τ∑Fidt=∫0τ(Mg+mg+N+f)dt=Δp=Mv+m(v+u)−0
分别对 x,y 方向分析。注意 ∫∣f∣=μ∫∣N∣。
则可以得到
∫0τfdt=−Mv+m(−v+ucosθ)∫0τ(N−Mg−mg)dt=musinθ⇔∫0τNdt=musinθ
注意到 (Mg+mg)τ 为小量(相对于等号右边的 musinθ),因此可以略去。
得到
v=M+mmu(cosθ−μsinθ)
如果没有摩擦,相当于水平方向动量守恒。
如果水平发射炮弹,相当于碰撞的逆过程。
如果 cotθ=μ 或者 cotθ<μ,炮车会发生自锁现象,不会移动,当然不会速度反向……

质心 质心运动定理
质心
考虑两个质点组成的孤立体系。
P=m1v1+m2v2=m1dtdr1+m2dtdr2=dtd(m1r1+m2r2)=(m1+m2)dtd(m1+m2m1r1+m2r2)=Const
定义:
rc:=m1+m2m1r1+m2r2vc:=dtdrcM:=m1+m2
则
P=Mvc
推广到 n 个粒子系统。
rc:=Mi∑mi∑imiri
对于连续分布的物体:
rc=limmax{Δmi}→0∑i=1NΔmilimmax{Δmi}→0∑i=1NΔmiri=∭τdm∭τrdm
其中
dm=ρdV=σdS=λdl
质心运动定理
质心运动定理:质心的运动等同于一个质点的运动,这个质点具有质点系的总质量,它受到的外力为质点系所受的所有外力的矢量和。
Mvc=i∑mivi
所有的参考系都成立。参考系存在质心上。
rc≡0⇒vc=0⇒i∑mivi=0
ac=dtdvc=dtd(i∑mivi/M)=i∑Fi/M
F=Mac
只描述平动。
适用于 惯性系。
若 ac=0,则质心系为惯性系。
若 ac=0,质心系为非惯性系。

动量守恒、功能原理、角动量定理在质心系成立。质点系相对惯性系的运动可以分解为:随质心的运动+相对质心的运动。
vi=vc+vi′
i∑21mivi2=21Mvc2+=0i∑vc⋅mivi′+资用能i∑21mivi′2
只有在质心系中成立。
(M∑imivi′)⋅vcM
代表在质心系中质心的速度。换句话说,在质心系中系统总动量为 0。
孤立系中,合外力的冲量为 0,则 21Mvc2=Const,则资用能为常数。
如果 ∑i21mivi2 为固定值,为了使 ∑i21mivi′2 最大,需要让 vc 最小,对撞。




质心的特性
质心系的动量为0。内力的冲量和为0。内力的力矩和为0。
速度、加速度的分解:相对于质心的速度、加速度+质心的速度、加速度。
动量的分解:没有分解,就是质心整体的动量。
角动量的分解:相对于质心的角动量+质心的动量。
质心系下功能原理/角动量定理守恒是适用的。
碰撞问题
碰撞是自然界中十分普遍的现象。
两者有可能结合在一起,或产生新的成分。
- 相互作用强。
- 力的形式复杂
- 无法直接测量和记录碰撞过程
处理碰撞的物理定律是动量守恒。
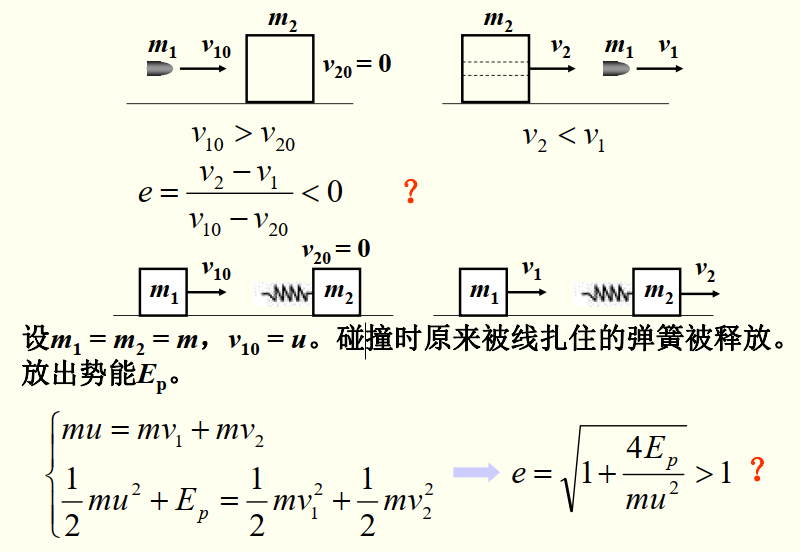
弹性碰撞 碰撞后的物体和碰撞前相同,而且物体内部状态无变化。能量相同。碰撞后物体的形变可以完全恢复,且碰撞前后系统的总机械能守恒。
非弹性碰撞 碰撞后的物体与碰撞前不相同,或物体内部状态有变化。碰撞后物体的形变只有部分恢复,系统有部分机械能损失。
完全非弹性碰撞 碰撞后物体的形变完全不能恢复,两物体合为一体一起运动,沿着碰撞方向的速度相等。系统有机械能损失。
微观粒子:碰撞 ⇔ 散射
{m1v10+m2v20=m1v1+m2v221m1v102+21m2v202=21m1v12+21m2v22
{v1=m1+m2(m1−m2)v10+2m2v20v2=m1+m2(m2−m1)v20+2m1v10
- m1=m2 时,交换速度。
- v20=0 且 m2≫m1 撞墙调转运动方向。
- v20=0 且 m2≪m1,则 v1≈v10,v2≈2v10。
一般情况的非弹性碰撞,碰撞后两球的分离速度 (v2−v1) 与碰撞前两球的接近速度 (v10−v20) 成正比。比值由材料决定。恢复系数的定义:沿着碰撞方向的前后相对速度之比。
e=v10−v20v2−v1
弹性碰撞 e=1,非弹性碰撞 0<e<1,完全非弹性碰撞 e=0。
碰撞后两球的速度
v1=v10−m2m1+m2(1+e)(v10−v20)v2=v20+m1m1+m2(1+e)(v10−v20)
机械能损失
ΔEk=−21(1−e2)m1+m2m1m2(v10−v20)2
当 e=0,代表完全非弹性碰撞,令折合质量
μ=m1+m2m1m2
ΔEk=−21μ(v10−v20)2
接近速度。
对于二维碰撞,如果给出散射角,就能唯一确定。
恢复系数的物理意义:
e=v10−v20v2−v1=压缩阶段冲量恢复阶段冲量
压缩阶段
m2I1=v−v20m1I1=v10−vI1(m11+m21)=v10−v20
恢复阶段
I1(m11+m21)=v2−v1
e<0,e>1 的情况

质心系中,在碰撞前后两质点的动量始终大小相等,方向相反。
光滑桌面上,质量为 m1 的小球以速度 u 碰在质量为 m2 的静止小球上,u 与两球的连心线成 θ 角(称为斜碰)。设两球表面光滑,它们相互撞击力的方向沿着两球的连心线(也就是说,m1 球给 m2 球的动量沿着连心线方向,m2 速度的方向已知,给了我们建系的提示),已知恢复系数 e。求碰撞后两球的速度。
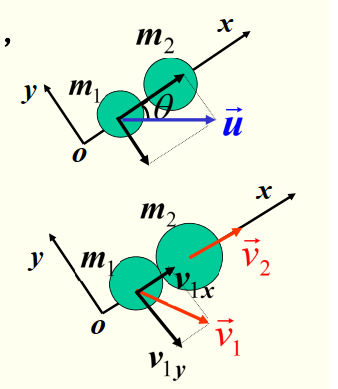
利用 x,y 方向动量分别守恒(其中 y 方向速度不变,可以隔离分析,只用分析一个一维的运动)
m1v1x+m2v2=m1ucosθ−m1v1y=−m1usinθ
恢复系数
e=v10−v20v2−v1=ucosθv2−v1x
**
首先得到 vx=v0,vy=2gh,碰撞后(以竖直向上为正方向)
vM=m+Mm−Mvyvmy=m+M2mvy
然后使用机械能守恒,以 M 初始位置为零势能点,然后可以忽略 M 的重力,得到
21MvM2=21kx2
因此,
x=kMvM=m+M2mk2Mgh
只发生一次碰撞,应该正好在板子的边缘离开板子。
变质量物体的运动
运动主体+抛(吸)物体
在 t 时刻动量为 P(t),在 t+Δt 时刻动量为 P(t+Δt)。则 ΔP=P(t+Δt)−P(t)=∑FΔt。
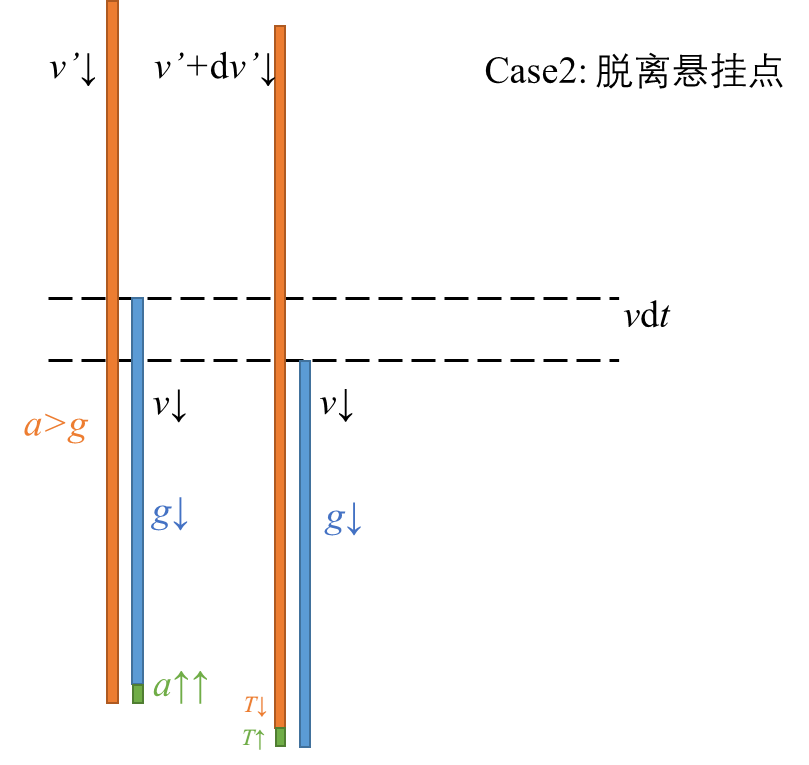
提绳子,线密度 λ。t 时刻提到 x,速度为 v,在 t+dt,多提起来 vdt 长度的绳子。
Fdt−xλgdt=λ(x+vdt)(v+dv)−λxv
火箭、提链子。
设 t 时刻,火箭质量为 m1,速度为 v,在 dt 时间内,喷出气体为 dm2,喷气相对火箭的速度(喷气速度)为 u 向下。
−P(t)+P(t+dt)=F外⋅dt
研究喷气的动量变化:
(下一时刻火箭的速度v+dv−u)dm2−vdm2≈−udm2
由动量定理:
(F+dm2g)dt=Fdt=−udm2
反作用力
FP=udtdm2
对于火箭和喷气组成的系统
Fdt=(m1−dm2)(v+dv)+dm2(v+dv−u)−m1v=m1dv−udm2
因此推出:
F=m1dtdv−udtdm2=====dm1=−dm2m1dtdv+udtdm1
火箭的速度公式,如果只记重力,F=−m1g,两边同时除以 m1,分离变量:
∫0t−gdt=∫0tdtdvdt+∫0tum1dtdm1dt−gt=v(t)−v(0)+ulnm(0)m(t)v=ulnm1m10−阻力gt
如果不计重力,得到
v=ulnm1m10
如何最大化速度,
v_\max = u \ln \frac{m_{10}}{m_{1\min}}
问题相当于,原来静止 m10 的物体,一份一份地以相对速度 u 射出物体的部分,求物体质量为 m1 时可能达到的最大速度。需要分的越小越好。
希望最小化剩下的质量。
提高火箭速度的途径
- 增加 u。
- 增加 m10/m1min。但是由技术方面的限制。
多级火箭
v=i∑ulnNi=uln(i∏Ni)
绳子、链条运动的问题
质量为 M 的运至链条,全长为 L,手持其上端,使其下端刚好碰到桌面。然后放手让它自由下落到桌面上,如图。求链条落到桌面长度为 l 时,桌面所受链条作用力的大小。
令 λ=M/L,
(mg−N)dt=−λ(L−l)v+λ(L−l−vdt)(v+gdt)
得到
N=L3Mgl
质点的角动量 角动量守恒定律
角动量(动量矩)
由于动量 p=mv 不能描述转动问题。例如一个轻杆连接两个物体,这时候动量恒为 0。

引入质点关于参考点 O (参考系中不动点)的角动量。
L:=r×p=r×mv
大小:
L=rmvsinθ
分量式:
L=r×p=∣∣∣∣∣∣ixpxjypykzpz∣∣∣∣∣∣
因此,
Lx=ypz−zpy=m(yvz−zvy)

质点角动量定理
类比
Ek=21mv2dtdEk=F⋅v(功率)p=mvdtdp=F(力)dtdL=dtd(r×mv)=r×dtd(mv)+vdtdr×mv=r×dtd(mv)=r×F
合力对 同一参考点 O 的力矩。
M:=r×FM=Fd=Frsinθ
角动量是力矩的时间累积效应。
M=r×F=dtdL
微分形式,表示在 dt 时间的变化
Mdt=dL
积分形式
r×I=∫t0tMdt=∫L0LdL=L−L0
∫t0tMdt 称为合力矩在 t0→t 时间内的 冲量矩。
角动量守恒定律
当 M=0,比如 F=0,$\boldsymbol F $ 过 O 点:有心力(如行星受中心恒星的万有引力)
L=Const
轨道在同一个平面内。
在中心力场中,关于力心的角动量守恒:
L=mvrsinα=mdt∣dr∣rsinα=2mdt21r∣dr∣sinα三角形的高=2mdtdS
得到 开普勒第二定律 面积定律
dtdS=2mL0
常量,只和运动的行星有关。
质点对轴的转动定律
Mz=0⇒Lz=Const
如果外力使质点变换轨道,由角动量守恒得到
R2mv2=R1mv1⇒v2=R2R1v1
质点系的角动量
作用于质点系的力矩
M=i∑Mi=i∑ri×Fi
重力矩
Mg=i∑ri×(mig)=rc×mg
取质心为轴,重力的力矩为 0。
内力矩
一对力力的方向沿两者连线上,因此
Mij=ri×fij+rj×fji=(ri−rj)×fij=rij×fij≡0
dtdL=i∑ri×外力Fi=M
质点系角动量守恒的条件:
- 外力为 0.
- 每个外力矩为 0.
- 外力矩加起来为 0.
质点系的动量守恒和角动量守恒是独立的,可以同时满足。
质心系的角动量定理
L=i∑ri×mivi
与惯性系中形式完全相同,但是无论质心系做匀速平动还是加速平动都成立。
[例4-12] 发射宇宙飞船去考察一质量为 m1 、半径为 R 的行星, 当飞船静止于距行星中心 4R 处时, 以速度 v0 发射一 质量为 m2(m2 远小于飞船质量) 的仪器, 要使仪器恰好掠着 行星的表面着陆, θ 角应是多少? 着陆滑行初速度 v 多大?
运用 角动量守恒 和 系统机械能守恒 定律。
[例2-30] 将一质点沿一个半径为 r 的光滑半球形碗的内面 水平地 投射, 碗保持静止, 如图, 设 v0 是质点恰好能达到 碗口所需的初速率. (1) 试说明质点为什么能到达碗口?
(2) 求 v0 与 θ0 的关系。 ( θ0 是质点的初始角位置, o 为球心 )
当 Ncosθ0>mg 时,小球能向上加速。
临界条件:
Nsinθ0=mrsinθ0v02Ncosθ0=mg⇒v0=grcosθ0sin2θ0
恒力的力矩沿着这个力的方向为 0,因此分角动量守恒。这里,在 z 轴角动量守恒。
角动量守恒:
mv0rsinθ0=mvr
[例2-32] 如图所示, 质量为 m 的飞船绕质量为 M 的地球作匀速 圆周运动, 轨道半径为 3R ( R 为地球半径), 它的运行速率 v0 为 多少?飞船在此处要将它的运动速度至少增加到 v1 为多少时, 才能飞离地球? 若飞船在 3R 处将速度增加到 v1 后关闭发动机, 在离地心为 12R 处, 它的切向加速度分量 at 为多少?该处轨道的 曲率半径 ρ 为多少 (用地球半径 R 以及地球表面附近的重力加速 度 g 表示结果)?
在地面处:
GR2Mm=mgg=GR2M
飞船在 3R 处绕地球做匀速圆周运动,得到
m3Rv02=G(3R)2mM=9mg
得出 v0。
为了脱离地球,系统机械能至少为零。
21mv12−G3RMm=0⇒v1=32Rg
从 3R 到 12R,系统机械能守恒。
21mv22−G12RMm=0⇒v2=6Rg
实际上,若机械能为零,应该做抛物线运动。
在此过程中,飞船相对于地心角动量守恒:
mv1⋅3R=mv2⋅12Rsinθ⇒sinθ=21
需要把飞船的加速度沿速度方向和垂直速度方向分解。
∣a∣=G(12R)2M=144g
所以
at=−acosθ=−2883gan=asinθ=288gρ=v22/an=48R
质量为 M 的静止粒子 A 与质量为 m,具有速度的粒子 B 碰撞,实验发现,当 B 的动能小于某个数值时,A,B 发生非弹性碰撞,只有当 B 的动能大于此值时,A,B 发生非弹性碰撞,此时 B 将吸收数值为 ΔE 的固定能量。
计算 B 所应具有的这一动能值。
质心速度不变
vc=m+Mmv0
系统能量守恒:
21mv02=const21(m+M)vc2+21mv2+21MV2+ΔE
为了使 v0 最小,需要
21mv2=21MV2=0
因此,
Ek=2(m+M)m2v02+ΔE
同轴圆筒 (Ma、Mb) 均可自由转动, 外筒开始静止。内筒开有许多小孔,内表面散布着一薄层沙 (M0), 以 ω0 匀速转动,沙飞出并附着在 外筒内壁。单位时间喷出沙的质量为 k, 忽略 沙的飞行时间,求 t 时刻两筒角速度。
内筒仅仅是把沙子甩出,所以角速度不变。利用沙子和外筒角动量守恒,可以得到:
kta2ω0=(Mb+kt)b2ωb
因此,
ωb=(Mb+kt)b2kta2ω0
两球的质量均为 m,轻绳,光滑水平面,求运动规律及绳中张力。
首先,分析质点系的平动,得到水平方向守恒,也就是
mv0=2mvc⇒vc=21v0
然后再在质心系中分析,得到系统相对质心角动量守恒,为了处理角速度:
mv02l=m(2l)2ω+m(2l)2ω⇒ω=lv0
为什么不选择相对于其他的点角动量守恒,也可以得到:
mv0l=ml2ω⇒ω=lv0
所以可以选择质心以外的点分析。
绳中的张力:
T=m2lω2=21mlv02
三球质量均为 m,轻杆,光滑水平面,对心弹性碰撞,分析其运动情况。

a,b 被轻杆束缚,因此选择 ab 作为一个整体分析。其质心位于两球连线的中央。
因此动量守恒,得到:
mv0=mv+2mvc
cb 两球的作用力沿两球连线方向,碰撞之后 c 运动仍然在 cb 连线这条直线上。
设 ab 杆相对于质心的角速度为 ω,则相对于 c,va=vb=ω2l,r=2l,因此总角动量为
2m(2l)2ω
因此,系统角动量守恒就是说:
mv02lsin45∘=mv2lsin45∘+2m(2l)2ω
系统机械能守恒就是:
21mv02=21mv2+21(2m)vc2+21(2m)(2l)2ω2
为什么不选择 abc 整体的质心分析,因为 c 不受束缚,质心的位置难以确定。
处理天体运动,一般需要机械能守恒+角动量守恒。

习题

(2) 问使用整体法
(F+λlg)dt=p(t+dt)−p(t)
p(t)=2l−21gt2


注意是相对于炮车。
3-7

需要注意相对运动。
3-8

3-10
船在运动过程中受到的阻力和船相对于水的速度成正比,也就是说
I=∫fdt=∫−kvdt=−kΔx
其中 Δx 是船相对于水运行的距离。
- 一开始人、船都是静止的,到最后也是整体静止。
- 需要分析人停下的瞬间,因为这个时候速度发生了突变,整体是动量守恒的。
还可以利用牛二,设 f′ 为人船之间的摩擦力。
Mdtdv=−kv−f′mdtd(v+u)=f′
得到(瞬时的摩擦力)
f′=−kvM+mm
人瞬间停下,系统的总动量不变,因此
P=m1(v+u)+Mv=−kx1
则 x2=−x1,Δx=0。
如果需要分析瞬时的摩擦力与速度的关系,就可以用这种方法。
3-11

在 t 时刻,
I=Fdt=(m(t)−qdt)(v+dv)+qvdt−m(t)v
得到
Fdt=m(t)dv
dv=m0−qtdtF
v=qFln(m0−qtm0)
3-12

利用 Fdt=dp火箭=dp气体=vdm,因此得到 dm/dt=Mg/v。
3-13

利用全过程动量守恒和 t 到 t+dt 时间内动量守恒:
m0v0=mtvt=(mt+ρSvdt)(vt+dv)
得到
−ρSv3dv=m0v01dt
积分即可得到
v=m02+2m0v0ρStm0v0
3-20

W=∫F1dl=∫OPcv⋅dl=∫OPcvdl=cv⋅πR
I=∫F1dt=∫cvdt=c∫dx
3-22

由于地面光滑,所以水平速度不变,保持 v0。
e=v1−00−(−v2)
tanθ2=v2v0tanθ1=v1v0
tanθ1=etanθ2
**3-25

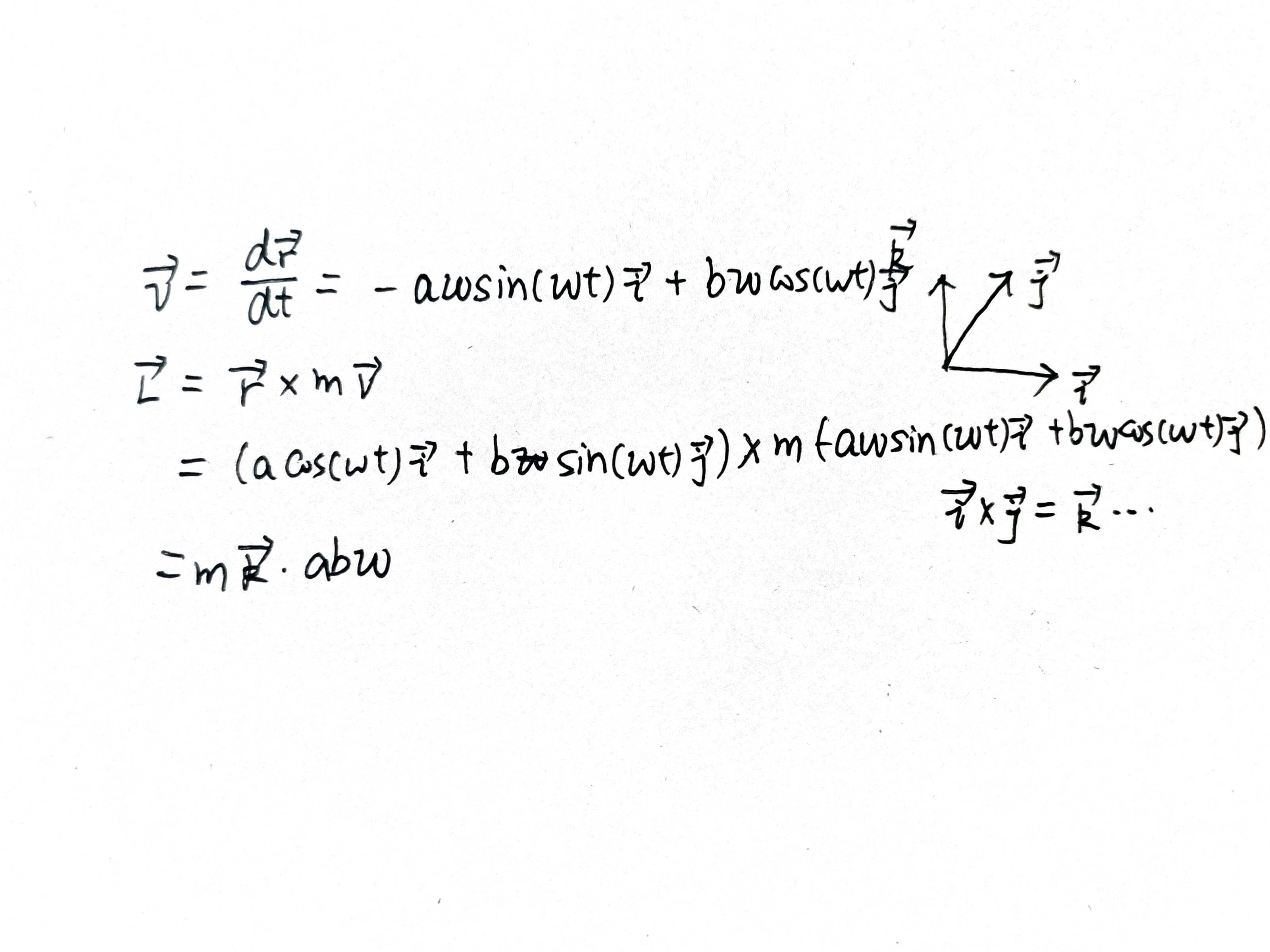
注意矢量叉乘的计算。
3-28

速度使用能量守恒计算,横向速度 vθ 使用角动量守恒计算。
4-7
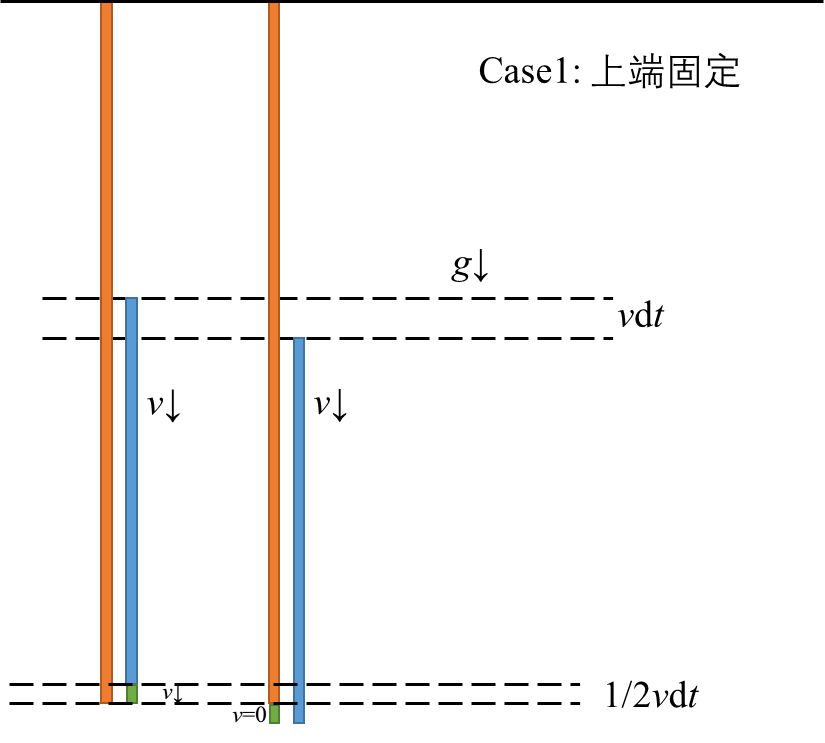
如图所示,一质量为 m 的匀质链条,长为 L,手持其上端,下端与桌面接触。现使链条自静止释放落于桌面,试从下述三种不同的规律出发,计算链条下落 s 距离时桌面对链条的作用力:
动量规律
一般都是在 Δt 的时间内分析。根据质点系动量定理
[Lm(y+dy)g−FN]dt=0−vdm=0−Lmvdy
两个高阶小量相乘可以约掉,因此
Lmgy−FN=−Lmv2=−Lm2gy
得到
FN=3Lmgs
质心运动规律
取整个链条分析分析,先求出其质点。
取沿桌面竖直向上为 y 轴正方向。
yc=mLmy未掉落绳子重量⋅2y其质心+(m−Lmy)剩下质量⋅0选取桌面为0点=2Ly2
质心速度
vc=−Lyv(掉落速度)
质心加速度
ac=L1v2+Lya(掉落加速度=−g)
根据质心运动定理 FN−mg=mac。
得到
FN=3Lmgs
4.5

4.7


4.8

4.9


使用牛顿运动定律。注意 vC 只是标量,因此
ac=dtdvc=dtdvcet+2L+rω⋅ωen=2L+rω2
根据质心运动定律,
T=mac=2LM(L2−r2)ω2
也可以利用质心运动定律,在 Δt 的时间内,
I=TΔt=Δp=mΔθ⋅2L+rω=m2L+rω2Δt
4.10
19-2

19-5
质量为 m 的质点受到两个力的作用,一个是有心力 F1=f(r)er,另一个是摩擦力 F2=−λv(常数 λ>0),其中 v 是质点的速度。若初始时刻该质点对 r=0 的角动量为 L0,求以后各时刻质点角动量的大小。
有心力力矩为 0,这里积分情况比较复杂,难以分析,我们使用微分方程的形式。
M=dtdL
−λv×r=dtdL
两边取矢量模长
−rλvsinθ=dtdL
因为 L=mrvsinθ,所以,观察到相似的形式,得到
−λmL=dtdL
因此
L=L0e−mλt
21-10

注意角动量的定义
L=mv×rL=mvrsinθ
摆球对圆心的角动量大小为
m⋅Rω⋅R=mR2ω
对时间的一阶导数为 0,因为合力的方向向心。
摆球对悬挂点的角动量大小为
m⋅Rω⋅r⋅1=mrRω
对时间的一阶导数可以通过力矩计算,大小是 mgR。
其他的方法:纯数学的方法,得到位矢 r 关于时间的表达式:
rO′=Rcosωti+Rsinωtj−hkrO=Rcosωti+Rsinωtjv=−Rωsinωti+Rωcosωtj
LO=rO×(mv)=mωR2k
LO′=rO′×(mv)=mωR2k+mωRh(sinωtj−cosωti)
∣LO′∣=mωR⋅R2+h2=mωrR
对时间的一阶导数
∣∣∣∣dtdLO′∣∣∣∣=mω2Rh
这里,我们发现其实上 g=ω2h。
如果知道角动量对时间的导数就代表合力矩的物理意义,就可以计算的更快。