分析受力,分析运动找 约束 ,建系列方程,解之。
明确运动的物体。
考察物体所受力。
运动的参考系。
各个质点所受的力。
运动方程(分量方程)
几何关系。
近似。

对于 d θ \mathrm d \theta d θ
d N = T d θ − d F ∗ \mathrm d N=T\mathrm d \theta-\mathrm d F^*
d N = T d θ − d F ∗
d F ∗ = d θ 2 π m r 2 ω 2 \mathrm d F^*=\frac{\mathrm d \theta}{2\pi} mr_2 \omega^2
d F ∗ = 2 π d θ m r 2 ω 2
d N = ( 2 π k ( r 2 − r 1 ) − m r 2 ω 2 2 π ) d θ \mathrm d N=\left(2\pi k(r_2-r_1)-\frac{mr_2\omega^2}{2\pi}\right)\mathrm d \theta
d N = ( 2 π k ( r 2 − r 1 ) − 2 π m r 2 ω 2 ) d θ
得到整体的支持力 N N N
N = ( 2 π k ( r 2 − r 1 ) − m r 2 ω 2 2 π ) 2 π N=\left(2\pi k(r_2-r_1)-\frac{mr_2\omega^2}{2\pi}\right)2\pi
N = ( 2 π k ( r 2 − r 1 ) − 2 π m r 2 ω 2 ) 2 π
μ N ≥ m g ⇒ ⋯ \mu N \ge mg \Rightarrow \cdots
μ N ≥ m g ⇒ ⋯

由于纯滚动的定义:v c = R ω v_c=R\omega v c = R ω a c = R β a_c=R\beta a c = R β O O O P P P
a P = a c + R β = 2 R β a_P=a_c+R\beta=2R\beta
a P = a c + R β = 2 R β
对于圆筒(受摩擦力)列质心运动定理
F − f = M a c F-f=Ma_c
F − f = M a c
对于小物块,列牛二
m g − T = m a mg-T=ma
m g − T = m a
J β = R T + R f J\beta=RT+Rf
J β = R T + R f
a c = 4 m 3 M + 8 m g a_c=\frac{4m}{3M+8m}g \quad
a c = 3 M + 8 m 4 m g
注:摩擦不一定是要相对运动产生,这道题中,圆筒和地面的接触点没有相对运动,但是也产生了摩擦力 其实发现摩擦力的方向和拉力是相同的,也就是摩擦力促进了圆筒的运动。
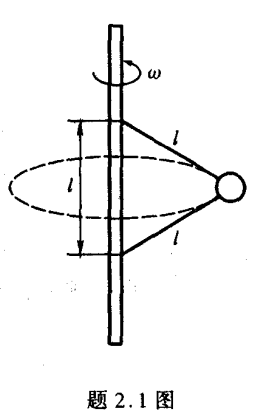
质量为 M M M L L L ω \omega ω O O O r r r
m = ( L − r ) M L m=(L-r)\frac{M}{L}
m = ( L − r ) L M
质心距离原点 O O O
1 2 ( L + r ) \frac{1}{2}(L+r)
2 1 ( L + r )
张力:
T = m a = ( L − r ) M L ⋅ 1 2 ( L + r ) ω 2 T=ma=(L-r)\frac{M}{L}\cdot \frac{1}{2}(L+r)\omega^2
T = m a = ( L − r ) L M ⋅ 2 1 ( L + r ) ω 2
两物体拉绳
B : N + T B + f + G = m B a B A : G A + T A = m A a A B:\boldsymbol N+\boldsymbol T_B+\boldsymbol f+\boldsymbol G=m_B \boldsymbol a_B\\
A:\boldsymbol G_A+\boldsymbol T_A= m_A \boldsymbol a_A
B : N + T B + f + G = m B a B A : G A + T A = m A a A
附加约束,T A = T B , a A = a B , f = μ N \boldsymbol T_A=\boldsymbol T_B,\boldsymbol a_A=\boldsymbol a_B,\boldsymbol f=\mu \boldsymbol N T A = T B , a A = a B , f = μ N
讨论……
讨论雨滴下落过程中收到空气粘滞力作用时的运动规律。
m g + f = m a f = − k v mg+f=ma\\f=-kv
m g + f = m a f = − k v
⇒ m g − k v = m d v d t \Rightarrow mg-kv=m \frac{\mathrm d v}{\mathrm dt}
⇒ m g − k v = m d t d v
d v g − k m v = d t − m k ln ( g − k m v ) = t + C \frac{\mathrm d v}{g-\frac{k}{m} v}=\mathrm d t
\\ -\frac{m}{k}\ln (g-\frac{k}{m} v)=t+C
g − m k v d v = d t − k m ln ( g − m k v ) = t + C
由于一开始运动,C = 0 C=0 C = 0
v = m g k ( 1 − e − k m t ) v=\frac{mg}{k} (1-e^{-\frac{k}{m}t})
v = k m g ( 1 − e − m k t )
Terminal Velocity. 弛豫时间。
Φ Φ ˙ = τ \frac{\Phi}{\dot{\Phi}}=\tau
Φ ˙ Φ = τ
{ q E + q v y B = m d v x d t q v x B = m d v y d t \left\{\
\begin{matrix}
qE+qv_yB=m \frac{\mathrm d v_x}{\mathrm d t}\\
qv_xB=m\frac{\mathrm d v_y}{\mathrm d t}
\end{matrix}
\right.
{ q E + q v y B = m d t d v x q v x B = m d t d v y
令 ω = q B / m , γ = q E / m \omega=qB/m,\gamma=qE/m ω = q B / m , γ = q E / m
{ v ˙ x = γ + ω v y v ˙ y = ω v x \left\{\
\begin{matrix}
\dot{v}_x=\gamma + \omega v_y\\
\dot{v}_y=\omega v_x
\end{matrix}
\right.
{ v ˙ x = γ + ω v y v ˙ y = ω v x
v y = ( v ˙ x − γ ) / ω v x = v ˙ y / ω v_y=(\dot{v}_x-\gamma)/\omega\\
v_x=\dot{v}_y/\omega
v y = ( v ˙ x − γ ) / ω v x = v ˙ y / ω
⇒ { v ¨ y + ω 2 v y = ω γ \Rightarrow\left\{\
\begin{matrix}
\ddot{v}_y+\omega^2v_y=\omega \gamma
\end{matrix}
\right.
⇒ { v ¨ y + ω 2 v y = ω γ
考虑 几何关系 ,可以得出 A , B A,B A , B
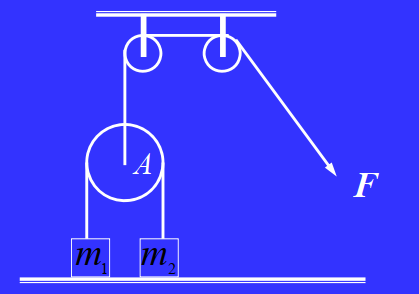
分析:1、几何约束关系。轻绳不可伸长。2、受力、绳拉力和环支持力(沿法向方向)
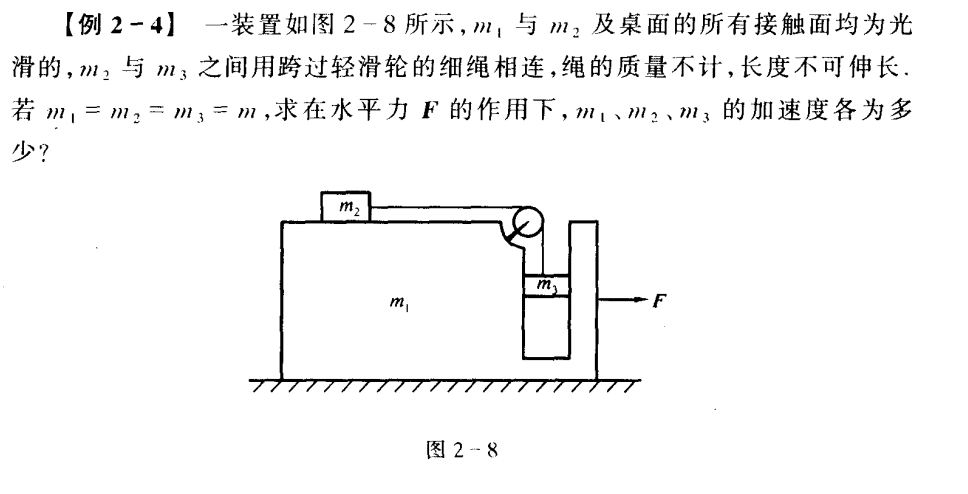
已知:轻滑轮 A A A m 1 , m 2 m_1,m_2 m 1 , m 2 F F F A A A m 1 , m 2 m_1,m_2 m 1 , m 2
轻绳的约束关系:设 m 2 m_2 m 2 A A A a \boldsymbol a a m 1 m_1 m 1 A A A − a -\boldsymbol a − a
轻滑轮一定受力平衡。设绳上拉力为 T T T
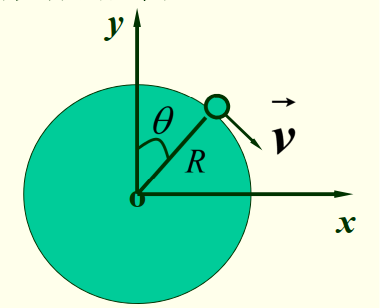
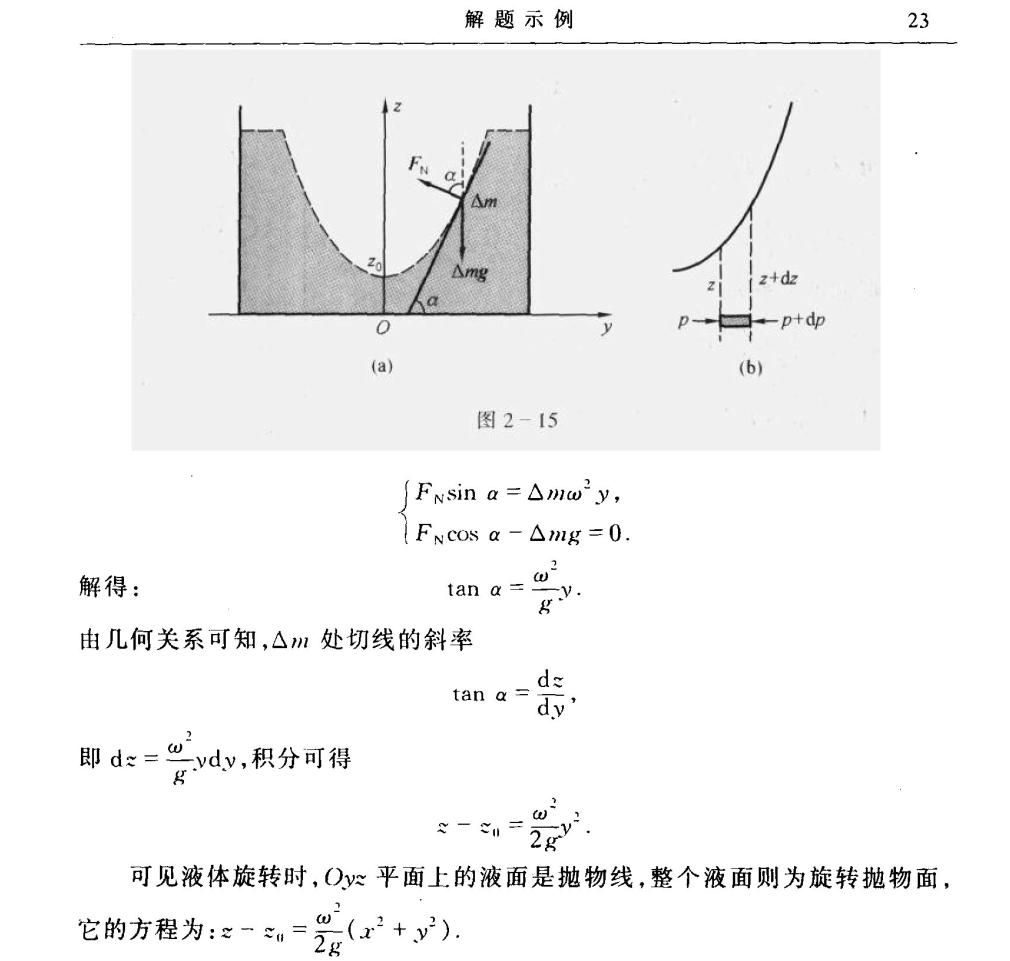
一固定光滑圆柱体上的质量为 m m m θ \theta θ
解析表达式。注意牛顿第二定律的矢量形式
N + m g = m a \boldsymbol N+m\boldsymbol g=m \boldsymbol a
N + m g = m a
{ m g sin θ = m d v d t m g cos θ − N = m v 2 R \left\{\
\begin{matrix}
mg \sin \theta = m\frac{\mathrm d v}{\mathrm d t}\\
mg \cos \theta - N= m \frac{v^2}{R}
\end{matrix}
\right.
{ m g sin θ = m d t d v m g cos θ − N = m R v 2
若使用机械能守恒定律,可以得到
1 2 m v 2 = m g ( R − R cos θ ) \frac{1}{2}mv^2=mg(R-R\cos \theta)
2 1 m v 2 = m g ( R − R cos θ )
但是,我们现在还不知道,因此,需要使用牛顿第二定律分析过程。
由于不好分析时间,根据惯用手法,我们使用:
d v d t = d v d s d s d t = d v d s v ⇒ d v d s = d v v d t = g sin θ v \frac{\mathrm d v}{\mathrm d t}=\frac{\mathrm d v}{\mathrm d s} \frac{\mathrm d s}{\mathrm d t}=\frac{\mathrm d v}{\mathrm d s} v\newline
\Rightarrow \frac{\mathrm d v}{\mathrm d s} =\frac{\mathrm d v}{v\mathrm d t}=\frac{g \sin \theta}{v}
d t d v = d s d v d t d s = d s d v v ⇒ d s d v = v d t d v = v g sin θ
这是一个微分方程,因此:
v d v = g R sin θ d θ ⇒ 1 2 v 2 = − g R cos θ + C v\mathrm d v=gR\sin \theta \mathrm d \theta \Rightarrow \frac{1}{2} v^2=-gR\cos \theta+C
v d v = g R sin θ d θ ⇒ 2 1 v 2 = − g R cos θ + C
因此
1 2 v 2 = ( − g R cos θ ) − ( − g R cos 0 ) = g ( R − R cos θ ) \frac{1}{2} v^2= (-gR \cos \theta)-(-gR\cos 0)=g(R-R\cos \theta)
2 1 v 2 = ( − g R cos θ ) − ( − g R cos 0 ) = g ( R − R cos θ )
分析小球对圆柱体的压力 N ′ N' N ′ N N N
N ′ = N = m g cos θ − m v 2 R = m g ( 3 cos θ − 2 ) N'=N=mg \cos \theta -m \frac{v^2}{R}=mg(3\cos \theta-2)
N ′ = N = m g cos θ − m R v 2 = m g ( 3 cos θ − 2 )
分析结果
质量为 n n n A B , C D A B, C D A B , C D R R R 1 / 4 1 / 4 1 / 4 B C B C B C t = 0 t=0 t = 0 v ⃗ 0 \vec{v}_0 v 0 A B A B A B μ \mu μ C D C D C D
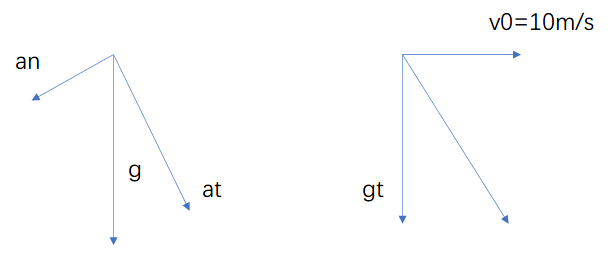
还是分析切向加速度和法向加速度。
m a n = m v 2 R = N m\boldsymbol a_n=m\frac{v^2}{R}=N
m a n = m R v 2 = N
m a t = m d v d t = − μ N = − μ m v 2 R m\boldsymbol a_t=m\frac{\mathrm d v}{\mathrm d t}=-\mu N=-\mu m \frac{v^2}{R}
m a t = m d t d v = − μ N = − μ m R v 2
可以得到 v = v ( t ) v=v(t) v = v ( t ) t t t s s s
d v d t = d v d s d s d t = d v d s v \frac{\mathrm d v}{\mathrm d t}=\frac{\mathrm d v}{\mathrm d s}\frac{\mathrm d s}{\mathrm d t}=\frac{\mathrm d v}{\mathrm d s}v
d t d v = d s d v d t d s = d s d v v
d v v = − μ R d s \frac{\mathrm d v}{v}=-\frac{\mu}{R} \mathrm d s
v d v = − R μ d s
积分得:
v = v 0 e − 1 2 π μ v=v_0 e^{-\frac{1}{2} \pi \mu}
v = v 0 e − 2 1 π μ
注意点:摩擦力符号取负号,支持力的计算。
a t = g sin θ a n = v 2 / l f ⃗ = m a x i ⃗ = m ( a t cos θ + a n sin θ ) i ⃗ = m sin θ ( g cos θ + v 2 l ) i ⃗ N ⃗ = m ( g + a y ) j ⃗ = m ( g + a n cos θ − a t sin θ ) j ⃗ \begin{aligned}
a_t & =g \sin \theta \quad a_n=v^2 / l \\
\vec{f} & =m a_x \vec{i} \\
& =m\left(a_t \cos \theta+a_n \sin \theta\right) \vec{i} \\
& =m \sin \theta\left(g \cos \theta+\frac{v^2}{l}\right) \vec{i} \\
\vec{N} & =m\left(g+a_y\right) \vec{j}=m\left(g+a_n \cos \theta-a_t \sin \theta\right) \vec{j}
\end{aligned}
a t f N = g sin θ a n = v 2 / l = m a x i = m ( a t cos θ + a n sin θ ) i = m sin θ ( g cos θ + l v 2 ) i = m ( g + a y ) j = m ( g + a n cos θ − a t sin θ ) j
作用力就要分摩擦力和支持力考虑。
由地面沿铅直方向发射质量为m的宇宙飞船。求宇宙飞船能脱离地球引力所需的最小初速度。(不计空气阻力及其它作用力,设地球半径为6378000m)
d v d t = a = − G M R 2 = d v d R v \frac{\mathrm d v}{\mathrm d t}=a=-\frac{GM}{R^2}=\frac{\mathrm d v}{\mathrm d R}v
d t d v = a = − R 2 G M = d R d v v
得到:
1 2 v 2 = G M R + C \frac{1}{2}v^2=\frac{GM}{R}+C
2 1 v 2 = R G M + C
所以最小初速度是:
2 G M R \sqrt{\frac{2GM}{R}}
R 2 G M
例: 一质量为 M M M Q \mathrm{Q} Q v 0 v_0 v 0 k ( f = − k v ) k(f=-k v) k ( f = − k v ) Q \mathrm{Q} Q P \mathrm{P} P l 0 l_0 l 0 P P P v p v_{\mathrm{p}} v p P P P F 0 F_0 F 0 F 0 F_0 F 0 α \alpha α
得到
− M k d v = d s -\frac{M}{k} \mathrm d v=\mathrm d s
− k M d v = d s
− M k v = C + s -\frac{M}{k}v=C+s
− k M v = C + s
得到 C = − M k v 0 C=-\frac{M}{k}v_0 C = − k M v 0 v p = v 0 − k l 0 M v_p=v_0-\frac{kl_0}{M} v p = v 0 − M k l 0
只用分析瞬时的问题。
切向加速度:
a t = ( F 0 cos α − k v p ) / M a_t=(F_0\cos \alpha-kv_p)/M
a t = ( F 0 cos α − k v p ) / M
法向加速度:
a n = F 0 sin α / M a_n=F_0 \sin \alpha/M
a n = F 0 sin α / M
而曲率半径:
ρ = v p 2 a n = M v p 2 F 0 sin α \rho=\frac{v_p^2}{a_n}=\frac{Mv_p^2}{F_0 \sin\alpha}
ρ = a n v p 2 = F 0 sin α M v p 2
v p v_p v p
摩擦的临界角问题:
F f = m g sin θ F N = m g cos θ μ s ≥ F f / F N = tan θ F_f=mg\sin\theta\\
F_N=mg\cos\theta\\
\mu_s \ge F_f/F_N=\tan\theta
F f = m g sin θ F N = m g cos θ μ s ≥ F f / F N = tan θ
近地重力加速度的近似:
g ′ = G M ( R + h ) 2 g'=\frac{GM}{(R+h)^2}
g ′ = ( R + h ) 2 G M
( 1 + h R ) − 2 ≈ 1 − 2 h R (1+\frac{h}{R})^{-2} \approx 1-2\frac{h}{R}
( 1 + R h ) − 2 ≈ 1 − 2 R h
因此:
g ≈ g 0 ( 1 − 2 h R ) g \approx g_0(1-2\frac{h}{R})
g ≈ g 0 ( 1 − 2 R h )
**质量为 m m m F 0 F_0 F 0 v v v v 0 v_0 v 0 l l l 4 l / 5 4l/5 4 l / 5
极限速度:受力平衡。设比例系数为 k k k f = − k v f=-kv f = − k v
F 0 + f = F 0 − k v 0 = 0 ⇒ k = F 0 v 0 F_0+f=F_0-kv_0=0 \Rightarrow k=\frac{F_0}{v_0}
F 0 + f = F 0 − k v 0 = 0 ⇒ k = v 0 F 0
关闭发动机后
m a = m d v d t = − k v ma=m\frac{\mathrm d v}{\mathrm d t}=-kv
m a = m d t d v = − k v
事实上,这类条件等价于 d v / d s = − k / m \mathrm d v/\mathrm d s=-k/m d v / d s = − k / m
0 = − k l / m + v 0 ⇒ l = m v 0 k = m v 0 2 F 0 0=-kl/m+v_0 \Rightarrow l=\frac{mv_0}{k}=\frac{mv_0^2}{F_0}
0 = − k l / m + v 0 ⇒ l = k m v 0 = F 0 m v 0 2
v ′ = 1 5 v 0 v'=\frac{1}{5}v_0
v ′ = 5 1 v 0
实际上反映了速度和路程正相关。
∫ t = 0 t 0 d v d t d t = − 4 5 v 0 \int_{t=0}^{t_0} \frac{\mathrm d v}{\mathrm d t}\mathrm d t=-\frac{4}{5} v_0
∫ t = 0 t 0 d t d v d t = − 5 4 v 0
为了求出速度,需要变换微分方程 a = − k v / m a=-kv/m a = − k v / m
t = − m ln v / k + C ′ ⇒ C ′ = m ln v 0 / k ⇒ t 0 = m / k ( ln v 0 − ln ( 1 / 5 v 0 ) ) = m v 0 F 0 ln 5 t=-m\ln v/k+C' \Rightarrow C'=m\ln v_0/k\\\Rightarrow t_0=m/k(\ln v_0-\ln (1/5v_0))=\frac{m v_0}{F_0}\ln 5
t = − m ln v / k + C ′ ⇒ C ′ = m ln v 0 / k ⇒ t 0 = m / k ( ln v 0 − ln ( 1 / 5 v 0 ) ) = F 0 m v 0 ln 5
绳绕圆柱问题
( F T + d F T ) cos d θ 2 − F T cos d θ 2 − F f = 0 , F f = μ F N − ( F T + d F T ) sin d θ 2 − F T sin d θ 2 + F N = 0 (F_T+\mathrm d F_T) \cos \frac{\mathrm d \theta}{2}-F_T\cos \frac{\mathrm d \theta}{2} -F_f=0,F_f=\mu F_N\\
-(F_T+\mathrm d F_T)\sin \frac{\mathrm d \theta}{2}-F_T\sin \frac{\mathrm d \theta}{2}+F_N=0
( F T + d F T ) cos 2 d θ − F T cos 2 d θ − F f = 0 , F f = μ F N − ( F T + d F T ) sin 2 d θ − F T sin 2 d θ + F N = 0
近似 $\sin,\cos $,
也可以直接做力的分解:
N = 2 F T ⋅ d θ 2 = F T d θ d θ = μ N N=2F_T\cdot \frac{\mathrm d \theta}{2}=F_T \mathrm d \theta \quad \mathrm d \theta=\mu N
N = 2 F T ⋅ 2 d θ = F T d θ d θ = μ N
∫ F T B F T A d F T F T = μ ∫ 0 θ d θ \int_{F_{T_B}}^{F_{T_A}}\frac{\mathrm d F_T}{F_T}=\mu\int_0^\theta \mathrm d \theta
∫ F T B F T A F T d F T = μ ∫ 0 θ d θ
F T B F T A = e − μ θ \frac{F_{T_B}}{F_{T_A}}=e^{-\mu \theta}
F T A F T B = e − μ θ
如图所示,飞机以水平速度 v 0 v_0 v 0 x = l x=l x = l y = h y=h y = h m m m v 0 v_0 v 0
确定飞机的轨道方程:y = h l 2 x 2 y=\frac{h}{l^2} x^2 y = l 2 h x 2 y y y a ( x ) a(x) a ( x )
tan ( θ ( x ) ) = 2 h l 2 a t ( x ) = a ( x ) cos ( θ ( x ) ) a n ( x ) = a ( x ) sin ( θ ( x ) ) = v ( x ) 2 ρ ( x ) \tan(\theta(x))=\frac{2h}{l^2}\\
a_t(x)=a(x) \cos (\theta (x))\\
a_n(x)=a(x) \sin (\theta (x))=\frac{v(x)^2}{\rho(x)}
tan ( θ ( x ) ) = l 2 2 h a t ( x ) = a ( x ) cos ( θ ( x ) ) a n ( x ) = a ( x ) sin ( θ ( x ) ) = ρ ( x ) v ( x ) 2
而 ρ ( x ) = \rho(x)= ρ ( x ) =
几何关系的约束,转化为参数方程:
d y d t = 2 k x d x d t v y = 2 k v 0 x a y = v y ′ = 2 h v 0 2 l 2 \frac{\mathrm d y}{\mathrm d t}=2kx \frac{\mathrm d x}{\mathrm d t}\\
v_y=2kv_0x\\
a_y=v_y'=\frac{2hv_0^2}{l^2}
d t d y = 2 k x d t d x v y = 2 k v 0 x a y = v y ′ = l 2 2 h v 0 2
得到:
F s = m g + m a y = m ( 2 h v 0 2 l 2 + g ) F_s=mg+ma_y=m\left(\frac{2hv_0^2}{l^2}+g\right)
F s = m g + m a y = m ( l 2 2 h v 0 2 + g )
注意飞机的重力。
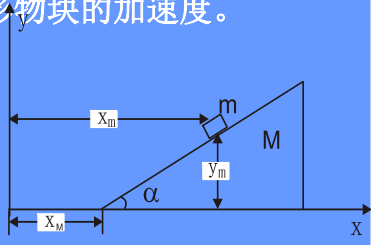
一质量为 M M M α \alpha α m m m
设各面之间的摩擦力均可忽略不计。试按照下列三种方法求解三角形物块的加速度。
用牛顿定律及约束方程。
由几何约束关系:
y m = ( x m − x M ) tan α y_m=(x_m-x_M)\tan \alpha
y m = ( x m − x M ) tan α
a m y = ( a m x − a M x ) tan α a_{my}=(a_{mx}-a_{Mx})\tan \alpha
a m y = ( a m x − a M x ) tan α
加速度正方向为 距离减小 的方向。
做受力分析:
M a M x = − N sin α m a m x = N sin α m a m y = m g − N cos α Ma_{Mx}=-N\sin \alpha\\
ma_{mx}=N \sin \alpha\\
ma_{my}=mg-N\cos \alpha
M a M x = − N sin α m a m x = N sin α m a m y = m g − N cos α
得到
N = g m M cos α M + m sin 2 α N=\frac{gmM\cos\alpha }{M+m\sin^2\alpha}
N = M + m sin 2 α g m M cos α
题目要求 a M x a_{Mx} a M x
a M x = − N sin α M = − m g sin α cos α M + m sin 2 α a_{Mx}=-\frac{N\sin\alpha}{M}=-\frac{mg\sin\alpha\cos \alpha}{M+m\sin^2\alpha}
a M x = − M N sin α = − M + m sin 2 α m g sin α cos α
朝向 x x x
结果分析:
当 α → π 2 \alpha \to \frac{\pi}{2} α → 2 π α → 0 \alpha \to 0 α → 0 → 0 \to 0 → 0
用牛顿定律及 运动叠加 原理。
分析小滑块的运动,由于小滑块只能在斜面上运动,因此会有朝向斜面的加速度分量 a m \boldsymbol a_m a m a M \boldsymbol a_M a M a m + a M \boldsymbol a_m+\boldsymbol a_M a m + a M
对于三角块。
N sin α = M a M N\sin\alpha=Ma_M
N sin α = M a M
对于小滑块:N − m g cos α N-mg \cos \alpha N − m g cos α a m + a M \boldsymbol a_m+\boldsymbol a_M a m + a M N N N m g sin α mg \sin \alpha m g sin α a m + a M \boldsymbol a_m+\boldsymbol a_M a m + a M N N N
N − m g cos α = a M cos α m g sin α = a M cos α − a m N-mg \cos \alpha=a_M\cos \alpha\\
mg \sin \alpha=a_M \cos \alpha-a_m
N − m g cos α = a M cos α m g sin α = a M cos α − a m
解得:
a M = m g sin α cos α M + m sin 2 α a_M=\frac{mg\sin\alpha\cos \alpha}{M+m\sin^2\alpha}
a M = M + m sin 2 α m g sin α cos α
用非惯性系中力学定律,需要引入惯性力。
设斜面的加速度为 a M a_M a M m a M m a_M m a M
N sin α = M a M N + m a M sin α = m g cos α N\sin \alpha=M a_M\\
N+ma_M\sin\alpha=mg\cos \alpha
N sin α = M a M N + m a M sin α = m g cos α
得到
N = m M g cos α M + m sin 2 α N=\frac{mMg\cos \alpha}{M+m\sin^2\alpha}
N = M + m sin 2 α m M g cos α
因此 a M = m g sin α cos α M + m sin 2 α a_M=\frac{mg\sin\alpha\cos \alpha}{M+m\sin^2\alpha} a M = M + m sin 2 α m g sin α cos α
关联加速度问题
设 m 1 m_1 m 1 a 1 a_1 a 1 m 1 m_1 m 1 m 3 m_3 m 3 a 2 a_2 a 2
绳拉力为 T T T m 3 m_3 m 3 m 1 m_1 m 1 N N N
因此对 m 1 m_1 m 1
N + T − F = m a 1 N+T-F=ma_1
N + T − F = m a 1
对 m 3 m_3 m 3
N = m a 1 m a 2 = T − m g N=ma_1\\
ma_2=T-mg
N = m a 1 m a 2 = T − m g
对 m 2 m_2 m 2
m a 1 − T = m a 2 ma_1-T=ma_2
m a 1 − T = m a 2
等效重力
阻力问题
− m g − k v = m d v d t \boxed{-mg-kv=m \frac{\mathrm d v}{\mathrm d t}}
− m g − k v = m d t d v
是阻力,所以带负号。
得到:
d v m g + k v = − 1 m d t \frac{\mathrm d v}{mg+kv}=-\frac{1}{m} \mathrm d t
m g + k v d v = − m 1 d t
ln ( m g + k v m g + k v 0 ) = − k m t \ln\left(\frac{mg+kv}{mg+kv_0}\right)=-\frac{k}{m}t
ln ( m g + k v 0 m g + k v ) = − m k t
这里直接给出了常数项。
解运动规律还需要知道任意时间的位移和加速度。
y = ∫ 0 t v d t a = d v d t y=\int_0^t v\mathrm d t \qquad
a=\frac{\mathrm d v}{\mathrm d t}
y = ∫ 0 t v d t a = d t d v
求解最高点?此时 v = 0 v=0 v = 0 t 0 t_0 t 0 y y y d v d t = v d v d y \frac{dv}{dt}=v\frac{dv}{dy} d t d v = v d y d v
讨论是必要的,可以代入特殊情况看算的合不合理。
当转速为 ω \omega ω 3 m g \sqrt{3}mg 3 m g 2 ω 2\omega 2 ω 4 3 m g 4\sqrt{3}mg 4 3 m g
( T 1 − T 2 ) sin 30 ° = m g ( T 1 + T 2 ) cos 30 ° = 4 3 m g (T_1-T_2) \sin 30 \degree=mg\\
(T_1+T_2) \cos 30 \degree=4\sqrt{3}mg
( T 1 − T 2 ) sin 3 0 ° = m g ( T 1 + T 2 ) cos 3 0 ° = 4 3 m g
即可得到 T 1 = 5 m g , T 2 = 3 m g T_1=5mg,T_2=3mg T 1 = 5 m g , T 2 = 3 m g
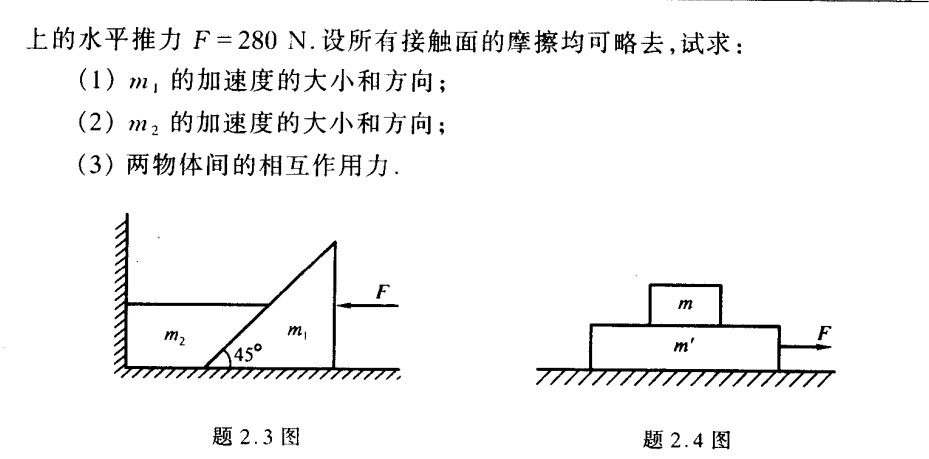
m 2 m_2 m 2 m 1 m_1 m 1
F − 2 2 N 2 = m 1 a 1 F-\frac{\sqrt{2}}{2}N_2=m_1a_1\\
F − 2 2 N 2 = m 1 a 1
2 2 N 2 − m 2 g = m 2 a 2 \frac{\sqrt{2}}{2}N_2-m_2g=m_2a_2
2 2 N 2 − m 2 g = m 2 a 2
现在只有这两个方程,不过两者加速度有关联。不妨取 m 2 m_2 m 2
a 1 = a 2 a_1=a_2
a 1 = a 2
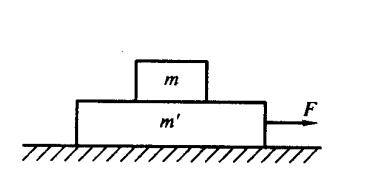
物体与板之间的作用力:f = m a , N = m g f=ma,N=mg f = m a , N = m g
板与桌面间的相互作用力:f ′ = F − ( m + m ′ ) a = μ k ( m + m ′ ) g , N ′ = ( m + m ′ ) g f'=F-(m+m')a=\mu_k(m+m')g,N'=(m+m')g f ′ = F − ( m + m ′ ) a = μ k ( m + m ′ ) g , N ′ = ( m + m ′ ) g
板从物体下面抽出:a = μ s g a=\mu_sg a = μ s g F = ( μ k + μ s ) ( m + m ′ ) g F=(\mu_k+\mu_s)(m+m')g F = ( μ k + μ s ) ( m + m ′ ) g
“下滑力”:
F = m g sin θ − μ m g cos θ = ( 2.4 − 3.2 μ ) g N F=mg\sin \theta-\mu mg \cos \theta=(2.4-3.2\mu)g ~ \mathrm{N}
F = m g sin θ − μ m g cos θ = ( 2 . 4 − 3 . 2 μ ) g N
运动方程:
m d v d t = F − k v m\frac{\mathrm d v}{\mathrm d t}=F-kv
m d t d v = F − k v
得到:
ln ( F − k v F − k v 0 ) = − k t m \ln\left(\frac{F-kv}{F-kv_0}\right)=-\frac{kt}{m}
ln ( F − k v 0 F − k v ) = − m k t
趋近于 10 m / s 10 \mathrm{~m/s} 1 0 m / s F − 10 k = 0 F-10k=0 F − 1 0 k = 0
切线斜率:g / 4 g/4 g / 4 m g / 4 = F − 5 k mg/4=F-5k m g / 4 = F − 5 k
k = 1.96 k g / s μ = 0.125 k=1.96 \mathrm{~kg/s}\\
\mu=0.125
k = 1 . 9 6 k g / s μ = 0 . 1 2 5
r = R cos q B m t i + R sin q B m t j + c t k \boldsymbol r=R\cos \frac{qB}{m}t \boldsymbol i +R\sin \frac{qB}{m}t \boldsymbol j + ct \boldsymbol k
r = R cos m q B t i + R sin m q B t j + c t k
v = − q B R m sin q B m t i + q B R m cos q B m t j + c k \boldsymbol v=-\frac{qBR}{m}\sin \frac{qB}{m}t \boldsymbol i +\frac{qBR}{m}\cos \frac{qB}{m}t \boldsymbol j + c \boldsymbol k
v = − m q B R sin m q B t i + m q B R cos m q B t j + c k
a = − q 2 B 2 R m 2 cos q B m t i − q 2 B 2 R m 2 sin q B m t j \boldsymbol a=-\frac{q^2B^2R}{m^2}\cos \frac{qB}{m}t \boldsymbol i -\frac{q^2B^2R}{m^2}\sin \frac{qB}{m}t \boldsymbol j
a = − m 2 q 2 B 2 R cos m q B t i − m 2 q 2 B 2 R sin m q B t j
∣ a ∣ = q 2 B 2 R m 2 |\boldsymbol a|=\frac{q^2B^2R}{m^2}
∣ a ∣ = m 2 q 2 B 2 R
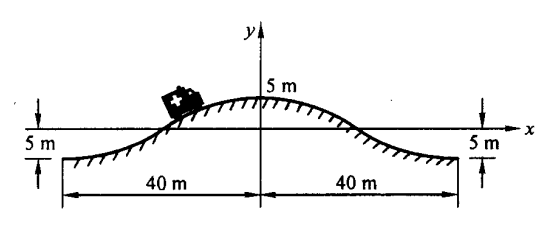
设余弦曲线为 A cos ω x A\cos \omega x A cos ω x
ρ = ∣ ( 1 + y ′ 2 ) 3 2 y ′ ′ ∣ = ∣ 1 − A ω 2 cos ω ⋅ 0 ∣ = 1 A ω 2 \rho=\boxed{\left | \frac{(1+y'^2)^\frac{3}{2}}{y''}\right |}=\left|\frac{1}{-A\omega^2\cos\omega \cdot0}\right|=\frac{1}{A\omega^2}
ρ = ∣ ∣ ∣ ∣ ∣ y ′ ′ ( 1 + y ′ 2 ) 2 3 ∣ ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ − A ω 2 cos ω ⋅ 0 1 ∣ ∣ ∣ ∣ = A ω 2 1
代入 A = 5 m , ω = 1 40 π m − 1 A=5 \mathrm{~m},\omega=\frac{1}{40}\pi \mathrm{~m^{-1}} A = 5 m , ω = 4 0 1 π m − 1
ρ = 320 π 2 \rho=\frac{320}{\pi^2}
ρ = π 2 3 2 0
因此加速度为
a n = v 2 ρ a_n=\frac{v^2}{\rho}
a n = ρ v 2
压力为:
N = m g − m a n = 2.15 × 1 0 4 N N=mg-ma_n=2.15 \times 10^{4} \mathrm{~N}
N = m g − m a n = 2 . 1 5 × 1 0 4 N
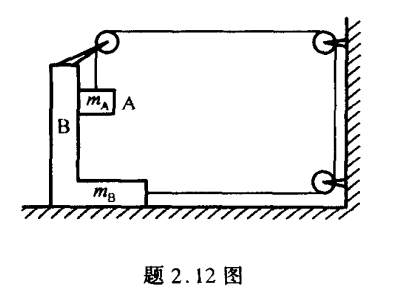
使用运动的叠加原理,设 B B B a 1 a_1 a 1 A A A a 2 a_2 a 2
而且,有几何的约束关系。B B B l l l 2 l 2l 2 l A A A 2 l 2l 2 l
因此,不妨设 a 1 = a , a 2 = 2 a a_1=a,a_2=2a a 1 = a , a 2 = 2 a
对于 m A m_A m A
2 m A a = m A g − T m A a = N 2m_Aa=m_Ag-T\\
m_Aa=N
2 m A a = m A g − T m A a = N
对于 m B m_B m B
2 T − N = m B a 2T-N=m_Ba
2 T − N = m B a
注意绳子对滑轮的力 。
得到
N = 2 m A 5 m A + m B m A g N=\frac{2m_A}{5m_A+m_B}m_Ag
N = 5 m A + m B 2 m A m A g
因此:
a = 2 m A g 5 m A + m B a=\frac{2m_Ag}{5m_A+m_B}
a = 5 m A + m B 2 m A g
得到:
a B = 2 m A g 5 m A + m B i a A = 2 m A g 5 m A + m B i − 4 m A g 5 m A + m B j \boldsymbol a_B=\frac{2m_Ag}{5m_A+m_B}\boldsymbol i\\
\boldsymbol a_A=\frac{2m_Ag}{5m_A+m_B}\boldsymbol i-\frac{4m_Ag}{5m_A+m_B}\boldsymbol j
a B = 5 m A + m B 2 m A g i a A = 5 m A + m B 2 m A g i − 5 m A + m B 4 m A g j
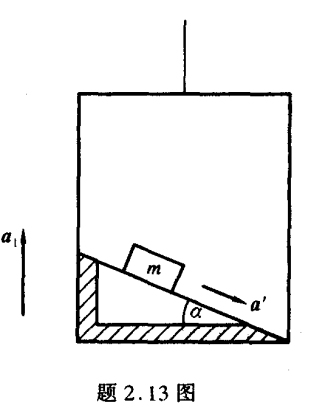
等效重力加速度:( g + a 1 ) (g+a_1) ( g + a 1 )
物体相对于斜面的加速度:
a ′ = ( g + a 1 ) sin α cos α i − ( g + a 1 ) sin 2 α j \boldsymbol a'=(g+a_1)\sin\alpha\cos \alpha \boldsymbol i-(g+a_1)\sin^2\alpha\boldsymbol j
a ′ = ( g + a 1 ) sin α cos α i − ( g + a 1 ) sin 2 α j
从地面上看:
a = a ′ + a 1 = a ′ = ( g + a 1 ) sin α cos α i + ( a 1 − ( g + a 1 ) sin 2 α ) j \boldsymbol a=\boldsymbol a'+\boldsymbol a_1=\boldsymbol a'=(g+a_1)\sin\alpha\cos \alpha \boldsymbol i+(a_1-(g+a_1)\sin^2\alpha)\boldsymbol j
a = a ′ + a 1 = a ′ = ( g + a 1 ) sin α cos α i + ( a 1 − ( g + a 1 ) sin 2 α ) j
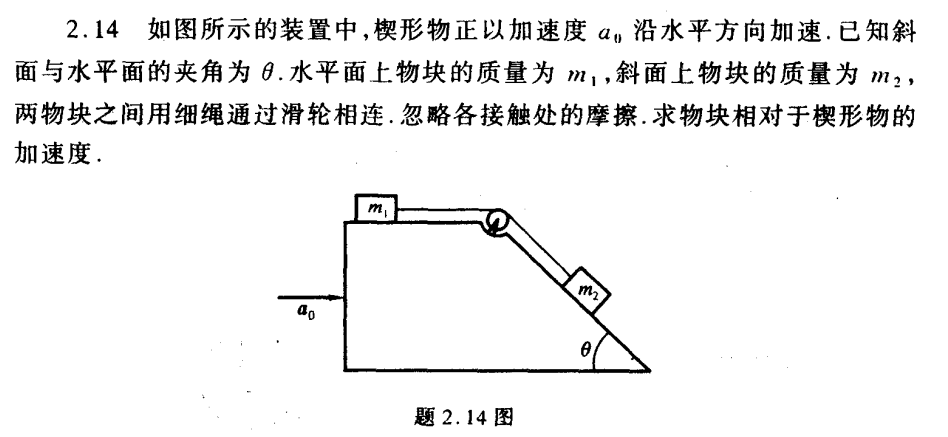
以楔形物为参照系,需要受水平朝左的惯性力。
m 1 a = m 1 a 0 − T T + m 2 a 0 cos θ − m 2 g sin θ = m 2 a m_1a=m_1a_0-T\\
T+m_2a_0\cos \theta-m_2g\sin\theta=m_2a
m 1 a = m 1 a 0 − T T + m 2 a 0 cos θ − m 2 g sin θ = m 2 a
得到
a = m 2 a 0 cos θ − m 2 g sin θ + m 1 a 0 m 1 + m 2 a=\frac{m_2a_0\cos \theta-m_2g\sin\theta+m_1a_0}{m_1+m_2}
a = m 1 + m 2 m 2 a 0 cos θ − m 2 g sin θ + m 1 a 0
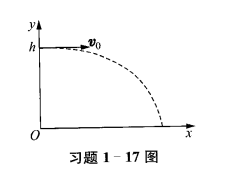
如题图所示,一质量为 m m m h h h v 0 v_0 v 0 v 0 v_0 v 0
小球的运动方程。2. 小球在落地之前的轨迹方程。
{ x = v 0 t y = h − 1 2 g t 2 \left\{
\begin{matrix}
x=v_0t\\
y=h-\frac{1}{2}gt^2
\end{matrix}
\right.
{ x = v 0 t y = h − 2 1 g t 2
因此,运动方程为:
r = v 0 t i + ( h − 1 2 g t 2 ) j \boldsymbol r=v_0t\boldsymbol i+(h-\frac{1}{2}gt^2)\boldsymbol j
r = v 0 t i + ( h − 2 1 g t 2 ) j
得到 t = x / v 0 t=x/v_0 t = x / v 0
y = h − g x 2 2 v 0 2 y=h-\frac{gx^2}{2v_0^2}
y = h − 2 v 0 2 g x 2
落地前瞬时小球的
d r d t = v 0 i − g t j \frac{\mathrm d \boldsymbol r}{\mathrm d t}=v_0\boldsymbol i-gt\boldsymbol j
d t d r = v 0 i − g t j
d v d t = − g j \frac{\mathrm d \boldsymbol v}{\mathrm d t}=-g \boldsymbol j
d t d v = − g j
v = v 0 2 + g 2 t 2 , d v d t = g 2 t v 0 2 + g 2 t 2 v=\sqrt{v_0^2+g^2t^2},\frac{\mathrm d v}{\mathrm d t}=\frac{g^2t}{\sqrt{v_0^2+g^2t^2}}
v = v 0 2 + g 2 t 2 , d t d v = v 0 2 + g 2 t 2 g 2 t
代入 t = 2 h / g t=\sqrt{2h/g} t = 2 h / g
d r d t = v 0 i − 2 g h j \frac{\mathrm d \boldsymbol r}{\mathrm d t}=v_0\boldsymbol i-\sqrt{2gh}\boldsymbol j
d t d r = v 0 i − 2 g h j
d v d t = − g j \frac{\mathrm d \boldsymbol v}{\mathrm d t}=-g \boldsymbol j
d t d v = − g j
d v d t = g 2 g h v 0 2 + 2 g h \frac{\mathrm d v}{\mathrm d t}=\frac{g\sqrt{2gh}}{\sqrt{v_0^2+2gh}}
d t d v = v 0 2 + 2 g h g 2 g h
小球以 10 m / s 10 \mathrm{~m/s} 1 0 m / s 5 m / s 2 5 \mathrm{~m/s^2} 5 m / s 2
加速度与速度方向的夹角 θ = arctan ( v 0 g t ) \theta=\arctan (\frac{v_0}{gt}) θ = arctan ( g t v 0 ) v 0 v_0 v 0 10 m / s 10 \mathrm{~m/s} 1 0 m / s
法向加速度 a n = g sin θ = 5 m / s 2 a_n=g\sin \theta=5 \mathrm{~m/s^2} a n = g sin θ = 5 m / s 2 θ = π / 6 \theta=\pi/6 θ = π / 6 t = 3 v 0 g t=\sqrt{3}\frac{v_0}{g} t = 3 g v 0 h = 1 / 2 g t 2 = 3 v 0 2 / 2 g = 15 m h=1/2gt^2=3v_0^2/2g=15 \mathrm{~m} h = 1 / 2 g t 2 = 3 v 0 2 / 2 g = 1 5 m a n = v 2 ρ a_n=\frac{v^2}{\rho} a n = ρ v 2 ρ = v 2 a n \rho=\frac{v^2}{a_n} ρ = a n v 2 v 2 = v 0 2 + g 2 t 2 = 400 m 2 / s 2 v^2=v_0^2+g^2t^2=400 \mathrm{~m^2/s^2} v 2 = v 0 2 + g 2 t 2 = 4 0 0 m 2 / s 2 ρ = 80 m \rho=80\mathrm{~m} ρ = 8 0 m
一质点做半径为 R R R t = 0 t=0 t = 0 P P P v = A + B t v=A+Bt v = A + B t A , B A,B A , B P P P
运动一周的时间
s ( t ) = ∫ v d t = A t + 1 2 B t 2 ⇒ s ( t 0 ) − s ( 0 ) = 2 π R , t 0 = − A + A 2 + 4 π R B B s(t)=\int v\mathrm d t=At+\frac{1}{2}Bt^2 \\
\Rightarrow s(t_0)-s(0)=2\pi R,t_0=\frac{-A+\sqrt{A^2+4\pi RB}}{B}
s ( t ) = ∫ v d t = A t + 2 1 B t 2 ⇒ s ( t 0 ) − s ( 0 ) = 2 π R , t 0 = B − A + A 2 + 4 π R B
运动一周的加速度
a t = d v d t = B a n = v t 0 2 R = ( A + B t 0 ) 2 R = A 2 R + 4 π B a_t=\frac{\mathrm d v}{\mathrm d t}=B\\
a_n=\frac{v_{t_0}^2}{R}=\frac{(A+Bt_0)^2}{R}=\frac{A^2}{R}+4\pi B
a t = d t d v = B a n = R v t 0 2 = R ( A + B t 0 ) 2 = R A 2 + 4 π B
一小船相对于河水以速度 v v v u u u
以河水为参考系,发觉时船行距离 2 v 2v 2 v 2 s 2\mathrm{~s} 2 s
如题图所示,a b c abc a b c y = H − K x 2 y=H-Kx^2 y = H − K x 2 m m m x x x v x = V v_x=V v x = V x 0 x_0 x 0

速度矢量和加速度矢量。
v y v x = k = d y d x = − 2 K x \frac{v_y}{v_x}=k=\frac{\mathrm d y}{\mathrm d x}=-2Kx
v x v y = k = d x d y = − 2 K x
v = V i − 2 K V x 0 j \boldsymbol v=V\boldsymbol i-2KVx_0\boldsymbol j
v = V i − 2 K V x 0 j
加速度矢量:
a = d v d t = − 2 K V d x 0 d t j = − 2 K V 2 j \boldsymbol a=\frac{\mathrm d \boldsymbol v}{\mathrm d t}=-2KV\frac{\mathrm d x_0}{\mathrm d t} \boldsymbol j=-2KV^2 \boldsymbol j
a = d t d v = − 2 K V d t d x 0 j = − 2 K V 2 j
还有一种方法:tan θ = y ′ = − 2 K x \tan \theta = y'=-2Kx tan θ = y ′ = − 2 K x v y = v x tan θ v_y=v_x \tan \theta v y = v x tan θ
切向加速度与法向加速度。
a t = − ∣ a ∣ sin θ = 4 K x 0 ( 2 K x 0 ) 2 + 1 K V 2 a n = ∣ a ∣ cos θ = 2 ( 2 K x 0 ) 2 + 1 K V 2 a_t=-|\boldsymbol a|\sin \theta=\frac{4Kx_0}{\sqrt{(2Kx_0)^2+1}}KV^2\\
a_n=|\boldsymbol a|\cos \theta=\frac{2}{\sqrt{(2Kx_0)^2+1}}KV^2
a t = − ∣ a ∣ sin θ = ( 2 K x 0 ) 2 + 1 4 K x 0 K V 2 a n = ∣ a ∣ cos θ = ( 2 K x 0 ) 2 + 1 2 K V 2
也可以使用 v = V 2 + ( 2 K V x ) 2 v=\sqrt{V^2+(2KVx)^2} v = V 2 + ( 2 K V x ) 2
a t = d v d x ⋅ d x d t = 4 K 2 V 2 x V 2 + ( 2 K V x ) 2 ⋅ V a_t=\frac{\mathrm d v}{\mathrm d x}\cdot \frac{\mathrm d x}{\mathrm d t}=\frac{4K^2V^2x}{\sqrt{V^2+(2KVx)^2}}\cdot V
a t = d x d v ⋅ d t d x = V 2 + ( 2 K V x ) 2 4 K 2 V 2 x ⋅ V
利用 a 2 = a t 2 + a n 2 a^2=a_t^2+a_n^2 a 2 = a t 2 + a n 2 a n a_n a n
注意:对谁求导。

斜面的问题
一足够大的斜面倾角为 θ \theta θ μ = tan θ \mu=\tan \theta μ = tan θ v 0 v_0 v 0
以沿斜面向下为 j \boldsymbol j j i \boldsymbol i i
v x 0 = v 0 i \boldsymbol v_{x0}=v_0\boldsymbol i v x 0 = v 0 i v y 0 = 0 \boldsymbol v_{y0}=0 v y 0 = 0
α = arctan v y v x F x = − μ m g cos θ cos α F y = m g sin θ − μ m g cos θ sin α d v x d t = F x / m d v y d t = F y / m \alpha=\arctan \frac{v_y}{v_x}\\
F_x=-\mu mg \cos \theta \cos \alpha\\
F_y=mg\sin \theta-\mu mg \cos \theta \sin \alpha \\
\frac{\mathrm d v_x}{\mathrm d t}=F_x/m\quad \frac{\mathrm d v_y}{\mathrm d t}=F_y/m
α = arctan v x v y F x = − μ m g cos θ cos α F y = m g sin θ − μ m g cos θ sin α d t d v x = F x / m d t d v y = F y / m
到最后,物块速度应该趋于稳定,即
F x = 0 F y = 0 F_x=0 \quad F_y=0
F x = 0 F y = 0
推出 cos α = 0 \cos \alpha = 0 cos α = 0 v x → 0 v_x \to 0 v x → 0
考虑到
f 阻 = c 1 v 2 + μ ( m g − c 2 v 2 ) m g = c 2 v 0 2 f_{阻}=c_1v^2+\mu(mg-c_2v^2) \quad mg=c_2v_0^2
f 阻 = c 1 v 2 + μ ( m g − c 2 v 2 ) m g = c 2 v 0 2
得到
− m d v d t = c 1 v 2 + μ ( c 2 v 0 2 − c 2 v 2 ) -m\frac{\mathrm d v}{\mathrm d t}=c_1v^2+\mu(c_2v_0^2-c_2v^2)
− m d t d v = c 1 v 2 + μ ( c 2 v 0 2 − c 2 v 2 )
考虑到需要求滑行距离,因此需要变换
− m v d v d x = c 1 v 2 + μ ( c 2 v 0 2 − c 2 v 2 ) -mv\frac{\mathrm d v}{\mathrm d x}=c_1v^2+\mu(c_2v_0^2-c_2v^2)
− m v d x d v = c 1 v 2 + μ ( c 2 v 0 2 − c 2 v 2 )
得到:
d x = − m v d v μ c 2 v 0 2 + ( c 1 − μ c 2 ) v 2 ∫ 0 x c d x = − ∫ v 0 0 m v d v μ m g + ( c 1 − μ c 2 ) v 2 x c = 1 2 ln ( μ m g + ( c 1 − μ c 2 ) v 0 2 / μ m g ) × m c 1 − μ c 2 \mathrm d x=\frac{-mv\mathrm d v}{\mu c_2v_0^2+(c_1-\mu c_2)v^2}\\
\int_0^{x_c} \mathrm d x=-\int_{v_0}^0 \frac{mv\mathrm d v}{\mu mg+(c_1-\mu c_2)v^2}\\
x_c=\frac{1}{2} \ln (\mu mg+(c_1-\mu c_2)v_0^2/\mu mg) \times \frac{m}{c_1-\mu c_2}
d x = μ c 2 v 0 2 + ( c 1 − μ c 2 ) v 2 − m v d v ∫ 0 x c d x = − ∫ v 0 0 μ m g + ( c 1 − μ c 2 ) v 2 m v d v x c = 2 1 ln ( μ m g + ( c 1 − μ c 2 ) v 0 2 / μ m g ) × c 1 − μ c 2 m
x c = c 2 v 0 2 2 g ( c 1 − μ c 2 ) ln ( c 1 v 0 2 μ c 2 v 0 2 ) x_c=\frac{c_2 v_0^2}{2g(c_1-\mu c_2)}\ln \left(\frac{c_1v_0^2}{\mu c_2 {v_0^2}}\right)
x c = 2 g ( c 1 − μ c 2 ) c 2 v 0 2 ln ( μ c 2 v 0 2 c 1 v 0 2 )


和绕的长度没有关系。


隔离B,在水平方向应用牛二,有:
N sin θ − μ ( m B g + N cos θ ) = m B a > 0 N\sin \theta-\mu(m_Bg+N\cos \theta)=m_Ba >0
N sin θ − μ ( m B g + N cos θ ) = m B a > 0
隔离A,在两个方向上:
N cos θ ≤ m A g N\cos \theta \le m_Ag
N cos θ ≤ m A g
因此:
m A g cos θ ≥ N > μ m B g sin θ − μ cos θ \frac{m_Ag}{\cos \theta} \ge N > \frac{\mu m_Bg}{\sin\theta -\mu\cos\theta}
cos θ m A g ≥ N > sin θ − μ cos θ μ m B g
因此,为了保证不等号成立:
μ < m A m A + m B tan θ \mu < \frac{m_A}{m_A+m_B} \tan\theta
μ < m A + m B m A tan θ
当 μ \mu μ m A g − N cos θ m_A g -N\cos \theta m A g − N cos θ A A A μ ( m A g − N cos θ ) \mu(m_A g -N\cos \theta) μ ( m A g − N cos θ ) A A A
F − μ ( m A g − N cos θ ) − N sin θ = m A a F-\mu(m_A g -N\cos \theta)-N\sin\theta=m_A a
F − μ ( m A g − N cos θ ) − N sin θ = m A a
得到
F = N ( sin θ − μ cos θ ) ( 1 + m A m B ) F=N(\sin\theta -\mu\cos \theta)(1+\frac{m_A}{m_B})
F = N ( sin θ − μ cos θ ) ( 1 + m B m A )
将 N N N