P4727 [HNOI2009]图的同构计数

这种题的核心在于手玩和检验。

按照常规套路，对于一个置换，我们将其分割为若干个循环置换，求算有多少加边的方案使得其经过置换后仍然同构，即置换后的边 $(p_i,p_j)$ 相连当且仅当原边 $(i,j)$ 相连。

这样，我们就有两个讨论方向：

$i,j$ 同属于一个循环置换之内。
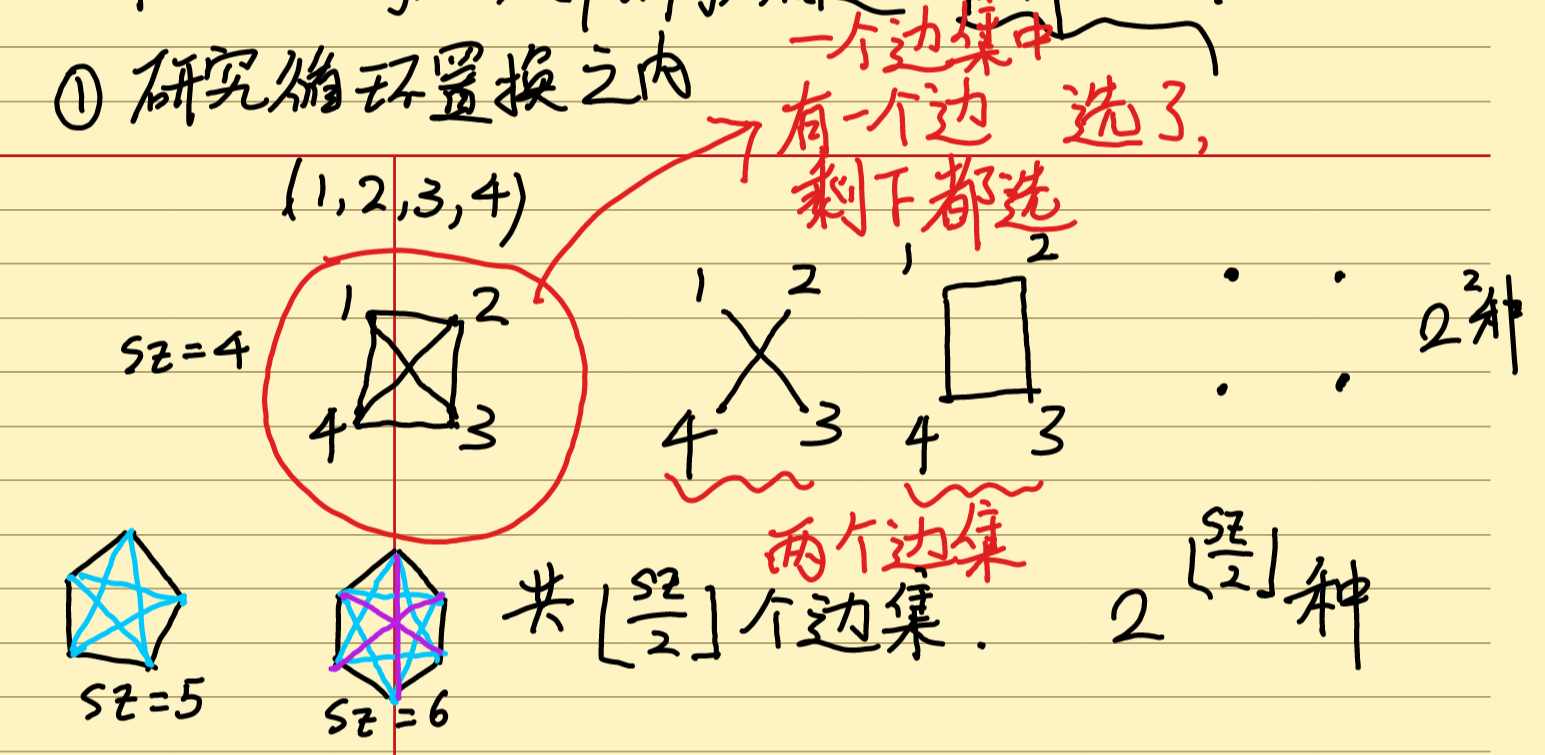
$i,j$ 属于两个循环置换。

于是答案就是：

pow(2,\sum_{i} [\frac{sz_i}{2}]+\sum_{i<j} \gcd(sz_i,sz_j))

接下来，就是枚举置换，容易发现，我们应该按照 $sz$ 来枚举，也就是将 $n$ 拆分为若干个 $sz$ 。这就是 A000041， $n=49$ 数量级 $10^5$ ，可以接受，听其他题解说增长速率是 $O(\frac{e^{\sqrt{n}}}{n})$ ，到后面增速较快，然而 $n=60$ 时还算比较小。

拆分成若干大小递增的 $sz$ 后，首先，我们还是使用一次多重集的排列，如 $sz=\{1,1,2,3\}$ ，就将 $n$ 个节点分为红、黄、蓝、绿四部分，每部分的大小分别为 $sz$ 中的大小。

其次，我们观察到两个 $1$ 的形式是相同的，所以我们要多除 $2!$ 。

用数学的语言描述，我们记录 $buc_i$ 代表 $i$ 在 $sz$ 中的出现次数，那么到目前为止我们的方案数是：

\frac{n!}{\prod sz_i ! \prod buc_i !}

然而，我们注意到循环置换内的方案数我们没有考虑。大小为 $n$ 的循环置换内部排列的方案数为 $n-1$ 吗？答案是否定的。事实上，我们固定一个节点，剩下的节点随意排列，连起来即可，方案数是 $(n-1)!$ ，于是真实的方案数是：

\frac{n!}{\prod sz_i ! \prod buc_i !} \prod (sz_i-1)!

注意我们可以将方案数加起来，看是否为 $n!$ ，进行检验。

#include <bits/stdc++.h>
#define MAXN 65
#define MOD 997
using namespace std;
inline int read(){
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-') f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		x=x*10+ch-'0';
		ch=getchar();
	}
	return x*f;
}
int sz[MAXN],top,buc[MAXN];
int fac[MAXN],invfac[MAXN];
int ksm(int b,int k){
	int ans=1;
	while (k){
		if (k&1) ans=ans*b%MOD;
		b=b*b%MOD;
		k>>=1;
	}
	return ans;
}
int ans,all;
void dfs(int n,int lst){
	if (n==0){
		int t=0,prod=fac[all];
		for (int i=1;i<=all;++i) buc[i]=0;
		for (int i=1;i<=top;++i){
			buc[sz[i]]++;
			(prod*=invfac[sz[i]])%=MOD;
			t+=(sz[i]/2);
		}
		for (int i=1;i<=all;++i){
		 	(prod*=invfac[buc[i]])%=MOD;
		}
		for (int i=1;i<=top;++i){
			(prod*=fac[sz[i]-1])%=MOD;
		}
		for (int i=1;i<=top;++i){
			for (int j=i+1;j<=top;++j){
				t+=__gcd(sz[i],sz[j]);
			}
		}
		(ans+=prod*ksm(2,t)%MOD)%=MOD;
		return ;
	}
	for (int num=lst;num<=n;++num){
		sz[++top]=num;
		dfs(n-num,num);
		top--;
	}
}
int main(){
	all=read();
	fac[0]=1,invfac[0]=1;
	for (int i=1;i<=all;++i) fac[i]=(fac[i-1]*i)%MOD,invfac[i]=ksm(fac[i],MOD-2);
	dfs(all,1);
	printf("%d\n",ksm(fac[all],MOD-2)*ans%MOD);
	return 0;
}