微积分基本定理

原函数

$I \in D_f,\exists F(x),s.t. \forall x \in I,F'(x)=f(x)$ 称 $F(x)$ 是 $f(x)$ 在 $I$ 上的一个原函数。由罗尔定理的推论，我们知道如果 $F(x)$ 是 $f(x)$ 在 $I$ 的一个原函数，则 $F(x)+C$ 是 $f(x)$ 在 $I$ 的全体原函数。

变上限积分

$\Phi(x)=\int_a^x f(t)\mathrm{d}t$

1. 若 $f \in R[a,b]$，则 $\Phi \in C[a,b]$。

如果可积则有界，利用连续的定义 $I=\lim_{\Delta x \to 0} \Phi(x+\Delta x)-\Phi(x)= \lim_{\Delta x \to 0}\int_{x}^{x+\Delta x} f(t) \mathrm{d} t$。

由夹逼，$- \lim _{\Delta x\to0}|\Delta x M| \le I \le \lim _{\Delta x\to0}|\Delta x M|$。那么 $I=0$。

2. 若 $f \in C[a,b]$，则 $\Phi \in D[a,b]$。其导数为 $f(x)$。

也是利用导数定义，

$\Phi'(x)=\lim _{\Delta x \to 0} \frac{\Phi(x+\Delta x)-\Phi(x)}{\Delta x}=\lim_{\Delta x \to 0} \frac{\int_{x}^{x+\Delta x} f(x)}{\Delta x} = \lim_{\Delta x \to 0} \frac{f(\xi)\Delta x}{\Delta x}=f(x)$

注意这里我们使用积分中值定理的条件是 $f \in C[a,b]$。但是，$f$ 连续可以推 $\Phi$ 可导，$\Phi$ 可导不能推 $f$ 连续。反例：$f=\sin \frac{1}{x},x\not=0;0,x=0$。

这样，我们可以得知 $\frac{\mathrm{d} \Phi(u)}{\mathrm{d} u} = f(u)$，其中 $u$ 是表达式。例如：

$\frac{\mathrm{d}}{\mathrm{d} x} \int_{\Psi(x)}^{\varphi(x)} f(t)\mathrm{d}t= \frac{\mathrm{d}}{\mathrm{d} x} (\int_{0}^{\varphi(x)} f(t)\mathrm{d}t-\int_{0}^{\Psi(x)} f(t)\mathrm{d}t)\\=\frac{\mathrm{d\varphi(x)}}{\mathrm{d} x}\frac{\mathrm{d}}{\mathrm{d} \varphi(x)} \int_{0}^{\varphi(x)} f(t)\mathrm{d}t - \frac{\mathrm{d\psi(x)}}{\mathrm{d} x}\frac{\mathrm{d}}{\mathrm{d} \psi(x)} \int_{0}^{\psi(x)} f(t)\mathrm{d}t \\ =f[\varphi(x)] \varphi'(x)-f[\Psi(x)] \Psi'(x)$

注意点：被积函数只能与积分变量有关，如果存在 $x$ 要先提出来。

变限积分导数和函数的关系

1. 有可去间断点 $x_0$，如 $f(x)=1,x=0;0,x\not=0$，存在一个可去间断点 $0$，则 $\Phi(x)$ 可导，而且导函数是补全可去间断点所得到的的函数，相当于抹平，因为一点处的函数值影响可以忽略不计。
2. 有跳跃间断点 $x_0$，例如 $sgn(x)$，则在 $x_0$ 处 $\Phi(x)$ 不可导。
3. 奇偶性：$f(x)$ 奇函数推出 $\Phi(x)$ 偶，但是 $f(x)$ 偶，当 $\Phi(x)$ 下限为 $0$ 时，才能断定 $\Phi(x)$ 奇，事实上，当 $\int_0^a f(x)\mathrm d x=0$ 时，才能说明是奇函数。
4. $f(x)$ 周期 $T$，$\int_0^T f(x)\mathrm d x=0$ $\Leftrightarrow $ $\Phi(x)$ 周期 $T$。

处理积分式的技巧

可以把表达式塞进积分号里，也可以利用积分中值定理将积分转化为表达式，例如

$(x-a)f(x)-\int_a^x f(t)\mathrm{d}t=\int_a^x (f(x)-f(t)) \mathrm{d} t = (f(x)-f(\xi))(x-a)$

也可以变动主元，变动主元之后，可以得到额外的函数值信息，例如 $f(x) \in C[a,b]$，证明：

$2 \int _a^b f(x) (\int_x^b f(t) \mathrm{d} t) \mathrm{d} x =(\int_a^b f(x) \mathrm{d} x)^2$

发现可以将 $a$ 或者 $b$ 看做变量，但是将 $b$ 看为变量，积分号里面存在变量，于是只能将 $a$ 看成变量，两边关于 $a$ 求导。

$-2f(x) (\int_x^b f(t) \mathrm{d} t)|_{x=a} = -2 f(x)\int_a^b f(x) \mathrm{d} x$

导数值相等，再不妨令 $a=b$，则就可以得到原式相等。

分部积分：

$2\int_a^b \int_x^b f(t)\mathrm d t \mathrm d\int_x^b f(u)\mathrm d u$

$f(x) \in D[0,1],f(0)=0$，且当 $x \in (0,1)$ 时，$0 < f'(x) <1$ ，当 $a \in (0,1)$ 时，证明：

$(\int_0^a f(x) \mathrm{d} x)^2 > \int_0^a f^3(x) \mathrm{d} x$

构造 $F(a)=(\int_0^a f(x) \mathrm{d} x)^2 - \int_0^a f^3(x) \mathrm{d} x$，则 $F(a)=0$：

$F'(a)=2 f(a) \int_0^a f(x) \mathrm{d} x - f^3(a)=f(a)[2\int_{0}^a f(x) \mathrm{d} x-f^2(a)]$

继续求导，$F'(a)=0$：

$G(a)=2\int_{0}^a f(x) \mathrm{d} x-f^2(a),G'(a)=2f(a)(1-f'(a))>0$

因为 $G(0)=0$，所以 $G(a)>0,a\in(0,1)$，推出 $F'(a) >0,a\in(0,1)$，推出 $F(a)>0,a\in(0,1)$。

若 $f(x) \in C[a,b]$ 且单增，求证：

$\int_a^b xf(x)\mathrm d x\ge\frac{a+b}{2} \int_a^b f(x)\mathrm d x$

以 $b$ 为主元。

视角变化，将积分题转换为微分题

$f(x) \in D^2 [a,b],f^{(2)}(x) \in C[a,b]$，证明 $\exists \eta \in [a,b],s.t.$：

$\int_{a}^b f(x)\mathrm{d} x =\frac{f(a)+f(b)}{2}(b-a) -\frac{(b-a)^3}{12} f''(\eta)$

我们可以将左边看为 $F(b)-F(a)$，右边导数全部加一阶。

令 $\varphi(x)=F(x)-F(a) - \frac{F'(x)+F'(a)}{2}(x-a),\psi(x)=-\frac{(x-a)^3}{12}$，多次使用柯西即可。当然原函数不一定存在，严格证明还是要用变上限那一套。

$f(x) \in C[0,1]$，且 $I=\int_0^1 f(x) \mathrm d x \not=0$，证明 $\exists 0<x_1<x_2<1,s.t.$

$\frac{1}{f(x_1)}+\frac{1}{f(x_2)} = \frac{2}{I}$

令 $F(x)=(\int_0^x f(t) \mathrm d t)/I$，则 $F(0)=0$，$F(1)=1$，且 $F(x) \in C[0,1]$得到：

$\frac{1}{F'(x_1)}+\frac{1}{F'(x_2)}=2$

由于连续函数的介值性定理，$\exists \alpha \in [0,1],s.t. F(\alpha)=\frac{1}{2}$，则：

$F'(x_1)=\frac{F(\alpha)-F(0)}{\alpha -0},F'(x_2)=\frac{F(1)-F(\alpha)}{1-\alpha}$

即证。

原函数存在性

若 $f \in C[a,b]$，则 $f(x)$ 存在原函数 $F(x)$，这是因为对应的 $\Phi(x)$ 存在而且可导，但是 $f\in R[a,b]$ 不一定推出存在原函数，因为 $f$ 需要满足导函数的性质，例如 $f=\mathrm {sgn}$ 就存在第一类间断点，不是一个函数的导函数，然而 $f \in R[a,b]$。我们也不能说 $\Phi$ 是 $f$ 的原函数，因为 $\Phi$ 不一定可导，例如 $\Phi(x) = \int _{-1} ^x \mathrm{sgn}(x) \mathrm{d}x=|x|-1,x \ge 0$，然而 $\Phi$ 在 $x=0$ 不可导，因此不是 $f$ 的原函数，我们也不能肯定 $\Phi$ 的导函数就是 $f$。存在原函数也不一定可积，比如 $f(x)=2x\sin\frac{1}{x^2} -\frac{2}{x} \cos \frac{1}{x^2} , 0<x\le1;0,x=0$ 是 $F(x)=x^2 \sin \frac{1}{x^2}, 0 < x \le 1;0,x=0$ 的导函数，但是 $f(x)$ 无界不可积。

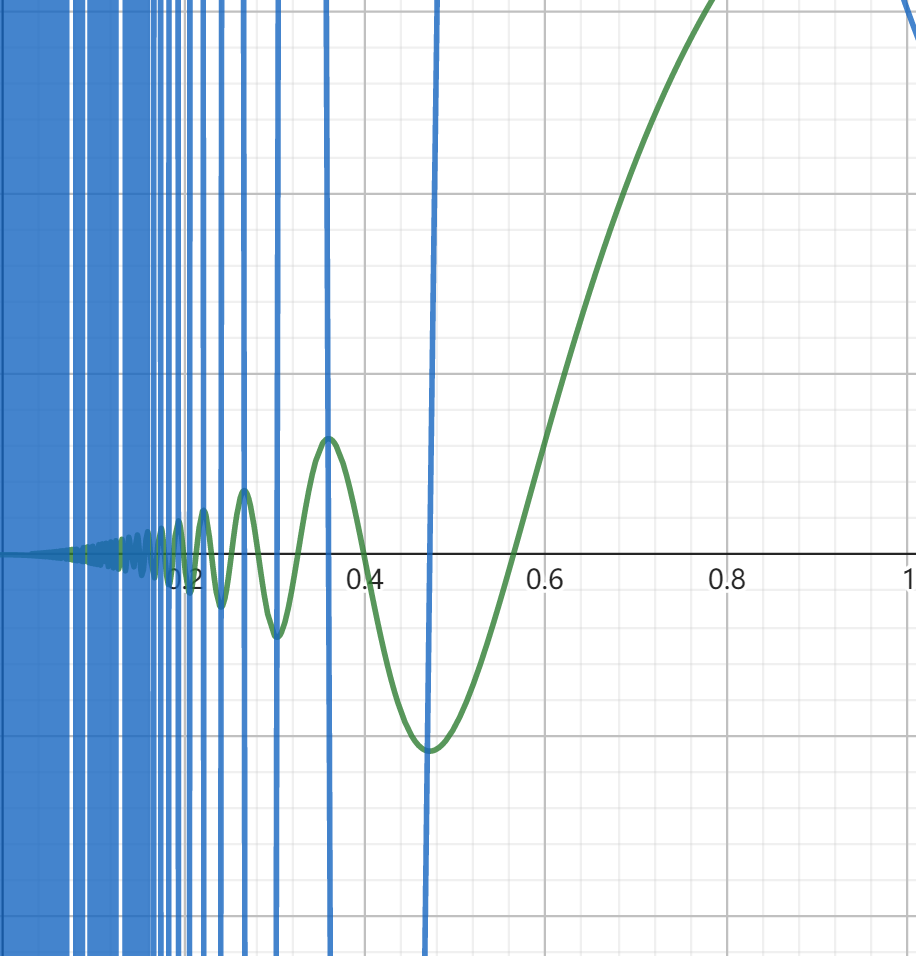
如图，$F(x)=x^2\sin\frac{1}{x^2}$ 虽然看似波动范围越来越小，实则波动的幅度越来越大，导致 $F'(x)$ 当 $x \to 0$ 无界，但是 $F'(0)$ 存在且为 $0$。

总结：可积不一定要有原函数，有原函数也不一定可积。

1. 闭区间连续函数必然存在原函数，必然可积，因为有界。
2. 如果函数在闭区间内部存在第一类间断点或者无穷间断点则必不存在原函数。但是震荡间断点可以存在原函数。
3. 改变或者删除有限个点的函数值不影响原来函数的积分特性。

牛顿-莱布尼兹公式

强条件：设 $f \in C[a,b]$，$F(x)$ 是 $f(x)$ 在 $[a,b]$ 上的一个原函数，则有：

$\int_a^b f(x) \mathrm d x=F(b)-F(a)$

因为变限函数 $\Phi(x)=\int_0^x f(x) \mathrm d x$（不妨设），然后 $\Phi(x)$ 是 $f(x)$ 在 $[a,b]$ 上的一个原函数，则 $F(x)=\Phi(x)+C$，即可推出原式。

弱条件的牛顿-莱布尼兹公式：

$f \in R[a,b]$，$F(x) \in C[a,b]$ 是 $f(x)$ 在 $(a,b)$ 内的一个原函数，即对 $\forall x \in (a,b)$ 有 $F'(x)=f(x)$，则：

$\int_a^b f(x) \mathrm d x=F(b)-F(a)$

这里条件减弱为 $f \in R[a,b]$。

对于右端点取不到的情况，令 $\Phi(x)=\int_a^x f(x) \mathrm d x$，由 $\Phi(x)$ 连续（是因为 $f \in R[a,b]$），得 $\int_a^b f(x) \mathrm d x=\lim_{x \to b} \Phi(x)=\lim_{x \to b} F(x)-F(a)=F(b)-F(a)$（这里运用 $F(x)$ 连续）

然后左端点和右端点都取不到的情况与之类似。

对比：$f(x) \in C/R[a,b]$，是否 $F(x) \in C[a,b]$。原因是如果 $f(x) \in R[a,b]$，不能保证 $F(x)=\Phi(x)$。

不满足处处有定义的做法

进行积分拆分：

$f(x)=\frac{(x+1)^2(x-1)}{x^3(x-2)},I=\int_{-1}^3\frac{f'(x)}{1+f^2(x)}\mathrm d x$

$\arctan f(x)|_{-1}^{0}+|_{0}^{2}+|_{2}^3$

带定积分的函数方程

切入点，定积分看为常数 $A$，然后对 $f$ 积分结果为 $A$ 即可求解。

与积分中值定理结合

$f(x) \in C[0,1]$，且 $\int_0^1 f(x)\mathrm d x =0$，$\int_0^1 xf(x)\mathrm d x=1$，试证：

$\exists x_0 \in [0,1],s.t. |f(x_0)|>4\\ \exists x_1 \in [0,1],s.t. |f(x_1)|=4$

如何构造中值，考虑 $\int_0^1(x-\frac{1}{2})f(x)\mathrm d x=1$：

$1=|\int_0^1(x-\frac{1}{2})f(x)\mathrm d x| \le \int_0^1|(x-\frac{1}{2})||f(x)|\mathrm d x$

因为 $|x-\frac{1}{2}|$ 在 $[0,1]$ 上不变号，而且 $|f(x)|$ 在 $[0,1]$ 上连续（就是为什么要取绝对值，而且结论也暗示我们取绝对值）

由积分中值定理，

$\int_0^1|(x-\frac{1}{2})||f(x)|\mathrm d x = |f(\xi)| \int_0^1|(x-\frac{1}{2})|\mathrm d x \ge 1$

得 $|f(\xi)| \ge 4$，下面开始分析两个结论，如果全部 $|f(x)| = 4$，则第一个条件不满足，然而这样的情况下，加上 $f(x) \in C[0,1]$ 的条件，$\int_0^1 f(x) \mathrm d x \not=1$，因此，第一个条件得证，如果全部 $|f(x)|>4$，回推不等式，要求所有的 $(x-\frac{1}{2}) f(x)$ 同号，然而 $f(x)$ 一定要在 $\frac{1}{2}$ 点变号，这与 $f(x)$ 连续的条件矛盾！

因此，第一个和第二个结论都满足。