基础的方程:
−kx=mdt2d2x
dt2d2x+:=ω2mkx=0
dt2d2x=−ω2x
x=Asin/cos(ωt+φ)
x=Aei(ωt+φ)
简谐振动运动学
振动是一种普遍存在的运动形式
- 物体的来回 往复运动(弹簧振子、单摆等)Vibration, Oscillation.
- 电流、电压的周期性变化
任一物理量(如位移、电流等)在某一数值附近反复变化----振动。
机械振动: 物体在一定位置附近作来回往复的运动
可以证明: 任何复杂的振动都可以认为是由若干个简单而又基本的振动的合成。这种简单而又基本的振动形式称为简谐振动。

简谐振动的运动规律

简谐振动:凡质点的运动遵从余弦(或正弦)规律时,其运动形式为简谐振动。
x=Acos(ωt+φ)
-
振幅 A Amplitude.
-
周期 T 完成一次全振动所经历的时间。
-
频率 ν:单位时间内完成全振动的次数。
-
角频率 ω
-
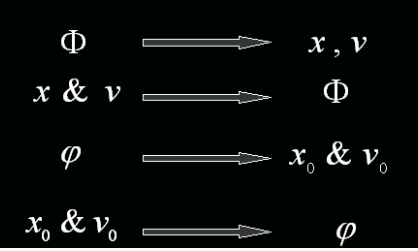
相位 Φ=(ωt+φ) 位置和速度仅仅由相位决定 x=AcosΦ(t),v=−ωAsinΦ(t)。φ:振动的初相位。
求出 φ,Φ:
φ=arctan(−ωx0v0)Φ=arctan(−ωxv)

相位差 对于两同频率的谐振动 Δφ=φ2−φ1 初相差。明确 φ2−φ1 在 −π∼π 之间。
同相和反相 Δφ=±2kπ 同相,Δφ=±(2k+1)π 反相。
超前和落后

这里 φ2=0,φ1=−π/2,因此 x2 超前于 x1。
速度和加速度
x=Acos(ωt+φ)v=−ωAsin(ωt+φ)=vmcos(ωt+φ+2π)a=−ω2Acos(ωt+φ)=vmcos(ωt+φ±π)
- vm=ωA 称为速度幅,速度相位比位移超前 π/2。
- am=ω2A 称为加速度幅,和位移反相。


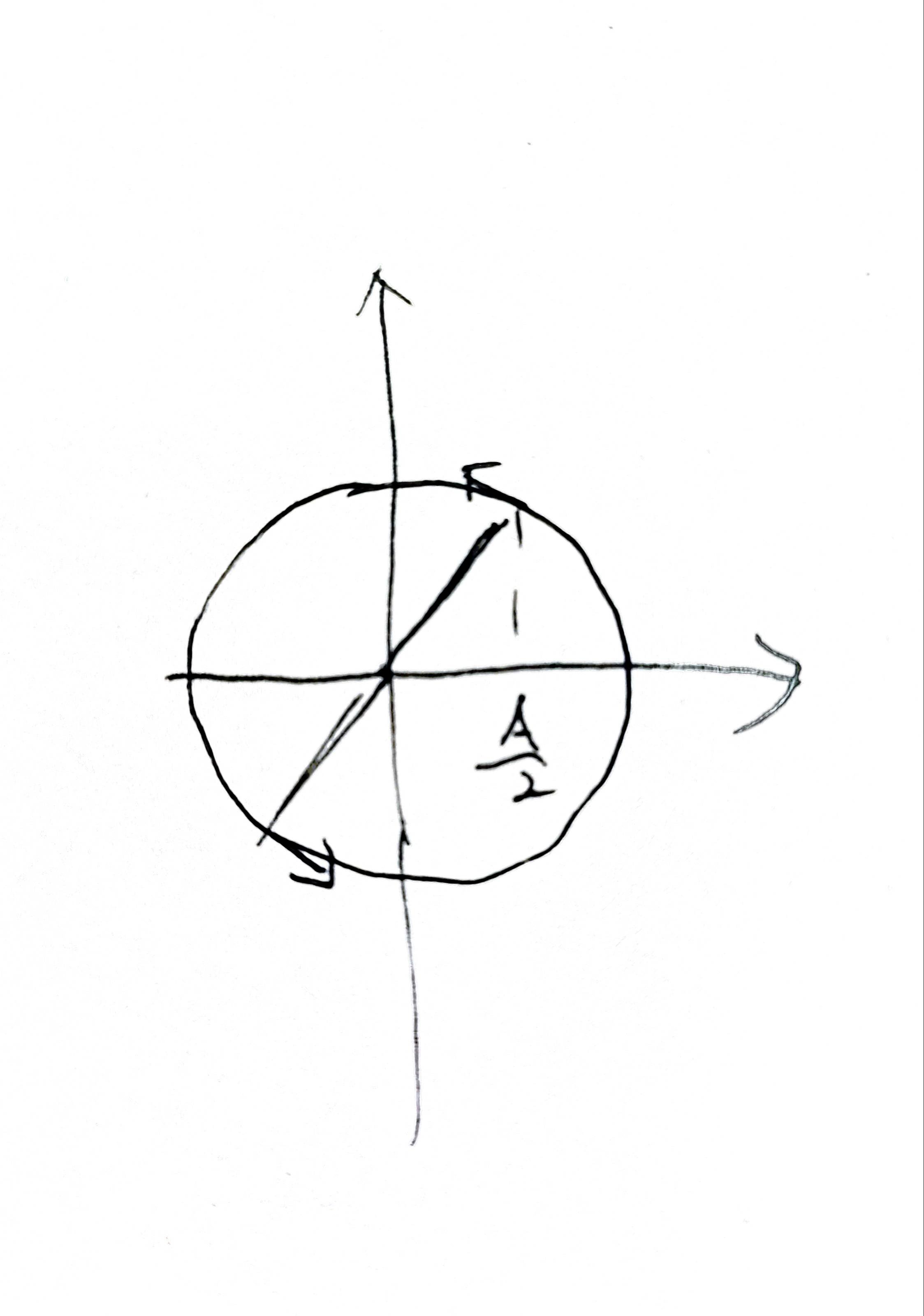
旋转振幅矢量法

x=Acos(ωt+φ)y=Asin(ωt+φ)

利用旋转矢量可以得出初相位(多个解),然后通过质点移动的方向,来判定是哪个初相位。

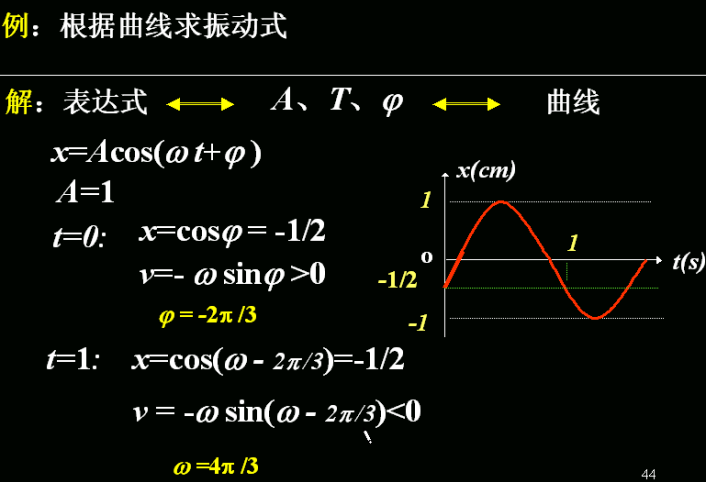
(1) 振动式 x−t 曲线。
已经知道 A=12 cm,角速度 ω=T/2π=π s−1。
振动式:x=0.12cos(πt−π/3)。
(2)

(3)

旋转矢量法。

简谐振动动力学
简写振动的动力学方程
受到线性恢复力 F=−kx,物体具有惯性。
dt2d2x+mkx=0⇒dt2d2x+ω2x=0
完全的积分法:
dt2d2x=dtdv=vdxdv=−ω2x
解为:
x=Acos(ωt+φ)
由初始条件 (x0,v0):
A=x02+ω2v02φ=arctan(−ωx0v0)
怎么推的?
x0=Acos(ωt+φ)∣t=0=Acosφv0=−ωAsin(ωt+φ)∣t=0=−ωAsinφ
因此
x02+ω2v02=A2(sin2φ+cos2φ)=A2
⇒A=x02+ω2v02φ=arctan(−ωx0v0)
如果存在常力 F ? 比如说重力或者电场力,位移振子。
mdt2d2x=−kx+F
mdt2d2(x−kF)=−k(x−kF)
令 X=x−x0,x0=F/k,得到
dt2d2X+mkX=0
满足 x=Acos(ωt+φ),也可以是受迫振动。
微振动的简谐近似
单摆在小角摆动
以角度增加的方向为正方向。那么重力分力:f=−mgsinθ。
由于 θ 很小,sinθ≈θ,而且走过的弧长 s=lθ,那么
f=−lmgs=−ks
得到是简谐振动的形式,因此
ω=mk=lg
周期
T=2πgl
复摆的小角摆动
定轴转动问题,固定 O 点,对应 z 轴。以角度增加的方向为正方向。
Mz=Jdt2d2θ
Mz=−mgrcsinθ≈−mgrcθ
因此
dt2d2θ+ω2θ=0
ω=mgrc/J
如果复摆就是一个质点,得到 J=mrc2,代入,得到 ω=g/l。
设水平方向 C 投影离原点距离为 x,则 θ≈x/rc,得到
Ep(x)=mgrc(1−cosθ)≈mgrc2θ2=2rcmgx2=21kx2
为什么能够近似简谐振动?
在最低点 x 处泰勒展开。
Ep(x)≈Ep(0)+=0dxdEpx+21dx2d2Epx2


对于板子,分析横向运动,需要分析摩擦力,因此需要分析支持力。选两个圆柱的中点为原点。
首先,受力平衡,得到 N1+N2=mg,其次不能发生转动,力矩平衡
N1(l+x)=N2(l−x)
得到
N1=2ll−xmgN2=2ll+xmg
f1−f2=ma⇒a=mμ(N1−N2)=−lxμg
得到
T=2πμgl
如何判别简谐振动?
动力学方程形式:x¨+ω2x=0 动力学方程形式。F合=−k∗x+F0 线性回复力。E=21k∗x2+21M∗v2 能量的形式。
简谐振动的能量
动能 Ek=21mv2=21kAsin2(ωt+φ)。
势能 Ep=21kx2=21kA2cos2(ωt+φ)。

习题
13-15

−mgRsinθ=JOθ¨
然后由平行轴定理得到 JO=JC+md2=mR2+mR2=2mR2。
当 θ 很小的时候,sinθ≈θ,得到
2mR2θ¨+mgRθ=0
对比
x¨+ω2x=0
可以得到
ω2=2mR2mgR=2Rg,ω=2Rg
T=ω2π=2πg2R
也可以使用能量,能量守恒。
E=−mgRcosθ+21JOθ˙2=−mgR+21mgRθ2+mR2θ˙2
对比能量的表达式:
21k∗x2+21m∗x˙2
等效的劲度系数与质量:k∗=mgR,m∗=2mR2。
ω=m∗k∗=2Rg
17-3

21-4


利用系统机械能

利用动力学方程
M=kΔl⋅L+mgΔl+21m′gΔlLΔl=θ
J=31m′L2+mL2
Jθ¨=−M
17-11

其实就是求周期。第 n 滴 M总=M+nm,求的
ω=M总k=M+nmk
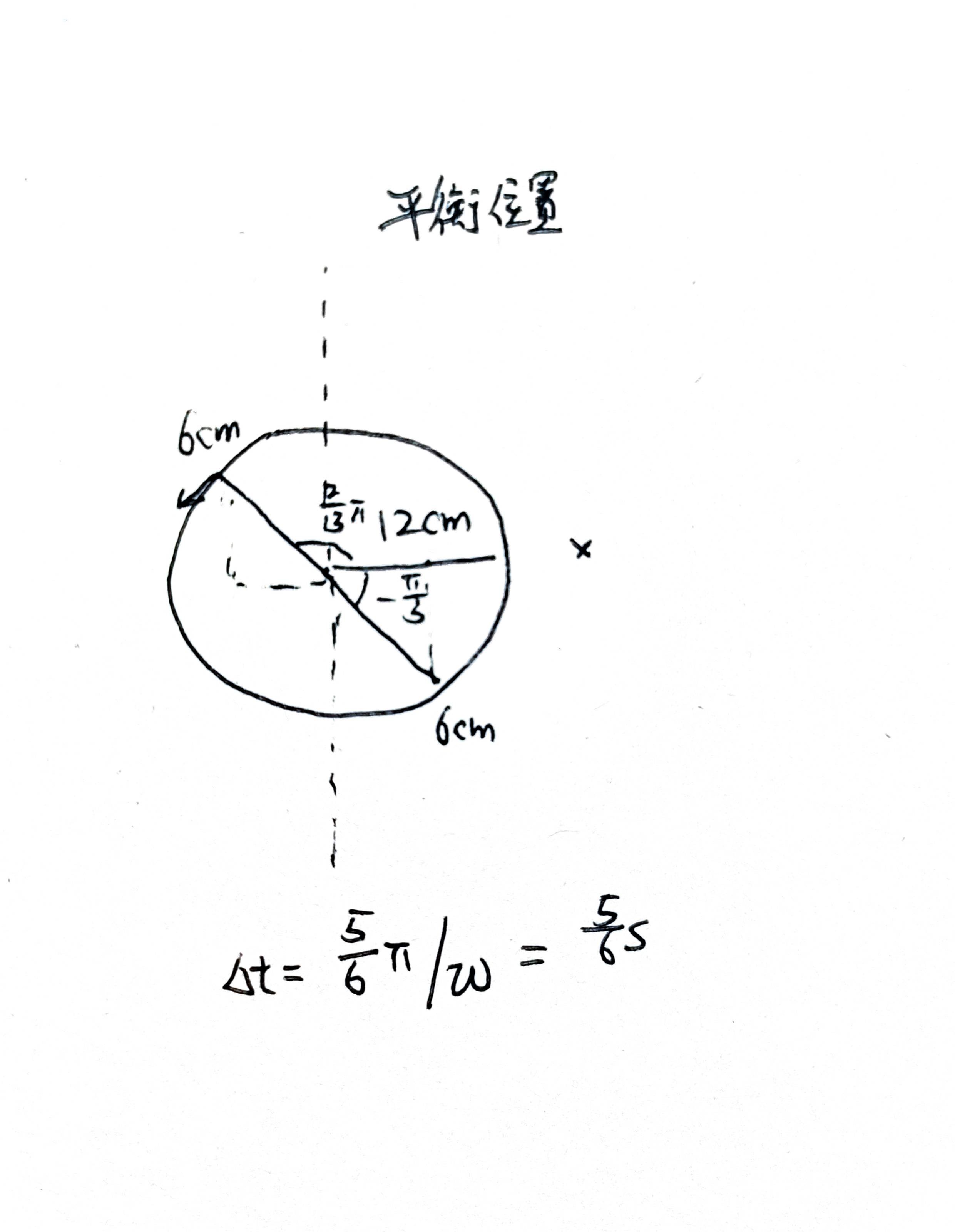
因此,走过 π,时间间隔
Δt=ωπ=πkM+nm
18-1

原题了。
12-2


可以直接说明平衡位置。







