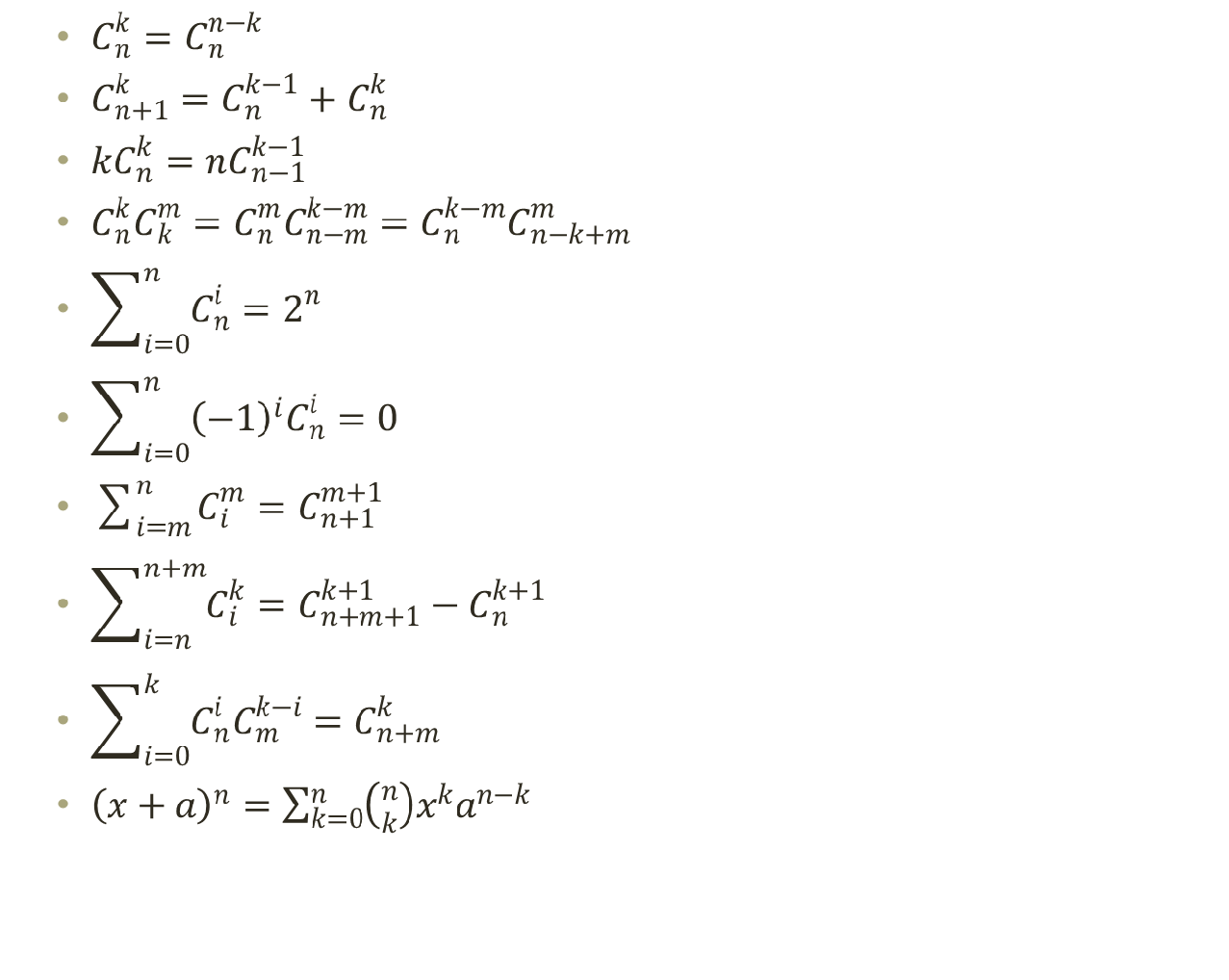组合数

都是一些定义吧。。。

性质$1.$，从$n$个东西中选$k$个选和选$n-k$个不选是一样的。
性质$2.$，从$n+1$个东西中选$k$个，可以在其中$n$个东西中选$k$个，剩下一个不选，也可以在其中$n$个东西中选$k-1$个，剩下一个选。
性质$2.$在预处理组合数时经常用到，如：

1
2
3
4
5
6

for (register int i=0;i<MAXN;++i){
    C[i][0]=1,C[i][i]=1;
    for (register int j=1;j<i;++j){
        C[i][j]=(C[i-1][j-1]+C[i-1][j])%MOD;
    }
}

还有一个神奇的性质，我们把$(x+a)^n$拆开，变成$(x+a)(x+a)....$发现$x$的系数为$k$时，相当于在$n$个$x$中选$k$个，剩下$n-k$个选$a$所以系数为$C_n^k$，所以，$(x+a)^n=\sum^n_{k=0}C^k_nx^ka^{n-k}$
根据这个性质，我们把$x=1$，$a=1$代入，发现$\sum^n_{i=0}C^i_n=(1+1)^n=2^n$。
把$x=1$，$a=-1$代入，发现$\sum^n_{i=0}(-1)^iC^i_n=(1+(-1))^n=0$

剩下的性质，自己脑补一些场景，也可以证明出来。

卡特兰数

所有奇卡特兰数，下标都满足$n=2^k-1$（不知道有啥用，手动狗头）

前$6$点基本上都是老生常谈了，长方形填充还是挺巧妙的。

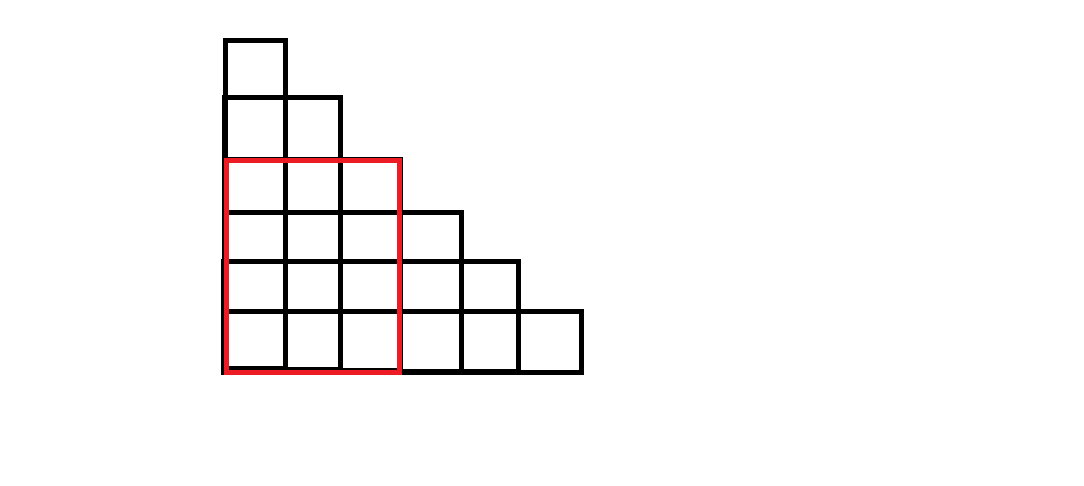
考虑一个可行的方案，必有如图的一个长方形，它的一个顶点在阶梯上，另一个在阶梯的最下面的角上（标成红色），要不然整个长方形不可能填充完。

发现它上方和右方的小阶梯可以构成子状态，$yy$一下，发现$F(n)=\sum^{n-1}_{i=0}{(F(i)+F(n-i-1))}$

这不就是卡特兰数吗？

GCD&LCM

大家都知道$gcd(x,y)$=$gcd(y,x\mod y)$，我们可以用如下的算法求$gcd$。

1

int gcd(int x,int y){return x%y==0?y:gcd(y,x%y);}

我们发现一个数对一个小于它的数取模后至少缩小一半，所以算法复杂度为$log(n)$，实际可能还更小。

拓展欧几里得算法

求$ax+by=c$的正整数解。
首先根据裴蜀定理，我们知道：$gcd(a,b)|c$，否则方程无解。
设d=\\dfracc}{gcd(a,b)}，则知道$ax+by=gcd(a,b)$的解，我们把解出的$x,y$都乘个$d$就能得出原方程的解$x',y'$。

考虑把问题简单化，只求$ax+by=gcd(a,b)$的正整数解。
考虑如下的方程：
$ax_1+by_1=gcd(a,b)$
$bx_2+(a\mod b)y_2=gcd(b,a\mod b)$

我们知道$gcd(a,b)=gcd(b,a\mod b)$
所以$ax_1+by_1=bx_2+(a\mod b)y_2$
又知道$a\mod b=a-\lfloor a/b \rfloor \times b$
我们把上面的柿子代入：
发现$ax_1+by_1=bx_2+(a-\lfloor a/b \rfloor \times b)y_2$
化一下：$ax_1+by_1=ay_2+b(x_2-\lfloor a/b \rfloor \times y_2)$
对比两边系数，我们开心地发现$x_1=y_2$，$y_1=x_2-\lfloor a/b \rfloor \times y_2$，于是我们可以根据$x_2,y_2$算出$x_1,y_1$

具体实现的时候，递归求解即可。

模板：

1
2
3
4
5
6
7
8
9
10
11

int gcd(int a,int b,int &d,int &x,int&y){
    if(!b){
        d=a,x=1,y=0;
        return x;
    }
    else{
        gcd(b,a%b,d,y,x);
        y-=x*(a/b);
    }
    return x;
}

BSGS （北上广深算法）

已知$a,b,p$，求$a^x=b(\mod p)$的正整数解。

考虑折半法，我们设$B=\sqrt{P}$，将$x$化为$B \times i-j$的形式，其中$i<B,j<B$
将$x$代入原柿子，发现$a^x=a^{B \times i-j}=a^{B \times i} / a^j$
把那个$a^j$搞到右边，发现$a^{B \times i}=b \times a^j$
其中，左右两边只有$i,j$两个变量，取值只有$B$种可能。
考虑把$b \times a^j$预处理出来，丢进一个$map$或哈希表里面。
后面一个一个枚举$a^{B \times i}$，查询$map$或哈希表里面有没有。

思维比较简单，但是代码比较长。
时间复杂度$O(\sqrt {n})$

模板题：P2485 [SDOI2011]计算器

题解：
对于询问$1.$，快速幂即可。
对于询问$2.$，逆元即可，注意判断不存在的情况。（当然$extgcd$也是可做的）
对于询问$3.$，需要运用$BSGS$算法，具体实现时需要注意$B \times i-j$可能为负，需要$+p$再取模，并且$j=0$，$b \times a^j=b$也是合法的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85

#include <bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
    int x=0,f=1;
    char ch=getchar();
    while (ch<'0'||ch>'9'){
        if (ch=='-') f=-1;
        ch=getchar();
    }
    while (ch>='0'&&ch<='9'){
        x=(x<<3)+(x<<1)+(ch^'0');
        ch=getchar();
    }
    return x*f;
}
int p;
inline int ksm(int b,int k){
    int ans=1;
    while (k){
        if (k&1) ans=(ans*b)%p;
        b=(b*b)%p;
        k>>=1;
    }
    return ans;
}
inline void Solve1(int T){//快速幂
    while (T--){
        int y=read(),z=read();p=read();
        y%=p;
        printf("%lld\n",ksm(y,z));
    }
}
inline void Solve2(int T){//逆元
    while (T--){
        int y=read(),z=read();p=read();
        y%=p,z%=p;
        if (y==0&&z!=0){
            printf("Orz, I cannot find x!\n");
            continue;
        }
        printf("%lld\n",ksm(y,p-2)*z%p);
    }
}
map<int,int>M;
inline void BSGS(int a,int b){
    if (a==0&&b!=0){
        printf("Orz, I cannot find x!\n");
        return ;
    }
    int B=(int)sqrt(p);
    M.clear();
    int now=b%p;
    M[now]=0;
    for (register int i=1;i<=B;++i){
        now=(now*a)%p;
        M[now]=i;
    }
    now=1;
    int S=ksm(a,B);
    for (register int j=1;j<=B;++j){
    //判断a^{B \times i}是否在表中
        now=(now*S)%p;
        if (M.count(now)){
            int ans=j*B-M[now];//M[now]=i
            printf("%lld\n",(ans%p+p)%p);
            return ;
        }
    }
    printf("Orz, I cannot find x!\n");
}
inline void Solve3(int T){//BSGS
    while (T--){
        int y=read(),z=read();p=read();
        BSGS(y%p,z);
    }
}
#undef int
int main(){
#define int long long
    int T=read(),K=read();
    if (K==1) Solve1(T);
    else if (K==2) Solve2(T);
    else Solve3(T);
}

EXCRT 扩展中国剩余定理

在中国剩余定理的基础上，膜数$p_1,p_2,p_3...,p_n$可能不是质数：
假设现在我们已经求出前$k-1$个方程的解了，设为是$x$：
设$M=lcm(p_{1},p_{2},....p_{k-1})$，那么我们发现前$k-1$个方程的通解可以表示成$x+M \times alb$(这些解都可以成立)，其中$alb$是整数。
我们要求$t$，使得$x+M \times t=a_k (\mod p_k)$，也就是$M \times t =a_k-x(\mod p_k)$
可以用$extgcd$求解$t$，解完$t$后，就发现前$k$个式子的一个解为$x+t \times M$

整体思路也就是把式子合并合并再合并。

话说这个东西和$CRT$关系好像不是很大。

高斯消元

可以求解类似于

$a_{11} \times x + a_{12} \times y + a_{13} \times z ....... = b_1$

$a_{21} \times x + a_{22} \times y + a_{23} \times z ....... = b_2$

$a_{31} \times x + a_{32} \times y + a_{33} \times z ....... = b_3$

$........................................$

$........................................$

的方程。

假设我们有三个式子，假设$alb$为现在未知数个数，现在$alb$为$3$：

$1 \times x + 2 \times y + 3 \times z = 4 ... (1)$

$2 \times x + 3 \times y + 4 \times z = 5 ... (2)$

$3 \times x + 4 \times y + 7 \times z = 6 ... (3)$

我们把$(1)$中的$x$设为主元，和$(2)(3)$式相减。

$(2)-(1) \times 2 : -1 \times y + -2 \times z = -3 ... (4)$

$(3)-(1) \times 3 : -2 \times y + -2 \times z = -6 ... (5)$

发现$alb=2$，继续执行一遍类似的操作，把$(4)$中的$y$设为主元，和$(5)$式相减。

$(5)-(4) \times 2 : 2 \times z = 0$

我们就成功地解出了$z$，把$z$往上带，可以求出$x$，$y$，就可以解出方程。
不仅对于$alb=3$的情况，$alb$更大，也可以用类似的方法求出未知数。
时间复杂度$O(alb^2)$
高斯消元的操作可以转换为矩阵操作，其实就是把一个普通矩阵转换为单位矩阵。

逆矩阵

单位矩阵$e$：只有主对角线为$1$的矩阵
容易发现单位矩阵乘任意矩阵，任意矩阵乘单位矩阵都为其本身
于是定义一个$n\times n$的矩阵$A$的逆矩阵为$A^{-1}$满足$A \times A^{-1}=e$;若$B \times A=C$,则$B=C*A^{-1}$
矩阵初等变换：交换两行/列，将一行/列的若干倍加到另一行/列上去（这些操作都可以通过左乘初等变换矩阵实现）
那么可以把$A$搞成$e$的变换矩阵就是$A^{-1}$了
过程就是高斯消元，开始在原矩阵的旁边维护一个$e$
对原矩阵的操作，都对这个矩阵也做一次
这样当$A$变成$e$了，原来的这个$e$就变成$A^{-1}$了

我们可以把操作矩阵定义为$C_1,C_2,...C_k$，发现$A \times C_1 \times C_2 \times C_3 ... \times C_k=e$，
由于矩阵支持结合律，我们可以在这个式子两边同时乘以$A^{-1}$，发现$A \times A^{-1} \times C_1 \times C_2 \times C_3 ... \times C_k=e \times A^{-1}$
由于上面的两条性质$A \times A^{-1}=e$和$A \times e = A$，我们可以将式子化为$e \times C_1 \times C_2 \times C_3 ... \times C_k = A^{-1}$

所以原来的$e$就变为$A^{-1}$了，是不是很巧妙？

拉格朗日插值法

全然わからない！，似乎是一个构造函数的神奇方法，留个坑待填。

一道小水题 P4986