一个非常有趣的结论:
Raney引理:
给你一个数列ai(1≤i≤n),而且定义Si=∑i=1nai,并且Sn=1,求证ai的循环排列里面有且仅有一个序列,满足∀i∈[1,n],Si>0。
循环排列的意思也非常好理解。
举一个例子:a=1,4,−5,3,−2,0
循环排列为:
- <1,4,−5,3,−2,0>
- <4,−5,3,−2,0,1>
- <−5,3,−2,0,1,4>
- <3,−2,0,1,4,−5>
- <−2,0,1,4,−5,3>
- <0,1,4,−5,3,−2>
显然对于这组数据来说,4是满足条件的。
如何证明?
看到这类环上的问题,首先考虑拆环成链。
考虑一个无限的数列b=a1,a2,a3,...an,a1,a2,a3,...an,a1,a2...
对于这个数列,再做一次前缀和,设fx=∑i=1xa[i]
注意到fx+n−fx=fn=1,所以这个函数每过n格就会整体向上平移一格:
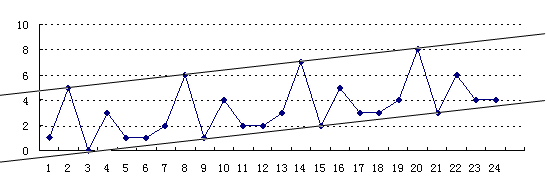
资料来源:浅谈数形结合思想在信息学竞赛中的应用
可以看图理解。
于是我们可以构造斜率为\frac{\dfrac的两条直线"夹住"原函数。
可以发现每过n个点,下面那条直线就会和函数相切一次。
从那个切点(图中为(3,0))向上走,发现所有的Si都>0,因为函数不可能和下面的直线相交。
同时在每n个点中,有且仅有一个点和直线相切(因为每过n个点函数才会经过一次整点),这就证明了唯一性。
思考,Sn!=1时,为什么不能说明唯一性?
因为Sn!=1时,斜率为\fra\dfrac}{n},不能保证一定只经过一个整点。
比如Sn=2,n=6时,就会发现会有矛盾。




