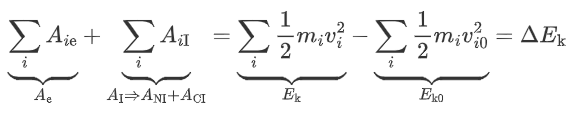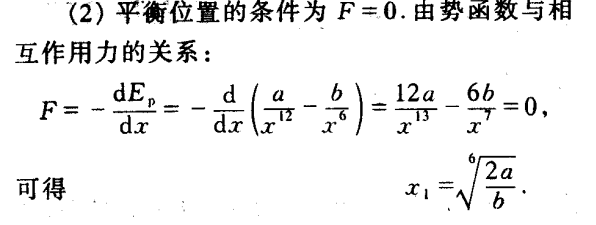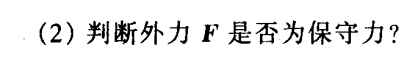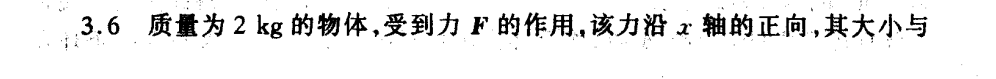牛顿第二定律分析了物体运动的过程。但是想要分析力的累积效应,从空间和时间的角度来看,对物体运动状态的改变。
- 力的时间积累:冲量。
- 力的空间积累:做功。
F=ma=mdtdv
F=mdtdv⇒mdv=Fdt
时间积累效应。
∫tatbFdt∫tatbF⋅dr
功 质点动能定理
功
衡力的功:
A=F⋅Δr
变力的功:
A=FΔrcosθ
A=∫abF⋅dr=∫abFcosαds
路径积分。积分有没有近似?位移与参考系有关系。
摩擦力做功:
Ff=−μmgetA=∫abFf⋅dr=−FfSab
摩擦力做功与路径有关。
动能定理
F⋅dr=mdtdv⋅dr=mdrdvdtdr⋅dr=mv⋅dv=md(21v⋅v)
物体具备某一个速度,就具备了某种能力,就是 21mv2。kinetic energy.
dA=F⋅dr=md(21v⋅v)=dEk
Aab=∫abF⋅dr=∫abdEk=Ekb−Eka
动能定理只在惯性系中成立。
牛顿力学的 Ek。自然界的动能是不是?
Ek=21mv2=mc2−m0c2
m=1−v2/c2m0
本来的面目。
功率
P=dtdA=F⋅v
保守力 非保守力 耗散力
力场
F=F(r,t,v)
当质点所受的力仅与位置有关,即
F=F(r)
时,代表了质点受力的空间分布,称为力场。
有心力 始终通过以固定的点的力。
F=F(r)=f(r)er
库仑力和万有引力,弹性力。力的方向容易定。
有心力的功:
∫ABF1⋅Δr1=∫ABf(r)∣Δr1∣cosθ1=∫ABf(r)Δr
沿着任意闭合回路做功均为 0。
万有引力
F=−r3GMmr
在极坐标系中:
r=rerdr=drer+rdθeθ⇒r⋅dr=rdr
∫ABF⋅Δr=∫AB−r3GMmr⋅dr=∫AB−r2GMmdr=−rAGMm+rBGMm
弹性力
A=∫F⋅dx=∫x1x2−kxi⋅dxi=−∫x1x2kxdx=21kx12−21kx22
惯性离心力
回旋力
F=βreθA=∫abF⋅dr
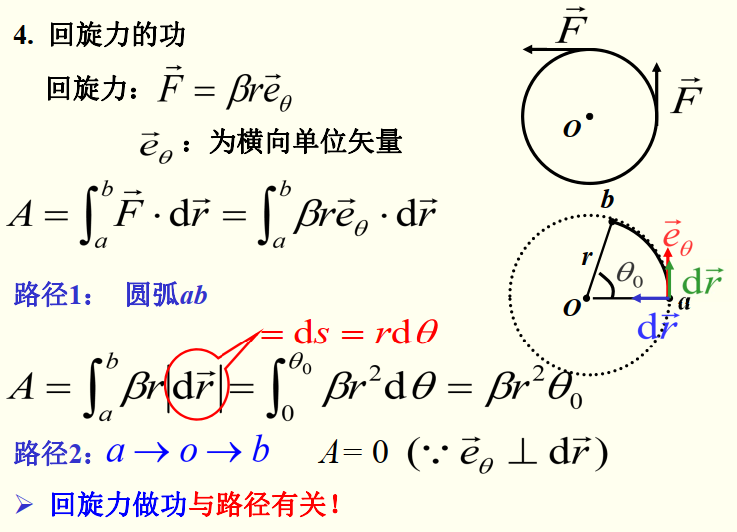
摩擦力
一对摩擦力 所做总功与参考系无关。
一对力的功 作用力和反作用力。
A=∫A1,B1A2B2f12⋅dr1+f21⋅dr2=∫A1,B1A2B2f21⋅d(r2−r1)=∫A1,B1A2B2f21⋅元相对位移dr21
如果选择 1 为参考系:
A=∫A1,B1A2B2f21⋅dr2
一对力的做功于参考系无关。
r=ro+r′dr1=dro+dr′dr2=dro+dr′dr21=dr2−dr1=dr21′
关键是相对。选物体 1 为参考系。
注:无相对位移或相对位移与一对力垂直。
保守内力:Aab=−(Ep(rb)−Ep(ra))
重力是地球与人之间做的功。
∫A1,B1A2B2f21⋅=0dr21垂直
考虑一对力做功之和 e.g. 支持力,传送带上摩擦力。
保守力判据
∮F⋅dr=⎩⎨⎧=0=0<0F conservativeF non−conservativeF dissipative
∇=ex∂x∂+ey∂y∂+ez∂z∂:gradient operator
Stokes 公式:
∮LF⋅dr=∬(∇×F)⋅dS
质点在保守力场中的势能
引入势能
势能的引入 物体在保守力场中 a,b 两点的势能 Epa,Epb 之差等于质点由 a 点移动到 b 点过程中保守力做的功 Aab。
Epa−Epb=Aab
保守力做的功等于系统势能的减少。
引力场
EpB(−rBGmM)+EkB=EpA(−rAGmM)+EkA
总是相等的。是一个不变量。在保守力场中,质点的动能可以以“势能”的形式保存起来,也可以通过做功的方式再释放出来称为对外做功的“动能”。
AA→B=−(EpB−EpA)
势能还可以有一个常量的差别,如引力势能:
Ep=−rGmM+Const⇒E∞=0,Ep=−rGmM
重力势能 zb=0 Epb=0 Ep=mgz
引力势能 rb=∞ Epb=0 Ep=−rGMm
弹性势能 xb=0 Epb=0 Ep=21kx2
离心力的势能 Ep=−21mω2r2
Ep+mgh=0
推出
h=2gω2r2
保守力和势能的关系
积分关系
Ep(r)=∫ppoF(r)⋅dr
微分关系
dA=−dEp(r)=−dEp(x,y,z)
dA=Fxdx+Fydy+Fzdz
全微分:
dEp=∂x∂Epdx+∂y∂Epdy+∂z∂Epdz
Fx=−∂x∂EpFy=−∂y∂EpFz=−∂z∂Ep
需要对应相等。
F=−(∂x∂Epi+∂y∂Epj+∂z∂Epk)=−∇Ep
总结:
- 保守力做的功等于势能的减少;
- 保守力为势能函数的梯度负值。
势能曲线

定性分析力。
重力是常量,指向 z 轴负方向。
引力越远越小。
定性分析物体运动情况。
分析地球运动,极坐标系下。研究 vr,代表地球离太阳的距离的变化速率。因此,这样可以研究地球和太阳距离的变化情况。
守恒,拉格朗日量E=21mv2+(−rGMm)=21m(vr2+vθ2)+(−rGMm)=21m(dtdr)2+有效势能2mr2L2−rGMm(L守恒)
m2(E−veff)=(dtdr)2
dθdr=f(r)dtdr/dtdθ
补充:有心力的性质
-
有心力必为保守力。
-
有心力场中运动的质点相对于力心的角动量 L 守恒。
质点所受的力矩为
M=r×F=r×rFr=0
(叉乘的性质)
-
有心力场的质点始终在一垂直于其相对于力心的角动量的平面内运动。
r⋅L=r⋅(r×p)=p⋅(r×r)=0
(混合积的性质)
角动量定理,在 万有引力场 中,角动量守恒,也就是:
L=r×p=r×(mv)=r×(mvr+mvθ)=r×mvθ
∣L∣=∣mvθr∣
L=mvθr=mωr2⇒dtdθ=mr2L
- E<0 束缚体系
- E>0 开放体系
计算过程,首先,得出
dθdr=Lr2Emr2+2GMm2r−L2=F(r)
∫0r0F(r)dr=∫0θ0dθ
不妨将 2Em 看成 a,2GMm2 看成 b,−L2 看成 c,进行积分:
L∫0r0rar2+br+c1dr...(1)
这其实可以使用高数中学过的 倒置换,然后配合三角换元解决,结果是:
θ(r)=Lcasinh((b+2cr1)4ac−b21)
咦?怎么会出现根号里面是负数的情况……在这里卡了很久,其实提出一个 i 即可。
进一步化简,得到:
θ(r)=−iasinh((b+2cr1)4ac−b21)
cosh(θ(r))=−(b+2cr1)d−4ac+b21
r1=−2cdcosh(θ(r))−2cb
这已经是椭圆曲线的形式,为了获得其对应通式的系数,对椭圆曲线的通式做如下变形:
r=1+εcosθpr1=pεcosθ+p1
计算得到,
p=GMm2L2ε=GMm232EL2+G2M2m3=1+G2M2m32EL2
ε<1 时为椭圆,ε>1 时为双曲线,ε=1 时为抛物线,ε=0 时为圆。
对结果的粗略验证
-
当 E=0 时,ε 显然为 1,轨迹为抛物线。
-
令 ε=0,则算出
E=−2L2G2M2m3=−2m2v2R2G2M2m3=−2RGMm
恰为匀速圆周运动的总机械能。
补充的讨论
对于 (1) 式的积分,我们在计算的时候存在凑微分的过程,当凑出来判别式小于 0
∫t2+x21dx=ln(x+t2+x2)+C=asinh(tx)+C
判别式大于 0
∫t2−x21dx=arcsin(tx)+C
在以上的过程中,我们默认能量处于最低势能以上的位置。
但是当能量处于最低势能以下的位置,即 b2−4ac>0,
E<−2rGMm
两个星体就会发生撞击。在极坐标中描点作图如下。

质点系的势能
一对内力做功
多质点系统的势能
Ep=i<j∑Epij
其中 Epij 为质点 i 和 j 之间的相互作用势能。
功能原理 能量守恒定律
质点系的动能定理
设第 i 个质点所受外力的功为 Aie,内力的功为 AiI,初速度为 vi0,末速度为 vi。
CI 代表保守,NI 代表非保守。
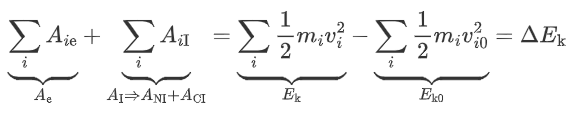
ACI=−(Ep−Ep0)=−ΔEp
Ae+ANI=(Ek+Ep)−(Ek0+Ep0)
ΔEk 代表内力和外力做功之和,引力、摩擦力之类的内力,也会改变动能。
说明
- 明确系统初末态。
- 适用于惯性系。
- 机械能守恒定律。
系统的动能和势能可以转换,当 ACI>0,势能转化为动能,当 ACI<0,动能转化为势能,各质点之间的机械能也可以互换,但保持系统的总机械能不变。
在某一惯性系中机械能守恒,但在另一惯性系中机械能不一定守恒。因为 ANI 与参照系无关,而 $A_\mathrm e $ 与参照系有关。
对于孤立系统:Ae=0,则 ANI=ΔE。能量转换和守恒定理。
- ANI<0ΔE>0 其他形式的能量转化为机械能。
- ANI<0ΔE<0 机械能转化为其他形式的能量。
对于孤立系统,系统的总能量不变。
质点系动能定理
A=i∑21mivi2−i∑21mivi02
其中 A 代表内力和外力做功之和,为什么,因为内力也有摩擦力,消耗能量。而质点系运动定律和动量定律内力都可以互相抵消,因此,不算内力。
能量不守恒的情况
摩擦力作用。速度突变。
习题
常见的解题方法:初末态,有无他力的功、正负号。
例 3-1

F3=−K(xi+yj)
相当于二维平面内的弹簧。
保守力的定义:
∮F⋅dr=0
环路积分的性质:
∮dx=0∮f(x)dx=0
对于其它轴也是如此。
例 3-2
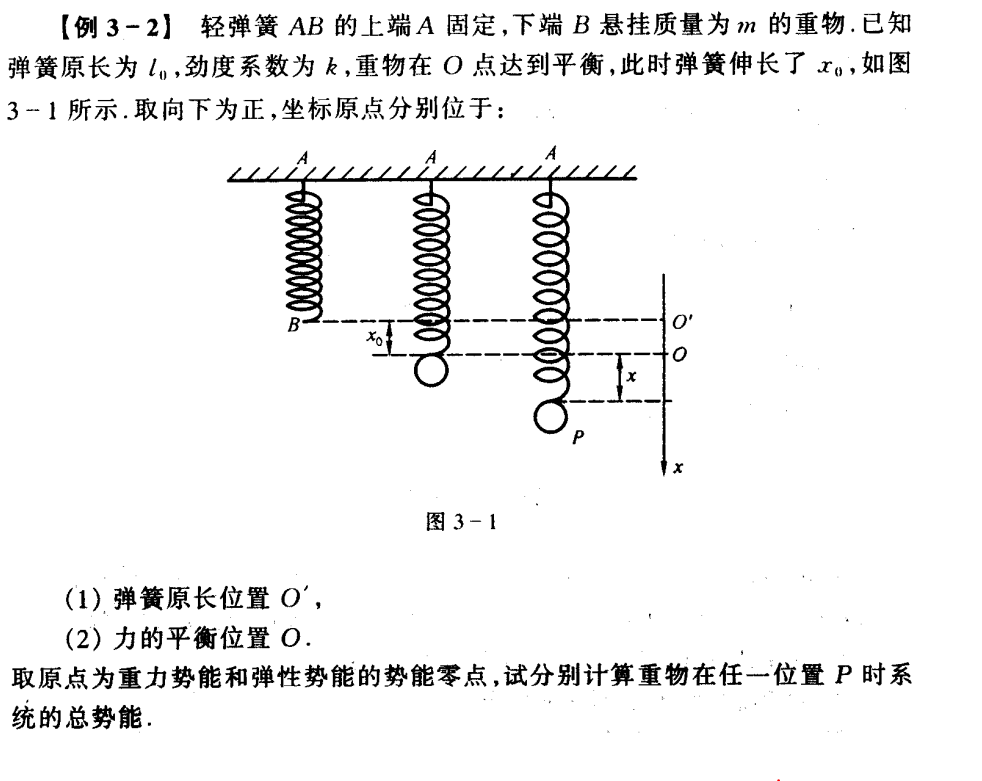
取力的平衡位置为原点,系统的总势能与只有弹性势能时是等效的,这样选取势能零点,非常方便。
例 3-3
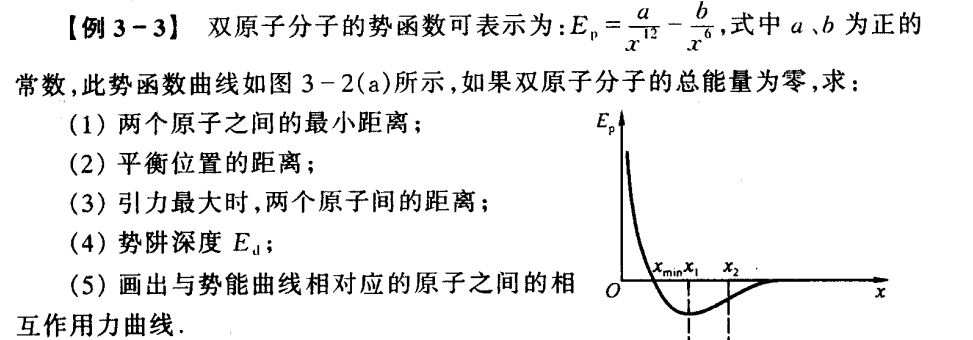

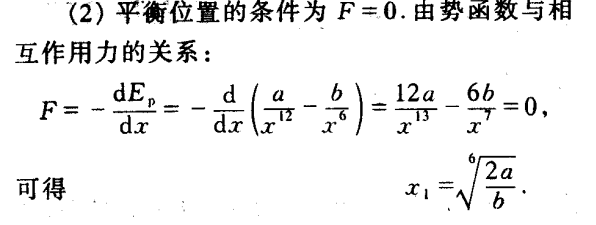
由 −dEp/dx 得到力,进一步得到力的最大值。
平衡时的位置代表势能最小,动能最大,势阱深度就是此时的势能。
例 3-4
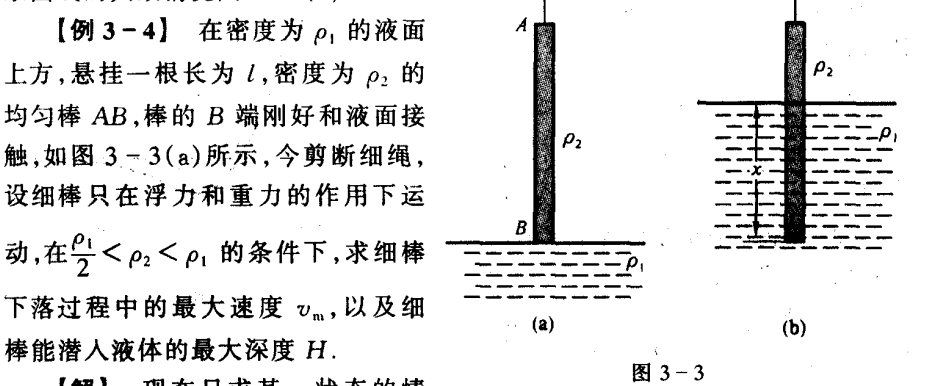
设潜入液体的深度为 h,则棒所受浮力为 Fb=ρ1ghS,其中 S 为棒的横截面。棒所受重力为 Fg=ρ2lgS。
当 Fb=Fg 时,即 h=ρ1ρ2l 时,速度最大。使用动能定理:
21(ρ2lS)vm2=ρ2lhgS−21ρ1gh2S
因此
vm=ρ1ρ2lg
对于最大深度,动能为 0,而且注意到棒全部没入液体。
ρ2lHgS−棒全部没入液体时21ρ1gl2S−排开液体的质量ρ1Sl⋅g(H−l)=0
得到
H=ρ1−ρ2ρ1⋅2l
继续的讨论,如果 ρ1/2>ρ2,则棒不会全部没入水中,会做振动。如果 ρ1<ρ2,则下沉具有向下加速度,不会有最大速度和最大深度。
例 3-5

陨落到地面:设卫星在高度为 r 的轨道总机械能是 E(r),则需要阻力做 E(R)−E(r0) 的负功。不过为了求出时间,我们需要研究经过 dt 的时间,卫星下降的高度是多少。
因此,分析 dt 时间内,阻力做的功:
dAF=−kvds=−kv2dt
在高度为 r 的轨道,卫星的总机械能为:
E(r)=−G2rm0m
因此,经过 dt 的时间,下降了多少 dr,
dAF=dE=d(−Grm0m)=G2r2m0mdrdt=−2kmrdr
积分即可得。
习题 3.1

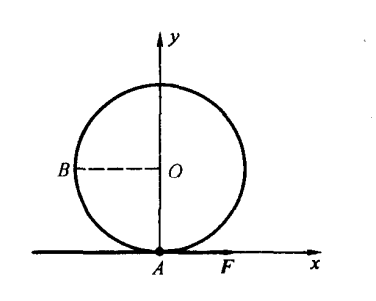
A=∫ABF⋅dr=∫AB0.6i⋅(idx+jdy)=∫AB0.6dx=−12 J
习题 3.2

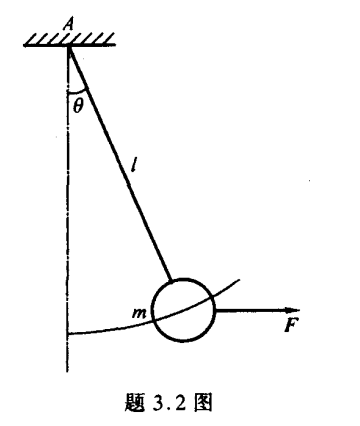
平衡状态:F=mgtanα。
可以这样计算做功:
A=∫0θFi⋅dr=∫mgtanαi⋅(lcosαdαi+lsinαdαj)=mgl∫sinαdα=mgl(1−cosθ)
计算重力所做的功。
动能不变。为 mgl(1−cosθ)。
习题 3.3

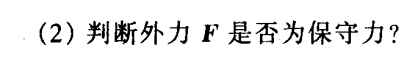
-
A=∫abraerdr=∫rarbradr=alnrarb
-
是保守力,可以写成 A=alnrb−alnra。
习题 3.4

-
−3RGmm0
-
−3RGmm0+RGmm0
习题 3.5

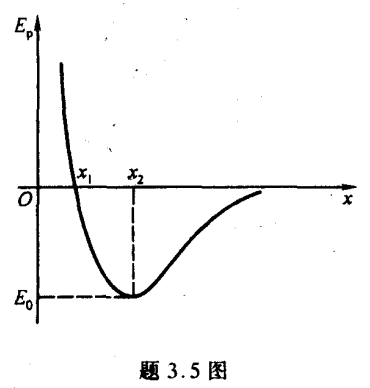
习题 3.6
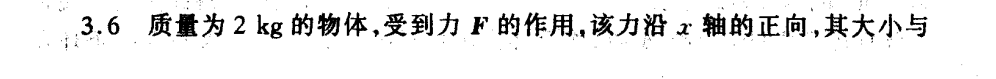

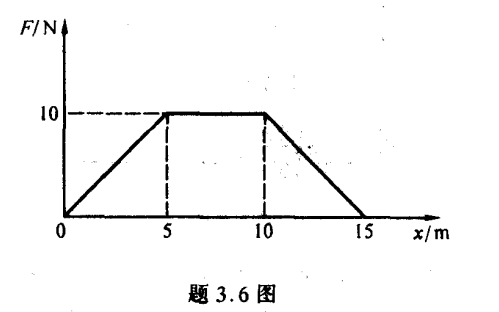
A1=∫Fdx=25 JA2=75 J
1-50