刚体力学

刚体运动的描述

刚体的定义

任何情况下形状和体积都不改变的物体（理想化的模型）刚体是特殊的质点系，其上各质元间的相对位置不改变。

自由度

完全描述运动所需的独立坐标数。

• 质点的直线运动，自由度 $=1$。
• 质点的一般运动，自由度 $=3$。
• $N$ 个质点的一般运动，自由度 $=3N$。
• 刚体，需要确定三个点。第一个点 $3$ 个自由度，第二个点间距确定，形成一个球面，两个自由度，第三个点轨迹形成一个圆，一个自由度。因此需要 $6$ 个自由度。

刚体的运动形式

• 平动 (translation) 三个自由度。
• 转动 (rotation) 定轴转动、定点转动
  • 定轴转动 运动过程中各质元均做圆周运动，中心都在一条固定的直线（转轴上）。一个自由度，选定参考方向，利用夹角 $\theta$ 即可确定刚体的位置。
  • 定点转动 转轴方向两个自由度，转轴角度一个自由度。
• 平面平行运动 分解为平动 (2)+转动 (1) 类似于平面上的陀螺。汽车里的行星齿轮。
• 一般运动 $6$ 个自由度。

处理定轴转动的物理基础：

$\boxed{\boldsymbol M=\frac{\mathrm d \boldsymbol L}{\mathrm d t}}$

刚体的定轴转动定理

刚体所受的力矩 只有垂直于转轴的外力分量才会产生沿转轴方向的力矩 $M_z$，而平行于转轴的外力分量会被抵消，为 $0$。

设第 $i$ 个质元受外力 $\boldsymbol F_i$，并且假定 $\boldsymbol F_i$ 垂直于转轴，得到刚体所受的关于定轴的合力矩：

$M_z=\sum_i M_{iz}=\sum_i r_i F_i\sin\theta_i$

刚体定轴转动的角动量

$\boldsymbol L=\sum_i \boldsymbol L_i=\sum_i(\boldsymbol R_i\times\Delta m_i\boldsymbol v_i)$

得到

$L_i=R_i\cdot \Delta m_iv_i \Rightarrow L_{iz}=L_i\sin\varphi_i=R_i\cdot \Delta m_i v_i \sin\varphi_1 =r_i \cdot \Delta m_iv_i$

对整个刚体：

$L_z=\sum_i L_{iz}=\sum_i r_i \Delta m_i v_i =\left(\sum_{i} \Delta m_i r_i^2 \right) \omega\\ J:=\sum_i \Delta m_i r_i^2 称为刚体对转轴 z 的转动惯量$

$\boxed{L_z=J\omega}$

称为刚体对转轴 $z$ 的角动量。

刚体定轴转动定律

由质点系的角动量定理，

$\boldsymbol M=\frac{\mathrm d L}{\mathrm dt}$

对刚体的定轴转动，有

$\boldsymbol M_z=\frac{\mathrm d L_z}{\mathrm d t}$

得到

$M=\frac{\mathrm d (J\omega)}{\mathrm d t} =J\frac{\mathrm d \omega}{\mathrm d t}=J\alpha$

$\boxed{\int_{t_0}^t M\mathrm d t=J\omega-J_0\omega_0}$

称为角冲量。

阿特伍德机

整体的角动量

$(m_1g-m_2g)R=\frac{\mathrm d (L_1+L_2+L_3)}{\mathrm d t}\\ =\frac{\mathrm d (m_1vR+m_2vR+J\omega)}{\mathrm d t}=m_1Ra+m_2Ra+J\underbrace{\frac{a}{R}}_{\beta}$

得到了 $a$。

当 $m_1=m_2$ ，角动量守恒。假设滑轮向 $1$ 物体的方向转动，那么

$m_2v_2+(-m_1v_1-J\omega)=0$

打击中心问题

质心运动定律分量式：

$\left\{ \begin{aligned} &F_t=F+N_x=ma_{ct}=m\left(\frac{l}{2}\alpha\right)\\ &F_n=N_y-mg=ma_{cn}=m\left(\frac{l}{2}\omega^2\right)\approx 0 \end{aligned} \right.$

而 $\alpha=M/J$，得到 $M=Fl_0,J=\frac{1}{3}ml^2$，因此

$N_x=\frac{ml}{2}\frac{Fl_0}{\frac{1}{3}ml^2}-F=\left(\frac{3l_0}{2l}-1\right)F$

当 $l_0<\frac{2}{3}l$ 时，$N_x<0$。

当 $l_0=\frac{2}{3}l$ 时，$N_x=0$。

当 $l_0>\frac{2}{3}l$，$N_x=0$。

打击中心：使得支反力为 0。如果在打击中心，可以用水平方向动量守恒。


取质元为圆环，则

$\mathrm d m=\sigma \cdot \mathrm d S=\frac{m}{\pi R^2}\cdot 2\pi r \mathrm d r$

质元所受摩擦为：

$\mathrm d f=-\mu \mathrm d mg$

那么总体摩擦力的力矩为：

$M=\int_0^R r \mathrm d f=\frac{2}{3} \mu mg R$

经过多少时间停止：因为 $M$ 是常数。

$t=\frac{M}{J}=\frac{4\mu g}{3R}$

转过的角度：

$\alpha=\omega_0/t \quad \varphi=\omega_0-\frac{1}{2}\alpha t^2=\frac{3R \omega_0^2}{8\mu g}$



刚体的转动惯量

定义

$J:=\sum_i \Delta m_i r_i^2 \quad J:=\int r^2 \mathrm d m$

其中 $r_i$ 是 $\Delta m_i$ 到转轴的垂直距离。

刚体为分立的质点组成时，用求和，为质量连续体时，用积分。

可以看出，刚体的转动惯量只和刚体本身的性质和转轴的位置有关。

均匀圆环

$\begin{aligned} J=&\int r^2 \mathrm d m\\ =&\int R^2\mathrm d m=\boxed{mR^2} \end{aligned}$

均匀圆盘

$\begin{aligned} J_c&=\int r^2\mathrm d m=\int r^2 (\underbrace{\sigma}_{面密度} \underbrace{\mathrm d S}_{增加\mathrm d r 的面积})\\ &=\int_0^R r^2 \sigma (2\pi r \mathrm d r)=\int_0^R 2\sigma \pi r^3 \mathrm d r\\ &=2\pi \sigma \frac{R^4}{4}=2\pi R^2 \sigma \frac{R^2}{2}=\frac{1}{2} mR^2 \end{aligned}$

均匀细棒绕中心

利用

$\mathrm d m=\frac{m}{l} \mathrm d x$

得到

$J=\int \underbrace{x^2}_{\mathrm d m 到转轴的垂直距离} \mathrm d m=\int_\frac{-l}{2}^\frac{l}{2} \frac{m}{l} x^2 \mathrm d x=\frac{1}{12}ml^2$

问：

1. 如果前面是 $l/3$ 后面是 $2l/3$，改变积分上下限。
2. 如果是斜着摆放，和转轴夹角为 $\theta$，改变 $r^2=x^2\sin^2\theta$。

均匀细棒绕一端

积分下限变为 $0$，积分上限为 $l$，得到

$J=\int_0^l \frac{m}{l}x^2\mathrm d x=\frac{1}{3}ml^2$

均匀球体对直径的转动惯量

分解为若干圆盘。

利用圆盘转动惯量的公式，代入

$\rho=\frac{m}{\frac{4}{3}\pi R^3}$

$J=\frac{1}{2}mR^2=\frac{1}{2}\rho VR^2$

$\mathrm d J=\frac{1}{2} \rho {\color{blue}{\pi (R\sin\theta)^2}\mathrm d z} {\color{purple}{(R\sin\theta)^2}}$

想要找到 $\mathrm d z$ 和 $\mathrm d \theta$ 的关系，得到

$z=R\cos\theta$

两边求微分，得到

$\mathrm d z=R\mathrm d (\cos\theta)$

因此，整体进行积分，得到

$J=\int \mathrm d J=\frac{1}{2}\rho\pi R^5 \int_0^\pi (\sin\theta)^4 \mathrm d (\cos\theta)=\frac{1}{2}\rho\pi R^5 \int_0^\pi (\cos^4 \theta-2\cos^2\theta+1)\mathrm d (\cos\theta)\\ =\frac{1}{2}\rho\pi R^5\left.(\frac{1}{5}t^5-\frac{2}{3}t^3+t)\right|_{-1}^1=\frac{2}{5}mR^2$

也可以使用球面坐标变换。

圆环以直径为轴

$\frac{1}{2}mR^2$

圆盘以直径为轴

$\frac{1}{4}mR^2$

平行轴定理

刚体对任一转轴的转动惯量 $J$ 等于对通过质心的平行转轴的转动惯量 $J_c$ 加上刚体质量 $m$ 乘以两平行转轴间距离 $d$ 的平方。

$\boxed{J=J_c+md^2}$

证明：

$\begin{aligned} J&=\sum_i \Delta m_i r_{io}'^2\\ &=\sum_i \Delta m_i r_{ic}^2+md^2-2\boldsymbol d\sum_{i} \Delta m_i \boldsymbol r_{ic}\\&=J_c+md^2 \end{aligned}$


垂直轴定理

垂直轴定理只适用于薄板

$J_z=\sum_i \Delta m_i r_i^2=\sum_{i}\Delta m_i(x_i^2+y_i^2)=J_y+J_x$

可以算出圆盘以直径为轴的转动惯量。


可以看为二维的棒，只不过 $x$ 轴方向拉长了。


$M=J\frac{\mathrm d \omega}{\mathrm d t}$

$mg\frac{l}{6}\cos\theta=\frac{1}{9}ml^2 \frac{\mathrm d \omega}{\mathrm d t}$

进行替换，得到

$\omega=\frac{\mathrm d \theta}{\mathrm d t} \Rightarrow \mathrm d t=\frac{\mathrm d \theta}{\omega}$

得到

$\int_0^\omega \omega\mathrm d \omega=\int_0^\frac{\pi}{2} \frac{3g}{2l}\cos\theta\mathrm d \theta$


刚体定轴转动的角动量守恒定律

$M=\frac{\mathrm d (J\omega)}{\mathrm d t}$

当 $M=0$ 时，有

$\frac{\mathrm d (J\omega)}{\mathrm d t}=0$

即 $J\omega=J_0\omega_0=\mathrm{const}$。

定轴转动角动量守恒定律：刚体在定轴转动中，当对转轴的合外力矩为零时，刚体对转轴的角动量保持不变。

适用于刚体，非刚体和物体系。

角动量守恒的情况。

1. 力过转轴。
2. 力矩均不相等，但是可以抵消。

角动量守恒的情况

1. $J,\omega$ 都不变，所以 $L=J\omega=\mathrm{const}$。
2. $J,\omega$ 都变化，但是为常数，如花样滑冰。
3. 刚体组角动量守恒。若刚体由几部分组成，且绕同一轴转动。

刚体（$J$ 不变）的角动量守恒 如直立旋转陀螺不倒。

非刚体（$J$ 可变）的角动量守恒 如芭蕾舞。

物体系的角动量守恒

若系统由几个物体组成，当系统受到的外力对轴的力矩的矢量和为零，则系统（对共同转轴）的总角动量守恒： (角动量可在刚体组内部通过内力作用传递)

$\sum_i J_i\omega_i=\mathrm{const}$

如：直升机机尾加侧向旋叶，是为防止机身的反转。


系统角动量守恒，得到

$J_0\omega_0=J\omega$

其中转动惯量

$J_0=\frac{1}{2} m_1 R^2 \quad J=J_0+m_2 (ut)^2$

得到

$\omega=\frac{\omega_0}{1+\frac{2m_2 u^2}{m_1 R^2}t^2}$

转过角度需要积分：

$\varphi=\int_0^{t_0} \omega \mathrm d t$




利用系统角动量守恒，得到

$mv_0\frac{2l}{3}=-m\frac{v_0}{2}\frac{2l}{3}+m\left(\frac{2l}{3}\right)^2\omega+2m\left(\frac{l}{3}\right)^2\omega$


$m_2 v l=\frac{1}{3}m_1 l^2 \cdot \omega -m_2 v'l$

角动量守恒，但是系统总动量不守恒。

刚体定轴转动的功能原理

刚体定轴转动的转动动能

$E_k=\sum_i \frac{1}{2} \Delta m_i v_i^2 =\frac{1}{2}\sum_i \Delta m_i r_i^2 \omega^2 =\boxed{\frac{1}{2}J\omega^2}$

由平行轴定理，可以分解为刚体绕过质心轴转动和随质心的平动。

$E_k=\frac{1}{2} J_c \omega^2 +\frac{1}{2}mv_c^2$

力矩的功

$\boxed{A=\int_{\varphi_0}^\varphi M\mathrm d \varphi}$

类似于

$A=\int_{l_0}^l F\mathrm d l$

力矩的功率

功率 $P=Fv=M\omega$。

刚体定轴转动的动能定理

$M=J\frac{\mathrm d\omega}{\mathrm d t}=J\frac{\mathrm d\omega}{\mathrm d \varphi}\frac{\mathrm d \varphi}{\mathrm d t}=J\omega\frac{\mathrm d \omega}{\mathrm d \varphi}$

刚体的重力势能

$E_p=mgz_c$

刚体定轴转动的功能原理

$\int_{\varphi_0}^\varphi M\mathrm d \varphi=(mgz_c+\frac{1}{2}J\omega^2)-(mgz_{c0}+\frac{1}{2}J\omega_0^2)$

设电风扇的功率 $P$ 恒定不变，风叶受到的空气阻力矩与风叶旋转的角速度 $\omega$ 成正比，比例系数为 $k$，并已知风叶转子的总转动惯量为 $J$，求：

1. 原来静止的电风扇通电后 $t$ 秒时刻的角速度。

   阻力矩：$-k\omega$.

   $M=J\frac{\mathrm d \omega}{\mathrm d t}=\frac{P}{\omega}-k\omega$

   得到

   $\frac{\omega \mathrm d \omega}{P-k\omega^2}=\frac{1}{J}\mathrm d t$

   也就是

   $\frac{\mathrm d(P-k\omega^2)}{P-k\omega^2}=-\frac{2k}{J} \mathrm d t$

   得到

   $\left.(\ln(P-k\omega^2))\right|_0^\omega=\left.\left(-kt/J\right)\right|_0^t$

   得到

   $\omega=\sqrt{\frac{P}{k}(1-e^{-kt/J})}$

2. 电风扇稳定转动时的角速度：

   可以令 $t \to \infin$. 得到 $\omega=\sqrt{P/k}$

   时间常数 $\tau_0=J/k$，需要到 $5\tau_0$.

均匀细棒 $m,l$，水平轴 $O$，开始棒水平，由静止释放，求：

1. 水平位置放手时，棒的质心加速度。

   重力作用于质心，得到

   $\alpha=\frac{M_z}{J}=\frac{3g}{2l}$

   $a_{ct}=\frac{l}{2}\alpha=\frac{3}{4}g \quad a_{cn}=0$

2. 摆到竖直位置时，棒的角速度。

   利用机械能守恒，得到

   $\frac{1}{2}J\omega^2-mg\frac{l}{2}=0$

   得到

   $\omega=\sqrt{\frac{3g}{l}}$

3. 摆到竖直位置时，轴的支反力。

   得到

   $a_{cn}=\frac{l}{2}\omega^2\quad F_y=mg+ma_{cn}$

弹性碰撞

$J\omega_1=J\omega_2+Lmv_B\\ \frac{1}{2}J\omega_1^2=\frac{1}{2}J\omega_2^2+\frac{1}{2}mv_B^2$

圆锥体 $R,h,J$，表面有浅槽，令 $\omega_0$ 转动，小滑块 $m$ 由静止从顶端下滑，不计摩擦，求滑到底部滑块相对于圆锥体的速度、圆锥体角速度。

对竖直轴的角动量守恒、竖直方向的角动量守恒

因为重力方向始终垂直。

$J\omega_0=(J+mR^2)\omega$

小物块的速度可以分解为相对圆锥运动和圆锥体相对地的运动

$\boldsymbol u+\boldsymbol \omega R$

然后叉乘 $\boldsymbol r$，发现 $\boldsymbol r \times \boldsymbol u=0$。

系统的机械能守恒

小物块的终速度的大小：

$\sqrt{u^2+\omega^2R^2}$

因为是垂直的。

$\frac{1}{2} J\omega_0^2+mgh=\frac{1}{2}J\omega^2+\frac{1}{2}m(u^2+\omega^2 R^2)$


1. 机械能守恒，刚开始和结束时刻总动能都为 0.

2. 令绳上的力为 $mg\sin\theta$。

   或者寻求 $v-S$ 关系，求导得到极值。

   还是利用机械能守恒，

   $mgS\sin\theta=\frac{1}{2}kS^2+\frac{1}{2}mv^2+\frac{1}{2}J\omega^2$

   利用绳和滑轮无摩擦，得到

   $\omega=v/R$

   这时物块的加速度为0，因此滑轮两侧的绳拉力一致。

回转仪 进动

刚体的旋转分为两个成分，高速自转、进动。

Rotation, Precession, Nutation.

当 $\mathrm d L // L$，$L$ 的方向不改变，当 $\mathrm d L \bot L$，该如何？

回转仪：由厚而重，形状对称的刚体绕对称轴高速自转的装置。

当 $M=0$ 时，角动量保持恒定，定向回转仪。

陀螺 设陀螺质量为 $m$，以角速度 $\omega$ 自转，力矩为

$mgr\sin\theta$

还有绕自身旋转的角动量，得到

$\mathrm d \boldsymbol L=\boldsymbol M \cdot \mathrm d t$

$\mathrm d \boldsymbol L\bot\boldsymbol L$

$\boldsymbol L$ 时刻改变方向而大小不变。

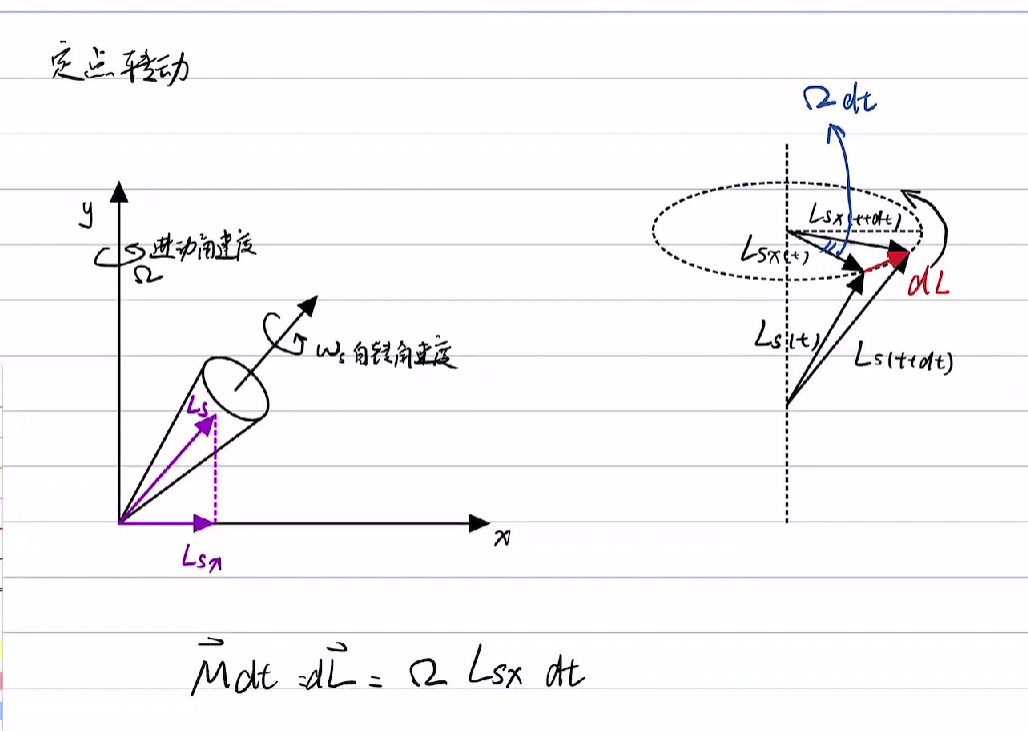
进动角速度的计算

几何关系

$|\mathrm d L|=|L|\sin\theta \cdot \mathrm d \varphi=J_c\omega \sin\theta \cdot \mathrm d \varphi$

物理规律，$\mathrm d \boldsymbol L=\boldsymbol M \cdot \mathrm d t$。

$|\mathrm d L|=|M|\cdot \mathrm d t=mgr\sin\theta \cdot \mathrm d t$

进动 Precession 角速度

$\Omega=\frac{\mathrm d \varphi}{\mathrm d t}=\frac{mgr}{J_c\omega}$

$\omega$ 越大，$\Omega$ 越小。

$\omega$ 改变方向，$L$ 朝向向下，$\Omega$ 方向相反。

一般来说，转动刚体对参考点的角动量和角速度是不平行的，但是如果刚体轴对称质量分布，那么就是平行的。

杠杆回转仪



还是推公式罢！

$\boxed{\mathrm d L=L \mathrm d \varphi=M\mathrm d t}$

$L=J_c\omega=\frac{1}{4}md^2\omega$.

$\Omega=\frac{\mathrm d \varphi}{\mathrm d t}=\frac{M}{L}=\frac{mgl}{\frac{1}{4}md^2\omega}=\frac{4gl}{d^2\omega}$

刚体的平面运动

刚体做平面运动，都可以转化为随质心平动和绕质心轴的转动。

$\boxed{\sum \boldsymbol F_i=m\boldsymbol a_c\quad \boldsymbol M_c=J_c \boldsymbol \alpha}$

分解任意质元的速度：

$\boldsymbol v_i=\boldsymbol v_c+\boldsymbol \omega \times \boldsymbol r_i$

动能也可以进行分解：

$\boxed{E_k=\frac{1}{2}mv_c^2+\frac{1}{2}J_c \omega^2}$

其中 $M=M_c +M_I$，其中 $M_I$ 是惯性力矩

$\boldsymbol M_I=\sum_i \boldsymbol r_i'\times (-\Delta m_i\boldsymbol a_c)$

然后得到 $M_I=0$。


质心运动定理：

$a_c=\frac{F}{m}$

$Fd =J_c \alpha \Rightarrow \alpha=\frac{Fd}{J_c}=\frac{12Fd}{ml^2}$



纯滚动的条件：$s=\varphi r,v=\omega r$。常规方法

$mg\sin\alpha-F_t=ma_c \quad F_N-mg\cos\alpha=0 \quad F_t r=J_c \beta$

最快求出角加速度：以接触点 $P$ 为参考点

$J_P=\frac{2}{5}mr^2+mr^2=\frac{7}{5}mr^2$

只用考虑重力的力矩：

$\beta=mg\sin\alpha \cdot r/J_P=5g\sin\alpha/7r$

推出加速度：

$a_c=r\beta$

得到时间：

$\Delta t=\sqrt{\frac{2h/\sin\alpha}{a_c}}$

然后求出速度和角速度。

能不能用机械能守恒：

$mgh+0+0=\frac{1}{2}mv^2+\frac{1}{2}J_c\omega^2\\ =\frac{1}{2}mv^2+\frac{1}{5}mr^2 \omega^2\\ =\frac{7}{10}mv^2$

因此

$v=\sqrt{\frac{10}{7}gh}\quad \omega=v/r$

连滚带滑的情况？$v\not=\omega r$。


$(\omega_0 -\Delta t\cdot \beta ) R=\Delta t \cdot a$

$\omega_0 R=\Delta t(a+\beta R)$

$\Delta t=\frac{\omega_0 R}{a+\beta R}$

$v_r=\frac{\omega_0 R}{1+\beta R/a}$

习题