二重积分的概念。引入:平面薄片的质量。
分割,分割成 Δ D i \Delta D_{i} Δ D i Δ D i \Delta D_i Δ D i Δ σ i \Delta \sigma_i Δ σ i
取值,任意取一点 ( ξ i , η i ) (\xi_i,\eta_i) ( ξ i , η i ) Δ M i ≈ ρ ( ξ i , η i ) Δ σ i \Delta M_i \approx \rho(\xi_i,\eta_i) \Delta \sigma _i Δ M i ≈ ρ ( ξ i , η i ) Δ σ i
求和,M ≈ ∑ i = 1 n ρ ( ξ i , η i ) Δ σ i M \approx \sum_{i=1}^n \rho(\xi_i,\eta_i) \Delta \sigma _i M ≈ ∑ i = 1 n ρ ( ξ i , η i ) Δ σ i
求极限,定义 d i d_i d i Δ D i \Delta D_i Δ D i
M = lim λ = max { d i } → 0 ∑ i = 1 n ρ ( ξ i , η i ) Δ σ i M=\lim_{\lambda =\max\{d_i\} \to 0}\sum_{i=1}^n \rho(\xi_i,\eta_i) \Delta \sigma _i
M = λ = max { d i } → 0 lim i = 1 ∑ n ρ ( ξ i , η i ) Δ σ i
引例二:曲顶柱体的体积。
二重积分的定义:
设 D D D f ( x , y ) f(x, y) f ( x , y ) D D D D D D Δ D 1 , Δ D 2 , ⋯ , Δ D n \Delta D_1, \Delta D_2, \cdots, \Delta D_n Δ D 1 , Δ D 2 , ⋯ , Δ D n Δ D i \Delta D_i Δ D i Δ σ i , d i \Delta \sigma_i, d_i Δ σ i , d i Δ D i \Delta D_i Δ D i ( i = 1 , 2 , ⋯ , n ) (i=1,2, \cdots, n) ( i = 1 , 2 , ⋯ , n ) Δ D i \Delta D_i Δ D i ( ξ i , η i ) ( 1 , 2 , ⋯ , n ) \left(\xi_i, \eta_i\right)(1,2, \cdots, n) ( ξ i , η i ) ( 1 , 2 , ⋯ , n ) λ = max 1 ≤ i ≤ n { d i } → 0 \lambda=\max _{1 \leq i \leq n}\left\{d_i\right\} \rightarrow 0 λ = max 1 ≤ i ≤ n { d i } → 0 ∑ i = 1 n f ( ξ i , η i ) Δ σ i \sum_{i=1}^n f\left(\xi_i, \eta_i\right) \Delta \sigma_i ∑ i = 1 n f ( ξ i , η i ) Δ σ i 确定 的极限值 I I I lim λ → 0 ∑ i = 1 n f ( ξ i , η i ) Δ σ i = I \lim _{\lambda \rightarrow 0} \sum_{i=1}^n f\left(\xi_i, \eta_i\right) \Delta \sigma_i=I lim λ → 0 ∑ i = 1 n f ( ξ i , η i ) Δ σ i = I f ( x , y ) f(x, y) f ( x , y ) D D D f ∈ R ( D ) f \in R(D) f ∈ R ( D ) I I I f ( x , y ) f(x, y) f ( x , y ) D D D
记作:
∬ D f ( x , y ) d σ \iint_D f(x,y)\mathrm d \sigma
∬ D f ( x , y ) d σ
即:
∬ D f ( x , y ) d σ = lim λ → 0 ∑ i = 1 n f ( ξ i , η i ) Δ σ i \iint_D f(x,y)\mathrm d \sigma=\lim_{\lambda \to 0}\sum_{i=1}^n f(\xi_i,\eta_i) \Delta \sigma _i
∬ D f ( x , y ) d σ = λ → 0 lim i = 1 ∑ n f ( ξ i , η i ) Δ σ i
几何意义、物理意义。特别地:
S ( D ) = ∬ D 1 d σ S(D)=\iint_D 1\mathrm d \sigma
S ( D ) = ∬ D 1 d σ
二重积分的存在性 :若函数 f ( x , y ) f(x,y) f ( x , y ) D D D f ∈ R ( D ) f \in R(D) f ∈ R ( D )
设 Ω \Omega Ω f ( x , y , z ) f(x, y, z) f ( x , y , z ) Ω \Omega Ω Ω \Omega Ω Δ Ω 1 , Δ Ω 2 , ⋯ , Δ Ω n \Delta \Omega_1, \Delta \Omega_2, \cdots, \Delta \Omega_n Δ Ω 1 , Δ Ω 2 , ⋯ , Δ Ω n Δ Ω i \Delta \Omega_i Δ Ω i ( ξ i , η i , ζ i ) \left(\xi_i, \eta_i, \zeta_i\right) ( ξ i , η i , ζ i ) Δ Ω i \Delta \Omega_i Δ Ω i Δ v i ( i = 1 , 2 , ⋯ , n ) \Delta v_i(i=1,2, \cdots, n) Δ v i ( i = 1 , 2 , ⋯ , n ) d i d_i d i Δ Ω i \Delta \Omega_i Δ Ω i λ = max 1 ≤ i ≤ n { d i } → 0 \lambda=\max _{1 \leq i \leq n}\left\{d_i\right\} \rightarrow 0 λ = max 1 ≤ i ≤ n { d i } → 0 ∑ i = 1 n f ( ξ i , η i , ζ i ) Δ v i \sum_{i=1}^n f\left(\xi_i, \eta_i, \zeta_i\right) \Delta v_i ∑ i = 1 n f ( ξ i , η i , ζ i ) Δ v i I I I lim λ → 0 ∑ i = 1 n f ( ξ i , η i , ζ i ) Δ v i = I \lim _{\lambda \rightarrow 0} \sum_{i=1}^n f\left(\xi_i, \eta_i, \zeta_i\right) \Delta v_i=I lim λ → 0 ∑ i = 1 n f ( ξ i , η i , ζ i ) Δ v i = I f ( x , y , z ) f(x, y, z) f ( x , y , z ) Ω \Omega Ω I I I f ( x , y , z ) f(x, y, z) f ( x , y , z ) Ω \Omega Ω
记作:
∭ Ω f ( x , y , z ) d V \iiint_\Omega f(x,y,z)\mathrm d V
∭ Ω f ( x , y , z ) d V
极限
lim n → + ∞ ∑ i = 1 n ∑ j = 1 n 2 π sin 2 j π n n 2 + i 2 = lim n → + ∞ 1 n ∑ i = 1 n 1 n ∑ j = 1 n 2 π sin 2 j π n 1 + ( i / n ) 2 = lim n → + ∞ 1 n ∑ i = 1 n ∫ 0 1 2 π sin 2 π w 1 + ( i / n ) 2 = lim n → + ∞ 1 n ∑ i = 1 n ∫ 0 2 π sin y 1 + ( i / n ) 2 d y = ∫ 0 1 d x ∫ 0 2 π sin y 1 + x 2 d y = ∫ 0 2 π d y ∫ 0 1 sin y 1 + x 2 d x \begin{aligned}
\lim_{n \to +\infin} \sum_{i=1}^n \sum_{j=1}^n \frac{2\pi \sin \frac{2j\pi}{n}}{n^2+i^2} &= \lim_{n \to +\infin} \frac{1}{n} \sum_{i=1}^n \frac{1}{n} \sum_{j=1}^n \frac{2\pi \sin \frac{2j\pi}{n}}{1+(i/n)^2}\\
&=\lim_{n \to +\infin} \frac{1}{n}\sum_{i=1}^n \int_{0}^1 \frac{2\pi \sin 2\pi w}{1+(i/n)^2}\\
&=\lim_{n \to +\infin} \frac{1}{n}\sum_{i=1}^n \int_{0}^{2\pi} \frac{\sin y}{1+(i/n)^2} \mathrm d y\\
&=\int_0^1 \mathrm d x \int_0^{2\pi}\frac{\sin y}{1+x^2} \mathrm d y\\
&=\int_0^{2\pi} \mathrm d y \int_0^1\frac{\sin y}{1+x^2} \mathrm d x
\end{aligned}
n → + ∞ lim i = 1 ∑ n j = 1 ∑ n n 2 + i 2 2 π sin n 2 j π = n → + ∞ lim n 1 i = 1 ∑ n n 1 j = 1 ∑ n 1 + ( i / n ) 2 2 π sin n 2 j π = n → + ∞ lim n 1 i = 1 ∑ n ∫ 0 1 1 + ( i / n ) 2 2 π sin 2 π w = n → + ∞ lim n 1 i = 1 ∑ n ∫ 0 2 π 1 + ( i / n ) 2 sin y d y = ∫ 0 1 d x ∫ 0 2 π 1 + x 2 sin y d y = ∫ 0 2 π d y ∫ 0 1 1 + x 2 sin y d x
线性性。
积分区域可加性。
保号性 ⇒ \Rightarrow ⇒
估值:若 f ∈ R ( D ) f \in R(D) f ∈ R ( D ) m ≤ f ( x , y ) ≤ M , ∀ ( x , y ) ∈ D m \le f(x,y)\le M,\forall (x,y) \in D m ≤ f ( x , y ) ≤ M , ∀ ( x , y ) ∈ D
m ⋅ S ( D ) ≤ ∬ D f ( x , y ) d σ ≤ M ⋅ S ( D ) m\cdot S(D) \le \iint_D f(x,y)\mathrm d \sigma \le M\cdot S(D)
m ⋅ S ( D ) ≤ ∬ D f ( x , y ) d σ ≤ M ⋅ S ( D )
绝对值不等式:代数和的绝对值小于等于绝对值的和。
积分中值定理:
若 f ∈ C ( D ) , g ∈ R ( D ) f \in C(D), g \in R(D) f ∈ C ( D ) , g ∈ R ( D ) g ( x , y ) g(x, y) g ( x , y ) D D D ∃ ( ξ , η ) ∈ D \exists(\xi, \eta) \in D ∃ ( ξ , η ) ∈ D
∬ D f ( x , y ) ⋅ g ( x , y ) d σ = f ( ξ , η ) ⋅ ∬ D g ( x , y ) d σ , \iint_D f(x, y) \cdot g(x, y) \mathrm{d} \sigma=f(\xi, \eta) \cdot \iint_D g(x, y) \mathrm{d} \sigma,
∬ D f ( x , y ) ⋅ g ( x , y ) d σ = f ( ξ , η ) ⋅ ∬ D g ( x , y ) d σ ,
当 g ( x , y ) = 1 g(x, y)=1 g ( x , y ) = 1 f ( ξ , η ) = ∬ D f ( x , y ) d σ S ( D ) f(\xi, \eta)=\frac{\iint_D f(x, y) \mathrm{d} \sigma}{S(D)} f ( ξ , η ) = S ( D ) ∬ D f ( x , y ) d σ f ( x , y ) f(x, y) f ( x , y ) D D D S ( D ) S(D) S ( D ) D D D
三重积分也有类似的性质。
设 a > 0 , b ( ≠ a ) > 0 a >0,b(\not=a) >0 a > 0 , b ( = a ) > 0
I 1 = ∬ x 2 + y 2 ≤ a 2 ( a 2 − x 2 − y 2 ) d σ I_1 =\iint_{x^2+y^2 \le a^2} (a^2-x^2-y^2)\mathrm d \sigma
I 1 = ∬ x 2 + y 2 ≤ a 2 ( a 2 − x 2 − y 2 ) d σ
I 2 = ∬ x 2 + y 2 ≤ b 2 ( a 2 − x 2 − y 2 ) d σ = f ( b 2 ) I_2 =\iint_{x^2+y^2 \le b^2} (a^2-x^2-y^2)\mathrm d \sigma = f(b^2)
I 2 = ∬ x 2 + y 2 ≤ b 2 ( a 2 − x 2 − y 2 ) d σ = f ( b 2 )
容易发现 f ( a 2 ) f(a^2) f ( a 2 )
画出积分区域图。
选择特殊的分割方式 d σ = d x d y \mathrm d \sigma=\mathrm d x\mathrm d y d σ = d x d y
∬ D f ( x , y ) d σ = ∬ D f ( x , y ) d x d y \iint_D f(x,y)\mathrm d \sigma =\iint_{D} f(x,y)\mathrm d x\mathrm d y
∬ D f ( x , y ) d σ = ∬ D f ( x , y ) d x d y
分片积分(二次积分),求出一个一个薄片的体积。
∫ a b d x ∫ y 1 ( x ) y 2 ( x ) f ( x , y ) d y \int_a^b \mathrm d x\int_{y_1(x)}^{y_2(x)} f(x,y)\mathrm d y
∫ a b d x ∫ y 1 ( x ) y 2 ( x ) f ( x , y ) d y
正规区域:平行于 y y y D D D X X X
D = { ( x , y ) ∣ y 1 ( x ) ≤ y ≤ y 2 ( x ) , a ≤ x ≤ b } D=\{(x,y)\mid y_1(x)\le y\le y_2(x),a\le x\le b\}
D = { ( x , y ) ∣ y 1 ( x ) ≤ y ≤ y 2 ( x ) , a ≤ x ≤ b }
Y Y Y
∫ c d d y ∫ x 1 ( y ) x 2 ( y ) f ( x , y ) d x \int_c^d \mathrm d y\int_{x_1(y)}^{x_2(y)} f(x,y)\mathrm d x
∫ c d d y ∫ x 1 ( y ) x 2 ( y ) f ( x , y ) d x
关键:积分次序 、积分上下限 ,对积分区域(非正规区域、分段函数、max , min \max,\min max , min 。
如果是绝对值,还有更加简便的方法。
X X X y y y Y Y Y x x x
积分的难易度也有区别。
计算二重积分
∬ D y 1 + x 2 − y 2 d σ \iint _D y\sqrt{1+x^2-y^2}\mathrm d \sigma
∬ D y 1 + x 2 − y 2 d σ
其中积分区域 D D D y = x , x = − 1 , y = 1 y=x,x=-1,y=1 y = x , x = − 1 , y = 1
考虑 X X X
∫ a + x d x = 1 3 ( a + x ) 3 2 + C \int \sqrt{a+x}\mathrm d x=\frac{1}{3} (a+x)^\frac{3}{2} +C
∫ a + x d x = 3 1 ( a + x ) 2 3 + C
∫ − 1 1 d x ∫ x 1 1 2 1 + x 2 − y 2 d ( y 2 ) = − ∫ − 1 1 d x 1 3 ( 1 + x 2 − y 2 ) 3 2 ∣ x 1 = − 1 3 ∫ − 1 1 ( ∣ x ∣ 3 − 1 ) d x = − 1 3 ∫ − 1 0 ( − x 3 − 1 ) d x − 1 3 ∫ 0 1 ( x 3 − 1 ) d x = 1 2 \int_{-1}^1 \mathrm d x\int_x^1 \frac{1}{2}\sqrt{1+x^2-y^2}\mathrm d (y^2)=-\left.\int_{-1}^1 \mathrm dx \frac{1}{3} {\color{red}(1+x^2-y^2)^{\frac{3}{2}}}\right|^1_x\\
=-\frac{1}{3}\int_{-1}^1 (|x|^3-1)\mathrm d x=-\frac{1}{3} \int_{-1}^0 (-x^3-1)\mathrm d x-\frac{1}{3} \int_0^1 (x^3-1)\mathrm d x\\
=\frac{1}{2}
∫ − 1 1 d x ∫ x 1 2 1 1 + x 2 − y 2 d ( y 2 ) = − ∫ − 1 1 d x 3 1 ( 1 + x 2 − y 2 ) 2 3 ∣ ∣ ∣ ∣ x 1 = − 3 1 ∫ − 1 1 ( ∣ x ∣ 3 − 1 ) d x = − 3 1 ∫ − 1 0 ( − x 3 − 1 ) d x − 3 1 ∫ 0 1 ( x 3 − 1 ) d x = 2 1
注意 ( x 2 ) 3 2 = ∣ x ∣ 3 (x^2)^\frac{3}{2}=|x|^3 ( x 2 ) 2 3 = ∣ x ∣ 3
计算二重积分 ∬ D x y d σ \displaystyle \iint_D xy \mathrm d \sigma ∬ D x y d σ D D D y 2 = x , y = x − 2 y^2=x,y=x-2 y 2 = x , y = x − 2
Y Y Y
∬ d x y d σ = ∫ − 1 2 d y ∫ y 2 y + 2 x y d x = 1 2 ∫ − 1 2 y [ ( y + 2 ) 2 − y 4 ] d y \iint_d xy \mathrm d \sigma = \int_{-1}^2 \mathrm d y \int_{y^2}^{y+2} xy \mathrm d x=\frac{1}{2}\int_{-1}^2 y [(y+2)^2-y^4] \mathrm d y
∬ d x y d σ = ∫ − 1 2 d y ∫ y 2 y + 2 x y d x = 2 1 ∫ − 1 2 y [ ( y + 2 ) 2 − y 4 ] d y
如果选择 X X X
积分区域图不好画。可以画函数图像,也可以取点。
交换二次积分的积分次序:
∫ 0 1 d x ∫ 2 x − x 2 2 − x f ( x , y ) d y \int_0^1 \mathrm d x \int_{\sqrt{2x-x^2}}^{2-x} f(x,y)\mathrm d y
∫ 0 1 d x ∫ 2 x − x 2 2 − x f ( x , y ) d y
y = 2 x − x 2 ⇒ x = 1 ± 1 − y 2 y=\sqrt{2x-x^2} \Rightarrow x=1\pm\sqrt{1-y^2} y = 2 x − x 2 ⇒ x = 1 ± 1 − y 2 x x x
∫ 0 1 d y ∫ 0 1 − 1 − y 2 f ( x , y ) d x + ∫ 1 2 d y ∫ 0 2 − y f ( x , y ) d x \int_0^1 \mathrm d y \int_0^{1-\sqrt{1-y^2}} f(x,y)\mathrm d x+\int_1^2 \mathrm d y \int_0^{2-y} f(x,y)\mathrm d x
∫ 0 1 d y ∫ 0 1 − 1 − y 2 f ( x , y ) d x + ∫ 1 2 d y ∫ 0 2 − y f ( x , y ) d x
计算二重积分
∬ D sin y y d σ \iint_D \frac{\sin y}{y}\mathrm d \sigma
∬ D y sin y d σ
其中积分区域 D D D y = x , y 2 = x y=x,y^2=x y = x , y 2 = x
先对变量 x x x
∫ 0 1 d y ∫ y 2 y sin y y d x = ∫ 0 1 ( sin y − y sin y ⏟ 分 部 积 分 ) d y = − cos y ∣ 0 1 + ( y cos y − sin y ) ∣ 0 1 = 1 − sin 1 \begin{aligned}
&\int_0^1 \mathrm{~d} y \int_{y^2}^y \frac{\sin y}{y} \mathrm{~d} x=\int_0^1(\sin y-\underbrace{y \sin y}_{分部积分}) \mathrm{d} y \\
& =-\left.\cos y\right|_0 ^1+\left.(y \cos y-\sin y)\right|_0 ^1=1-\sin 1
\end{aligned}
∫ 0 1 d y ∫ y 2 y y sin y d x = ∫ 0 1 ( sin y − 分 部 积 分 y sin y ) d y = − cos y ∣ 0 1 + ( y cos y − sin y ) ∣ 0 1 = 1 − sin 1
给你二次积分,一般都要交换次序。
【例题9】计算二次积分 ∫ 0 1 d x ∫ x 1 x 2 e − y 2 d y \displaystyle \int_0^1 \mathrm{~d} x \int_x^1 x^2 \mathrm{e}^{-y^2} \mathrm{~d} y ∫ 0 1 d x ∫ x 1 x 2 e − y 2 d y y y y = ∫ 0 1 e − y 2 d y ∫ 0 y x 2 d x = 1 3 ∫ 0 1 y 3 e − y 2 d y \displaystyle =\int_0^1 \mathrm{e}^{-y^2} \mathrm{~d} y \int_0^y x^2 \mathrm{~d} x=\frac{1}{3} \int_0^1 y^3 \mathrm{e}^{-y^2} \mathrm{~d} y = ∫ 0 1 e − y 2 d y ∫ 0 y x 2 d x = 3 1 ∫ 0 1 y 3 e − y 2 d y y 2 = t y^2=t y 2 = t
原式 = 1 6 ∫ 0 1 t e − t d t = 1 6 ( − ( t + 1 ) e − t ) ∣ 0 1 = 1 6 − 1 3 e \text { 原式 }=\frac{1}{6} \int_0^1 t \mathrm{e}^{-t} \mathrm{~d} t=\frac{1}{6}(-\left.(t+1) \mathrm{e}^{-t})|_0 ^1=\frac{1}{6}-\frac{1}{3 \mathrm{e}}\right.
原式 = 6 1 ∫ 0 1 t e − t d t = 6 1 ( − ( t + 1 ) e − t ) ∣ 0 1 = 6 1 − 3 e 1
计算二次积分
∫ 0 1 d y ∫ y 1 e y x d x \int_0^1 \mathrm d y \int_{\sqrt{y}}^1 e^\frac{y}{x}\mathrm d x
∫ 0 1 d y ∫ y 1 e x y d x
原式:
∫ 0 1 d x ∫ 0 x 2 e y x d y = ∫ 0 1 x ( e x − 1 ) d x \int_0^1 \mathrm d x\int_0^{x^2} e^\frac{y}{x}\mathrm d y=\int_0^1 x(e^x-1)\mathrm d x
∫ 0 1 d x ∫ 0 x 2 e x y d y = ∫ 0 1 x ( e x − 1 ) d x
变种 :变上限函数(积不出的),考虑 求导 ,交换积分次序 。
设 f ( x ) = ∫ 0 a − x e y ( 2 a − y ) d y \displaystyle f(x)=\int_0^{a-x} e^{y(2a-y)} \mathrm d y f ( x ) = ∫ 0 a − x e y ( 2 a − y ) d y ∫ 0 a f ( x ) d x \displaystyle \int_0^a f(x)\mathrm d x ∫ 0 a f ( x ) d x
原式
∫ 0 a e y ( 2 a − y ) d y ∫ 0 a − y d x = ∫ 0 a ( a − y ) e a 2 − ( a − y ) 2 d y = 1 2 ( e a 2 − 1 ) \int_0^a e^{y(2a-y)}\mathrm d y \int_0^{a-y}\mathrm d x=\int_{0}^a (a-y) e^{a^2-(a-y)^2}\mathrm d y=\frac{1}{2} (e^{a^2}-1)
∫ 0 a e y ( 2 a − y ) d y ∫ 0 a − y d x = ∫ 0 a ( a − y ) e a 2 − ( a − y ) 2 d y = 2 1 ( e a 2 − 1 )
若 y ( x ) = ∫ 0 x arctan ( u − 1 ) 2 d u \displaystyle y(x)=\int_0^x \arctan (u-1)^2 \mathrm d u y ( x ) = ∫ 0 x arctan ( u − 1 ) 2 d u ∫ 0 1 y ( x ) d x \displaystyle \int_0^1 y(x)\mathrm d x ∫ 0 1 y ( x ) d x
变上限函数求导 亦可以做。
∫ 0 1 y ( x ) d x = x y ( x ) ∣ 0 1 − ∫ 0 1 x y ′ ( x ) d x = ∫ 0 1 arctan ( u − 1 ) 2 d u − ∫ 0 1 x arctan ( x − 1 ) 2 d x = ⋯ \int_0^1 y(x)\mathrm d x=xy(x)|^1_0-\int_0^1 xy'(x)\mathrm d x=\int_0^1 \arctan(u-1)^2\mathrm d u-\int_0^1 x\arctan (x-1)^2 \mathrm d x= \cdots
∫ 0 1 y ( x ) d x = x y ( x ) ∣ 0 1 − ∫ 0 1 x y ′ ( x ) d x = ∫ 0 1 arctan ( u − 1 ) 2 d u − ∫ 0 1 x arctan ( x − 1 ) 2 d x = ⋯
注意:积分的合并。
设 f ( x ) f(x) f ( x ) F ( t ) = ∫ 1 t d y ∫ y t f ( x ) d x \displaystyle F(t)=\int_1^t \mathrm d y \int_y^t f(x)\mathrm d x F ( t ) = ∫ 1 t d y ∫ y t f ( x ) d x F ′ ( 2 ) F'(2) F ′ ( 2 )
回忆变上限函数的求导,如果形式如
d ( ∫ ψ ( t ) φ ( t ) f ( t ) d t ) / d t \mathrm d \left(\int_{\psi(t)}^{\varphi(t)} f(t) \mathrm dt \right)/\mathrm dt
d ( ∫ ψ ( t ) φ ( t ) f ( t ) d t ) / d t
就要想尽方法把 t t t f ( t ) f(t) f ( t )
在这里,我们交换积分的上下限,使得积分的结构改变。
计算二重积分
∬ D max { x y , 1 } d σ \iint_D \max \{xy,1\}\mathrm d \sigma
∬ D max { x y , 1 } d σ
D 1 = { ( x , y ) ∣ 0 ≤ x ≤ 2 , 0 ≤ y ≤ 2 } D_1=\{(x,y)|0 \le x \le 2 ,0 \le y \le 2\}
D 1 = { ( x , y ) ∣ 0 ≤ x ≤ 2 , 0 ≤ y ≤ 2 }
D 2 = { ( x , y ) ∣ x y ≥ 1 , x ≥ 0 , y ≥ 0 } D_2=\{(x,y)|xy \ge 1 , x\ge 0,y \ge 0\}
D 2 = { ( x , y ) ∣ x y ≥ 1 , x ≥ 0 , y ≥ 0 }
D 1 D_1 D 1
原式
4 − ∬ D 2 1 d σ + ∬ D 2 x y d σ 4-\iint_{D_2} 1\mathrm d \sigma + \iint_{D_2} xy \mathrm d \sigma
4 − ∬ D 2 1 d σ + ∬ D 2 x y d σ
计算二重积分
∬ D ∣ y − x 2 ∣ d σ \iint_D \sqrt{|y-x^2|}\mathrm d \sigma
∬ D ∣ y − x 2 ∣ d σ
其中 D = { ( x , y ) ∣ − 1 ≤ x ≤ 1 , 0 ≤ y ≤ 2 } D=\{(x,y)|-1 \le x \le 1,0 \le y \le2\} D = { ( x , y ) ∣ − 1 ≤ x ≤ 1 , 0 ≤ y ≤ 2 }
还是分割两部分 D 1 , D 2 D_1,D_2 D 1 , D 2
原式
∬ D 1 x 2 − y d σ + ∬ D 2 y − x 2 d σ \iint_{D_1} \sqrt{x^2-y}\mathrm d \sigma +\iint_{D_2} \sqrt{y-x^2}\mathrm d \sigma
∬ D 1 x 2 − y d σ + ∬ D 2 y − x 2 d σ
还是先对 y y y x 2 x^2 x 2
出现了
∫ − 1 1 ( 2 − x 2 ) 3 2 d x \int_{-1}^1 (2-x^2)^\frac{3}{2}\mathrm d x
∫ − 1 1 ( 2 − x 2 ) 2 3 d x
三角代换 令 x = 2 sin t x=\sqrt{2} \sin t x = 2 sin t
∬ D y ∣ x − y 2 ∣ d x d y \iint_D y \sqrt{|x -y^2|} \mathrm d x \mathrm d y
∬ D y ∣ x − y 2 ∣ d x d y
其中 D = { ( x , y ) ∣ 0 ≤ x ≤ 4 , 0 ≤ y ≤ 1 } D=\{(x,y) \mid 0 \le x \le 4 ,0 \le y \le 1\} D = { ( x , y ) ∣ 0 ≤ x ≤ 4 , 0 ≤ y ≤ 1 }
设 f ( x ) f(x) f ( x ) g ( x ) g(x) g ( x ) R \R R K ( x , y ) K(x,y) K ( x , y ) R 2 \R^2 R 2
∫ 0 1 f ( y ) K ( x , y ) d y = g ( x ) ∫ 0 1 g ( y ) K ( x , y ) d y = f ( x ) \int_0^1 f(y)K(x,y)\mathrm d y=g(x) \quad \int_0^1 g(y)K(x,y)\mathrm d y=f(x)
∫ 0 1 f ( y ) K ( x , y ) d y = g ( x ) ∫ 0 1 g ( y ) K ( x , y ) d y = f ( x )
若
m = min x ∈ [ 0 , 1 ] f ( x ) g ( x ) , M = max x ∈ [ 0 , 1 ] f ( x ) g ( x ) m=\min_{x\in[0,1]} \frac{f(x)}{g(x)},M=\max_{x\in[0,1]}\frac{f(x)}{g(x)}
m = x ∈ [ 0 , 1 ] min g ( x ) f ( x ) , M = x ∈ [ 0 , 1 ] max g ( x ) f ( x )
则 m M = 1 mM=1 m M = 1
做出变换
g ( x ) = ∫ 0 1 f ( y ) g ( y ) ⋅ g ( y ) K ( x , y ) d y g(x)=\int_0^1 \frac{f(y)}{g(y)} \cdot g(y)K(x,y)\mathrm d y
g ( x ) = ∫ 0 1 g ( y ) f ( y ) ⋅ g ( y ) K ( x , y ) d y
进而
m f ( x ) = ∫ 0 1 m g ( y ) K ( x , y ) d y ≤ ∫ 0 1 f ( y ) g ( y ) ⋅ g ( y ) K ( x , y ) d y ⏟ g ( x ) ≤ ∫ 0 1 M g ( y ) K ( x , y ) d y = M f ( x ) mf(x)=\int_0^1 m g(y)K(x,y)\mathrm d y\le\int_0^1 \underbrace{\frac{f(y)}{g(y)}\cdot g(y)K(x,y)\mathrm d y}_{g(x)} \le \int_0^1 Mg(y)K(x,y)\mathrm d y=Mf(x)
m f ( x ) = ∫ 0 1 m g ( y ) K ( x , y ) d y ≤ ∫ 0 1 g ( x ) g ( y ) f ( y ) ⋅ g ( y ) K ( x , y ) d y ≤ ∫ 0 1 M g ( y ) K ( x , y ) d y = M f ( x )
因此
m ≤ g ( x ) f ( x ) = 1 M M ≤ g ( x ) f ( x ) = 1 m m \le \frac{g(x)}{f(x)}=\frac{1}{M} \quad M\le\frac{g(x)}{f(x)}=\frac{1}{m}
m ≤ f ( x ) g ( x ) = M 1 M ≤ f ( x ) g ( x ) = m 1
因此 m M = 1 mM=1 m M = 1
使用卷积,得到
f ( x ) = ∫ 0 1 g ( y ) K ( x , y ) d y f(x)=\int_0^1 g(y) K(x,y) \mathrm d y
f ( x ) = ∫ 0 1 g ( y ) K ( x , y ) d y
也就是
f ( t ) = ∫ 0 1 g ( y ) K ( t , y ) d y f(t)=\int_0^1 g(y)K(t,y) \mathrm d y
f ( t ) = ∫ 0 1 g ( y ) K ( t , y ) d y
代入 g ( x ) g(x) g ( x )
g ( x ) = ∫ 0 1 f ( t ) K ( x , t ) d t = ∫ 0 1 ∫ 0 1 g ( y ) K ( t , y ) d y K ( x , t ) d t = ∫ 0 1 g ( y ) ∫ 0 1 K ( x , t ) K ( t , y ) d t d y g(x)=\int_0^1 f(t) K(x,t) \mathrm d t=\int_0^1\int_0^1 g(y)K(t,y) \mathrm d y \, K(x,t) \mathrm d t=\int_0^1 g(y) \int_0^1 K(x,t)K(t,y) \mathrm dt \, \mathrm d y
g ( x ) = ∫ 0 1 f ( t ) K ( x , t ) d t = ∫ 0 1 ∫ 0 1 g ( y ) K ( t , y ) d y K ( x , t ) d t = ∫ 0 1 g ( y ) ∫ 0 1 K ( x , t ) K ( t , y ) d t d y
令 L ( x , y ) = ∫ 0 1 K ( x , t ) K ( t , y ) d t \displaystyle L(x,y)=\int_0^1 K(x,t)K(t,y)\mathrm d t L ( x , y ) = ∫ 0 1 K ( x , t ) K ( t , y ) d t L ( x , y ) L(x,y) L ( x , y )
因此,
g ( x ) = ∫ 0 1 g ( y ) L ( x , y ) d y g(x)=\int_0^1 g(y)L(x,y) \mathrm d y
g ( x ) = ∫ 0 1 g ( y ) L ( x , y ) d y
两侧同除 g ( x ) g(x) g ( x )
∫ 0 1 g ( y ) g ( x ) L ( x , y ) d y = 1 \int_0^1 \frac{g(y)}{g(x)} L(x,y) \mathrm d y=1
∫ 0 1 g ( x ) g ( y ) L ( x , y ) d y = 1
同理,对于 f ( x ) f(x) f ( x )
∫ 0 1 f ( y ) f ( x ) L ( x , y ) d y = 1 \int_0^1 \frac{f(y)}{f(x)} L(x,y) \mathrm d y=1
∫ 0 1 f ( x ) f ( y ) L ( x , y ) d y = 1
两者作差,得到
∫ 0 1 ( g ( y ) g ( x ) − f ( y ) f ( x ) ) L ( x , y ) d y = 0 \int_0^1 \left(\frac{g(y)}{g(x)} -\frac{f(y)}{f(x)}\right) L(x,y) \mathrm d y=0
∫ 0 1 ( g ( x ) g ( y ) − f ( x ) f ( y ) ) L ( x , y ) d y = 0
由于积分中值定理,得到 ∃ y 0 ∈ [ 0 , 1 ] \exists y_0 \in[0,1] ∃ y 0 ∈ [ 0 , 1 ]
g ( y 0 ) g ( x ) − f ( y 0 ) f ( x ) = 0 \frac{g(y_0)}{g(x)}-\frac{f(y_0)}{f(x)}=0
g ( x ) g ( y 0 ) − f ( x ) f ( y 0 ) = 0
因此,∀ x ∈ [ 0 , 1 ] \forall x \in[0,1] ∀ x ∈ [ 0 , 1 ]
f ( x ) g ( x ) = f ( y 0 ) g ( y 0 ) = m = M \frac{f(x)}{g(x)}=\frac{f(y_0)}{g(y_0)}=m=M
g ( x ) f ( x ) = g ( y 0 ) f ( y 0 ) = m = M
得到 m = M = 1 m=M=1 m = M = 1 f ( x ) = g ( x ) f(x)=g(x) f ( x ) = g ( x )
当二重积分存在时,在极坐标系,可用由原点发出的射线和半径为常数的同心圆来划分积分区域 D D D
小矩形的长 r d θ r \mathrm d \theta r d θ d r \mathrm d r d r
二重积分的积分元素为 d σ = r d r d θ \mathrm d \sigma =r \mathrm d r \mathrm d \theta d σ = r d r d θ
“凭空”多了一个 r r r
∬ D f ( x , y ) d σ = ∬ D f ( r cos θ , r sin θ ) ⋅ r d r d θ \iint _D f(x,y) \mathrm d \sigma = \iint _D f(r \cos \theta, r\sin \theta) \cdot {\color{red}{r \mathrm d r \mathrm d \theta}}
∬ D f ( x , y ) d σ = ∬ D f ( r cos θ , r sin θ ) ⋅ r d r d θ
需要转化为极坐标形式 $f(r, \theta) $。
注意,积分元素为 d σ = d x d y = r d r d θ \mathrm d \sigma=\mathrm d x\mathrm d y={\color{blue}r\mathrm d r} {\color{green}\mathrm d\theta} d σ = d x d y = r d r d θ
θ \theta θ
D = { ( r , θ ) ∣ r 1 ( θ ) ≤ r ≤ r 2 ( θ ) , α ≤ θ ≤ β } D=\{(r,\theta) \mid r_1 (\theta) \le r \le r_2 (\theta),\alpha \le \theta \le \beta\}
D = { ( r , θ ) ∣ r 1 ( θ ) ≤ r ≤ r 2 ( θ ) , α ≤ θ ≤ β }
∫ α β d θ ∫ r 1 ( θ ) r 2 ( θ ) f ( r cos θ , r sin θ ) ⋅ r d r \int_\alpha^\beta {\color{green}\mathrm d \theta} \int_{r_1 (\theta)}^{r_2 (\theta)} f(r \cos \theta,r\sin\theta) \cdot {\color{blue}{r \mathrm d r}}
∫ α β d θ ∫ r 1 ( θ ) r 2 ( θ ) f ( r cos θ , r sin θ ) ⋅ r d r
θ \theta θ r r r
积分区域内含有原点,要求 r ( θ ) r(\theta) r ( θ )
∫ 0 2 π d θ ∫ 0 r ( θ ) f ( r cos θ , r sin θ ) ⋅ r d r \int_0^{2\pi} {\color{green}\mathrm d \theta} \int_{0}^{r (\theta)} f(r \cos \theta,r\sin\theta) \cdot {\color{blue}{r \mathrm d r}}
∫ 0 2 π d θ ∫ 0 r ( θ ) f ( r cos θ , r sin θ ) ⋅ r d r
如果是奇函数,还可以从 − π -\pi − π π \pi π
极坐标变换中点火公式用的比较多:
∫ 0 π 2 sin n x d x = ( m − 1 ) ! ! m ! ! m o d d ∫ 0 π 2 sin n x d x = ( m − 1 ) ! ! m ! ! π 2 m e v e n \int_0^\frac{\pi}{2} \sin^n x \mathrm d x =\frac{(m-1)!!}{m!!} ~m\mathrm{~odd}\quad \int_0^\frac{\pi}{2} \sin^n x \mathrm d x =\frac{(m-1)!!}{m!!}\frac{\pi}{2} ~m\mathrm{~even}
∫ 0 2 π sin n x d x = m ! ! ( m − 1 ) ! ! m o d d ∫ 0 2 π sin n x d x = m ! ! ( m − 1 ) ! ! 2 π m e v e n
r r r
使用较少。
D = { ( r , θ ) ∣ θ 1 ( r ) ≤ θ ≤ θ 2 ( r ) , a ≤ θ ≤ b } D=\{(r,\theta) \mid \theta_1 (r) \le \theta \le \theta_2 (r),a \le \theta \le b\}
D = { ( r , θ ) ∣ θ 1 ( r ) ≤ θ ≤ θ 2 ( r ) , a ≤ θ ≤ b }
则二重积分:
∫ a b r d r ∫ θ 1 ( r ) θ 2 ( r ) f ( r cos θ , r sin θ ) ⋅ d θ \int_a^b {\color{blue}{r \mathrm d r}} \int_{\theta_1 (r)}^{\theta_2 (r)} f(r \cos \theta,r\sin\theta) \cdot{\color{green}\mathrm d \theta}
∫ a b r d r ∫ θ 1 ( r ) θ 2 ( r ) f ( r cos θ , r sin θ ) ⋅ d θ
r r r θ \theta θ
设 a > 0 a>0 a > 0 ∬ D f ( x , y ) d σ \displaystyle \iint_D f(x,y)\mathrm d \sigma ∬ D f ( x , y ) d σ D D D
满足 x ≥ 0 , y ≥ 0 , x 2 + y 2 ≤ a 2 x \ge0,y \ge 0,x^2+y^2 \le a^2 x ≥ 0 , y ≥ 0 , x 2 + y 2 ≤ a 2 x 2 + y 2 ≥ a x x^2+y^2\ge ax x 2 + y 2 ≥ a x
化为 r 2 ≥ a r cos θ r^2 \ge ar\cos \theta r 2 ≥ a r cos θ r ≥ a cos θ r \ge a\cos \theta r ≥ a cos θ r ≤ a r \le a r ≤ a
∫ 0 π / 2 d θ ∫ a cos θ a f ( r cos θ , r sin θ ) ⋅ r d r \int_0^{\pi/2} {\color{green}\mathrm d \theta} \int_{a\cos \theta}^{a} f(r \cos \theta,r\sin\theta) \cdot {\color{blue}{r \mathrm d r}}
∫ 0 π / 2 d θ ∫ a cos θ a f ( r cos θ , r sin θ ) ⋅ r d r
满足 x ≥ 0 , y ≥ 0 , x 2 + y 2 ≤ a 2 x\ge 0,y \ge 0,x^2+y^2 \le a^2 x ≥ 0 , y ≥ 0 , x 2 + y 2 ≤ a 2 ( x 2 + y 2 ) 2 ≥ a 2 ( x 2 − y 2 ) (x^2+y^2)^2 \ge a^2(x^2-y^2) ( x 2 + y 2 ) 2 ≥ a 2 ( x 2 − y 2 )
属于 r 4 ≥ a 2 r 2 cos 2 θ r^4 \ge a^2 r^2 \cos 2 \theta r 4 ≥ a 2 r 2 cos 2 θ r 2 ≥ a 2 cos 2 θ r^2 \ge a^2 \cos 2\theta r 2 ≥ a 2 cos 2 θ 双纽线 。
看到双纽线,要想到切线 π / 4 \pi/4 π / 4
∫ 0 π 4 d θ ∫ a 2 cos 2 θ a f ( r cos θ , r sin θ ) ⋅ r d r + ∫ π 4 π 2 d θ ∫ 0 a f ( r cos θ , r sin θ ) ⋅ r d r \int_{0}^{\frac{\pi}{4}} \mathrm d \theta \int_{a\sqrt{2 \cos 2\theta}}^a f(r\cos\theta,r\sin\theta)\cdot r \mathrm d r+\int_{\frac{\pi}{4}}^\frac{\pi}{2} \mathrm d \theta \int_0^a f(r\cos\theta,r\sin\theta)\cdot r \mathrm d r
∫ 0 4 π d θ ∫ a 2 cos 2 θ a f ( r cos θ , r sin θ ) ⋅ r d r + ∫ 4 π 2 π d θ ∫ 0 a f ( r cos θ , r sin θ ) ⋅ r d r
曲线 ( x 2 + y 2 ) 2 = 2 a 2 ( x 2 − y 2 ) (x^2+y^2)^2=2a^2(x^2-y^2) ( x 2 + y 2 ) 2 = 2 a 2 ( x 2 − y 2 )
是双纽线,因此只需要计算 − π 4 ≤ θ ≤ π 4 -\frac{\pi}{4} \le \theta \le \frac{\pi}{4} − 4 π ≤ θ ≤ 4 π
补充内容
常见的极坐标曲线。
直线 x + y = 2 x+y=2 x + y = 2
r = 2 cos θ + sin θ ( − π 4 < θ < 3 π 4 ) r=\frac{2}{\cos \theta+\sin \theta} \left(-\frac{\pi}{4} < \theta < \frac{3 \pi}{4}\right)
r = cos θ + sin θ 2 ( − 4 π < θ < 4 3 π )
如果要求这种积分,可以极坐标转笛卡尔坐标 。
心脏线 r = a ( 1 − cos θ ) r=a(1-\cos \theta) r = a ( 1 − cos θ )
双纽线 r 2 = a 2 cos 2 θ , ( x 2 + y 2 ) 2 = a 2 ( x 2 − y 2 ) r^2=a^2 \cos 2 \theta,(x^2+y^2)^2 = a^2(x^2-y^2) r 2 = a 2 cos 2 θ , ( x 2 + y 2 ) 2 = a 2 ( x 2 − y 2 ) 默认 r ≥ 0 r \ge 0 r ≥ 0
双叶玫瑰线 r = a cos 2 θ r=a \cos 2\theta r = a cos 2 θ
三叶玫瑰线 r = a cos 3 θ r=a \cos 3\theta r = a cos 3 θ
计算二重积分 ∬ D e − x 2 − y 2 d σ \iint_D e^{-x^2-y^2}\mathrm d \sigma ∬ D e − x 2 − y 2 d σ x x x y y y
D = { ( x , y ) ∣ x 2 + y 2 ≤ a 2 ( a > 0 ) } D=\{(x,y)\mid x^2+y^2 \le a^2 (a>0)\}
D = { ( x , y ) ∣ x 2 + y 2 ≤ a 2 ( a > 0 ) }
交换积分坐标 。
利用极坐标计算。
∫ 0 2 π d θ ∫ 0 a e − r 2 ⋅ r d r = π ( 1 − e − a 2 ) \int_0^{2\pi}\mathrm d \theta \int_0^a e^{-r^2} \cdot r \mathrm d r = \pi (1-e^{-a^2})
∫ 0 2 π d θ ∫ 0 a e − r 2 ⋅ r d r = π ( 1 − e − a 2 )
看到积分区域是圆,或者很多平方,根号之类的,就要使用极坐标。
x 2 + ( y − a ) 2 = a 2 ⇒ r = 2 a sin θ x^2+(y-a)^2=a^2 \Rightarrow r=2a\sin\theta
x 2 + ( y − a ) 2 = a 2 ⇒ r = 2 a sin θ
计算二重积分
∬ D R 2 − x 2 − y 2 d σ \iint_D \sqrt{R^2-x^2-y^2}\mathrm d \sigma
∬ D R 2 − x 2 − y 2 d σ
其中 D = { ( x , y ) ∣ x 2 + y 2 ≤ R x ( R > 0 ) } D=\{(x,y) \mid x^2+y^2 \le Rx (R >0)\} D = { ( x , y ) ∣ x 2 + y 2 ≤ R x ( R > 0 ) }
将二重积分
∬ D f ( x , y ) d σ \iint_D f(x,y)\mathrm d \sigma
∬ D f ( x , y ) d σ
其中 D = { ( x , y ) ∣ a 2 ≤ x 2 + y 2 ≤ b 2 } D=\{(x,y)\mid a^2 \le x^2+y^2 \le b^2\} D = { ( x , y ) ∣ a 2 ≤ x 2 + y 2 ≤ b 2 }
化为
∫ 0 2 π d θ ∫ a b f ( r cos θ , r sin θ ) ⋅ r d r \int_0^{2\pi} \mathrm d \theta \int_a^b f(r\cos \theta,r \sin \theta)\cdot r\mathrm d r
∫ 0 2 π d θ ∫ a b f ( r cos θ , r sin θ ) ⋅ r d r
∫ a b r d r ∫ 0 2 π f ( r cos θ , r sin θ ) ⋅ d θ \int_a^b r\mathrm d r \int_0^{2\pi} f(r\cos \theta,r \sin \theta)\cdot \mathrm d \theta
∫ a b r d r ∫ 0 2 π f ( r cos θ , r sin θ ) ⋅ d θ
不能直接计算第一象限的四倍。可以用大圆上的积分减去小圆上的积分?需要整个大圆内都有意义。
计算二重积分
∬ D x + y x 2 + y 2 d σ \iint_D \frac{x+y}{x^2+y^2} \mathrm d \sigma
∬ D x 2 + y 2 x + y d σ
其中
D = { ( x , y ) ∣ x 2 + y 2 ≤ 1 , x + y ≥ 1 } D=\{(x,y)\mid x^2+y^2 \le 1,x+y \ge 1\}
D = { ( x , y ) ∣ x 2 + y 2 ≤ 1 , x + y ≥ 1 }
x + y = 1 ⇔ r cos θ + r sin θ = 1 ⇒ r = 1 cos θ + sin θ x+y=1 \Leftrightarrow r \cos \theta+r \sin \theta=1 \Rightarrow r = \frac{1}{\cos \theta+\sin\theta}
x + y = 1 ⇔ r cos θ + r sin θ = 1 ⇒ r = cos θ + sin θ 1
∫ 0 π 2 d θ ∫ 1 cos θ + sin θ 1 r cos θ + r sin θ r 2 ⋅ r d r = ∫ 0 π 2 ( 1 − 1 cos θ + sin θ ) ( cos θ + sin θ ) d θ = ( sin θ − cos θ − θ ) ∣ 0 π 2 = 2 − π 2 \int_0^\frac{\pi}{2} \mathrm d \theta\int_\frac{1}{\cos \theta + \sin \theta}^1 \frac{r\cos \theta + r\sin \theta}{r^2} \cdot r \mathrm d r\\=\int_0^\frac{\pi}{2} \left(1-\frac{1}{\cos \theta+\sin \theta}\right) (\cos \theta+\sin \theta) \mathrm d \theta=(\sin \theta-\cos \theta-\theta) | _{0}^\frac{\pi}{2}=2-\frac{\pi}{2}
∫ 0 2 π d θ ∫ cos θ + sin θ 1 1 r 2 r cos θ + r sin θ ⋅ r d r = ∫ 0 2 π ( 1 − cos θ + sin θ 1 ) ( cos θ + sin θ ) d θ = ( sin θ − cos θ − θ ) ∣ 0 2 π = 2 − 2 π
计算二重积分
∬ D ∣ x − y ∣ d x d y \iint_D |x-y|\mathrm d x \mathrm d y
∬ D ∣ x − y ∣ d x d y
其中 D = { ( x , y ) ∣ x 2 + y 2 ≤ 1 , x ≥ 0 , y ≥ 0 } D=\{(x,y)\mid x^2+y^2 \le 1 , x\ge 0,y \ge 0\} D = { ( x , y ) ∣ x 2 + y 2 ≤ 1 , x ≥ 0 , y ≥ 0 }
不是椎体,所以不能用椎体体积公式进行计算。积分区域是一个 1 / 4 1/4 1 / 4
∫ 0 π 2 d θ ∫ 0 1 r 2 ∣ cos θ − sin θ ∣ d r = 2 3 ( 2 − 1 ) \int_0^\frac{\pi}{2} \mathrm d \theta \int_0^1 r^2|\cos \theta - \sin \theta| \mathrm d r=\frac{2}{3}(\sqrt{2}-1)
∫ 0 2 π d θ ∫ 0 1 r 2 ∣ cos θ − sin θ ∣ d r = 3 2 ( 2 − 1 )
利用二重积分求平面区域
D = { ( r cos θ , r sin θ ) ∣ 1 2 ≤ r ≤ cos θ } D=\{(r\cos \theta,r\sin \theta) \mid \frac{1}{2} \le r \le \cos \theta \}
D = { ( r cos θ , r sin θ ) ∣ 2 1 ≤ r ≤ cos θ }
的面积。
还是先画出积分区域图,目的是为了确定自变量的取值,和选择哪个变量先积分。
若积分区域 D D D y y y
且 f ( x , y ) f(x,y) f ( x , y ) x x x y y y
∬ D f ( x , y ) d σ = 2 ∬ D 1 f ( x , y ) d σ \iint_D f(x,y)\mathrm d \sigma = 2\iint_{D_1} f(x,y)\mathrm d \sigma
∬ D f ( x , y ) d σ = 2 ∬ D 1 f ( x , y ) d σ
计算二重积分
∬ D x [ 1 + y f ( x 2 + y 2 ) ] d σ \iint_D x[1+y f(x^2+y^2)]\mathrm d\sigma
∬ D x [ 1 + y f ( x 2 + y 2 ) ] d σ
其中 f ( u ) f(u) f ( u ) D D D y = x 3 y=x^3 y = x 3 y = 1 , x = − 1 y=1,x=-1 y = 1 , x = − 1
用曲线 y = − x 3 y=-x^3 y = − x 3 D 1 D_1 D 1 x x x D 2 D_2 D 2 y y y
原式:
∬ D 1 x d σ = ∫ − 1 0 x d x ∫ x 3 − x 3 d y = − 2 ∫ − 1 0 x 4 d x = − 2 5 \iint_{D_1}x\mathrm d \sigma=\int_{-1}^0 x \mathrm d x \int_{x^3}^{-x^3} \mathrm d y = -2 \int_{-1}^0 x^4 \mathrm d x=-\frac{2}{5}
∬ D 1 x d σ = ∫ − 1 0 x d x ∫ x 3 − x 3 d y = − 2 ∫ − 1 0 x 4 d x = − 5 2
定理,设变换
T : { x = x ( u , v ) y = y ( u , v ) T: \left\{\begin{matrix}x=x(u,v)\\y=y(u,v)\end{matrix}\right.
T : { x = x ( u , v ) y = y ( u , v )
将 u v uv u v D 1 D_1 D 1 x y xy x y D D D
{ x ( u , v ) , y ( u , v ) ∈ C 1 ( D 1 ) J = ∂ ( x , y ) ∂ ( u , v ) ≠ 0 , ( u , v ) ∈ D 1 f ( x , y ) ∈ C ( D ) \left\{
\begin{aligned}
&x(u,v),y(u,v) \in C^1 (D_1)\\
&J=\frac{\partial(x,y)}{\partial(u,v)}\not=0,(u,v)\in D_1\\
&f(x,y)\in C(D)
\end{aligned}
\right.
⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ x ( u , v ) , y ( u , v ) ∈ C 1 ( D 1 ) J = ∂ ( u , v ) ∂ ( x , y ) = 0 , ( u , v ) ∈ D 1 f ( x , y ) ∈ C ( D )
则有:
∬ D f ( x , y ) d σ = ∬ D 1 f [ x ( u , v ) , y ( u , v ) ] ⋅ ∣ J ∣ ⋅ d u d v \iint_D f(x,y)\mathrm d \sigma=\iint_{D_1} f[x(u,v),y(u,v)] \cdot |J|\cdot \mathrm d u \mathrm d v
∬ D f ( x , y ) d σ = ∬ D 1 f [ x ( u , v ) , y ( u , v ) ] ⋅ ∣ J ∣ ⋅ d u d v
相当于
d x d y = ∂ ( x , y ) ∂ ( u , v ) ⋅ d u d v \mathrm d x\mathrm d y=\frac{\partial(x,y)}{\partial(u,v)}\cdot \mathrm d u\mathrm dv
d x d y = ∂ ( u , v ) ∂ ( x , y ) ⋅ d u d v
逆变换:
T − 1 : { u = u ( x , y ) v = v ( x , y ) T^{-1}: \left\{\begin{aligned}u=u(x,y)\\v=v(x,y)\end{aligned}\right.
T − 1 : { u = u ( x , y ) v = v ( x , y )
满足
∂ ( x , y ) ∂ ( u , v ) ⋅ ∂ ( u , v ) ∂ ( x , y ) = 1 \frac{\partial(x,y)}{\partial(u,v)} \cdot \frac{\partial(u,v)}{\partial(x,y)}=1
∂ ( u , v ) ∂ ( x , y ) ⋅ ∂ ( x , y ) ∂ ( u , v ) = 1
对于 极坐标 ,变换 T : x = r cos θ , y = r sin θ T : x=r\cos \theta,y=r \sin\theta T : x = r cos θ , y = r sin θ
J = ∂ ( x , y ) ∂ ( r , θ ) = ∣ x r x θ y r y θ ∣ = ∣ cos θ − r sin θ sin θ r cos θ ∣ = r J=\frac{\partial (x,y)}{\partial (r,\theta)}=\begin{vmatrix}x_r & x_\theta \\y_r & y_\theta\end{vmatrix}=\begin{vmatrix}\cos \theta & -r \sin\theta \\\sin \theta & r \cos \theta\end{vmatrix}=r
J = ∂ ( r , θ ) ∂ ( x , y ) = ∣ ∣ ∣ ∣ x r y r x θ y θ ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ cos θ sin θ − r sin θ r cos θ ∣ ∣ ∣ ∣ = r
因此:
∬ D f ( x , y ) d σ = ∬ D f ( r cos θ , r sin θ ) ⋅ r d r d θ \iint _D f(x,y) \mathrm d \sigma = \iint _D f(r \cos \theta, r\sin \theta) \cdot {\color{red}{r \mathrm d r \mathrm d \theta}}
∬ D f ( x , y ) d σ = ∬ D f ( r cos θ , r sin θ ) ⋅ r d r d θ
广义极坐标 :变换 T : x = a r cos θ , y = b r sin θ T:x=ar\cos \theta,y=br \sin\theta T : x = a r cos θ , y = b r sin θ
J = ∂ ( x , y ) ∂ ( r , θ ) = a b r J=\frac{\partial (x,y)}{\partial (r,\theta)}=abr
J = ∂ ( r , θ ) ∂ ( x , y ) = a b r
放缩变换 :变换 T : x = a u , y = b v T:x=au,y=bv T : x = a u , y = b v
J = a b J=ab
J = a b
计算二重积分
∬ D x y d σ \iint_D xy \mathrm d \sigma
∬ D x y d σ
其中 D D D x y = 1 , x y = 2 , y = x xy=1,xy=2,y=x x y = 1 , x y = 2 , y = x y = 4 x y=4x y = 4 x
作变量代换 T : u = x y , v = y x T:u=xy,v=\frac{y}{x} T : u = x y , v = x y D D D u v uv u v D 1 D_1 D 1
D 1 = { ( u , v ) ∣ ∣ 1 ≤ u ≤ 2 , 1 ≤ v ≤ 4 } D_1=\{(u,v)|\mid 1 \le u \le 2,1 \le v \le 4\}
D 1 = { ( u , v ) ∣ ∣ 1 ≤ u ≤ 2 , 1 ≤ v ≤ 4 }
则
x = u / v , y = u v x=\sqrt{u/v},y=\sqrt{uv}
x = u / v , y = u v
可以这样计算
J = ∂ ( x , y ) ∂ ( u , v ) J=\frac{\partial(x,y)}{\partial(u,v)}
J = ∂ ( u , v ) ∂ ( x , y )
也可以通过倒数计算
J = 1 ∂ ( u , v ) ∂ ( x , y ) = x 2 y = 1 2 v J=\frac{1}{\frac{\partial (u,v)}{\partial (x,y)}}=\frac{x}{2y}=\frac{1}{2v}
J = ∂ ( x , y ) ∂ ( u , v ) 1 = 2 y x = 2 v 1
故
∬ D x y d x d y = ∬ D 1 u ⋅ 1 2 v d u d v = 3 2 ln 2 \iint_D xy \mathrm d x\mathrm d y=\iint_{D_1} u \cdot \frac{1}{2v}\mathrm d u\mathrm d v=\frac{3}{2}\ln2
∬ D x y d x d y = ∬ D 1 u ⋅ 2 v 1 d u d v = 2 3 ln 2
求由椭圆柱体 x 2 / a 2 + y 2 / b 2 = 1 x^2/a^2+y^2/b^2=1 x 2 / a 2 + y 2 / b 2 = 1 z = 0 z=0 z = 0 z = x 2 / p 2 + y 2 / q 2 z=x^2/p^2+y^2/q^2 z = x 2 / p 2 + y 2 / q 2
所求体积为
V = ∬ D ( x 2 p 2 + y 2 q 2 ) d x d y V=\iint_D \left(\frac{x^2}{p^2}+\frac{y^2}{q^2}\right)\mathrm dx\mathrm d y
V = ∬ D ( p 2 x 2 + q 2 y 2 ) d x d y
其中 D = { ( x , y ) ∣ x 2 a 2 + y 2 b 2 ≤ 1 } D=\{(x,y)\mid \frac{x^2}{a^2}+\frac{y^2}{b^2}\le 1\} D = { ( x , y ) ∣ a 2 x 2 + b 2 y 2 ≤ 1 }
T : x = a r cos θ , y = b r sin θ T:x=ar\cos \theta,y=br \sin\theta
T : x = a r cos θ , y = b r sin θ
则
d x d y = a b r ⋅ d r d θ \mathrm d x\mathrm d y = abr\cdot \mathrm d r\mathrm d \theta
d x d y = a b r ⋅ d r d θ
D 1 = { ( r , θ ) ∣ 0 ≤ θ ≤ 2 π , 0 ≤ r ≤ 1 } D_1=\{(r,\theta)\mid 0 \le \theta \le 2\pi,0 \le r \le 1\}
D 1 = { ( r , θ ) ∣ 0 ≤ θ ≤ 2 π , 0 ≤ r ≤ 1 }
V = ∬ D ( x 2 p 2 + y 2 q 2 ) d x d y = ∫ 0 2 π d θ ∫ 0 1 ( a 2 r 2 cos 2 θ p 2 + b 2 r 2 sin 2 θ q 2 ) ⋅ a b r d r = 1 4 a b ⋅ 4 ⋅ ∫ 0 π 2 ( a 2 cos 2 θ p 2 + b 2 sin 2 θ q 2 ) d θ = a b ( a 2 p 2 ⋅ 1 2 ⋅ π 2 + b 2 q 2 ⋅ 1 2 ⋅ π 2 ) = π a b 4 ( a 2 p 2 + b 2 q 2 ) 。 \begin{aligned}
V & =\iint_D\left(\frac{x^2}{p^2}+\frac{y^2}{q^2}\right) \mathrm{d} x \mathrm{~d} y \\
& =\int_0^{2 \pi} \mathrm{d} \theta \int_0^1\left(\frac{a^2 r^2 \cos ^2 \theta}{p^2}+\frac{b^2 r^2 \sin ^2 \theta}{q^2}\right) \cdot a b r d r \\
& =\frac{1}{4} a b \cdot 4 \cdot \int_0^{\frac{\pi}{2}}\left(\frac{a^2 \cos ^2 \theta}{p^2}+\frac{b^2 \sin ^2 \theta}{q^2}\right) \mathrm{d} \theta \\
& =a b\left(\frac{a^2}{p^2} \cdot \frac{1}{2} \cdot \frac{\pi}{2}+\frac{b^2}{q^2} \cdot \frac{1}{2} \cdot \frac{\pi}{2}\right)=\frac{\pi a b}{4}\left(\frac{a^2}{p^2}+\frac{b^2}{q^2}\right) 。
\end{aligned}
V = ∬ D ( p 2 x 2 + q 2 y 2 ) d x d y = ∫ 0 2 π d θ ∫ 0 1 ( p 2 a 2 r 2 cos 2 θ + q 2 b 2 r 2 sin 2 θ ) ⋅ a b r d r = 4 1 a b ⋅ 4 ⋅ ∫ 0 2 π ( p 2 a 2 cos 2 θ + q 2 b 2 sin 2 θ ) d θ = a b ( p 2 a 2 ⋅ 2 1 ⋅ 2 π + q 2 b 2 ⋅ 2 1 ⋅ 2 π ) = 4 π a b ( p 2 a 2 + q 2 b 2 ) 。
交换 积分变量 ,积分坐标 ,进行 变量代换 。
计算
\int_0^\frac{\sqrt 2}{2} \mathrm d y\int_y ^\sqrt{1-y^2} xy e ^\frac{x^2-y^2}{\sqrt{x^2+y^2}}\mathrm d x
画出积分区域图,就发现应该使用 极坐标代换 。
1 2 ∫ 0 π 4 d θ ∫ 0 1 r 3 sin 2 θ ⋅ e r cos 2 θ ⏟ 需 要 三 次 分 部 积 分 ⋅ d r \frac{1}{2}\int_0^\frac{\pi}{4} \mathrm d \theta \int_0^1 \underbrace{r^3 \sin 2\theta \cdot e^{r \cos 2 \theta}}_{需要三次分部积分} \cdot \mathrm d r
2 1 ∫ 0 4 π d θ ∫ 0 1 需 要 三 次 分 部 积 分 r 3 sin 2 θ ⋅ e r cos 2 θ ⋅ d r
整理得到
1 2 ∫ 0 1 r 3 d r ∫ 0 π 4 sin 2 θ ⋅ e r cos 2 θ ⋅ d θ \frac{1}{2} \int_0^1 r^3 \mathrm d r \int_0^\frac{\pi}{4} \sin 2\theta \cdot e ^{r \cos 2\theta} \cdot \mathrm d \theta
2 1 ∫ 0 1 r 3 d r ∫ 0 4 π sin 2 θ ⋅ e r cos 2 θ ⋅ d θ
设函数 f ( x ) f(x) f ( x ) [ 0 , 1 ] [0,1] [ 0 , 1 ]
∫ 0 1 d x ∫ x 1 f ( x ) f ( y ) d y = 1 2 ( ∫ 0 1 f ( x ) d x ) 2 \int_0^1 \mathrm d x \int_x^1 f(x)f(y)\mathrm d y = \frac{1}{2} \left(\int_0^1\ f(x)\mathrm d x \right)^2
∫ 0 1 d x ∫ x 1 f ( x ) f ( y ) d y = 2 1 ( ∫ 0 1 f ( x ) d x ) 2
法 1
先证明
∫ 0 a d x ∫ x a f ( x ) f ( y ) d y = ∫ 0 a d x ∫ 0 x f ( y ) f ( x ) d y = 1 2 ( ∫ 0 a f ( x ) d x ) 2 \int_0^a \mathrm d x \int_x^a f(x)f(y)\mathrm d y =\int_0^a \mathrm d x \int_0^x f(y)f(x)\mathrm d y= \frac{1}{2} \left(\int_0^a\ f(x)\mathrm d x \right)^2
∫ 0 a d x ∫ x a f ( x ) f ( y ) d y = ∫ 0 a d x ∫ 0 x f ( y ) f ( x ) d y = 2 1 ( ∫ 0 a f ( x ) d x ) 2
两边对 a a a
∫ 0 a f ( a ) f ( y ) d y = f ( a ) ∫ 0 a f ( x ) d x \int_0^a f(a)f(y)\mathrm d y=f(a)\int_0^a f(x)\mathrm d x
∫ 0 a f ( a ) f ( y ) d y = f ( a ) ∫ 0 a f ( x ) d x
显然成立。
再令 a = 0 a=0 a = 0
法 2
先交换积分次序
I 1 = ∬ D 1 f ( x ) f ( y ) d x d y I_1= \iint_{D_1} f(x)f(y)\mathrm d x\mathrm d y
I 1 = ∬ D 1 f ( x ) f ( y ) d x d y
∫ 0 1 d x ∫ 0 x f ( y ) f ( x ) d y = I 2 = ∬ D 2 f ( x ) f ( y ) d x d y \int_0^1 \mathrm d x \int_0^x f(y)f(x)\mathrm d y=I_2= \iint_{D_2} f(x)f(y)\mathrm d x\mathrm d y
∫ 0 1 d x ∫ 0 x f ( y ) f ( x ) d y = I 2 = ∬ D 2 f ( x ) f ( y ) d x d y
因此加起来变成
1 2 ∫ 0 1 f ( y ) d y ∫ 0 1 f ( x ) d x = 1 2 ( ∫ 0 1 f ( x ) d x ) 2 \frac{1}{2} \int_0^1 f(y)\mathrm d y \int_0^1 f(x)\mathrm d x=\frac{1}{2} \left(\int_0^1\ f(x)\mathrm d x \right)^2
2 1 ∫ 0 1 f ( y ) d y ∫ 0 1 f ( x ) d x = 2 1 ( ∫ 0 1 f ( x ) d x ) 2
设函数 f ( x ) , g ( x ) f(x),g(x) f ( x ) , g ( x ) [ a , b ] [a,b] [ a , b ]
∫ a b f ( x ) d x ⋅ ∫ a b g ( x ) d x ≤ ( b − a ) ∫ a b f ( x ) g ( x ) d x \int_a^b f(x)\mathrm d x \cdot \int_a^b g(x)\mathrm d x \le (b-a) \int_a^b f(x)g(x)\mathrm d x
∫ a b f ( x ) d x ⋅ ∫ a b g ( x ) d x ≤ ( b − a ) ∫ a b f ( x ) g ( x ) d x
记:
I 1 = ∫ a b f ( x ) d x ⋅ ∫ a b g ( x ) d x = ∫ a b f ( x ) d x ⋅ ∫ a b g ( y ) d y = ∬ D f ( x ) g ( y ) d x d y \begin{aligned}
I_1 & =\int_a^b f(x) \mathrm{d} x \cdot \int_a^b g(x) \mathrm{d} x=\int_a^b f(x) \mathrm{d} x \cdot \int_a^b g(y) \mathrm{d} y \\
& =\iint_D f(x) g(y) \mathrm{d} x \mathrm{~d} y
\end{aligned}
I 1 = ∫ a b f ( x ) d x ⋅ ∫ a b g ( x ) d x = ∫ a b f ( x ) d x ⋅ ∫ a b g ( y ) d y = ∬ D f ( x ) g ( y ) d x d y
其中 D = { ( x , y ) ∣ a ≤ x ≤ b , a ≤ y ≤ b } D=\{(x, y) \mid a \leq x \leq b, a \leq y \leq b\} D = { ( x , y ) ∣ a ≤ x ≤ b , a ≤ y ≤ b }
I 2 = ( b − a ) ∫ a b f ( x ) g ( x ) d x = ∫ a b 1 d y ⋅ ∫ a b f ( x ) g ( x ) d x = ∬ D f ( x ) g ( x ) d x d y \begin{aligned}
I_2 & =(b-a) \int_a^b f(x) g(x) \mathrm{d} x=\int_a^b 1 \mathrm{~d} y \cdot \int_a^b f(x) g(x) \mathrm{d} x \\
& =\iint_D f(x) g(x) \mathrm{d} x \mathrm{~d} y
\end{aligned}
I 2 = ( b − a ) ∫ a b f ( x ) g ( x ) d x = ∫ a b 1 d y ⋅ ∫ a b f ( x ) g ( x ) d x = ∬ D f ( x ) g ( x ) d x d y
所以
I 2 − I 1 = ∬ D f ( x ) [ g ( x ) − g ( y ) ] d x d y I_2-I_1=\iint_D f(x)[g(x)-g(y)] \mathrm{d} x \mathrm{~d} y
I 2 − I 1 = ∬ D f ( x ) [ g ( x ) − g ( y ) ] d x d y
交换积分变量
I 2 − I 1 = ∬ D f ( y ) [ g ( y ) − g ( x ) ] d x d y I_2-I_1 = \iint_D f(y) [g(y)-g(x)]\mathrm d x\mathrm d y
I 2 − I 1 = ∬ D f ( y ) [ g ( y ) − g ( x ) ] d x d y
所以
I 2 − I 1 = 1 2 ∬ D [ f ( x ) − f ( y ) ] [ g ( x ) − g ( y ) ] ⏟ 符 号 相 同 d x d y ≥ 0 I_2-I_1 =\frac{1}{2} \iint_D \underbrace{[f(x)-f(y)][g(x)-g(y)]}_{符号相同}\mathrm d x\mathrm d y \ge 0
I 2 − I 1 = 2 1 ∬ D 符 号 相 同 [ f ( x ) − f ( y ) ] [ g ( x ) − g ( y ) ] d x d y ≥ 0
设函数 f ( x ) f(x) f ( x ) [ 0 , 1 ] [0,1] [ 0 , 1 ]
2 ∬ D t f ( x + y ) d x d y = ∬ D t f ( x ) d x d y 2 \iint_{D_t} f(x+y)\mathrm d x\mathrm d y=\iint_{D_t} f(x)\mathrm d x\mathrm d y
2 ∬ D t f ( x + y ) d x d y = ∬ D t f ( x ) d x d y
其中
D t = { ( x , y ) ∣ 0 ≤ y ≤ t − x , 0 ≤ x ≤ t } ( 0 ≤ t ≤ 1 ) D_t=\{(x,y) \mid 0 \le y \le t-x ,0 \le x \le t \}(0\le t \le 1)
D t = { ( x , y ) ∣ 0 ≤ y ≤ t − x , 0 ≤ x ≤ t } ( 0 ≤ t ≤ 1 )
证明:
t ∫ 0 t f ( x ) d x = 3 ∫ 0 t x f ( x ) d x t\int_0^t f(x)\mathrm d x = 3 \int_0^t x f(x)\mathrm d x
t ∫ 0 t f ( x ) d x = 3 ∫ 0 t x f ( x ) d x
并求出 f ( 0 ) f(0) f ( 0 )
首先,进行积分坐标的交换:
∬ D t f ( x ) d x d y = ∫ 0 t d x ∫ 0 t − x f ( x ) d y = ∫ 0 t d y ∫ 0 t − y f ( x ) d x = ∫ 0 t ( t − x ) f ( x ) d x = t ∫ 0 t f ( x ) d x − ∫ 0 t x f ( x ) d x \iint_{D_t} f(x)\mathrm d x\mathrm d y=\boxed{\int_0^t \mathrm d x \int_0^{t-x} f(x)\mathrm d y}=\int_0^t \mathrm d y \int_0^{t-y} f(x)\mathrm d x=\int_0^t (t-x) f (x)\mathrm d x=\boxed{t\int_0^t f(x)\mathrm d x-\int_0^t xf(x)\mathrm d x}
∬ D t f ( x ) d x d y = ∫ 0 t d x ∫ 0 t − x f ( x ) d y = ∫ 0 t d y ∫ 0 t − y f ( x ) d x = ∫ 0 t ( t − x ) f ( x ) d x = t ∫ 0 t f ( x ) d x − ∫ 0 t x f ( x ) d x
2 ∬ D t f ( x + y ) d x d y = 2 ∫ 0 t d x ∫ 0 t − x f ( x + y ) d y = 2 ∫ 0 t d y ∫ 0 t − y f ( x + y ) d x 2\iint_{D_t} f(x+y)\mathrm d x\mathrm d y=2\int_0^t \mathrm d x \int_0^{t-x} f(x+y)\mathrm d y=2\int_0^t \mathrm d y \int_0^{t-y} f(x+y)\mathrm d x
2 ∬ D t f ( x + y ) d x d y = 2 ∫ 0 t d x ∫ 0 t − x f ( x + y ) d y = 2 ∫ 0 t d y ∫ 0 t − y f ( x + y ) d x
需要证明
∬ D t f ( x + y ) d x d y = ∫ 0 t x f ( x ) d x \iint_{D_t} f(x+y)\mathrm d x\mathrm d y = \int_0^t xf(x)\mathrm d x
∬ D t f ( x + y ) d x d y = ∫ 0 t x f ( x ) d x
因此,需要换元,令 u = x , v = x + y u=x,v=x+y u = x , v = x + y D t = { ( u , v ) ∣ u ≤ v ≤ t , 0 ≤ u ≤ t } ( 0 ≤ t ≤ 1 ) D_t=\{(u,v) \mid u \le v \le t ,0 \le u \le t \}(0\le t \le 1) D t = { ( u , v ) ∣ u ≤ v ≤ t , 0 ≤ u ≤ t } ( 0 ≤ t ≤ 1 )
∬ D t f ( x + y ) d x d y = ∬ D t f ( v ) ∂ ( x , y ) ∂ ( u , v ) d u d v = ∫ 0 t d v ∫ 0 v f ( v ) d u = ∫ 0 t v f ( v ) d v = ∫ 0 t x f ( x ) d x \iint_{D_t} f(x+y)\mathrm d x\mathrm d y= \iint_{D_t} f(v) \frac{\partial (x,y)}{\partial(u,v)}\mathrm d u\mathrm d v=\int_0^t \mathrm d v \int_0^v f(v)\mathrm d u=\int_0^t vf(v)\mathrm d v=\int_0^t x f(x)\mathrm d x
∬ D t f ( x + y ) d x d y = ∬ D t f ( v ) ∂ ( u , v ) ∂ ( x , y ) d u d v = ∫ 0 t d v ∫ 0 v f ( v ) d u = ∫ 0 t v f ( v ) d v = ∫ 0 t x f ( x ) d x
因此得证。
下面求出 f ( 0 ) f(0) f ( 0 ) ,利用 t ∫ 0 t f ( x ) d x = 3 ∫ 0 t x f ( x ) d x \displaystyle t\int_0^t f(x)\mathrm d x = 3 \int_0^t x f(x)\mathrm d x t ∫ 0 t f ( x ) d x = 3 ∫ 0 t x f ( x ) d x
对 t t t
∫ 0 t f ( x ) d x + t f ( t ) = 3 t f ( t ) \int_0^t f(x)\mathrm d x+t\ f(t)=3t\ f(t)
∫ 0 t f ( x ) d x + t f ( t ) = 3 t f ( t )
因此,
∫ 0 t f ( x ) d x = 2 t f ( t ) \int_0^t f(x)\mathrm d x=2t\ f(t)
∫ 0 t f ( x ) d x = 2 t f ( t )
得到
∫ 0 t f ( x ) d x 2 t = f ( t ) \frac{\int_0^t f(x)\mathrm d x}{2t}=f(t)
2 t ∫ 0 t f ( x ) d x = f ( t )
lim t → 0 f ( t ) = lim t → 0 ∫ 0 t f ( x ) d x 2 t = lim t → 0 f ( t ) 2 = f ( 0 ) 2 \lim_{t\to 0} f(t)=\lim_{t \to 0}\frac{\int_0^t f(x)\mathrm d x}{2t}=\lim_{t \to 0}\frac{f(t)}{2}=\frac{f(0)}{2}
t → 0 lim f ( t ) = t → 0 lim 2 t ∫ 0 t f ( x ) d x = t → 0 lim 2 f ( t ) = 2 f ( 0 )
因此,f ( 0 ) = 0 f(0)=0 f ( 0 ) = 0
三重积分的计算步骤:
确定积分区域。
确定坐标系(坐标转换)和剖分方法,根据积分区域和被积函数确定。
d x d y d z = ∣ ∂ ( x , y , z ) ∂ ( u , v , w ) ∣ d u d v d w \displaystyle \mathrm d x\mathrm d y\mathrm d z=\left|\frac{\partial (x,y,z)}{\partial(u,v,w)}\right|\mathrm d u\mathrm d v\mathrm d w d x d y d z = ∣ ∣ ∣ ∣ ∂ ( u , v , w ) ∂ ( x , y , z ) ∣ ∣ ∣ ∣ d u d v d w 柱面坐标:{ x = r cos θ y = r sin θ z = z \left\{\begin{aligned}&x=r\cos\theta\\&y=r\sin\theta \\&z=z\end{aligned}\right. ⎩ ⎪ ⎨ ⎪ ⎧ x = r cos θ y = r sin θ z = z d x d y d z = r d r d θ d z \mathrm d x\mathrm d y\mathrm d z=r \mathrm d r\mathrm d \theta\mathrm d z d x d y d z = r d r d θ d z
球面坐标:{ x = ρ sin φ cos θ y = ρ sin φ sin θ z = ρ cos φ \left\{
\begin{aligned}
&x=\rho\sin\varphi\cos \theta\\
&y=\rho\sin\varphi\sin\theta\\
&z=\rho\cos \varphi
\end{aligned}
\right. ⎩ ⎪ ⎨ ⎪ ⎧ x = ρ sin φ cos θ y = ρ sin φ sin θ z = ρ cos φ d x d y d z = ρ 2 sin φ d ρ d θ d φ \mathrm d x\mathrm d y\mathrm d z=\rho^2 \sin\varphi\mathrm d \rho\mathrm d \theta\mathrm d \varphi d x d y d z = ρ 2 sin φ d ρ d θ d φ
直接计算。
∭ Ω f ( x , y , z ) d V \iiint_\Omega f(x,y,z)\mathrm d V
∭ Ω f ( x , y , z ) d V
回顾二重积分的计算,对于二重积分主要有两种计算方法:
利用直角坐标和极坐标计算积分。
基本思想是动点要走遍积分区域 D D D
三重积分动点如何走遍 Ω \Omega Ω
主要利用三种坐标形式。
直角坐标的积分元素,类似于二重积分有 d V = d x d y d z \mathrm d V=\mathrm d x\mathrm d y\mathrm d z d V = d x d y d z
∭ Ω f ( x , y , z ) d V = ∭ Ω f ( x , y , z ) d x d y d z \iiint_\Omega f(x,y,z)\mathrm d V=\iiint_{\Omega} f(x,y,z)\mathrm d x\mathrm d y\mathrm d z
∭ Ω f ( x , y , z ) d V = ∭ Ω f ( x , y , z ) d x d y d z
直角坐标下介绍两种方法化三重积分为三次积分。
柱线法 先定积分再二重积分。先一后二。
对于 正规区域 ,设 两部分曲面 Σ 1 , Σ 2 \Sigma_1,\Sigma_2 Σ 1 , Σ 2
z = z 1 ( x , y ) , z = z 2 ( x , y ) z=z_1(x,y),z=z_2(x,y)
z = z 1 ( x , y ) , z = z 2 ( x , y )
函数 z 1 ( x , y ) , z 2 ( x , y ) z_1(x,y),z_2(x,y) z 1 ( x , y ) , z 2 ( x , y ) D x y D_{xy} D x y z 1 ( x , y ) ≤ z 2 ( x , y ) , ( x , y ) ∈ D x y z_1(x,y)\le z_2(x,y),(x,y)\in D_{xy} z 1 ( x , y ) ≤ z 2 ( x , y ) , ( x , y ) ∈ D x y
∭ Ω f ( x , y , z ) d V = ∬ D x y d x d y ∫ z 1 ( x , y ) z 2 ( x , y ) f ( x , y , z ) d z \iiint_{\Omega} f(x,y,z)\mathrm d V=\iint_{D_{xy}} \mathrm d x\mathrm d y \int_{z_1(x,y)}^{z_2(x,y)} f(x,y,z)\mathrm d z
∭ Ω f ( x , y , z ) d V = ∬ D x y d x d y ∫ z 1 ( x , y ) z 2 ( x , y ) f ( x , y , z ) d z
对变量 z z z x , y x,y x , y D x y D_{xy} D x y
截面法 对变量 z z z z = z z=z z = z Ω \Omega Ω D z D_z D z D z D_z D z x , y x,y x , y z z z
∭ Ω f ( x , y , z ) d V = ∫ c d d z ∬ D z f ( x , y , z ) d x d y \iiint_{\Omega} f(x,y,z)\mathrm d V=\int_c^d \mathrm d z\iint_{D_z} f(x,y,z)\mathrm d x\mathrm d y
∭ Ω f ( x , y , z ) d V = ∫ c d d z ∬ D z f ( x , y , z ) d x d y
尽可能画出积分区域。
化三重积分 ∭ Ω f ( x , y , z ) d V \displaystyle \iiint_{\Omega} f(x,y,z)\mathrm d V ∭ Ω f ( x , y , z ) d V
其中 Ω \Omega Ω x + 2 y + 3 z = 1 x+2y+3z=1 x + 2 y + 3 z = 1 x = 0 , y = 0 , z = 0 x=0,y=0,z=0 x = 0 , y = 0 , z = 0
∭ Ω f ( x , y , z ) d V = ∬ D x y d x d y ∫ 0 1 3 ( 1 − x − 2 y ) f ( x , y , z ) d z = ∫ 0 1 d x ∫ 0 1 2 ( 1 − x ) d y ∫ 0 1 3 ( 1 − x − 2 y ) f ( x , y , z ) d z \begin{aligned}
\iiint_{\Omega} f(x,y,z) \mathrm dV &= \iint_{D_{xy}} \mathrm d x\mathrm d y\int_0^{\frac{1}{3} (1-x-2y)} f(x,y,z)\mathrm d z\\
&= \int_0^1 \mathrm d x\int_0^{\frac{1}{2}(1-x)} \mathrm d y\int_0^{\frac{1}{3} (1-x-2y)} f(x,y,z)\mathrm d z
\end{aligned}
∭ Ω f ( x , y , z ) d V = ∬ D x y d x d y ∫ 0 3 1 ( 1 − x − 2 y ) f ( x , y , z ) d z = ∫ 0 1 d x ∫ 0 2 1 ( 1 − x ) d y ∫ 0 3 1 ( 1 − x − 2 y ) f ( x , y , z ) d z
当 f ( x , y , z ) = x f(x,y,z)=x f ( x , y , z ) = x
∫ 0 1 x d x ∫ 0 1 2 ( 1 − x ) d y ∫ 0 1 3 ( 1 − x − 2 y ) d z = 1 3 ∫ 0 1 x ⋅ 1 4 ( 1 − x ) 2 d x \int_0^1 x\mathrm d x\int_0^{\frac{1}{2}(1-x)} \mathrm d y\int_0^{\frac{1}{3} (1-x-2y)} \mathrm d z=\frac{1}{3} \int_0^1 x \cdot \frac{1}{4} (1-x)^2 \mathrm d x
∫ 0 1 x d x ∫ 0 2 1 ( 1 − x ) d y ∫ 0 3 1 ( 1 − x − 2 y ) d z = 3 1 ∫ 0 1 x ⋅ 4 1 ( 1 − x ) 2 d x
**当被积函数只含一个变量时,常用方法是利用截面法先对该变量定限,因为可以凑出面积。**注意,如果面积是一个圆,需要带 π \pi π
I = ∭ Ω x d x d y d z = ∫ 0 1 x d x ∬ D x d y d z = ∫ 0 1 x S ( D x ) d x I=\iiint_\Omega x\mathrm d x\mathrm d y\mathrm d z=\int_0^1 x\mathrm d x\iint_{D_x} \mathrm d y\mathrm d z=\int_0^1 x S(D_x) \mathrm d x
I = ∭ Ω x d x d y d z = ∫ 0 1 x d x ∬ D x d y d z = ∫ 0 1 x S ( D x ) d x
计算三重积分
∭ Ω e y d x d y d z \iiint_{\Omega} e^y \mathrm d x\mathrm d y\mathrm d z
∭ Ω e y d x d y d z
其中积分区域 Ω \Omega Ω x 2 − y 2 + z 2 = 1 x^2-y^2+z^2=1 x 2 − y 2 + z 2 = 1 y = 0 , y = 2 y=0,y=2 y = 0 , y = 2
是 x 2 − y 2 = 1 x^2-y^2=1 x 2 − y 2 = 1 x o z xoz x o z
∭ Ω e y d x d y d z = ∫ 0 2 e y d y ∬ D y d x d z = 3 π ( e 2 − 1 ) \iiint_{\Omega} e^y \mathrm d x\mathrm d y\mathrm d z=\int_0^2 e^y \mathrm d y\iint_{D_y}\mathrm d x\mathrm d z=3\pi (e^2-1)
∭ Ω e y d x d y d z = ∫ 0 2 e y d y ∬ D y d x d z = 3 π ( e 2 − 1 )
化三重积分
∭ Ω f ( x , y , z ) d V \iiint_{\Omega} f(x,y,z)\mathrm d V
∭ Ω f ( x , y , z ) d V
为累次积分,其中积分区域 $\Omega $ 由曲面 x 2 + y 2 − z 2 4 = 1 \displaystyle x^2+y^2-\frac{z^2}{4}=1 x 2 + y 2 − 4 z 2 = 1 z = 0 , z = 2 z=0,z=2 z = 0 , z = 2
利用柱线法,先画出积分区域图
需要分两部分 D 1 = { ( x , y ) ∣ x 2 + y 2 ≤ 1 } D_1=\{(x,y)\mid x^2+y^2 \le 1\} D 1 = { ( x , y ) ∣ x 2 + y 2 ≤ 1 } D 2 = { ( x , y ) ∣ 1 ≤ x 2 + y 2 ≤ 4 } D_2=\{(x,y)\mid 1 \le x^2+y^2 \le 4\} D 2 = { ( x , y ) ∣ 1 ≤ x 2 + y 2 ≤ 4 }
利用截面法
定理:设变换 T : { x = x ( u , v , w ) y = y ( u , v , w ) z = z ( u , v , w ) T:\left\{\begin{array}{l}x=x(u, v, w) \\ y=y(u, v, w) \\ z=z(u, v, w)\end{array}\right. T : ⎩ ⎨ ⎧ x = x ( u , v , w ) y = y ( u , v , w ) z = z ( u , v , w ) u v w u v w u v w Ω 1 \Omega_1 Ω 1 x y z x y z x y z Ω \Omega Ω
x ( u , v , w ) , y ( u , v , w ) , z ( u , v , w ) ∈ C 1 ( Ω 1 ) x(u, v, w), y(u, v, w), z(u, v, w) \in C^1\left(\Omega_1\right) x ( u , v , w ) , y ( u , v , w ) , z ( u , v , w ) ∈ C 1 ( Ω 1 )
J = ∂ ( x , y , z ) ∂ ( u , v , w ) ≠ 0 , ( u , v , w ) ∈ Ω 1 \displaystyle J=\frac{\partial(x, y, z)}{\partial(u, v, w)} \neq 0,(u, v, w) \in \Omega_1 J = ∂ ( u , v , w ) ∂ ( x , y , z ) = 0 , ( u , v , w ) ∈ Ω 1
f ( x , y , z ) ∈ C ( Ω ) f(x, y, z) \in C(\Omega) f ( x , y , z ) ∈ C ( Ω )
则
∭ Ω f ( x , y , z ) d V = ∭ Ω 1 f [ x ( u , v , w ) , y ( u , v , w ) , z ( u , v , w ) ] ⋅ ∣ J ∣ ⋅ d u d v d w \iiint_\Omega f(x,y,z)\mathrm d V=
\iiint_{\Omega_1} f[x(u,v,w),y(u,v,w),z(u,v,w)] \cdot |J|\cdot \mathrm d u\mathrm d v\mathrm d w
∭ Ω f ( x , y , z ) d V = ∭ Ω 1 f [ x ( u , v , w ) , y ( u , v , w ) , z ( u , v , w ) ] ⋅ ∣ J ∣ ⋅ d u d v d w
其中 J = ∂ ( x , y , z ) ∂ ( u , v , w ) = ∣ x u x v x w y u y v y w z u z v z w ∣ \displaystyle J=\frac{\partial (x,y,z)}{\partial(u,v,w)}=\begin{vmatrix}x_u & x_v & x_w\\y_u & y_v & y_w\\z_u & z_v & z_w\end{vmatrix} J = ∂ ( u , v , w ) ∂ ( x , y , z ) = ∣ ∣ ∣ ∣ ∣ ∣ x u y u z u x v y v z v x w y w z w ∣ ∣ ∣ ∣ ∣ ∣
∭ Ω f ( x , y , z ) d V = ∭ Ω f ( r cos θ , r sin θ , z ) ⋅ r d r d θ d z \iiint_\Omega f(x,y,z)\mathrm d V =\iiint_\Omega f(r\cos \theta,r\sin\theta,z)\cdot r\mathrm d r\mathrm d \theta\mathrm d z
∭ Ω f ( x , y , z ) d V = ∭ Ω f ( r cos θ , r sin θ , z ) ⋅ r d r d θ d z
计算三重积分
∭ Ω z d x d y d z \iiint_\Omega z\mathrm d x\mathrm d y\mathrm d z
∭ Ω z d x d y d z
其中积分区域 Ω : x 2 + y 2 + z 2 ≤ 2 , z ≥ x 2 + y 2 \Omega:\ x^2+y^2+z^2 \le 2,z\ge x^2+y^2 Ω : x 2 + y 2 + z 2 ≤ 2 , z ≥ x 2 + y 2
被积函数只有一个变量,截面法 ,分为两个区域
D z 1 = { ( x , y ) ∣ x 2 + y 2 ≤ z , ( 0 ≤ z ≤ 1 ) } D z 1 = { ( x , y ) ∣ x 2 + y 2 ≤ 2 − z 2 , ( 1 ≤ z ≤ 2 ) } D_{z_1}=\{(x,y)\mid x^2+y^2\le z ,(0\le z\le 1)\}\\
D_{z_1}=\{(x,y)\mid x^2+y^2 \le 2-z^2 ,(1\le z \le \sqrt{2})\}
D z 1 = { ( x , y ) ∣ x 2 + y 2 ≤ z , ( 0 ≤ z ≤ 1 ) } D z 1 = { ( x , y ) ∣ x 2 + y 2 ≤ 2 − z 2 , ( 1 ≤ z ≤ 2 ) }
如果用柱线法,则会比较复杂。
计算三重积分
∭ Ω z x 2 + y 2 d V \iiint_\Omega \frac{z}{\sqrt{x^2+y^2}}\mathrm d V
∭ Ω x 2 + y 2 z d V
其中积分区域 Ω \Omega Ω y o z yoz y o z
D = { ( y , z ) ∣ y 2 + z 2 ≤ 1 , z ≥ 2 y − 1 , y ≥ 0 , z ≥ 0 } D=\{(y,z)\mid y^2+z^2 \le 1,z\ge 2y-1,y\ge 0,z\ge 0\}
D = { ( y , z ) ∣ y 2 + z 2 ≤ 1 , z ≥ 2 y − 1 , y ≥ 0 , z ≥ 0 }
绕 z z z
旋转曲面方程是什么,绕 z z z y 2 y^2 y 2 x 2 + y 2 x^2+y^2 x 2 + y 2
x 2 + y 2 + z 2 ≤ 1 x^2+y^2+z^2\le 1 x 2 + y 2 + z 2 ≤ 1 y = 1 + z 2 y=\frac{1+z}{2} y = 2 1 + z x 2 + y 2 ≤ ( 1 + z 2 ) 2 x^2+y^2 \le (\frac{1+z}{2})^2 x 2 + y 2 ≤ ( 2 1 + z ) 2
利用截面法
D z 1 = { ( x , y ) ∣ x 2 + y 2 ≤ ( z + 1 2 ) 2 , 0 ≤ z ≤ 3 5 } , D z 2 = { ( x , y ) ∣ x 2 + y 2 ≤ 1 − z 2 , 3 5 ≤ z ≤ 1 } , \begin{aligned}
& D_{z_1}=\left\{(x, y) \mid x^2+y^2 \leq\left(\frac{z+1}{2}\right)^2, 0 \leq z \leq \frac{3}{5}\right\}, \\
& D_{z_2}=\left\{(x, y) \mid x^2+y^2 \leq 1-z^2, \frac{3}{5} \leq z \leq 1\right\},
\end{aligned}
D z 1 = { ( x , y ) ∣ x 2 + y 2 ≤ ( 2 z + 1 ) 2 , 0 ≤ z ≤ 5 3 } , D z 2 = { ( x , y ) ∣ x 2 + y 2 ≤ 1 − z 2 , 5 3 ≤ z ≤ 1 } ,
利用柱面坐标得:
∫ 0 3 5 z d z ∫ 0 2 π d θ ∫ 0 z + 1 2 1 r ⋅ r d r + ∫ 3 5 1 z d z ∫ 0 2 π d θ ∫ 0 1 − z 2 1 r ⋅ r d r = 89 150 π \int_0^{\frac{3}{5}} z \mathrm{~d} z \int_0^{2 \pi} \mathrm{d} \theta \int_0^{\frac{z+1}{2}} \frac{1}{r} \cdot r \mathrm{~d} r+\int_{\frac{3}{5}}^1 z \mathrm{~d} z \int_0^{2 \pi} \mathrm{d} \theta \int_0^{\sqrt{1-z^2}} \frac{1}{r} \cdot r \mathrm{~d} r=\frac{89}{150} \pi
∫ 0 5 3 z d z ∫ 0 2 π d θ ∫ 0 2 z + 1 r 1 ⋅ r d r + ∫ 5 3 1 z d z ∫ 0 2 π d θ ∫ 0 1 − z 2 r 1 ⋅ r d r = 1 5 0 8 9 π
设 M ( x , y , z ) M(x,y,z) M ( x , y , z ) ρ = ∣ O M → ∣ \rho=|\overrightarrow{OM}| ρ = ∣ O M ∣ φ \varphi φ ∣ O M → ∣ |\overrightarrow {OM}| ∣ O M ∣ z z z φ \varphi φ θ \theta θ ∣ O M → ∣ |\overrightarrow{OM}| ∣ O M ∣ x o y xoy x o y ∣ O P → ∣ |\overrightarrow{OP}| ∣ O P ∣ x x x x o y xoy x o y θ \theta θ ( ρ , θ , φ ) (\rho,\theta,\varphi) ( ρ , θ , φ ) M M M
规定:
ρ ≥ 0 , 0 ≤ θ ≤ 2 π , 0 ≤ φ ≤ π \rho\ge0,0\le \theta\le 2\pi,0\le \varphi \le \pi
ρ ≥ 0 , 0 ≤ θ ≤ 2 π , 0 ≤ φ ≤ π
由 直角三角形 相应关系得到
{ r = ρ sin φ x = r cos θ = ρ sin φ cos θ y = ρ sin φ sin θ z = ρ cos φ \left\{
\begin{aligned}
&r=\rho\sin\varphi\\
&x=r\cos\theta=\rho\sin\varphi\cos \theta\\
&y=\rho\sin\varphi\sin\theta\\
&z=\rho\cos \varphi
\end{aligned}
\right.
⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ r = ρ sin φ x = r cos θ = ρ sin φ cos θ y = ρ sin φ sin θ z = ρ cos φ

对三个元素的增量,划定一个区域。
∭ Ω f ( x , y , z ) d V = ∭ Ω f ( ρ sin φ cos θ , ρ sin φ sin θ , ρ cos φ ) ⋅ ρ 2 sin φ d ρ d θ d φ \iiint_\Omega f(x,y,z)\mathrm d V=\iiint_\Omega f(\rho\sin\varphi\cos \theta,\rho\sin\varphi\sin\theta,\rho\cos\varphi)\cdot \rho^2 \sin\varphi\mathrm d \rho\mathrm d \theta\mathrm d \varphi
∭ Ω f ( x , y , z ) d V = ∭ Ω f ( ρ sin φ cos θ , ρ sin φ sin θ , ρ cos φ ) ⋅ ρ 2 sin φ d ρ d θ d φ
计算三重积分
∭ Ω x 2 + y 2 + z 2 d x d y d z \iiint_\Omega \sqrt{x^2+y^2+z^2}\mathrm d x\mathrm d y\mathrm d z
∭ Ω x 2 + y 2 + z 2 d x d y d z
其中积分区域 Ω : x 2 + y 2 ≤ z 2 , x 2 + y 2 + z 2 ≤ R 2 , z ≥ 0 \Omega:x^2+y^2 \le z^2,x^2+y^2+z^2 \le R^2,z\ge 0 Ω : x 2 + y 2 ≤ z 2 , x 2 + y 2 + z 2 ≤ R 2 , z ≥ 0
先求出交线 z = 2 2 R z=\frac{\sqrt{2}}{2}R z = 2 2 R
原式:
∭ Ω ρ ⋅ ρ 2 sin φ d ρ d θ d φ \iiint_\Omega \rho\cdot\rho^2 \sin\varphi \mathrm d \rho\mathrm d \theta\mathrm d \varphi
∭ Ω ρ ⋅ ρ 2 sin φ d ρ d θ d φ
三个独立的定积分。θ \theta θ φ \varphi φ 0 0 0 π / 4 \pi/4 π / 4
∫ 0 2 π d θ ∫ 0 π 4 sin φ d φ ∫ 0 R ρ 3 d ρ \int_0^{2\pi}\mathrm d \theta\int_0^\frac{\pi}{4} \sin\varphi\mathrm d \varphi\int_0^R \rho^3 \mathrm d\rho
∫ 0 2 π d θ ∫ 0 4 π sin φ d φ ∫ 0 R ρ 3 d ρ
设函数 f ( x ) f(x) f ( x ) [ 0 , 1 ] [0,1] [ 0 , 1 ] f ( 0 ) = 0 f(0)=0 f ( 0 ) = 0 f ′ ( 0 ) f'(0) f ′ ( 0 )
lim t → 0 1 t 4 ∭ x 2 + y 2 + z 2 ≤ t 2 f ( x 2 + y 2 + z 2 ) d V \lim_{t\to 0}\frac{1}{t^4} \iiint_{x^2+y^2+z^2 \le t^2} f(\sqrt{x^2+y^2+z^2}) \mathrm d V
t → 0 lim t 4 1 ∭ x 2 + y 2 + z 2 ≤ t 2 f ( x 2 + y 2 + z 2 ) d V
洛必达法则……
如果是球体:
∭ x 2 + y 2 + z 2 f ( ρ ) d V = ∫ 0 2 π d θ ∫ 0 π sin φ d φ ∫ 0 t f ( ρ ) ⋅ ρ 2 d ρ = 4 π ∫ 0 t f ( ρ ) ⋅ ρ 2 d ρ \iiint_{x^2+y^2+z^2} f(\rho)\mathrm d V=\int_0^{2\pi} \mathrm d \theta \int_0^\pi \sin\varphi \mathrm d \varphi \int_0^t f(\rho) \cdot \rho^2 \mathrm d \rho=4\pi\int_0^t f(\rho) \cdot \rho^2 \mathrm d \rho
∭ x 2 + y 2 + z 2 f ( ρ ) d V = ∫ 0 2 π d θ ∫ 0 π sin φ d φ ∫ 0 t f ( ρ ) ⋅ ρ 2 d ρ = 4 π ∫ 0 t f ( ρ ) ⋅ ρ 2 d ρ
lim t → 0 1 t 4 ∭ x 2 + y 2 + z 2 ≤ t 2 f ( x 2 + y 2 + z 2 ) d V = lim t → 0 4 π ∫ 0 t f ( ρ ) ⋅ ρ 2 d ρ t 4 = lim t → 0 4 π f ( t ) ⋅ t 2 4 t 3 = π f ′ ( 0 ) \lim_{t\to 0}\frac{1}{t^4} \iiint_{x^2+y^2+z^2 \le t^2} f(\sqrt{x^2+y^2+z^2}) \mathrm d V=\lim_{t \to 0}\frac{4\pi \int_0^t f(\rho)\cdot \rho^2\mathrm d \rho}{t^4}=\lim_{t\to0}\frac{4\pi f(t)\cdot t^2}{4t^3}=\pi f'(0)
t → 0 lim t 4 1 ∭ x 2 + y 2 + z 2 ≤ t 2 f ( x 2 + y 2 + z 2 ) d V = t → 0 lim t 4 4 π ∫ 0 t f ( ρ ) ⋅ ρ 2 d ρ = t → 0 lim 4 t 3 4 π f ( t ) ⋅ t 2 = π f ′ ( 0 )
注意最后一步不能洛必达。
轮换性的使用条件:积分区域轮换对称 。
计算三重积分
∭ Ω ( 2 x 2 + 3 y 2 − 4 z 2 ) d x d y d z \iiint_\Omega (2x^2+3y^2-4z^2) \mathrm d x\mathrm d y\mathrm d z
∭ Ω ( 2 x 2 + 3 y 2 − 4 z 2 ) d x d y d z
其中积分区域 Ω : x 2 + y 2 + z 2 ≤ 1 \Omega:x^2+y^2+z^2 \le 1 Ω : x 2 + y 2 + z 2 ≤ 1
球坐标不好计算。
由轮换性可以得到
∭ Ω x 2 d V = ∭ Ω y 2 d V = ∭ Ω z 2 d V \iiint_\Omega x^2\mathrm d V=\iiint_\Omega y^2\mathrm d V=\iiint_\Omega z^2\mathrm d V
∭ Ω x 2 d V = ∭ Ω y 2 d V = ∭ Ω z 2 d V
所以,原式(转化为 对称 形式)
\frac{1}{3} \iiint_{\Omega} (x^2+y^2+z^2) \mathrm d V=\frac{1}{3}\int_0^{2\pi}\mathrm d \theta\int_0^\pi \mathrm \sin\varphi d \varphi \int_0^1 \rho^2 \cdot \rho^2 \mathrm d \rho
计算三重积分
∭ Ω ( x 2 + y 2 − z 2 ) d x d y d z \iiint_\Omega (x^2+y^2-z^2)\mathrm d x\mathrm d y\mathrm d z
∭ Ω ( x 2 + y 2 − z 2 ) d x d y d z
其中积分区域
Ω : x 2 a 2 + y 2 b 2 + z 2 c 2 ≤ 1 \Omega:\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2} \le 1
Ω : a 2 x 2 + b 2 y 2 + c 2 z 2 ≤ 1
x = a X , y = b Y , z = c Z x=aX,y=bY,z=cZ
x = a X , y = b Y , z = c Z
由轮换性可以得到
∭ Ω X 2 d V = ∭ Ω Y 2 d V = ∭ Ω Z 2 d V \iiint_\Omega X^2\mathrm d V=\iiint_\Omega Y^2\mathrm d V=\iiint_\Omega Z^2\mathrm d V
∭ Ω X 2 d V = ∭ Ω Y 2 d V = ∭ Ω Z 2 d V
也就是
∭ Ω x 2 / a 2 d V = ∭ Ω y 2 / b 2 d V = ∭ Ω z 2 / c 2 d V \iiint_\Omega x^2/a^2\mathrm d V=\iiint_\Omega y^2/b^2\mathrm d V=\iiint_\Omega z^2/c^2\mathrm d V
∭ Ω x 2 / a 2 d V = ∭ Ω y 2 / b 2 d V = ∭ Ω z 2 / c 2 d V
利用截面法:
∭ Ω x 2 a 2 d V = 1 a 2 ∫ − a a x 2 d x ∬ D x d y d z = 1 a 2 ∫ − a a x 2 ⋅ π b c ( 1 − x 2 a 2 ) ⏟ 椭 圆 面 积 d x = I \iiint_\Omega \frac{x^2}{a^2}\mathrm d V=\frac{1}{a^2} \int_{-a}^a x^2\mathrm d x\iint_{D_x}\mathrm d y\mathrm d z=\frac{1}{a^2} \int_{-a}^a x^2 \cdot \underbrace{\pi bc\left(1-\frac{x^2}{a^2}\right)}_{椭圆面积}\mathrm d x=I
∭ Ω a 2 x 2 d V = a 2 1 ∫ − a a x 2 d x ∬ D x d y d z = a 2 1 ∫ − a a x 2 ⋅ 椭 圆 面 积 π b c ( 1 − a 2 x 2 ) d x = I
∭ Ω ( x 2 + y 2 − z 2 ) d x d y d z = ( a 2 + b 2 − c 2 ) × I \iiint_\Omega (x^2+y^2-z^2)\mathrm d x\mathrm d y\mathrm d z=(a^2+b^2-c^2)\times I
∭ Ω ( x 2 + y 2 − z 2 ) d x d y d z = ( a 2 + b 2 − c 2 ) × I
也可以利用广义球面坐标计算。
如果积分区域 Ω \Omega Ω y o z yoz y o z ,且 f ( x , y , z ) f(x,y,z) f ( x , y , z ) 是 x x x ,即 f ( − x , y , z ) = − f ( x , y , z ) f(-x,y,z)=-f(x,y,z) f ( − x , y , z ) = − f ( x , y , z )
则 ∭ Ω f ( x , y , z ) d V = 0 \iiint_\Omega f(x,y,z)\mathrm d V=0 ∭ Ω f ( x , y , z ) d V = 0
计算三重积分
∭ Ω ( x + y + z ) 2 d x d y d z \iiint_{\Omega} (x+y+z)^2 \mathrm d x\mathrm d y\mathrm d z
∭ Ω ( x + y + z ) 2 d x d y d z
其中积分区域 Ω : x 2 + y 2 + z 2 ≤ 2 , z ≥ x 2 + y 2 \Omega:x^2+y^2+z^2 \le 2,z \ge x^2+y^2 Ω : x 2 + y 2 + z 2 ≤ 2 , z ≥ x 2 + y 2 φ \varphi φ z z z
对称性:由关于 y o z yoz y o z x y + x z xy+xz x y + x z x o z xoz x o z y z yz y z
剩下
∭ Ω z 2 d V ⏟ 截 面 法 , 只 有 z 一 个 变 量 + ∭ Ω ( x 2 + y 2 ) d V ⏟ 柱 面 坐 标 \underbrace{\iiint_{\Omega} z^2 \mathrm d V}_{截面法,只有z一个变量}+\underbrace{\iiint_\Omega (x^2+y^2)\mathrm d V}_{柱面坐标}
截 面 法 , 只 有 z 一 个 变 量 ∭ Ω z 2 d V + 柱 面 坐 标 ∭ Ω ( x 2 + y 2 ) d V
∭ Ω ( x 2 + y 2 ) d V = ∫ 0 2 π d θ ∫ 0 1 r d r ∫ r 2 2 − r 2 r 2 d z \iiint_\Omega (x^2+y^2)\mathrm d V=\int_0^{2\pi}\mathrm d \theta\int_0^1 r\mathrm d r\int_{r^2}^{\sqrt{2-r^2}} r^2 \mathrm d z
∭ Ω ( x 2 + y 2 ) d V = ∫ 0 2 π d θ ∫ 0 1 r d r ∫ r 2 2 − r 2 r 2 d z
先 x o y xoy x o y z z z

球面坐标+对称性。
立体的体积可以利用二重积分计算(函数是柱线法里面的),也可以利用三重积分(被积函数取 1 即可)。
计算 x 2 + y 2 + z 2 ≤ 2 z x^2+y^2+z^2\le2z x 2 + y 2 + z 2 ≤ 2 z x 2 + y 2 ≤ 3 2 z x^2+y^2 \le \frac{3}{2}z x 2 + y 2 ≤ 2 3 z
$$
V=\underbrace{8}_{八个部分}\int_0^r (r^2-x^2)\mathrm d x
$$
V = 8 ∫ 0 1 ( 1 − z 2 ) z d z = 2 V=8\int_0^1 (1-z^2)z\mathrm d z=2
V = 8 ∫ 0 1 ( 1 − z 2 ) z d z = 2

三圆柱体是由三个垂直圆柱相交形成的实体:
x 2 + y 2 = r 2 x 2 + z 2 = r 2 y 2 + z 2 = r 2 x^2+y^2 =r^2\\
x^2+z^2=r^2\\
y^2+z^2=r^2
x 2 + y 2 = r 2 x 2 + z 2 = r 2 y 2 + z 2 = r 2
三圆柱体的体积公式
第一种方法是使用牟合方盖,然后再把积分投影的平面区域设为一个圆,原式化为:
16 ∫ 0 π 4 d θ ∫ 0 1 1 − r 2 cos 2 θ r d r 16\int_0^\frac{\pi}{4} \mathrm d \theta\int_0^1 \sqrt{1-r^2\cos^2\theta}r\mathrm d r
1 6 ∫ 0 4 π d θ ∫ 0 1 1 − r 2 cos 2 θ r d r
第二种是分割为一个正方体和六个盖子。
V c u b e = ( 2 r ) 3 V c a p = ∫ r / 2 r 4 ( r 2 − x 2 ) d x = 1 3 ( 8 − 5 2 ) r 3 V_{\mathrm{cube}}=(\sqrt{2}r)^3\quad V_{\mathrm{cap}}=\int_{r/\sqrt{2}}^r 4(r^2-x^2)\mathrm d x=\frac{1}{3}(8-5\sqrt{2})r^3
V c u b e = ( 2 r ) 3 V c a p = ∫ r / 2 r 4 ( r 2 − x 2 ) d x = 3 1 ( 8 − 5 2 ) r 3
设曲面 Σ \Sigma Σ z = f ( x , y ) z=f(x,y) z = f ( x , y ) Σ \Sigma Σ z z z Σ \Sigma Σ Δ S \Delta S Δ S x o y xoy x o y d σ \mathrm d \sigma d σ M ( x , y , z ) M(x,y,z) M ( x , y , z ) Δ S \Delta S Δ S M M M Δ S \Delta S Δ S d S \mathrm d S d S d s \mathrm d s d s
投影角度 γ \gamma γ
cos γ = cos ( n , k ) ^ = 1 f x 2 + f y 2 + 1 d σ d S = ∣ cos y ∣ \cos \gamma=\cos \widehat{(\boldsymbol n,\boldsymbol k)}=\frac{1}{\sqrt{f_x^2+f_y^2+1}}\quad \frac{\mathrm d \sigma}{\mathrm d S}=|\cos y\, |
cos γ = cos ( n , k ) = f x 2 + f y 2 + 1 1 d S d σ = ∣ cos y ∣
曲面 Σ \Sigma Σ
S = ∬ D x y d S = ∬ D x y 1 + f x 2 + f y 2 d x d y = ∬ D ( d x d y ) 2 + ( d y d z ) 2 + ( d z d x ) 2 S=\iint_{D_{xy}}\mathrm d S=\boxed{\iint_{D_{xy}} \sqrt{1+f_x^2+f_y^2}\mathrm d x\mathrm d y}\\
=\iint_D\sqrt{(\mathrm d x\mathrm d y)^2+(\mathrm d y\mathrm d z)^2+(\mathrm d z\mathrm d x)^2}
S = ∬ D x y d S = ∬ D x y 1 + f x 2 + f y 2 d x d y = ∬ D ( d x d y ) 2 + ( d y d z ) 2 + ( d z d x ) 2
双参数方程 设曲面 Σ \Sigma Σ { x = x ( u , v ) y = y ( u , v ) , z = z ( u , v ) \left\{\begin{array}{l}x=x(u, v) \\ y=y(u, v) \text {, } \\ z=z(u, v)\end{array}\right. ⎩ ⎨ ⎧ x = x ( u , v ) y = y ( u , v ) , z = z ( u , v ) ∂ ( y , z ) ∂ ( u , v ) , ∂ ( z , x ) ∂ ( u , v ) , ∂ ( x , y ) ∂ ( u , v ) \displaystyle \frac{\partial(y, z)}{\partial(u, v)}, \frac{\partial(z, x)}{\partial(u, v)}, \frac{\partial(x, y)}{\partial(u, v)} ∂ ( u , v ) ∂ ( y , z ) , ∂ ( u , v ) ∂ ( z , x ) , ∂ ( u , v ) ∂ ( x , y ) Σ \Sigma Σ
A = ∂ ( y , z ) ∂ ( u , v ) , B = ∂ ( z , x ) ∂ ( u , v ) , C = ∂ ( x , y ) ∂ ( u , v ) A=\frac{\partial(y, z)}{\partial(u, v)}, B=\frac{\partial(z, x)}{\partial(u, v)}, C=\frac{\partial(x, y)}{\partial(u, v)}
A = ∂ ( u , v ) ∂ ( y , z ) , B = ∂ ( u , v ) ∂ ( z , x ) , C = ∂ ( u , v ) ∂ ( x , y )
则曲面 Σ \Sigma Σ n ⃗ = { A , B , C } \vec{n}=\{A, B, C\} n = { A , B , C }
当 C ≠ 0 C \neq 0 C = 0 d σ = d x d y = ∣ C ∣ d u d v \mathrm{d} \sigma=\mathrm{d} x \mathrm{d} y=|C| \mathrm{d} u \mathrm{d} v d σ = d x d y = ∣ C ∣ d u d v ∣ cos γ ∣ = ∣ C ∣ A 2 + B 2 + C 2 \displaystyle |\cos \gamma\, |=\frac{|C|}{\sqrt{A^2+B^2+C^2}} ∣ cos γ ∣ = A 2 + B 2 + C 2 ∣ C ∣
d S = 1 ∣ cos γ ∣ d x d y = A 2 + B 2 + C 2 d u d v \mathrm{d} S=\frac{1}{|\cos \gamma\,|} \mathrm{d} x \mathrm{d} y=\sqrt{A^2+B^2+C^2} \mathrm{~d} u \mathrm{d} v
d S = ∣ cos γ ∣ 1 d x d y = A 2 + B 2 + C 2 d u d v
其中 d S \mathrm d S d S
因此,曲面面积为:
S = ∬ D u v A 2 + B 2 + C 2 d u d v S=\iint_{D_{u v}} \sqrt{A^2+B^2+C^2} \mathrm{~d} u \mathrm{d} v
S = ∬ D u v A 2 + B 2 + C 2 d u d v
球面的双参数方程:
x = R sin φ cos θ y = R sin φ sin θ z = R cos φ x=R\sin\varphi\cos \theta \quad y=R\sin\varphi\sin\theta\quad z=R\cos\varphi
x = R sin φ cos θ y = R sin φ sin θ z = R cos φ
其中 0 ≤ φ ≤ π , 0 ≤ θ ≤ 2 π 0\le \varphi \le \pi,0 \le \theta \le 2\pi 0 ≤ φ ≤ π , 0 ≤ θ ≤ 2 π
∂ ( y , z ) ∂ ( φ , θ ) = R 2 sin 2 φ cos θ , ∂ ( z , x ) ∂ ( φ , θ ) = R 2 sin 2 φ sin θ , ∂ ( x , y ) ∂ ( φ , θ ) = R 2 sin φ cos θ , A 2 + B 2 + C 2 = R 2 sin φ , \begin{gathered}
\frac{\partial(y, z)}{\partial(\varphi, \theta)}=R^2 \sin ^2 \varphi \cos \theta, \frac{\partial(z, x)}{\partial(\varphi, \theta)}=R^2 \sin ^2 \varphi \sin \theta, \frac{\partial(x, y)}{\partial(\varphi, \theta)}=R^2 \sin \varphi \cos \theta, \\
\sqrt{A^2+B^2+C^2}=R^2 \sin \varphi,
\end{gathered}
∂ ( φ , θ ) ∂ ( y , z ) = R 2 sin 2 φ cos θ , ∂ ( φ , θ ) ∂ ( z , x ) = R 2 sin 2 φ sin θ , ∂ ( φ , θ ) ∂ ( x , y ) = R 2 sin φ cos θ , A 2 + B 2 + C 2 = R 2 sin φ ,
故球面的面积为:
S = ∬ D R 2 sin φ d φ d θ = R 2 ∫ 0 2 π d θ ∫ 0 π sin φ d φ = 4 π R 2 S=\iint_D R^2 \sin \varphi \mathrm{d} \varphi \mathrm{d} \theta=R^2 \int_0^{2 \pi} \mathrm{d} \theta \int_0^\pi \sin \varphi \mathrm{d} \varphi=4 \pi R^2
S = ∬ D R 2 sin φ d φ d θ = R 2 ∫ 0 2 π d θ ∫ 0 π sin φ d φ = 4 π R 2
求锥面 z 2 = x 2 + y 2 z^2=x^2+y^2 z 2 = x 2 + y 2 z 2 = 2 y z^2=2y z 2 = 2 y
锥面 S S S z = x 2 + y 2 z=\sqrt{x^2+y^2} z = x 2 + y 2
∂ z ∂ x = x x 2 + y 2 , ∂ z ∂ y = y x 2 + y 2 , d S = 2 d x d y \frac{\partial z}{\partial x}=\frac{x}{\sqrt{x^2+y^2}},\frac{\partial z}{\partial y}=\frac{y}{\sqrt{x^2+y^2}},\mathrm d S=\sqrt{2}\mathrm d x\mathrm d y
∂ x ∂ z = x 2 + y 2 x , ∂ y ∂ z = x 2 + y 2 y , d S = 2 d x d y
注意投影区域是一个圆。
设 x o y xoy x o y y = f ( x ) , a ≤ x ≤ b y=f(x),a\le x\le b y = f ( x ) , a ≤ x ≤ b f ( x ) ≥ 0 f(x)\ge 0 f ( x ) ≥ 0 x x x
绕 x x x z = f 2 ( x ) − y 2 z=\sqrt{f^2(x)-y^2} z = f 2 ( x ) − y 2
曲面面积元素为:
d S = f ( x ) [ f ′ ( x ) ] 2 + 1 f 2 ( x ) − y 2 d x d y \mathrm d S=\frac{f(x)\sqrt{[f'(x)]^2+1}}{\sqrt{f^2(x)-y^2}}\mathrm d x\mathrm d y
d S = f 2 ( x ) − y 2 f ( x ) [ f ′ ( x ) ] 2 + 1 d x d y
S = 2 ∬ D d S = 2 ∬ D f ( x ) [ f ′ ( x ) ] 2 + 1 f 2 ( x ) − y 2 d x d y = 2 ∫ a b d x ∫ − f ( x ) f ( x ) f ( x ) [ f ′ ( x ) ] 2 + 1 f 2 ( x ) − y 2 d y = 2 π ∫ a b f ( x ) [ f ′ ( x ) ] 2 + 1 d x \begin{aligned}
S & =2 \iint_D \mathrm{~d} S=2 \iint_D \frac{f(x) \sqrt{\left[f^{\prime}(x)\right]^2+1}}{\sqrt{f^2(x)-y^2}} \mathrm{~d} x d y \\
& =2 \int_a^b \mathrm{~d} x \int_{-f(x)}^{f(x)} \frac{f(x) \sqrt{\left[f^{\prime}(x)\right]^2+1}}{\sqrt{f^2(x)-y^2}} \mathrm{~d} y \\
& =2 \pi \int_a^b f(x) \sqrt{\left[f^{\prime}(x)\right]^2+1} \mathrm{~d} x
\end{aligned}
S = 2 ∬ D d S = 2 ∬ D f 2 ( x ) − y 2 f ( x ) [ f ′ ( x ) ] 2 + 1 d x d y = 2 ∫ a b d x ∫ − f ( x ) f ( x ) f 2 ( x ) − y 2 f ( x ) [ f ′ ( x ) ] 2 + 1 d y = 2 π ∫ a b f ( x ) [ f ′ ( x ) ] 2 + 1 d x
求球面 x 2 + y 2 + z 2 = a 2 x^2+y^2+z^2=a^2 x 2 + y 2 + z 2 = a 2 x 2 + y 2 = a x x^2+y^2=ax x 2 + y 2 = a x
柱面部分的面积。x = r cos θ + a / 2 , y = r sin θ x=r\cos\theta+a/2,y=r\sin\theta x = r cos θ + a / 2 , y = r sin θ r = a / 2 r=a/2 r = a / 2
∫ − π 2 π 2 2 ( a 2 − x 2 − y 2 ) r d θ \int_{-\frac{\pi}{2}}^\frac{\pi}{2} 2(\sqrt{a^2-x^2-y^2})r\mathrm d \theta
∫ − 2 π 2 π 2 ( a 2 − x 2 − y 2 ) r d θ

如果质量 ρ \rho ρ


设一个物体占有空间闭区域 Ω \Omega Ω M ( x , y , z ) M(x, y, z) M ( x , y , z ) ρ ( x , y , z ) \rho(x, y, z) ρ ( x , y , z ) Ω \Omega Ω M 0 ( x 0 , y 0 , z 0 ) M_0\left(x_0, y_0, z_0\right) M 0 ( x 0 , y 0 , z 0 ) m 0 m_0 m 0 M 0 M_0 M 0 M M M d v d v d v d m = ρ ( x , y , z ) d v \mathrm{d} m=\rho(x, y, z) \mathrm{d} v d m = ρ ( x , y , z ) d v M 0 M_0 M 0 M M M r ⃗ \vec{r} r d v \mathrm{d} v d v M 0 M_0 M 0
d F ⃗ = k ⋅ m 0 d m r 2 ⋅ r 0 → = k m 0 ⋅ ρ ( x , y , z ) d v r 3 ⋅ r ⃗ \mathrm{d} \vec{F}=k \cdot \frac{m_0 \mathrm{~d} m}{r^2} \cdot \overrightarrow{r^0}=k m_0 \cdot \frac{\rho(x, y, z) \mathrm{d} v}{r^3} \cdot \vec{r}
d F = k ⋅ r 2 m 0 d m ⋅ r 0 = k m 0 ⋅ r 3 ρ ( x , y , z ) d v ⋅ r
记物体对质点 M 0 M_0 M 0
F ⃗ = { F x , F y , F z } \vec{F}=\left\{F_x, F_y, F_z\right\}
F = { F x , F y , F z }
则:
F x = ∭ Ω k m 0 ⋅ ρ ( x , y , z ) ( x − x 0 ) r 3 ⋅ d V F y = ∭ Ω k m 0 ⋅ ρ ( x , y , z ) ( y − y 0 ) r 3 ⋅ d V F z = ∭ Ω k m 0 ⋅ ρ ( x , y , z ) ( z − z 0 ) r 3 ⋅ d V \begin{aligned}
&F_x=\iiint_{\Omega} k m_0 \cdot \frac{\rho(x, y, z)\left(x-x_0\right)}{r^3} \cdot \mathrm{d}V\\
& F_y=\iiint_{\Omega} k m_0 \cdot \frac{\rho(x, y, z)\left(y-y_0\right)}{r^3} \cdot \mathrm{d}V \\
& F_z=\iiint_{\Omega} k m_0 \cdot \frac{\rho(x, y, z)\left(z-z_0\right)}{r^3} \cdot \mathrm{d}V
\end{aligned}
F x = ∭ Ω k m 0 ⋅ r 3 ρ ( x , y , z ) ( x − x 0 ) ⋅ d V F y = ∭ Ω k m 0 ⋅ r 3 ρ ( x , y , z ) ( y − y 0 ) ⋅ d V F z = ∭ Ω k m 0 ⋅ r 3 ρ ( x , y , z ) ( z − z 0 ) ⋅ d V
选 C C C
使用极坐标代换。
∫ 0 2 π d θ ∫ 0 r ( 1 − cos r 2 ) ⋅ r d r = 2 π ∫ 0 r ( 1 − cos r 2 ) ⏟ r 4 ⋅ r d r = k r 6 \int_0^{2 \pi} {\color{green}\mathrm d \theta} \int_{0}^{r} (1-\cos r^2) \cdot {\color{blue}{r \mathrm d r}}=2\pi \int_{0}^{r} \underbrace{(1-\cos r^2)}_{r^4} \cdot {\color{blue}{r \mathrm d r}} = k r^6
∫ 0 2 π d θ ∫ 0 r ( 1 − cos r 2 ) ⋅ r d r = 2 π ∫ 0 r r 4 ( 1 − cos r 2 ) ⋅ r d r = k r 6
∫ 0 π d θ ∫ sin θ 2 sin θ r 2 ⋅ r d r = 15 2 ∫ 0 π sin 4 θ d θ = 45 π 16 \int_0^{\pi} {\color{green}\mathrm d \theta} \int_{\sin\theta}^{2\sin\theta} r^2 \cdot {\color{blue}{r \mathrm d r}}=\frac{15}{2} \int_0^\pi \sin^4 \theta \mathrm d \theta=\frac{45\pi}{16}
∫ 0 π d θ ∫ sin θ 2 sin θ r 2 ⋅ r d r = 2 1 5 ∫ 0 π sin 4 θ d θ = 1 6 4 5 π
点火公式 。
缩小倍数。


重点积分中值定理的运用比较巧妙。

第一部分直接积分,第二部分极坐标。
\int_0^2 \mathrm d x\int_0^\sqrt{2x-x^2} \frac{x}{\sqrt{2x-x^2}} \mathrm d y+\int_0^\frac{\pi}{2} \mathrm d \theta \int_0^{2\cos \theta } \frac{r\cos \theta}{r} \cdot r \mathrm d r
注意积分上下限。

∫ 0 π d x ∫ 0 π d y ∫ 0 π ∣ cos ( x + y + z ) ∣ d z \int_0^\pi \mathrm d x\int_0^\pi \mathrm d y\int_0^\pi |\cos (x+y+z)\, | \mathrm d z
∫ 0 π d x ∫ 0 π d y ∫ 0 π ∣ cos ( x + y + z ) ∣ d z
考虑积分变量替换:u = x , v = x + y , w = x + y + z u=x,v=x+y,w=x+y+z u = x , v = x + y , w = x + y + z z = w − v , y = v − u z=w-v,y=v-u z = w − v , y = v − u
∫ 0 π d u ∫ u u + π d v ∫ v v + π ∣ cos ( w ) ∣ d w = ∫ 0 π d u ∫ u u + π d v ∫ 0 π ∣ cos ( w ) ∣ d w ⏟ 2 = 2 π 2 \int_0^\pi \mathrm d u \int_u^{u+\pi} \mathrm d v \int_v^{v+\pi} |\cos (w)\, | \mathrm d w=\int_0^\pi \mathrm d u\int_u^{u+\pi}\mathrm d v\underbrace{\int_0^\pi |\cos (w)\,| \mathrm d w}_{2}=2\pi^2
∫ 0 π d u ∫ u u + π d v ∫ v v + π ∣ cos ( w ) ∣ d w = ∫ 0 π d u ∫ u u + π d v 2 ∫ 0 π ∣ cos ( w ) ∣ d w = 2 π 2

变量代换,广义球坐标,注意是半椭球体,因此:
{ x = a sin φ cos θ y = b sin φ sin θ z = c cos φ \left\{
\begin{matrix}
x=a\sin\varphi\cos \theta\\
y=b\sin\varphi\sin\theta\\
z=c\cos \varphi
\end{matrix}
\right.
⎩ ⎨ ⎧ x = a sin φ cos θ y = b sin φ sin θ z = c cos φ
I = ∫ 0 2 π d θ ∫ 0 π 2 d φ ∫ 0 1 sin 3 φ r 4 a b c ⋅ d r = a b c 1 5 ⋅ 2 3 2 π = 4 π 15 a b c I=\int_0^{2\pi} \mathrm d \theta \int_0^ \frac{\pi}{2} \mathrm d \varphi \int_0^1 \sin^3\varphi r^4 abc \cdot \mathrm d r=abc \frac{1}{5} \cdot \frac{2}{3} 2\pi=\frac{4\pi}{15} abc
I = ∫ 0 2 π d θ ∫ 0 2 π d φ ∫ 0 1 sin 3 φ r 4 a b c ⋅ d r = a b c 5 1 ⋅ 3 2 2 π = 1 5 4 π a b c
也可以利用轮换对称性:
I = 2 3 ∫ 0 2 π d θ ∫ 0 π 2 d φ ∫ 0 1 r 2 ⋅ r 2 sin φ a b c d r = 4 π 15 a b c I=\frac{2}{3} \int_0^{2\pi} \mathrm d \theta \int_0^\frac{\pi}{2} \mathrm d \varphi \int_0^1 r^2 \cdot r^2 \sin\varphi abc \mathrm d r=\frac{4\pi}{15} abc
I = 3 2 ∫ 0 2 π d θ ∫ 0 2 π d φ ∫ 0 1 r 2 ⋅ r 2 sin φ a b c d r = 1 5 4 π a b c
求球面 z = a 2 − x 2 − y 2 z=\sqrt{a^2-x^2-y^2} z = a 2 − x 2 − y 2 x 2 + y 2 = a x ( a > 0 ) x^2+y^2=ax (a>0) x 2 + y 2 = a x ( a > 0 )
极坐标换元,得到 r 2 ≤ a ⋅ r cos θ r^2 \le a \cdot r \cos \theta r 2 ≤ a ⋅ r cos θ r ≤ a cos θ r \le a \cos\theta r ≤ a cos θ
然后
S = ∬ D 1 + z x 2 + z y 2 d σ = ∫ − π 2 π 2 d θ ∫ 0 a cos θ 1 + r 2 a 2 − r 2 ⋅ r d r = 1 2 ∫ − π 2 π 2 ( − 2 a a 2 − t ) ∣ 0 a 2 cos 2 θ d θ = 1 2 ∫ − π 2 π 2 2 a 2 ( 1 − ∣ sin θ ∣ ) d θ = a 2 ( π − 2 ) S=\iint_D \sqrt{1+z_x^2+z_y^2} \mathrm d \sigma=\int_{-\frac{\pi}{2}}^\frac{\pi}{2} \mathrm d \theta \int_0^{a\cos \theta}\sqrt{1+\frac{r^2}{a^2-r^2}} \cdot r\mathrm d r\\
=\frac{1}{2} \int_{-\frac{\pi}{2}}^\frac{\pi}{2} \left.\left(-2a\sqrt{a^2-t}\right)\right|_0^{a^2 \cos^2\theta} \mathrm d \theta=\frac{1}{2}\int_{-\frac{\pi}{2}} ^\frac{\pi}{2} 2a^2(1-{\color{red}|\sin\theta\,|})\mathrm d \theta=a^2(\pi-2)
S = ∬ D 1 + z x 2 + z y 2 d σ = ∫ − 2 π 2 π d θ ∫ 0 a cos θ 1 + a 2 − r 2 r 2 ⋅ r d r = 2 1 ∫ − 2 π 2 π ( − 2 a a 2 − t ) ∣ ∣ ∣ 0 a 2 cos 2 θ d θ = 2 1 ∫ − 2 π 2 π 2 a 2 ( 1 − ∣ sin θ ∣ ) d θ = a 2 ( π − 2 )

2 π 3 ( 2 2 − 1 ) \frac{2\pi}{3}(2\sqrt{2}-1)
3 2 π ( 2 2 − 1 )
设 B ( r ) = { ( x , y ) ∈ R n ∣ x 2 + y 2 ≤ r 2 } B(r)=\{(x,y)\in\R^n \mid x^2+y^2 \le r^2 \} B ( r ) = { ( x , y ) ∈ R n ∣ x 2 + y 2 ≤ r 2 }
F ( r ) = ∬ B ( r ) ( e x 2 + y 2 − a y 2 ) d σ F(r)=\iint_{B(r)} \left(e^{x^2+y^2}-ay^2\right)\mathrm d \sigma
F ( r ) = ∬ B ( r ) ( e x 2 + y 2 − a y 2 ) d σ
在 r ∈ ( 0 , + ∞ ) r\in(0,+\infin) r ∈ ( 0 , + ∞ ) a a a a a a
应该是对称的形式,转化为:
F ( r ) = ∬ B ( r ) ( e x 2 + y 2 − a ( x 2 + y 2 ) / 2 ) d σ F(r)=\iint_{B(r)} \left(e^{x^2+y^2}-a(x^2+y^2)/2\right)\mathrm d \sigma
F ( r ) = ∬ B ( r ) ( e x 2 + y 2 − a ( x 2 + y 2 ) / 2 ) d σ
然后得到 a ≤ 2 e a\le 2e a ≤ 2 e


交换积分次序。
空间立体 Ω = { ( x , y , z ) ∣ x 2 ≤ z ≤ 1 , y 2 ≤ z ≤ 1 } \Omega=\{(x,y,z) \mid x^2 \le z \le 1 , y^2 \le z \le 1\} Ω = { ( x , y , z ) ∣ x 2 ≤ z ≤ 1 , y 2 ≤ z ≤ 1 } V = V= V =
应该是对称的吧,计算区域
D = { 0 ≤ x ≤ 1 , 0 ≤ y ≤ x } D=\{0 \le x \le 1, 0 \le y \le x\}
D = { 0 ≤ x ≤ 1 , 0 ≤ y ≤ x }
对应的体积。这里,要求 x 2 ≤ z ≤ 1 x^2 \le z \le 1 x 2 ≤ z ≤ 1
V = 8 ∫ 0 1 d x ∫ 0 x d y ∫ x 2 1 d z = 2 V=8\int_0^1 \mathrm d x \int_0^x \mathrm d y \int_{x^2} ^1 \mathrm d z=2
V = 8 ∫ 0 1 d x ∫ 0 x d y ∫ x 2 1 d z = 2
设奇函数 f ( x ) f(x) f ( x ) R \R R D D D r 2 = cos 2 θ r^2 = \cos 2 \theta r 2 = cos 2 θ
I 1 = ∬ D ( f ( x ) + f ( y ) ) d σ I 2 = ∬ D f ( x + y ) d σ I_1=\iint_D (f(x)+f(y)) \mathrm d \sigma \quad I_2=\iint_D f(x+y) \mathrm d \sigma
I 1 = ∬ D ( f ( x ) + f ( y ) ) d σ I 2 = ∬ D f ( x + y ) d σ
则……
都是 0 罢,I 1 = I 2 I_1=I_2 I 1 = I 2

简单的
∫ 0 1 d y ∫ y 2 2 − y f ( x , y ) d x \int_0^1 \mathrm d y \int_{y^2}^{2-y} f(x,y) \mathrm d x
∫ 0 1 d y ∫ y 2 2 − y f ( x , y ) d x

用一个不知道正确性的方法,首先,先泰勒展开一下
lim t → 0 + φ ( t ) = ∬ A ( t ) ( 1 + x + x 2 2 ) ( 1 − y 2 2 ) x 2 + y 2 \lim_{t \to 0^{+}} \varphi(t)=\iint_{A(t)} \frac{(1+x+\frac{x^2}{2}) (1-\frac{y^2}{2})}{x^2+y^2}
t → 0 + lim φ ( t ) = ∬ A ( t ) x 2 + y 2 ( 1 + x + 2 x 2 ) ( 1 − 2 y 2 )
利用积分区间的对称性,然后再极坐标换元,我们得到,
lim t → 0 + φ ( t ) = ∫ 0 2 π d θ ∫ t 2 t ( 1 + x 2 2 ) ( 1 − y 2 2 ) / r d r \lim_{t \to 0^{+}} \varphi(t)=\int_0^{2\pi} \mathrm d \theta \int_t^{2t} (1+\frac{x^2}{2})(1-\frac{y^2}{2})/r \mathrm d r
t → 0 + lim φ ( t ) = ∫ 0 2 π d θ ∫ t 2 t ( 1 + 2 x 2 ) ( 1 − 2 y 2 ) / r d r
注意到 + x 2 2 +\frac{x^2}{2} + 2 x 2 − y 2 2 -\frac{y^2}{2} − 2 y 2 x 2 y 2 4 \frac{x^2y^2}{4} 4 x 2 y 2 t → 0 t\to0 t → 0
lim t → 0 + φ ( t ) = 2 π ∫ t 2 t 1 / r d r = 2 π ln 2 \lim_{t \to 0^{+}} \varphi(t)=2\pi \int_t^{2t} 1/r \mathrm d r=2\pi \ln 2
t → 0 + lim φ ( t ) = 2 π ∫ t 2 t 1 / r d r = 2 π ln 2
好像是积分中值定理,注意到 $e^x \cos y $ 恒正,因此
lim t → 0 + φ ( t ) = e ξ cos η ∫ 0 2 π d θ ∫ t 2 t 1 r d r = 2 π e 0 cos ( 0 ) ⋅ ln 2 = 2 π ln 2 \lim_{t \to 0^{+}} \varphi(t) = e^\xi\cos \eta\int_0^{2\pi} \mathrm d \theta \int_t^{2t}\frac{1}{r}\mathrm d r=2\pi e^0\cos (0)\cdot \ln 2=2\pi \ln 2
t → 0 + lim φ ( t ) = e ξ cos η ∫ 0 2 π d θ ∫ t 2 t r 1 d r = 2 π e 0 cos ( 0 ) ⋅ ln 2 = 2 π ln 2
设平面区域 D = { ( x , y ) ∣ x 2 4 + y 2 ≤ 1 , x ≥ 0 , y ≥ 0 } D=\left\{(x, y) \mid \frac{x^2}{4}+y^2 \leq 1, x \geq 0, y \geq 0\right\} D = { ( x , y ) ∣ 4 x 2 + y 2 ≤ 1 , x ≥ 0 , y ≥ 0 } ∬ D ∣ x − y ∣ d σ \iint_D|x-y| \mathrm{d} \sigma ∬ D ∣ x − y ∣ d σ
广义极坐标。
设空间区域 Ω = { ( x , y , z ) ∣ x 2 + y 2 + z 2 ≤ 4 ≤ x 2 + 4 y 2 + z 2 , z ≥ 0 } \Omega=\left\{(x, y, z) \mid x^2+y^2+z^2 \leq 4 \leq x^2+4 y^2+z^2, z \geq 0\right\} Ω = { ( x , y , z ) ∣ x 2 + y 2 + z 2 ≤ 4 ≤ x 2 + 4 y 2 + z 2 , z ≥ 0 }
∭ Ω ( x 2 + y 2 ) d V \iiint_{\Omega}\left(x^2+y^2\right) \mathrm{d} V
∭ Ω ( x 2 + y 2 ) d V
分两个区域计算,先计算外面的,Ω 1 = { ( x , y , z ) ∣ x 2 + y 2 + z 2 ≤ 4 , z ≥ 0 } \Omega_1=\left\{(x, y, z) \mid x^2+y^2+z^2 \leq 4,z \geq 0\right\} Ω 1 = { ( x , y , z ) ∣ x 2 + y 2 + z 2 ≤ 4 , z ≥ 0 }
2 / 3 ∭ Ω 1 ( x 2 + y 2 + z 2 ) d V = 2 / 3 ⋅ 2 π ⋅ 32 5 = 128 15 π 2/3 \iiint_{\Omega_1}(x^2+y^2+z^2) \mathrm d V=2/3 \cdot 2\pi \cdot \frac{32}{5}=\frac{128}{15}\pi
2 / 3 ∭ Ω 1 ( x 2 + y 2 + z 2 ) d V = 2 / 3 ⋅ 2 π ⋅ 5 3 2 = 1 5 1 2 8 π
再计算里面的,换元 Y = 2 y Y=2y Y = 2 y
5 12 ∭ Ω 2 ( x 2 + Y 2 + z 2 ) 1 2 d V ′ = 8 3 π \frac{5}{12} \iiint_{\Omega_2} (x^2+Y^2+z^2) \frac{1}{2}\mathrm d V'=\frac{8}{3} \pi
1 2 5 ∭ Ω 2 ( x 2 + Y 2 + z 2 ) 2 1 d V ′ = 3 8 π
减一下发现是
88 π 15 \frac{88\pi}{15}
1 5 8 8 π
设 S S S z = x 2 + y 2 z=\sqrt{x^2+y^2} z = x 2 + y 2 x 2 + y 2 = 2 y x^2+y^2 = 2y x 2 + y 2 = 2 y S S S
还是极坐标换元,令 x = r sin θ , y = r cos θ + 1 x=r\sin\theta,y=r\cos \theta+1 x = r sin θ , y = r cos θ + 1
S = ∫ 0 2 π d θ ∫ 0 1 1 + 1 r d r S=\int_0^{2\pi}\mathrm d \theta \int_0^ 1 \sqrt{1+1} r\mathrm d r
S = ∫ 0 2 π d θ ∫ 0 1 1 + 1 r d r
简单的,2 π \sqrt{2}\pi 2 π x o y xoy x o y θ \theta θ 1 / cos θ 1/\cos \theta 1 / cos θ

A,简单的。
∫ 0 2 d x ∫ x 2 e − y 2 d y \int_0^2 \mathrm d x\int_x^2 e^{-y^2} \mathrm d y
∫ 0 2 d x ∫ x 2 e − y 2 d y
经典交换积分变量,得到
∫ 0 2 d y ∫ 0 y e − y 2 d x = 1 2 ( 1 − e − 4 ) \int_0^2 \mathrm d y\int_0^y e^{-y^2} \mathrm d x=\frac{1}{2} (1-e^{-4})
∫ 0 2 d y ∫ 0 y e − y 2 d x = 2 1 ( 1 − e − 4 )
设平面区域 D D D y = x , y = x + 2 π , x = 0 y=x,y=x+2\pi,x=0 y = x , y = x + 2 π , x = 0 x = π x=\pi x = π
∬ D ∣ cos ( x − y ) ∣ d σ \iint_D |\cos (x-y)\, | \mathrm d \sigma
∬ D ∣ cos ( x − y ) ∣ d σ
一眼换元。
就是
∫ 0 π d u ∫ 0 2 π ∣ cos v ∣ d v = 4 π \int_0^\pi \mathrm d u\int_0^{2\pi} |\cos v\, |\mathrm d v=4\pi
∫ 0 π d u ∫ 0 2 π ∣ cos v ∣ d v = 4 π
计算二重积分 ∬ D x y f ′ ′ ( x 2 + y 2 ) d σ \displaystyle \iint_D xy f''(x^2+y^2) \mathrm d \sigma ∬ D x y f ′ ′ ( x 2 + y 2 ) d σ D = { ( x , y ) ∣ x 2 + y 2 ≤ 1 , x ≥ 0 , y ≥ 0 } D=\{(x,y) \mid x^2+y^2 \le 1, x\ge 0,y\ge 0\} D = { ( x , y ) ∣ x 2 + y 2 ≤ 1 , x ≥ 0 , y ≥ 0 } f ( u ) f(u) f ( u ) [ 0 , 1 ] [0,1] [ 0 , 1 ]
极坐标换元+分部积分 ,一元微积分忘光光力。
答案是
1 4 ( f ′ ( 1 ) − f ( 1 ) + f ( 0 ) ) \frac{1}{4} (f'(1)-f(1)+f(0))
4 1 ( f ′ ( 1 ) − f ( 1 ) + f ( 0 ) )

柱面坐标。

是它旋转。
设函数 f ( x ) f(x) f ( x ) F ( t ) = ∭ Ω f ( x 2 + y 2 + z 2 ) d V ∬ D f ( x 2 + y 2 ) d σ \displaystyle F(t)=\frac{\iiint_{\Omega} f\left(x^2+y^2+z^2\right) \mathrm{d} V}{\iint_D f\left(x^2+y^2\right) \mathrm{d} \sigma} F ( t ) = ∬ D f ( x 2 + y 2 ) d σ ∭ Ω f ( x 2 + y 2 + z 2 ) d V Ω = { ( x , y , z ) ∣ x 2 + y 2 + z 2 ≤ t 2 } , D = { ( x , y ) ∣ x 2 + y 2 ≤ t 2 } \Omega=\left\{(x, y, z) \mid x^2+y^2+z^2 \leq t^2\right\}, D=\left\{(x, y) \mid x^2+y^2 \leq t^2\right\} Ω = { ( x , y , z ) ∣ x 2 + y 2 + z 2 ≤ t 2 } , D = { ( x , y ) ∣ x 2 + y 2 ≤ t 2 } F ( t ) F(t) F ( t ) ( 0 , + ∞ ) (0,+\infty) ( 0 , + ∞ )
极坐标换元、球面换元得到
F ( t ) = 2 ∫ 0 t f ( r 2 ) r 2 d r ∫ 0 t f ( r 2 ) r d r F(t)=2\frac{\int_0^t f(r^2) r^2 \mathrm d r}{\int_0^t f(r^2) r \mathrm d r}
F ( t ) = 2 ∫ 0 t f ( r 2 ) r d r ∫ 0 t f ( r 2 ) r 2 d r
这个东西还是要换元处理
F ( t ) = 2 ∫ 0 t g ( r ) r d r ∫ 0 t g ( r ) d r F(t)=2\frac{\int_0^t g(r) r\mathrm d r}{\int_0^t g(r)\mathrm d r}
F ( t ) = 2 ∫ 0 t g ( r ) d r ∫ 0 t g ( r ) r d r
F ′ ( t ) F'(t) F ′ ( t )
g ( t ) t ∫ 0 t g ( r ) d r − g ( t ) ∫ 0 t g ( r ) r d r g(t)t\int_0^t g(r)\mathrm d r-g(t)\int_0^t g(r)r\mathrm d r
g ( t ) t ∫ 0 t g ( r ) d r − g ( t ) ∫ 0 t g ( r ) r d r
相同,再化一下,得到
g ( t ) ∫ 0 t ( t − r ) g ( r ) d r = f ( t 2 ) t ∫ 0 t ( t − r ) f ( r 2 ) r d r g(t)\int_0^t (t-r)g(r)\mathrm d r=f(t^2)t\int_0^t (t-r) f(r^2)r\mathrm d r
g ( t ) ∫ 0 t ( t − r ) g ( r ) d r = f ( t 2 ) t ∫ 0 t ( t − r ) f ( r 2 ) r d r
显然为正,因此 F ( t ) F(t) F ( t )
已知平面薄板所占的区域 D D D y = x 2 y=x^2 y = x 2 y = x y=x y = x ρ ( x , y ) = x 2 y \rho(x,y)=x^2 y ρ ( x , y ) = x 2 y
算呗……
M = ∫ 0 1 d x ∫ x 2 x x 2 y d y = 1 35 M=\int_0^1 \mathrm d x\int_{x^2}^x x^2 y \mathrm d y=\frac{1}{35}
M = ∫ 0 1 d x ∫ x 2 x x 2 y d y = 3 5 1
M x = ∫ 0 1 d x ∫ x 2 x x 3 y d y = 1 48 M_x=\int_0^1 \mathrm d x\int_{x^2}^x x^3 y \mathrm d y=\frac{1}{48}
M x = ∫ 0 1 d x ∫ x 2 x x 3 y d y = 4 8 1
M y = ∫ 0 1 d y ∫ x 2 x x 2 y 2 d y = 1 54 M_y=\int_0^1 \mathrm d y\int_{x^2}^x x^2 y^2 \mathrm d y=\frac{1}{54}
M y = ∫ 0 1 d y ∫ x 2 x x 2 y 2 d y = 5 4 1
所以质心坐标 ( 35 48 , 35 54 ) (\frac{35}{48},\frac{35}{54}) ( 4 8 3 5 , 5 4 3 5 )


需要注意积分区域。先利用对称性化简。

积分:
∫ x 2 + a 2 d x = 1 2 ( x x 2 + a 2 + a 2 ln ( a 2 + x 2 + x ) ) \int\sqrt{x^2+a^2} \mathrm d x=\frac{1}{2}\left(x\sqrt{x^2+a^2}+a^2 \ln(\sqrt{a^2+x^2}+x)\right)
∫ x 2 + a 2 d x = 2 1 ( x x 2 + a 2 + a 2 ln ( a 2 + x 2 + x ) )

换元代入表达式。画图比较难以看出。
计算极限
lim n → + ∞ ∑ i = 1 n ∑ j = 1 n n ( n + i ) ( n 2 + 2 j 2 ) \lim_{n \to + \infin} \sum_{i=1}^n \sum_{j=1}^n \frac{n}{(n+i)(n^2+2j^2)}
n → + ∞ lim i = 1 ∑ n j = 1 ∑ n ( n + i ) ( n 2 + 2 j 2 ) n
转化为:
lim n → + ∞ 1 n ∑ i = 1 n 1 n ∑ j = 1 n 1 ( 1 + i n ) ( 1 + 2 ( j n ) 2 ) = ∫ 0 1 d x ∫ 0 1 1 ( 1 + x ) ( 1 + 2 y 2 ) d y = ∫ 0 1 1 1 + x × ( 2 2 arctan 2 y ) ∣ 0 1 d x = 2 2 ln 2 ⋅ arctan 2 \lim_{n \to +\infin} \frac{1}{n} \sum_{i=1}^n \frac{1}{n} \sum_{j=1}^n \frac{1}{(1+\frac{i}{n})(1+2(\frac{j}{n})^2)}\\
=\int_0^1 \mathrm d x \int_0^1 \frac{1}{(1+x)(1+2y^2)} \mathrm d y\\
=\int_0^1 \frac{1}{1+x} \times \left.\left(\frac{\sqrt{2}}{2} \arctan \sqrt 2 y\right)\right |_0^1\mathrm d x=\frac{\sqrt{2}}{2} \ln 2 \cdot \arctan \sqrt{2}
n → + ∞ lim n 1 i = 1 ∑ n n 1 j = 1 ∑ n ( 1 + n i ) ( 1 + 2 ( n j ) 2 ) 1 = ∫ 0 1 d x ∫ 0 1 ( 1 + x ) ( 1 + 2 y 2 ) 1 d y = ∫ 0 1 1 + x 1 × ( 2 2 arctan 2 y ) ∣ ∣ ∣ ∣ ∣ 0 1 d x = 2 2 ln 2 ⋅ arctan 2
设函数
F ( t ) = ∬ D ( t ) ( 1 2 sin 2 x + y 2 ) d x d y F(t)=\iint_{D(t)} \left(\frac{1}{2} \sin^2 x + y^2 \right) \mathrm d x \mathrm d y
F ( t ) = ∬ D ( t ) ( 2 1 sin 2 x + y 2 ) d x d y
其中
D ( t ) = { ( x , y ) ∣ ∣ x ∣ ≤ 2 t , ∣ y ∣ ≤ 3 } ( t > 0 ) D(t)=\{(x,y) \mid |x | \le 2t, |y| \le 3\} \quad(t>0)
D ( t ) = { ( x , y ) ∣ ∣ x ∣ ≤ 2 t , ∣ y ∣ ≤ 3 } ( t > 0 )
求 F ′ ( t ) F'(t) F ′ ( t )
利用好变上限函数。原式转化为
∫ − 2 t 2 t ( 3 sin 2 x + 18 ) d x \int_{-2t}^{2t} (3 \sin^2 x +18) \mathrm d x
∫ − 2 t 2 t ( 3 sin 2 x + 1 8 ) d x
因此
F ′ ( t ) = 2 ( 3 sin 2 2 t + 18 ) − ( − 2 ) ( 3 sin 2 ( − 2 t ) + 18 ) = 12 sin 2 ( 2 t ) + 72 F'(t)=2(3\sin^2 2t+18)-(-2)(3 \sin^2 (-2t)+18)=12 \sin^2 (2t)+72
F ′ ( t ) = 2 ( 3 sin 2 2 t + 1 8 ) − ( − 2 ) ( 3 sin 2 ( − 2 t ) + 1 8 ) = 1 2 sin 2 ( 2 t ) + 7 2

换元即可。答案是 2 + 2 ln 2 2+2\ln2 2 + 2 ln 2

考察广义极坐标,
∫ 0 2 π d θ ∫ 0 1 f ( 2 r cos θ , 3 r sin θ ) 6 r ⋅ d r \int_0^{2\pi} \mathrm d \theta \int_0^1 f(2r \cos\theta,3r\sin\theta)6r\cdot \mathrm d r
∫ 0 2 π d θ ∫ 0 1 f ( 2 r cos θ , 3 r sin θ ) 6 r ⋅ d r
求曲面 x 2 + y 2 = 4 z ( z ≤ 2 ) x^2+y^2 =4z\ (z\le 2) x 2 + y 2 = 4 z ( z ≤ 2 ) x 2 + y 2 ≤ 8 x^2+y^2 \le 8 x 2 + y 2 ≤ 8 2 3 π ( 3 3 − 1 ) \frac{2}{3}\pi (3\sqrt{3}-1) 3 2 π ( 3 3 − 1 ) y = f ( x ) y=f(x) y = f ( x ) y y y y = f ( x 2 + z 2 ) y=f(\sqrt{x^2+z^2}) y = f ( x 2 + z 2 )
记 D = { ( x , y ) ∣ x 2 + y 2 ≤ 1 } D=\{(x,y) \mid x^2 + y^2 \le 1\} D = { ( x , y ) ∣ x 2 + y 2 ≤ 1 }
∬ D ( sin x 2 cos y 2 + x e x 2 + y 2 ) d x d y \iint_D (\sin x^2 \cos y^2 + x e^{x^2+y^2}) \mathrm d x\mathrm d y
∬ D ( sin x 2 cos y 2 + x e x 2 + y 2 ) d x d y
首先,找出对称的部分,转化为:
∬ D sin x 2 cos y 2 d x d y \iint_D \sin x^2 \cos y^2 \mathrm d x \mathrm d y
∬ D sin x 2 cos y 2 d x d y
发现 x , y x,y x , y
1 2 ∬ D sin ( x 2 + y 2 ) d x d y = 1 2 ∫ 0 2 π d θ ∫ 0 1 r sin r 2 d r = π sin 2 ( 1 2 ) \frac{1}{2}\iint_D \sin (x^2+y^2) \mathrm d x \mathrm d y= \frac{1}{2} \int_0^{2\pi} \mathrm d \theta \int_0^1 r \sin r^2 \mathrm d r=\pi \sin^2 \left(\frac{1}{2}\right)
2 1 ∬ D sin ( x 2 + y 2 ) d x d y = 2 1 ∫ 0 2 π d θ ∫ 0 1 r sin r 2 d r = π sin 2 ( 2 1 )
注:类似于 e x 2 e^{x^2} e x 2
已知函数 f ( x ) f(x) f ( x ) ∫ − 1 1 x f ( x ) d x = 2 π \displaystyle \int_{-1}^1 xf(x)\mathrm d x=2\pi ∫ − 1 1 x f ( x ) d x = 2 π Ω \Omega Ω
∭ Ω ( 3 x 2 + f ′ ( z ) + 1 ) d V \iiint_{\Omega} (3x^2+f'(z)+1)\mathrm d V
∭ Ω ( 3 x 2 + f ′ ( z ) + 1 ) d V
知识点:球面坐标、柱面坐标、轮换对称性。注意不能光用同一种坐标。
对于 ∭ Ω ( x 2 + y 2 + z 2 + 1 ) d V \displaystyle \iiint _{\Omega} (x^2+y^2+z^2+1)\mathrm d V ∭ Ω ( x 2 + y 2 + z 2 + 1 ) d V 32 15 π \frac{32}{15}\pi 1 5 3 2 π
对于 ∭ Ω f ′ ( z ) d z \displaystyle \iiint_{\Omega} f'(z)\mathrm d z ∭ Ω f ′ ( z ) d z z z z
设二元连续函数 f ( x , y ) f(x,y) f ( x , y ) lim ( x , y ) → ( 0 , 0 ) ∫ 0 1 f ( t x , t y ) d t ⏞ F ( x , y ) x 2 + y 2 = A \displaystyle \lim_{(x,y)\to (0,0)} \frac{\overbrace{\int_0^1 f(tx,ty)\mathrm d t}^{F(x,y)}}{\sqrt{x^2+y^2}}=A ( x , y ) → ( 0 , 0 ) lim x 2 + y 2 ∫ 0 1 f ( t x , t y ) d t F ( x , y ) = A A A A f x ( 0 , 0 ) f_x(0,0) f x ( 0 , 0 ) f y ( 0 , 0 ) f_y(0,0) f y ( 0 , 0 )
要先证明 A = 0 A=0 A = 0 x = 0 x=0 x = 0
lim ( x , y ) → ( 0 , 0 ) F ( 0 , y ) ∣ x ∣ = A \lim_{(x,y) \to (0,0)} \frac{F(0,y)}{|x|}=A
( x , y ) → ( 0 , 0 ) lim ∣ x ∣ F ( 0 , y ) = A
然后 A = 0 A=0 A = 0

简单的。

注意是高斯函数平方。

球坐标代换,计算有点烦。
计算三重积分 I = ∭ Ω x sin ( y + z ) d x d y d z \displaystyle I=\iiint_\Omega x \sin (y+z)\mathrm d x\mathrm d y\mathrm d z I = ∭ Ω x sin ( y + z ) d x d y d z Ω \Omega Ω x = 0 , z = 0 , y + x = π 2 x=0,z=0,y+x=\frac{\pi}{2} x = 0 , z = 0 , y + x = 2 π x = y x=\sqrt{y} x = y


比较简单。




注意球面坐标上下限的含义。

用柱面坐标更简单。


其实容易发现上面和下面都是椭圆。圆锥曲线的定义。
然后极坐标换元计算侧面积:
∫ 0 2 π d θ ∫ 0 3 [ 4 − 4 sin θ ] ⋅ 3 d r = 24 π \int_0^{2\pi} \mathrm d \theta \int_0^3 [4-4\sin\theta] \cdot 3 \mathrm d r=24\pi
∫ 0 2 π d θ ∫ 0 3 [ 4 − 4 sin θ ] ⋅ 3 d r = 2 4 π

对称性,形心 y y y x x x
设在 D = [ a , b ] × [ c , d ] D=[a,b] \times [c,d] D = [ a , b ] × [ c , d ] f ( x , y ) f(x,y) f ( x , y )
证明
∬ D f x y ′ ′ ( x , y ) d x d y = ∬ D f y x ′ ′ ( x , y ) d x d y \iint_D f''_{xy} (x,y) \mathrm d x\mathrm d y = \iint_D f''_{yx}(x,y) \mathrm d x \mathrm d y
∬ D f x y ′ ′ ( x , y ) d x d y = ∬ D f y x ′ ′ ( x , y ) d x d y
都等于
f ( b , d ) + f ( a , c ) − f ( a , d ) − f ( b , c ) f(b,d)+f(a,c) - f(a,d)-f(b,c)
f ( b , d ) + f ( a , c ) − f ( a , d ) − f ( b , c )
利用题 ( 1 ) (1) ( 1 ) ∀ ( x , y ) ∈ D \forall (x,y) \in D ∀ ( x , y ) ∈ D f x y ′ ′ ( x , y ) = f y x ′ ′ ( x , y ) f''_{xy}(x,y) = f''_{yx}(x,y) f x y ′ ′ ( x , y ) = f y x ′ ′ ( x , y )
有结论:
如果对于任何区域 D ′ ∈ D D' \in D D ′ ∈ D
∬ D ′ f ( x , y ) d x d y = 0 \iint_{D'} f(x,y)\mathrm d x\mathrm d y=0
∬ D ′ f ( x , y ) d x d y = 0
且 f ( x , y ) f(x,y) f ( x , y ) f ( x , y ) ≡ 0 f(x,y)\equiv 0 f ( x , y ) ≡ 0
设函数 f ( x ) f(x) f ( x ) [ a , b ] [a,b] [ a , b ] f ( x ) > 0 f(x)>0 f ( x ) > 0
∫ a b f ( x ) e f ( x ) d x ∫ a b 1 f ( x ) d x ≥ ( b − a ) [ ( b − a ) + ∫ a b f ( x ) d x ] \int_a^b f(x) e^{f(x)}\mathrm d x \int_a^b \frac{1}{f(x)}\mathrm d x \ge (b-a)\left[(b-a) + \int_a^b f(x) \mathrm d x\right]
∫ a b f ( x ) e f ( x ) d x ∫ a b f ( x ) 1 d x ≥ ( b − a ) [ ( b − a ) + ∫ a b f ( x ) d x ]
设
F ( b ) = ∫ a b f ( x ) e f ( x ) d x ∫ a b 1 f ( x ) d x − ( b − a ) [ ( b − a ) + ∫ a b f ( x ) d x ] F(b)=\int_a^b f(x) e^{f(x)}\mathrm d x \int_a^b \frac{1}{f(x)}\mathrm d x - (b-a)\left[(b-a) + \int_a^b f(x) \mathrm d x\right]
F ( b ) = ∫ a b f ( x ) e f ( x ) d x ∫ a b f ( x ) 1 d x − ( b − a ) [ ( b − a ) + ∫ a b f ( x ) d x ]
则
d F ( b ) d b = f ( b ) e f ( b ) ∫ a b 1 f ( x ) d x + 1 f ( b ) ∫ a b f ( x ) e f ( x ) d x − [ ( b − a ) + ∫ a b f ( x ) d x ] − ( b − a ) [ 1 + f ( b ) ] \frac{\mathrm d F(b)}{\mathrm d b}=f(b)e^{f(b)} \int_a^b \frac{1}{f(x)}\mathrm d x+\frac{1}{f(b)} \int_a^b f(x)e^{f(x)}\mathrm d x-\left[(b-a) + \int_a^b f(x) \mathrm d x\right]-(b-a)[1+f(b)]
d b d F ( b ) = f ( b ) e f ( b ) ∫ a b f ( x ) 1 d x + f ( b ) 1 ∫ a b f ( x ) e f ( x ) d x − [ ( b − a ) + ∫ a b f ( x ) d x ] − ( b − a ) [ 1 + f ( b ) ]
画两个一次积分为二次积分:
L H S = ∫ a b f ( x ) e f ( x ) d x ∫ a b 1 f ( y ) d y = ∬ D f ( x ) f ( y ) e f ( x ) d σ = 1 2 ∬ D ( f ( x ) f ( y ) e f ( x ) + f ( y ) f ( x ) e f ( y ) ) d σ ⏟ 进 行 对 称 , 二 重 积 分 的 特 性 ≥ ∬ D ( e ( f ( x ) + f ( y ) ) / 2 ) d σ ≥ ∬ D ( 1 + f ( x ) + f ( y ) 2 ) d σ = ⋯ \mathrm{LHS}=\int_a^b f(x) e^{f(x)} \mathrm d x \int_a^b \frac{1}{f(y)}\mathrm d y=\iint_D \frac{f(x)}{f(y)} e^{f(x)}\mathrm d \sigma=\underbrace{\frac{1}{2}\iint_D \left(\frac{f(x)}{f(y)} e^{f(x)}+\frac{f(y)}{f(x)} e^{f(y)}\right)\mathrm d \sigma}_{进行对称,二重积分的特性}\\
\ge \iint_D \left(e^{(f(x)+f(y))/2}\right)\mathrm d \sigma\ge \iint_D \left(1+\frac{f(x)+f(y)}{2}\right)\mathrm d \sigma = \cdots
L H S = ∫ a b f ( x ) e f ( x ) d x ∫ a b f ( y ) 1 d y = ∬ D f ( y ) f ( x ) e f ( x ) d σ = 进 行 对 称 , 二 重 积 分 的 特 性 2 1 ∬ D ( f ( y ) f ( x ) e f ( x ) + f ( x ) f ( y ) e f ( y ) ) d σ ≥ ∬ D ( e ( f ( x ) + f ( y ) ) / 2 ) d σ ≥ ∬ D ( 1 + 2 f ( x ) + f ( y ) ) d σ = ⋯
因此,利用二重积分的特性,可以将 x , y x,y x , y 轮换式 ,因此好比较大小。
设 D = [ a , b ] × [ a , b ] D=[a,b] \times [a,b] D = [ a , b ] × [ a , b ] f ( x ) f(x) f ( x ) [ a , b ] [a,b] [ a , b ]
∬ D y f ( y ) d x d y ≥ b 2 − a 2 2 ∫ a b f ( x ) d x \iint_D yf(y) \mathrm d x\mathrm d y \ge \frac{b^2-a^2}{2} \int_a^b f(x)\mathrm d x
∬ D y f ( y ) d x d y ≥ 2 b 2 − a 2 ∫ a b f ( x ) d x
需要注意到
b 2 − a 2 2 = ∫ a b y d y \frac{b^2-a^2}{2} = \int_a^b y \mathrm d y
2 b 2 − a 2 = ∫ a b y d y
b 2 − a 2 2 ∫ a b f ( x ) d x = ∫ a b y d y ∫ a b f ( x ) d x = ∬ D y f ( x ) d x d y \frac{b^2-a^2}{2} \int_a^b f(x)\mathrm d x=\int_a^b y \mathrm d y\int_a^b f(x)\mathrm d x=\iint_D yf(x)\mathrm d x \mathrm d y
2 b 2 − a 2 ∫ a b f ( x ) d x = ∫ a b y d y ∫ a b f ( x ) d x = ∬ D y f ( x ) d x d y
转化为
∬ D y ( f ( y ) − f ( x ) ) d x d y ≥ 0 \iint_D y (f(y)-f(x))\mathrm d x \mathrm d y \ge 0
∬ D y ( f ( y ) − f ( x ) ) d x d y ≥ 0
又等于
1 2 ∬ D ( y − x ) ( f ( y ) − f ( x ) ) d x d y \frac{1}{2} \iint_D (y-x) (f(y)-f(x))\mathrm d x \mathrm d y
2 1 ∬ D ( y − x ) ( f ( y ) − f ( x ) ) d x d y
设 f ( x , y ) f(x,y) f ( x , y )
f ( 0 , 0 ) = lim ε → 0 − 1 2 π ∬ ε 2 ≤ x 2 + y 2 ≤ 1 x f x + y f y x 2 + y 2 d x d y f(0,0)=\lim_{\varepsilon \to 0}\frac{-1}{2\pi} \iint_{\varepsilon^2 \le x^2+y^2\le 1} \frac{xf_x+yf_y}{x^2+y^2}\mathrm d x\mathrm d y
f ( 0 , 0 ) = ε → 0 lim 2 π − 1 ∬ ε 2 ≤ x 2 + y 2 ≤ 1 x 2 + y 2 x f x + y f y d x d y
首先,化二重积分为二次积分。应该采用极坐标。
∫ 0 2 π d θ ∫ ∣ ε ∣ 1 r cos θ f x + r sin θ f y r 2 r d r = ∫ 0 2 π d θ ∫ ∣ ε ∣ 1 ( cos θ f x + sin θ f y ) d r \int_0^{2\pi} \mathrm d \theta \int_{|\varepsilon|} ^ 1 \frac{r \cos \theta f_x+ r \sin \theta f_y}{r^2} r\mathrm d r
=\int_0^{2\pi}\mathrm d \theta \int_{|\varepsilon|}^1 (\cos\theta f_x+\sin\theta f_y) \mathrm d r
∫ 0 2 π d θ ∫ ∣ ε ∣ 1 r 2 r cos θ f x + r sin θ f y r d r = ∫ 0 2 π d θ ∫ ∣ ε ∣ 1 ( cos θ f x + sin θ f y ) d r
注意到
cos θ f x + sin θ f y = ∂ f ( r cos θ , r sin θ ) ∂ r \cos\theta f_x+\sin\theta f_y=\frac{\partial f(r\cos\theta,r\sin\theta)}{\partial r}
cos θ f x + sin θ f y = ∂ r ∂ f ( r cos θ , r sin θ )
因此,原式化为:
∫ 0 2 π ( f ( cos θ , sin θ ) − f ( ∣ ε ∣ cos θ , ∣ ε ∣ sin θ ) ) d θ \int_0^{2\pi} (f(\cos \theta,\sin\theta)-f(|\varepsilon| \cos \theta,|\varepsilon| \sin\theta)) \mathrm d \theta
∫ 0 2 π ( f ( cos θ , sin θ ) − f ( ∣ ε ∣ cos θ , ∣ ε ∣ sin θ ) ) d θ
由于在单位圆上取值为 0 0 0
f ( 0 , 0 ) = lim ε → 0 1 2 π ∫ 0 2 π f ( ∣ ε ∣ cos θ , ∣ ε ∣ sin θ ) d θ f(0,0)=\lim_{\varepsilon\to0}\frac{1}{2\pi} \int_{0}^{2\pi} f(|\varepsilon|\cos\theta,|\varepsilon| \sin\theta) \mathrm d \theta
f ( 0 , 0 ) = ε → 0 lim 2 π 1 ∫ 0 2 π f ( ∣ ε ∣ cos θ , ∣ ε ∣ sin θ ) d θ
由 积分中值定理 和 f ( x , y ) f(x,y) f ( x , y )
lim ε → 0 1 2 π f ( ∣ ε ∣ cos ξ , ∣ ε ∣ sin ξ ) = f ( 0 , 0 ) \lim_{\varepsilon \to 0}\frac{1}{2\pi} f(|\varepsilon|\cos \xi,|\varepsilon| \sin\xi)=f(0,0)
ε → 0 lim 2 π 1 f ( ∣ ε ∣ cos ξ , ∣ ε ∣ sin ξ ) = f ( 0 , 0 )

同。
证明抛物面 z = x 2 + y 2 + 1 z=x^2+y^2+1 z = x 2 + y 2 + 1 z = x 2 + y 2 z=x^2+y^2 z = x 2 + y 2 Ω \Omega Ω
设切于 ( x 0 , y 0 , z 0 ) (x_0,y_0,z_0) ( x 0 , y 0 , z 0 )
2 x 0 ( x − x 0 ) + 2 y 0 ( y − y 0 ) − ( z − z 0 ) = 0 ⇒ 2 x 0 x + 2 y 0 y − z = − z 0 + 2 ( z 0 − 1 ) 2x_0(x-x_0)+2y_0(y-y_0)-(z-z_0)=0 \Rightarrow 2x_0x+2y_0y-z=-z_0+2(z_0-1)
2 x 0 ( x − x 0 ) + 2 y 0 ( y − y 0 ) − ( z − z 0 ) = 0 ⇒ 2 x 0 x + 2 y 0 y − z = − z 0 + 2 ( z 0 − 1 )
空间区域在 x y xy x y
( x − x 0 ) 2 + ( y − y 0 ) 2 = 1 (x-x_0)^2+(y-y_0)^2=1
( x − x 0 ) 2 + ( y − y 0 ) 2 = 1
是一个圆。
因此
∣ Ω ∣ = ∬ D ( 2 x 0 x + 2 y 0 y + 2 − z 0 − x 2 − y 2 ) d x d y = 1 2 π |\Omega|=\iint_D (2x_0x+2y_0y+2-z_0-x^2-y^2) \mathrm d x\mathrm d y=\frac{1}{2} \pi
∣ Ω ∣ = ∬ D ( 2 x 0 x + 2 y 0 y + 2 − z 0 − x 2 − y 2 ) d x d y = 2 1 π
切平面以上的部分和切平面以下的部分体积相等。

设 f ( x ) f(x) f ( x )
F ( t ) = ∭ Ω [ z 2 + f ( x 2 + y 2 ) ] d x d y d z F(t)=\iiint_\Omega [z^2+f(x^2+y^2)] \mathrm d x\mathrm d y\mathrm d z
F ( t ) = ∭ Ω [ z 2 + f ( x 2 + y 2 ) ] d x d y d z
其中
Ω : 0 ≤ z ≤ h , x 2 + y 2 ≤ t 2 ( t > 0 ) \Omega : 0 \le z \le h, x^2+y^2 \le t^2 (t>0)
Ω : 0 ≤ z ≤ h , x 2 + y 2 ≤ t 2 ( t > 0 )
求 d F / d t \mathrm d F/\mathrm d t d F / d t lim t → 0 + F ( t ) / t 2 \lim_{t \to 0^+} F(t)/t^2 lim t → 0 + F ( t ) / t 2
做如下代换:x = r cos θ , y = r sin θ x=r\cos \theta,y=r\sin\theta x = r cos θ , y = r sin θ
F ( t ) = ∫ 0 h d z ∫ 0 2 π d θ ∫ 0 t [ z 2 + f ( r 2 ) ] r d r = π ∫ 0 h d z ∫ 0 t [ z 2 + f ( r 2 ) ] d r 2 = π ∫ 0 h d z ∫ 0 t 2 [ z 2 + f ( u ) ] d u F(t)=\int_0^h \mathrm d z\int_0^{2\pi}\mathrm d \theta \int_0^t [z^2+f(r^2)] r \mathrm d r\\
=\pi \int_0^h \mathrm d z \int_0^{t} [z^2 +f(r^2)]\mathrm d r^2=\pi \int_0^h \mathrm d z \int_0^{t^2} [z^2 +f(u)]\mathrm d u
F ( t ) = ∫ 0 h d z ∫ 0 2 π d θ ∫ 0 t [ z 2 + f ( r 2 ) ] r d r = π ∫ 0 h d z ∫ 0 t [ z 2 + f ( r 2 ) ] d r 2 = π ∫ 0 h d z ∫ 0 t 2 [ z 2 + f ( u ) ] d u
d F d t = 2 π t ∫ 0 h ( z 2 + f ( t 2 ) ) d z = 2 π t ( 1 3 h 3 + h f ( t 2 ) ) \frac{\mathrm d F}{\mathrm d t}=2\pi t \int_0^h (z^2+f(t^2)) \mathrm d z=2 \pi t (\frac{1}{3}h^3+hf(t^2))
d t d F = 2 π t ∫ 0 h ( z 2 + f ( t 2 ) ) d z = 2 π t ( 3 1 h 3 + h f ( t 2 ) )
lim t → 0 + F ( t ) t 2 = lim t → 0 + 2 π t ( 1 3 h 3 + h f ( t 2 ) ) 2 t = π ( 1 3 h 3 + h f ( 0 ) ) ( f ( x ) 连 续 ) \lim_{t \to 0^+} \frac{F(t)}{t^2}=\lim_{t \to 0^+}\frac{2\pi t (\frac{1}{3} h^3 +hf(t^2))}{2t}=\pi (\frac{1}{3}h^3+hf(0)) \quad(f(x) 连续)
t → 0 + lim t 2 F ( t ) = t → 0 + lim 2 t 2 π t ( 3 1 h 3 + h f ( t 2 ) ) = π ( 3 1 h 3 + h f ( 0 ) ) ( f ( x ) 连 续 )


设 f ( x ) f(x) f ( x ) [ 0 , 1 ] [0,1] [ 0 , 1 ]
∫ 0 1 d x ∫ x 1 d y ∫ x y f ( x ) f ( y ) f ( z ) d z = 1 3 ! ( ∫ 0 1 f ( t ) d t ) 3 \int_0^1 \mathrm d x\int_x^1 \mathrm d y\int_x^y f(x)f(y)f(z)\mathrm d z =\frac{1}{3!}\left(\int_0^1 f(t)\mathrm d t\right)^3
∫ 0 1 d x ∫ x 1 d y ∫ x y f ( x ) f ( y ) f ( z ) d z = 3 ! 1 ( ∫ 0 1 f ( t ) d t ) 3
轮换 6 次即可。或者,令 F ′ ( x ) = f ( x ) F'(x)=f(x) F ′ ( x ) = f ( x )
∫ 0 1 f ( x ) d x ∫ x 1 [ F ( y ) − F ( x ) ] d [ F ( y ) − F ( x ) ] ⋯ \int_0^1 f(x)\mathrm d x \int_x^1 [F(y)-F(x)]\mathrm d [F(y)-F(x)] \cdots
∫ 0 1 f ( x ) d x ∫ x 1 [ F ( y ) − F ( x ) ] d [ F ( y ) − F ( x ) ] ⋯
相似的题目:设函数 f ( x ) f(x) f ( x ) [ 0 , 1 ] [0,1] [ 0 , 1 ]
∫ 0 1 d x ∫ x 1 f ( x ) f ( y ) d y = 1 2 ( ∫ 0 1 f ( x ) d x ) 2 \int_0^1 \mathrm d x \int_x^1 f(x)f(y)\mathrm d y = \frac{1}{2} \left(\int_0^1\ f(x)\mathrm d x \right)^2
∫ 0 1 d x ∫ x 1 f ( x ) f ( y ) d y = 2 1 ( ∫ 0 1 f ( x ) d x ) 2
也就是
∫ 0 1 f ( x ) ( F ( 1 ) − F ( x ) ) d x = 1 2 ( F ( 1 ) − F ( 0 ) ) 2 \int_0^1 f(x)(F(1)-F(x)) \mathrm d x=\frac{1}{2}(F(1)-F(0))^2
∫ 0 1 f ( x ) ( F ( 1 ) − F ( x ) ) d x = 2 1 ( F ( 1 ) − F ( 0 ) ) 2
也就是
− ∫ 0 1 ( F ( 1 ) − F ( x ) ) d ( F ( 1 ) − F ( x ) ) = − ( ( F ( 1 ) − F ( x ) ) 2 2 ) ∣ 0 1 = 1 2 ( F ( 1 ) − F ( 0 ) ) 2 -\int_0^1 (F(1)-F(x)) \mathrm d(F(1)-F(x))=-\left.\left(\frac{(F(1)-F(x))^2}{2}\right)\right|_0^1=\frac{1}{2}(F(1)-F(0))^2
− ∫ 0 1 ( F ( 1 ) − F ( x ) ) d ( F ( 1 ) − F ( x ) ) = − ( 2 ( F ( 1 ) − F ( x ) ) 2 ) ∣ ∣ ∣ ∣ 0 1 = 2 1 ( F ( 1 ) − F ( 0 ) ) 2


可以先推导部分球面的面积,若底面圆的半径为 b b b
S = 2 π a ( a − a 2 − b 2 ) = 2 π a ( a − h ) = 2 π a H S=2\pi a\left(a-\sqrt{a^2-b^2}\right)=2\pi a(a-h)=2\pi a H
S = 2 π a ( a − a 2 − b 2 ) = 2 π a ( a − h ) = 2 π a H
其中 h h h
那么可以得到在这道题里面 H = R − R 2 2 a H=R-\frac{R^2}{2a} H = R − 2 a R 2 R = 4 a 3 R=\frac{4a}{3} R = 3 4 a
通过交换积分次序证明:
∫ 0 1 d x ∫ 0 x d y ∫ 0 y f ( z ) d z = 1 2 ∫ 0 1 ( 1 − z ) 2 f ( z ) d z \int_0^1 \mathrm d x\int_0^x \mathrm d y \int_0^y f(z)\mathrm d z=\frac{1}{2} \int_0^1 (1-z)^2 f(z)\mathrm d z
∫ 0 1 d x ∫ 0 x d y ∫ 0 y f ( z ) d z = 2 1 ∫ 0 1 ( 1 − z ) 2 f ( z ) d z
∫ 0 1 d x ∫ 0 x d y ∫ 0 y f ( z ) d z = ∫ 0 1 S ( D z ) f ( z ) d z = 1 2 ∫ 0 1 ( 1 − z ) 2 f ( z ) d z \int_0^1 \mathrm d x\int_0^x \mathrm d y \int_0^y f(z)\mathrm d z=\int_0^1 S(D_z)f(z)\mathrm d z=\frac{1}{2}\int_0^1 (1-z)^2 f(z)\mathrm d z
∫ 0 1 d x ∫ 0 x d y ∫ 0 y f ( z ) d z = ∫ 0 1 S ( D z ) f ( z ) d z = 2 1 ∫ 0 1 ( 1 − z ) 2 f ( z ) d z
设 B ( r ) = { ( x , y ) ∈ R 2 ∣ x 2 + y 2 ≤ r 2 } B(r)=\{(x,y)\in\R^2\mid x^2+y^2 \le r^2\} B ( r ) = { ( x , y ) ∈ R 2 ∣ x 2 + y 2 ≤ r 2 } f ( x , y ) f(x,y) f ( x , y ) 0 < f ( x , y ) < 1 0<f(x,y)<1 0 < f ( x , y ) < 1
F ( n , r ) = ( ∬ B ( r ) f n ( x , y ) d σ ) 1 n F(n,r)=\left(\iint_{B(r)} f^n(x,y)\mathrm d \sigma\right)^\frac{1}{n}
F ( n , r ) = ( ∬ B ( r ) f n ( x , y ) d σ ) n 1
求
lim n → ∞ F ( n , 1 n ) \lim_{n \to \infin} F\left(n,\frac{1}{n}\right)
n → ∞ lim F ( n , n 1 )
F ( n , 1 n ) = [ ∬ B ( 1 n ) f n ( x , y ) d σ ] 1 n = exp ln ∫ B ( 1 n ) f n ( x , y ) d σ n = exp ln f n ( ξ , η ) ∫ B ( 1 n ) d σ n F\left(n,\frac{1}{n}\right)=\left[\iint_{B(\frac{1}{n})}f^n (x,y)\mathrm d \sigma\right]^\frac{1}{n}=\exp\frac{\ln\int_{B(\frac{1}{n})}f^n(x,y)\mathrm d \sigma}{n}=\exp\frac{\ln f^n (\xi,\eta)\int_{B(\frac{1}{n})}\mathrm d \sigma}{n}
F ( n , n 1 ) = [ ∬ B ( n 1 ) f n ( x , y ) d σ ] n 1 = exp n ln ∫ B ( n 1 ) f n ( x , y ) d σ = exp n ln f n ( ξ , η ) ∫ B ( n 1 ) d σ
巧妙利用积分中值定理,得到
lim n → ∞ F ( n , 1 n ) = exp [ ln f ( 0 , 0 ) ] = f ( 0 , 0 ) \lim_{n \to \infin} F\left(n,\frac{1}{n}\right)=\exp[\ln f(0,0)]=f(0,0)
n → ∞ lim F ( n , n 1 ) = exp [ ln f ( 0 , 0 ) ] = f ( 0 , 0 )

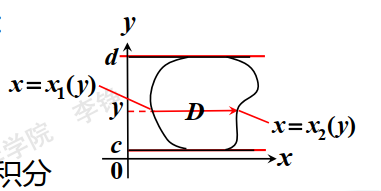





 $$
V=\underbrace{8}_{八个部分}\int_0^r (r^2-x^2)\mathrm d x
$$
$$
V=\underbrace{8}_{八个部分}\int_0^r (r^2-x^2)\mathrm d x
$$