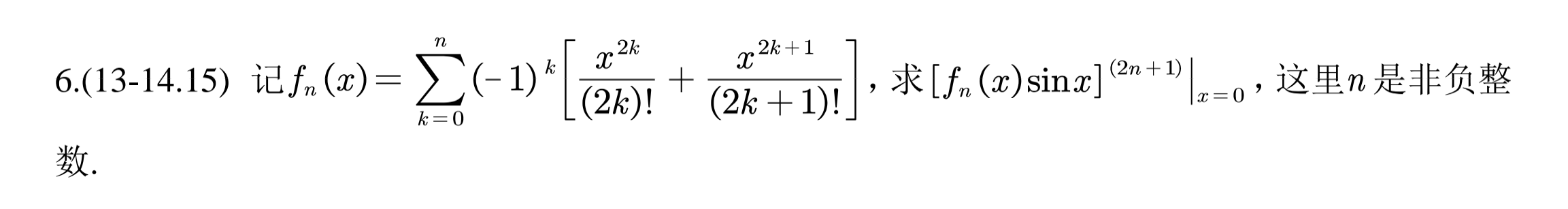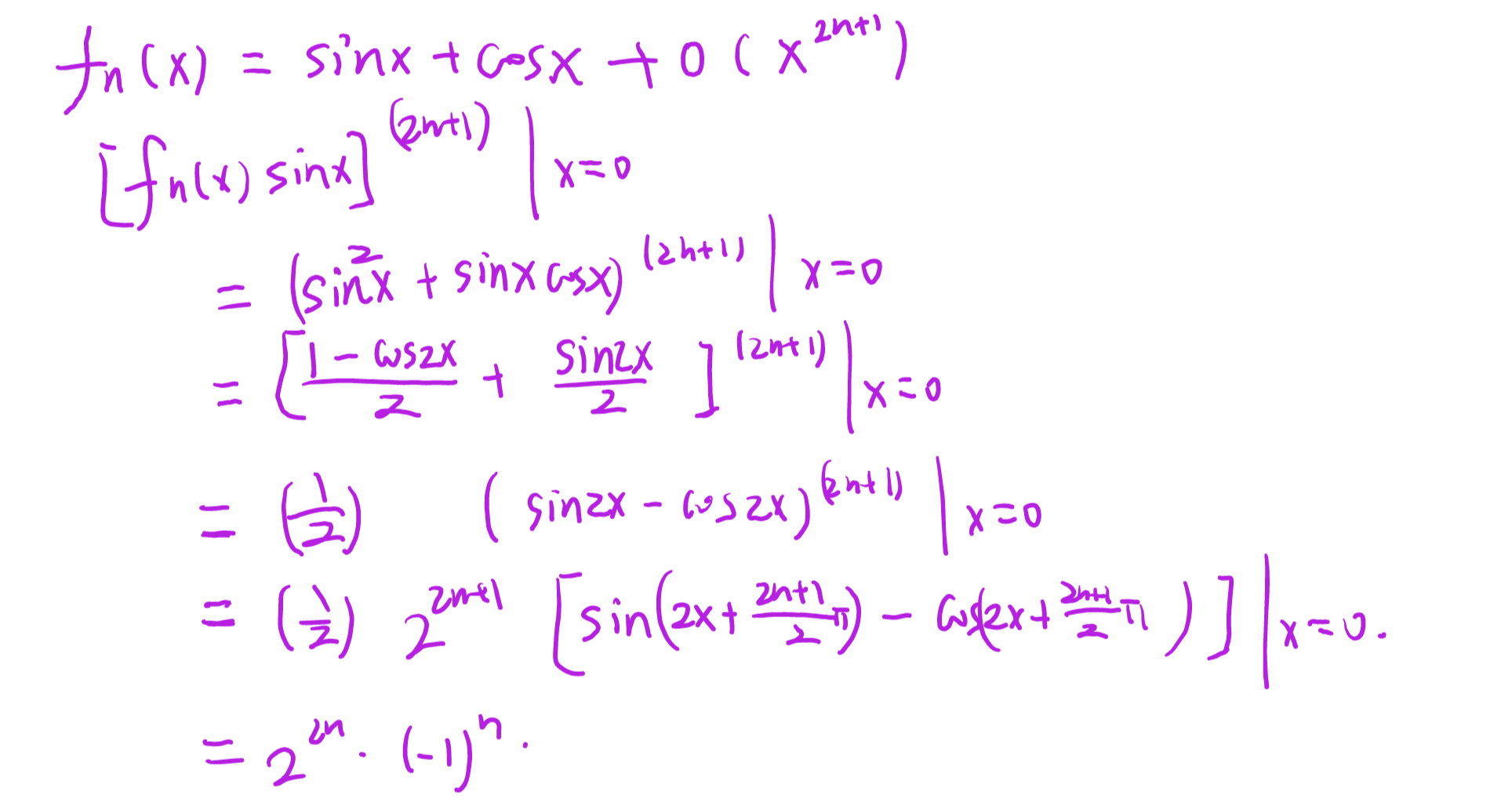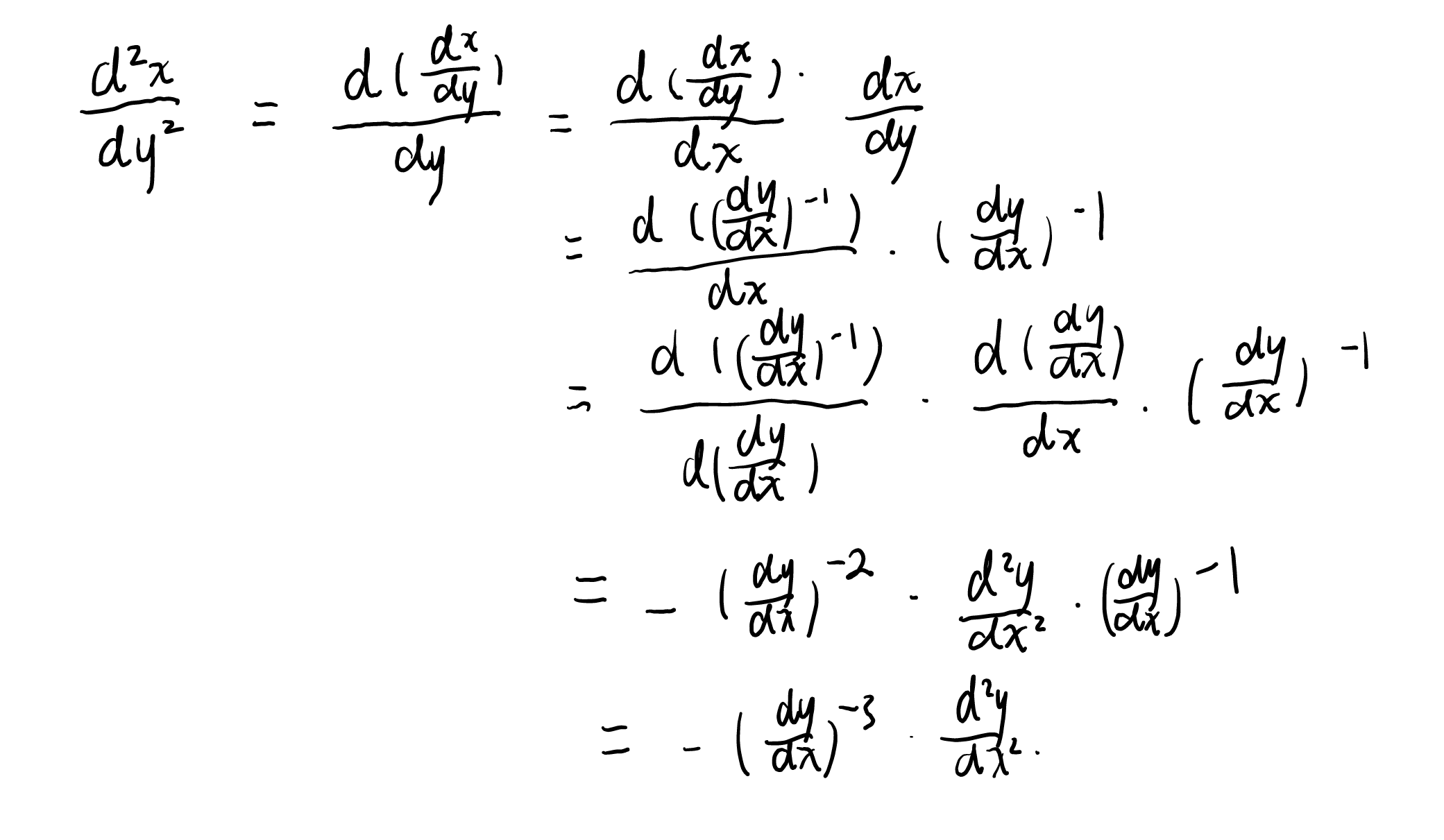高阶导数
我们经常使用数学归纳法,下面是几个常用的公式。
sin/cos(n)(x)=sin/cos(n)(x+2πn)(ax)(n)=axlnna(xa)(n)=a(a−1)⋯(a−n+1)xa−n=n!Canxa−nf(n)(ax)=anf(n)(x)
事实上,更好的是记忆一般情况:
((ax+b)α)(n)=an×⋯
对于含对数函数的情况,进行一次求导,就可以转化为一般情况:
(logα(ax+b))(n)=(alogαeln(ax+b))(n)=anlogαe(−1)n−1(n−1)!(ax+b)−n
莱布尼兹公式:
(f(x)g(x))(n)=k=0∑nCnkf(k)(x)g(n−k)(x)
可以使用数学归纳法证明,核心是杨辉三角:Cnk+Cnk+1=Cn+1k+1。
莱布尼兹公式的形式有 n 项,看似不好处理,但是如果我们合理分配 f(x),g(x),使得其中一个是有限次多项式,保证很多项为 0,就可以大大减少莱布尼兹公式的项数。
求 n 次导数需要注意的点:
- 是否单点求值,如果求单点的值,在求导的过程中合理代入,可以凑出很多 0 项,减少计算量。如果是单点求值,还可以把要求的函数转换为递推形式。
- 是否函数都有 n 阶导数,否则,不能求导次数过高。
如何更快地求出高阶导数
-
求某一点 x0 的高阶导数,最好能够凑出 (x−x0)α 的因式,因为根据莱布尼兹公式,只有求到 α 次导数的时候,这个因数的导数值才不为 0,于是就只剩下一项。
例如:f(x)=(x2−3x+2)ncos16πx2,求 f(n)(2),分解为 (x−2)n×(x−1)ncos16πx2,于是只剩下 Cnnn!((x−1)ncos16πx2)∣x=2=22n!。
-
间接求导数:我们通过两种不同的方式将 f(x) 展开,根据泰勒公式系数的唯一性,可以推知两个公式的对应系数相等,就求出了导数。
例如,求 y=ex2+2x,y(10)(−1)。
a. 泰勒公式通过定义展开:f(x)=∑k=0nk!f(k)(x0)(x−x0)k+o((x−x0)k+1)
b. 另一种展开方法。我们观察到 (x+1) 是无穷小,或者我们换元 t=(x+1),那么可以把 y 改写为 e(x+1)2/e,将 (x+1)2 看成框框,我们得到 y=e1(1+(x+1)2+2!(x+1)4+3!(x+1)6+⋯+5!(x+1)10+o((x+1)10))。另一方面,观察 y 在 (x+1)10 的系数,正是 f10(−1)/10!,那么 f10(−1)=e×5!10!。
y=x2−3x1,求 y(n)(1)。
令 t=x−1,构造出若干 1/(1−φ(t)) 即可,保证 φ(t) 是无穷小。
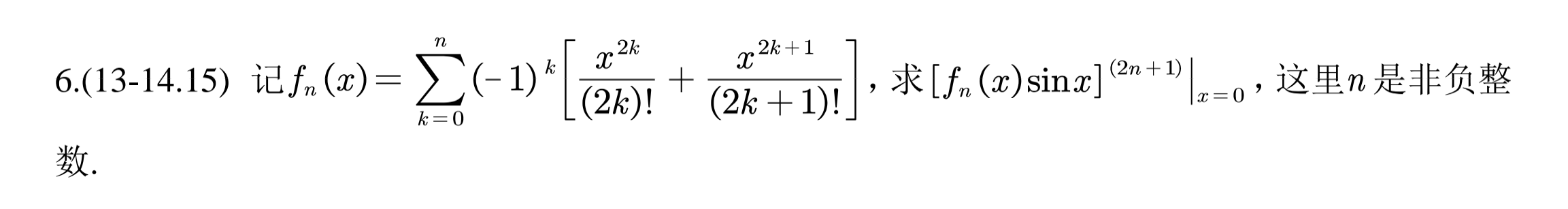
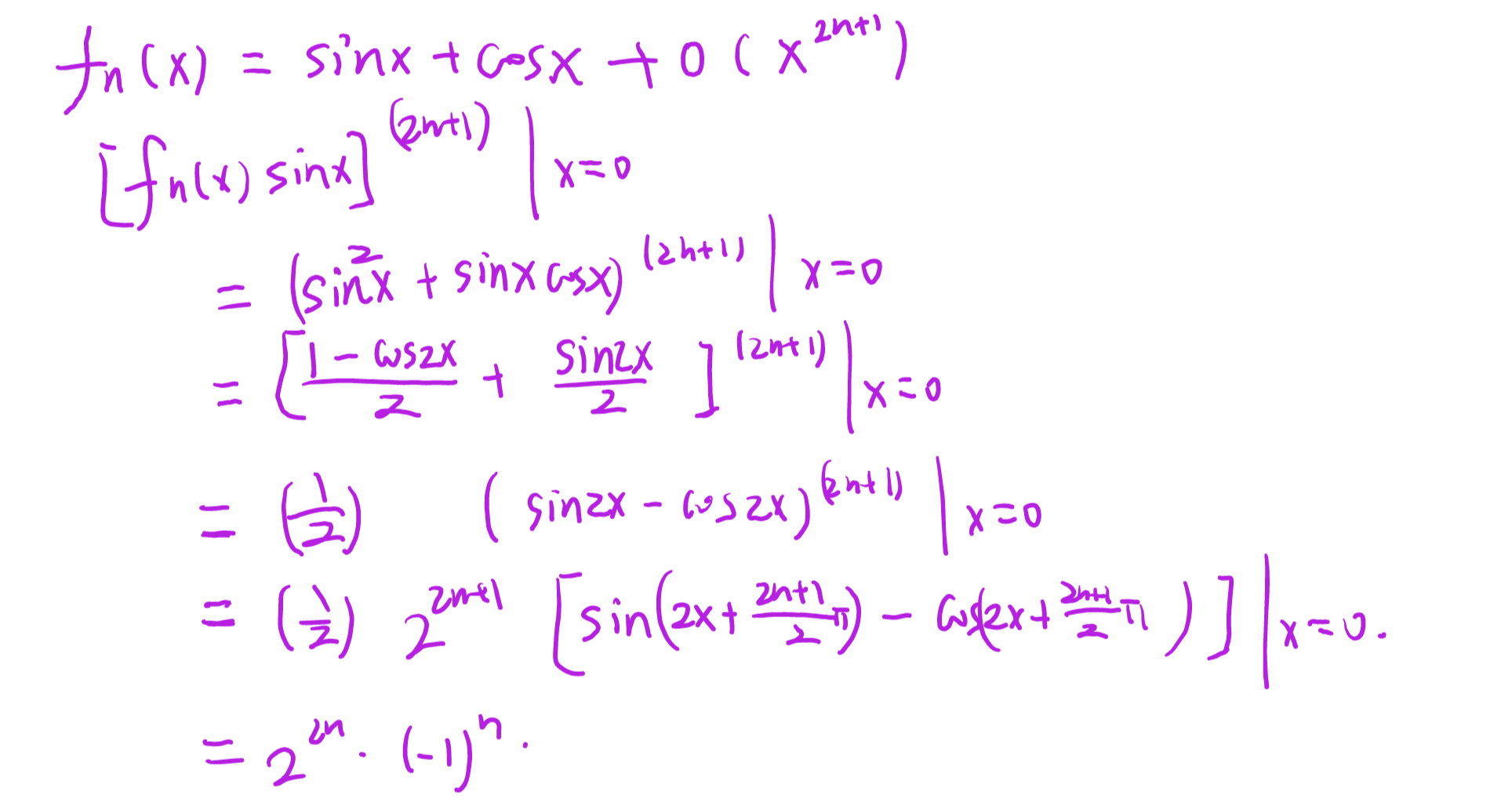
f(x)=(x+a)2ln(x+a),求 f(n)(a)。
还是令 t=x−1,将 ln(x+a) 转化为 ln2a+ln(1+2at) 即可。
-
另外一种间接展开法,就是暴力将某个函数展开为一个多项式加上一个 xn+1 阶余项的做法,比如展开 1/(1−x) 和多项式。基础也是泰勒展开式的唯一性。
-
利用递推关系求高阶导。先将原函数化为函数方程的形式,最好化为多项式函数之类的,如:f(x)=arctanx⇒f′(x)(1+x2)=1,然后用莱布尼兹公式,得到 f(n)(x),f(n−1)(x),⋯ 的关系。
反函数的高阶导数
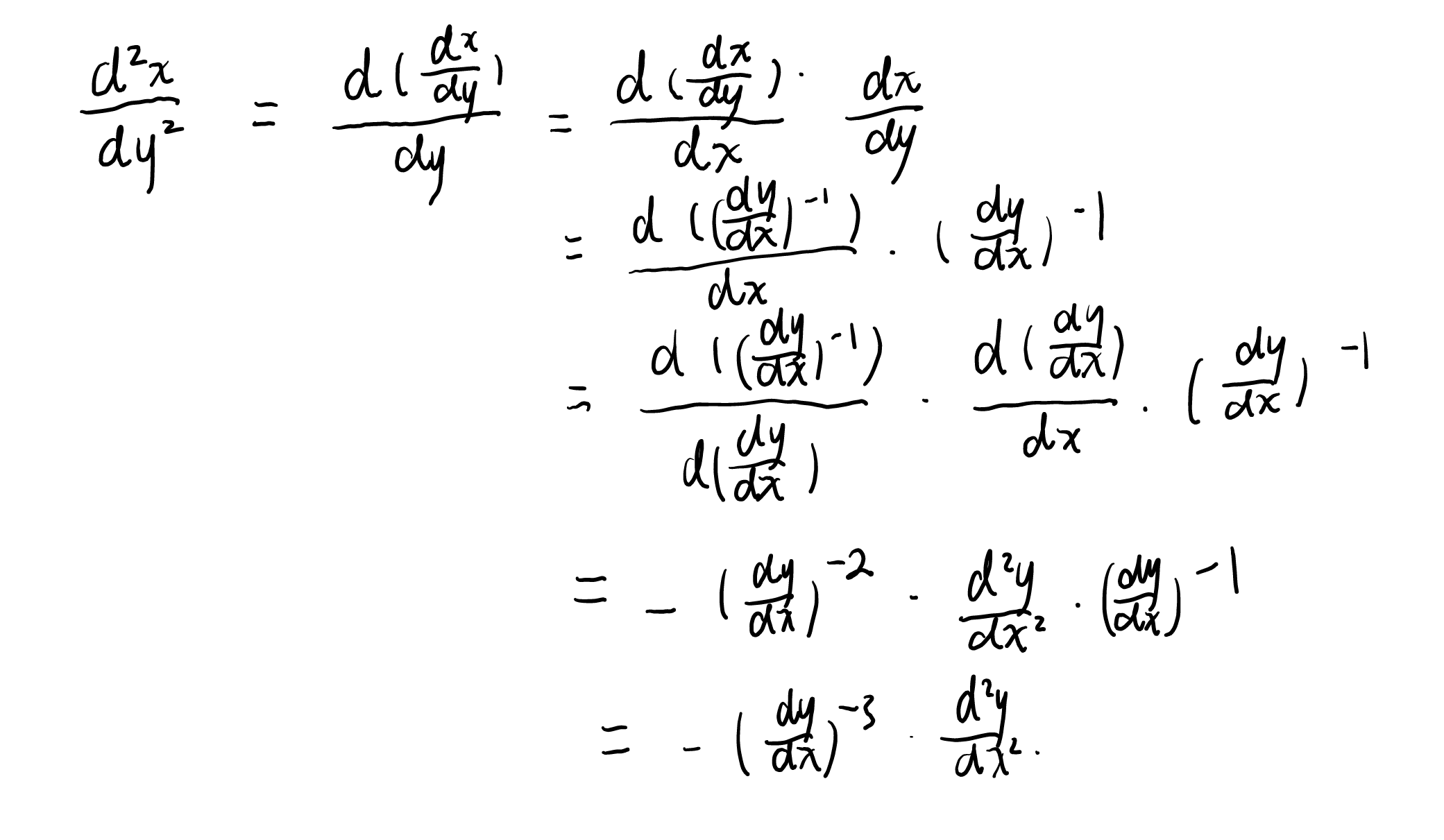
核心是链式求导。
求高阶导数的简便方法还有对数求导法,求导时建议把 y 改写为 y(x) 防止出错。