将矩阵分解为一下正交阵 Q Q Q R R R
且当 R R R
可以使用 Schmidt 正交化,根据 Schmidt 正交化过程,
α i = β i + ∑ j = 1 i − 1 ( β j , α i ) ( β j , β j ) β j \alpha_i=\beta_i+\sum_{j=1}^{i-1} \frac{(\beta_{j},\alpha_i)}{(\beta_j,\beta_j)} \beta_j
α i = β i + j = 1 ∑ i − 1 ( β j , β j ) ( β j , α i ) β j
于是可以根据 β \beta β Q Q Q R R R
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 template <class Num >std::pair<Matrix<Num>,Matrix<Num> > QR (Matrix<Num>A){ assert (A.row==A.col); Matrix<Num>R (A.row,A.col); auto alpha=breakAsVector (A,'C' ); int s=alpha.size (); std::vector<Matrix<Num> >beta; for (int i=1 ;i<=s;++i){ Matrix<Num> beta_i=alpha[i-1 ]; for (int j=1 ;j<=i-1 ;++j){ Num lambda=(alpha[i-1 ]&beta[j-1 ])/(beta[j-1 ]&beta[j-1 ]); beta_i=beta_i-lambda*beta[j-1 ]; R[j][i]=lambda; } R[i][i]=1 ; beta_i.Message="\\beta_" +std::to_string (i); beta.push_back (beta_i); } for (int i=1 ;i<=s;++i){ Num l=length (beta[i-1 ]); beta[i-1 ]=(Num (1 )/Num (l))*beta[i-1 ]; R.times ('R' ,i,l); } Matrix<Num>Q=addH (beta); return std::make_pair (Q.message ("Q" ),R.message ("R" )); }
H = E − 2 ω ω T H=E-2\omega\omega^T
H = E − 2 ω ω T
其中 ∣ ∣ ω ∣ ∣ = 1 ||\omega||=1 ∣ ∣ ω ∣ ∣ = 1
H x Hx H x x x x ω \omega ω
H H H Q Q Q Q Q Q H H H
问题:对 x = ( x 1 , ⋯ , x n ) T ≠ 0 x=(x_1,\cdots,x_n)^T \not=0 x = ( x 1 , ⋯ , x n ) T = 0 ω \omega ω k k k H x = k e 1 Hx=ke_1 H x = k e 1 e 1 = ( 1 , 0 , ⋯ , 0 ) T e_1=(1,0,\cdots,0)^T e 1 = ( 1 , 0 , ⋯ , 0 ) T
先确定常数 k k k H H H k = − s i g n ( x 1 ) ∣ ∣ x ∣ ∣ 2 k=-sign(x_1) ||x||_2 k = − s i g n ( x 1 ) ∣ ∣ x ∣ ∣ 2
这里取 − s i g n ( x 1 ) -sign(x_1) − s i g n ( x 1 ) H H H
令 u = x − k e 1 u=x-ke_1 u = x − k e 1 ω = u ∣ ∣ u ∣ ∣ \omega=\frac{u}{||u||} ω = ∣ ∣ u ∣ ∣ u
证明:几何方法可以证明
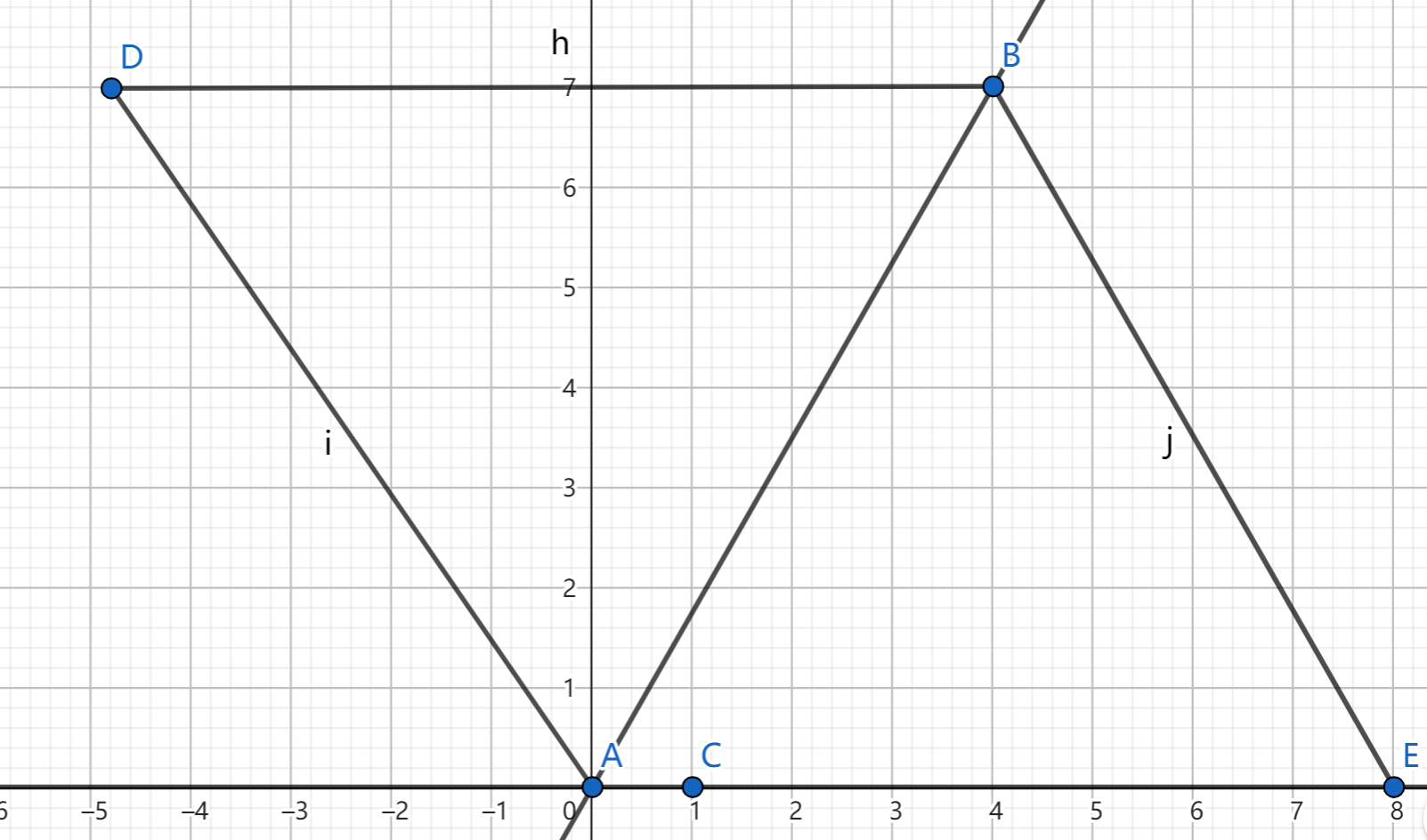
如图,研究 x , e 1 x,e_1 x , e 1 A B AB A B x x x A C AC A C e 1 e_1 e 1 D D D A B D ABD A B D A D = A B − A C × ∣ A B ∣ AD=AB-AC\times |AB| A D = A B − A C × ∣ A B ∣ B E / / A D BE // AD B E / / A D B E BE B E
注意到,可以进一步简化 H H H
H = E − 2 ω ω T = E − β u u T H=E-2\omega\omega^T=E-\beta uu^T
H = E − 2 ω ω T = E − β u u T
β = 2 ( ∣ ∣ u ∣ ∣ 2 ) − 1 = 2 ( ∣ ∣ x − k e 1 ∣ ∣ 2 ) − 1 = 2 ( 2 ( ∣ ∣ x ∣ ∣ 2 + s i g n ( x 1 ) x 1 ∣ ∣ x ∣ ∣ ) ) − 1 = ( ∣ ∣ x ∣ ∣ ( ∣ ∣ x ∣ ∣ + ∣ x 1 ∣ ) ) − 1 \beta=2(||u||^2)^{-1}=2(||x-ke_1||^2)^{-1}=2(2(||x||^2+sign(x_1)x_1||x||))^{-1}\\=(||x||(||x||+|x_1|))^{-1}
β = 2 ( ∣ ∣ u ∣ ∣ 2 ) − 1 = 2 ( ∣ ∣ x − k e 1 ∣ ∣ 2 ) − 1 = 2 ( 2 ( ∣ ∣ x ∣ ∣ 2 + s i g n ( x 1 ) x 1 ∣ ∣ x ∣ ∣ ) ) − 1 = ( ∣ ∣ x ∣ ∣ ( ∣ ∣ x ∣ ∣ + ∣ x 1 ∣ ) ) − 1
代码实现:
1 2 3 4 5 6 7 8 Matrix<Num>x=subMatrix (A,1 ,n,1 ,1 ); Num lx=length (x); Num beta=(Num)(1 )/(Num)(lx*lx+lx*myabs (x[1 ][1 ])); Num sign=(Num)(x[1 ][1 ]>=0 ?1 :-1 ); Num k=-sign*lx; x[1 ][1 ]-=k; Matrix<Num>H=Matrix <Num>(n,n,1 )-beta*x*x.transpose (); A=H*A;
有了上述结论,如何通过 HouseHolder 变换将任意矩阵 A A A
将矩阵 A A A ( x , x 1 , ⋯ , x n − 1 ) (x,x_1,\cdots,x_{n-1}) ( x , x 1 , ⋯ , x n − 1 ) x x x k e 1 ke_1 k e 1 A A A A ′ = ( k e 1 , A x 1 , ⋯ , A x n − 1 ) A'=(ke_1,Ax_1,\cdots,Ax_{n-1}) A ′ = ( k e 1 , A x 1 , ⋯ , A x n − 1 )
第一列已经满足上三角的形式,于是问题转化为将 A 2 ∼ n , 2 ∼ n ′ A'_{2\sim n,2\sim n} A 2 ∼ n , 2 ∼ n ′
1 2 3 Matrix<Num>H=Matrix <Num>(n,n,1 )-beta*x*x.transpose (); A=H*A; auto p=QR_HouseHolder (subMatrix (A,2 ,n,2 ,n));
得到了子矩阵的 Q R QR Q R Q ′ , R ′ Q',R' Q ′ , R ′
Q = H T [ 1 O O Q ′ T ] Q=H^T\begin{bmatrix}1&O\\O & Q'^T\end{bmatrix}
Q = H T [ 1 O O Q ′ T ]
R = [ x 1 . . . O R ′ ] R=\begin{bmatrix}x_1 &...\\O&R'\end{bmatrix}
R = [ x 1 O . . . R ′ ]
如下所示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Matrix<Num>_Q(n,n); _Q[1 ][1 ]=1 ; for (int i=1 ;i<=n-1 ;++i){ for (int j=1 ;j<=n-1 ;++j){ _Q[i+1 ][j+1 ]=p.first[i][j]; } } Matrix<Num>R (n,n); for (int i=1 ;i<=n;++i) R[1 ][i]=A[1 ][i];for (int i=1 ;i<=n-1 ;++i){ for (int j=1 ;j<=n-1 ;++j){ R[i+1 ][j+1 ]=p.second[i][j]; } } return std::make_pair (H.transpose ()*_Q.transpose (),R);
和 HouseHolder 变换差不多,这里不再赘述。
根据特征值的定义 A x = λ x Ax=\lambda x A x = λ x x x x x , A x x,Ax x , A x
幂迭代法的假设:
A A A ∣ λ 1 ∣ > ∣ λ 2 ∣ |\lambda_1|>|\lambda_2| ∣ λ 1 ∣ > ∣ λ 2 ∣
反迭代法和之后的带偏移的QR迭代法思路相近。
使得位移 σ σ σ
期望能直接给出一个理想位移是不太现实的,比较现实的方法就是动态调整,使得位移逐渐靠近某个特征值。
Rayleigh 商迭代的 σ \sigma σ
QR 迭代的收敛性证明比较复杂,这里略去。
这里简要证明 A k + 1 A_{k+1} A k + 1 A k A_k A k
A k + 1 = R k Q k + σ k I = Q k T ( A k − σ k I ) Q k + σ k I = Q k T A k Q k A_{k+1}=R_kQ_k+\sigma_kI=Q_k^T(A_k-\sigma_kI)Q_k+\sigma_kI=Q_k^TA_kQ_k
A k + 1 = R k Q k + σ k I = Q k T ( A k − σ k I ) Q k + σ k I = Q k T A k Q k
σ k \sigma_k σ k σ k \sigma_k σ k A n , n A_{n,n} A n , n σ k \sigma_k σ k A n , n A_{n,n} A n , n A n , 1 ∼ n − 1 A_{n,1\sim n-1} A n , 1 ∼ n − 1 0 0 0
这里有递归的代码实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 template <class Num>std::vector<Num> EigenVals (Matrix<Num>A) { assert (A.row==A.col); int n=A.row; if (n==1 ) return std::vector<Num>{A[1 ][1 ]}; Matrix eye=Matrix <Num>(n,n,1 ); while (true ){ Num sigma=A[n][n]; auto p=QR (A-sigma*eye); Matrix Q=p.first,R=p.second; A=R*Q+sigma*eye; bool flag=true ; for (int i=1 ;i<=n-1 ;++i){ if (!equals (A[n][i],(Num)(0 ))){ flag=false ; break ; } } if (flag) break ; } Num eig_val=A[n][n]; std::vector<Num> eig=EigenVals (subMatrix (A,1 ,n-1 ,1 ,n-1 )); eig.push_back (eig_val); return eig; }
可以使用隐式迭代的方法
首先通过相似变化将 A 转化成一个 上 Hessenberg 矩阵
对这个 Hessenberg 矩阵实施 隐式 QR 迭代
等有时间再写。