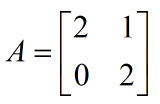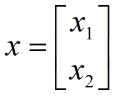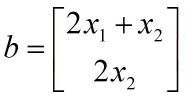主成分分析

矩阵乘法的解释

矩阵乘法可以看做向量的重新组合。

最大可分性

我们有一组 $n$ 维的向量，现在需要降到 $k$ 维（ $k <n$ ），如何选取 $k$ 个基，最大程度地保留原有的信息。

引入：有噪音的一维数据

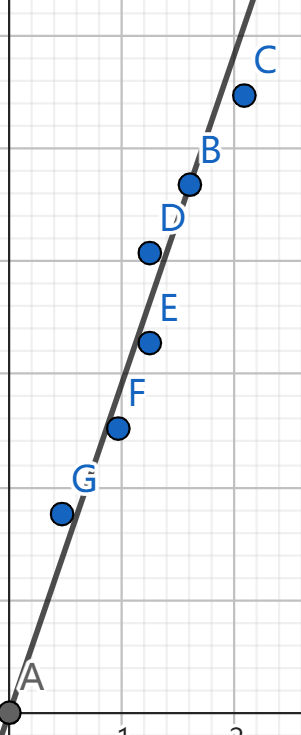
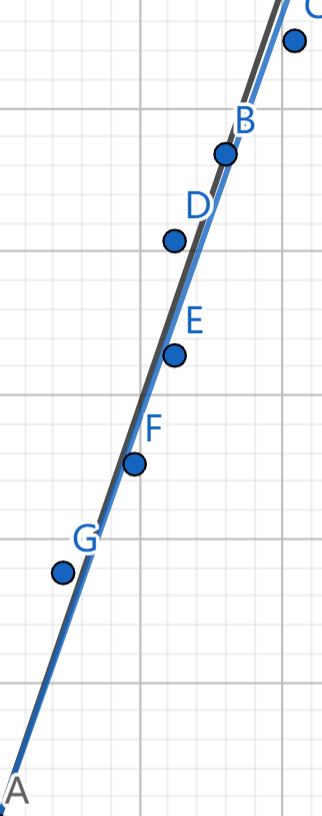
在一条直线附近，我们随便点 $6$ 个点，但是都和原直线有一定的偏差，通过这 $6$ 个点拟合一条直线，我们最先想到的是高中所学的回归法，不过这里我们使用线性代数的方法解决，注意到这 $6$ 个点其实代表了二维的数据，而用一维的直线去拟合，我们想到了 矩阵的对角化。

我们构建：

A=\frac{1}{m} \sum_{i=1}^m v_iv_i^T

可以看出， $A$ 代表了 $v_i$ 的共性。

这里，给出 $6$ 个点的坐标

1.6 4.68
2.08 5.47
1.24 4.07
1.24 3.28
0.96 2.52
0.47 1.76

我们求得 $A$ 矩阵为

1 2	1.85068 5.20433 5.20433 14.7658

可见 $A$ 矩阵非常接近秩一矩阵

接着，进行对角化，得到 $\Lambda$ 为

1 2	16.6019 0 0 0.0145598

于是，抹除第二个特征值，就将原数据拍平到了一维。对角化表示为

Q
0.332707 
0.94303 

Lambda
16.6019 

Q^T
0.332707 0.94303

研究直线 $0.332707 y=0.94303x$ ，可以发现和原直线非常拟合：

成绩预测

我们有一组数据，每列分别代表学生的数学、物理、英语成绩。

我们希望把数据压缩到二维，也就是找到一个平面尽量和原数据拟合。

首先计算 $A$ 矩阵为

1
2
3

6545.78 6537 6362.67 
6537 6545.33 6349.67 
6362.67 6349.67 6278

数据进行对角化，舍去最后一个特征值，得到 $V$ 矩阵

1 2	0.582003 0.581606 0.568337 -0.313846 -0.484097 0.816793

研究两直线 0.582003x=0.581606y=0.568337z 、-0.313846x=-0.484097y=0.816793z 构成的平面，是

1	0.750182x-0.653746y-0.0992112z=0

于是，可以发现数学、物理成绩之间的相关性较高，可以用物理、英语成绩比较准确地预测数学成绩，如：

最后，输入一个未知学生的物理、英语成绩，83 81，得到预测的数学成绩为 83.0425。

成绩预测的优化

我们上面算法的本质是拿一个平面去拟合成绩，但是成绩数值较大，如果成绩在原点附近均匀分布就好了，于是我们想到可以将每一维减去平均值，这称为 中心化：

S=\frac{1}{m-1} \sum_{i=1}^m (v_i-mean)(v_i-mean)^T

这里分母为 $m-1$ 是因为随机变量的数学期望未知，以样本均值替代，自由度减一。

auto cov(std::vector<Matrix<Num> >v){
    v=to_mean(v);
    Matrix<Num>S(v[0].row,v[0].row);
    for (auto x:v) S=S+x*x.transpose();
    return (Num(1)/Num(v[0].row-1))*S;
}

这生成了所谓的协方差矩阵，根据类似的操作，我们得到：

template<class Num>
auto pca(std::vector<Matrix<Num> >v){
    auto S=cov(v);
    int n=S.row;
    auto p=diagonalize(S);
    auto V=p.first.transpose();
    V.resize(n-1,n);
    return baseSolution(V).front();
}

协方差矩阵在运算上的优化

可以发现，将 $v$ 中心化后，组合形成新矩阵 $X$ ，则协方差矩阵

C=\frac{X^TX}{n-1}

而 $X$ 并非方阵，我们采用奇异值分解，推出：

C=\frac{V\Sigma U^TU \Sigma V^T}{n-1}=V\frac{\Sigma^2}{n-1}V^T

这样，可以减少一部分计算量。

template<class Num>
auto pca_with_svd(std::vector<Matrix<Num> >v){
    auto S=addH(to_mean(v));
    int n=S.row;
    Matrix<Num>U,Sigma,V;
    std::tie(U,Sigma,V)=svd(S.transpose());
    V.resize(n-1,n);
    return baseSolution(V).front();
}

二次型极值与 PCA

https://equationliu.github.io/2019-6-25-rmu/