Pólya 定理简明理解

我们以一个经典的例题为例：立方体染色，三种颜色，求本质不同的方案数。

首先我们需要搞清楚什么是“本质不同”，它的意思就是得出的染色方案中，任意两个正方体不能通过旋转操作，使得它们相同。

这就需要我们搞清楚旋转的“表示方法”。

我们通过 置换 来表示一次旋转。有限集合到自身的双射（即一一对应）称为置换。集合 $S=\{a_1,a_2,\cdots,a_n\}$ 上的置换可以表示为：

$f=\binom{a_1,a_2\cdots,a_n}{a_{p1},a_{p2},\cdots,a_{pn}}$

其中 $p_1,p_2,\cdots,p_n$ 是 $1,2,\cdots,n$ 的一个排列。

这里，我们给正方体的面分别编号为 “面1，面2，……，面6”，这里为了方便，简写为 $1,2,\cdots ,6$。

注意这里我们讨论的 $S$ 是面的集合，而不是集合 $\{1,2,\cdots,6\}$。

这里我们考虑一次绕对角线 $120 ^\circ$ 的旋转操作。

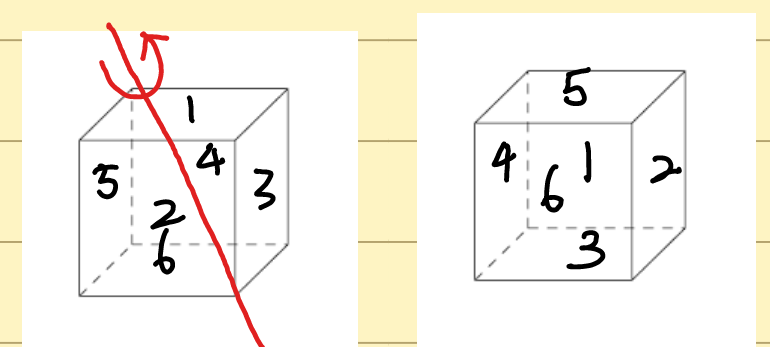
对应的置换就是：

$\binom{1\ 2\ 3\ 4\ 5\ 6}{5\ 6\ 2\ 1\ 4\ 3}$

思考：有多少种染色方法，使得经过这样的置换变换之后，颜色不变？

显然我们需要颜色 $1=5,2=6,3=2,4=1,5=4,6=3$，也就是 $1,5,4$ 颜色相同，$2,3,6$ 颜色相同，一共有 $3^2$ 种染色方法。

思考：如何推广上述的求算方法？

我们将 $1,2,\cdots,n$ 看做节点，将 $(i,p_i)$ 看做一条无向边。处在一个连通块中的节点颜色必须相同。

求证：每个连通块必定是一个环。

每个节点的度数为 $2$，这就说明不会有节点“分支”，也不会出现单独连接一个节点的情况，这说明它就是一个环。

这里我们认为自环也是一个环。

我们引入 循环置换，循环置换是一类特殊的置换，可表示为

$(a_1,a_2,\dots,a_m)=\begin{pmatrix}a_1,a_2,\dots,a_{m-1},a_m\\ a_2,a_3,\dots,a_m,a_1\end{pmatrix}$

再用符号 $\circ$ 来表示置换的组合，那么：

$\binom{1\ 2\ 3\ 4\ 5\ 6}{5\ 6\ 2\ 1\ 4\ 3}=(1,4,5)\circ(2,3,6)$

以此类推，不难证明：

任意一个置换都可以分解为若干不相交的循环置换的乘积。

那么我们就可以说明，设一次旋转对应置换 $g$，令 $c(g)$ 表示置换 $g$ 能够拆分成的不相交的循环置换的数量，这次旋转对应的染色的方法就是 $3^{c(g)}$。

思考：还有没有其他的旋转方法？

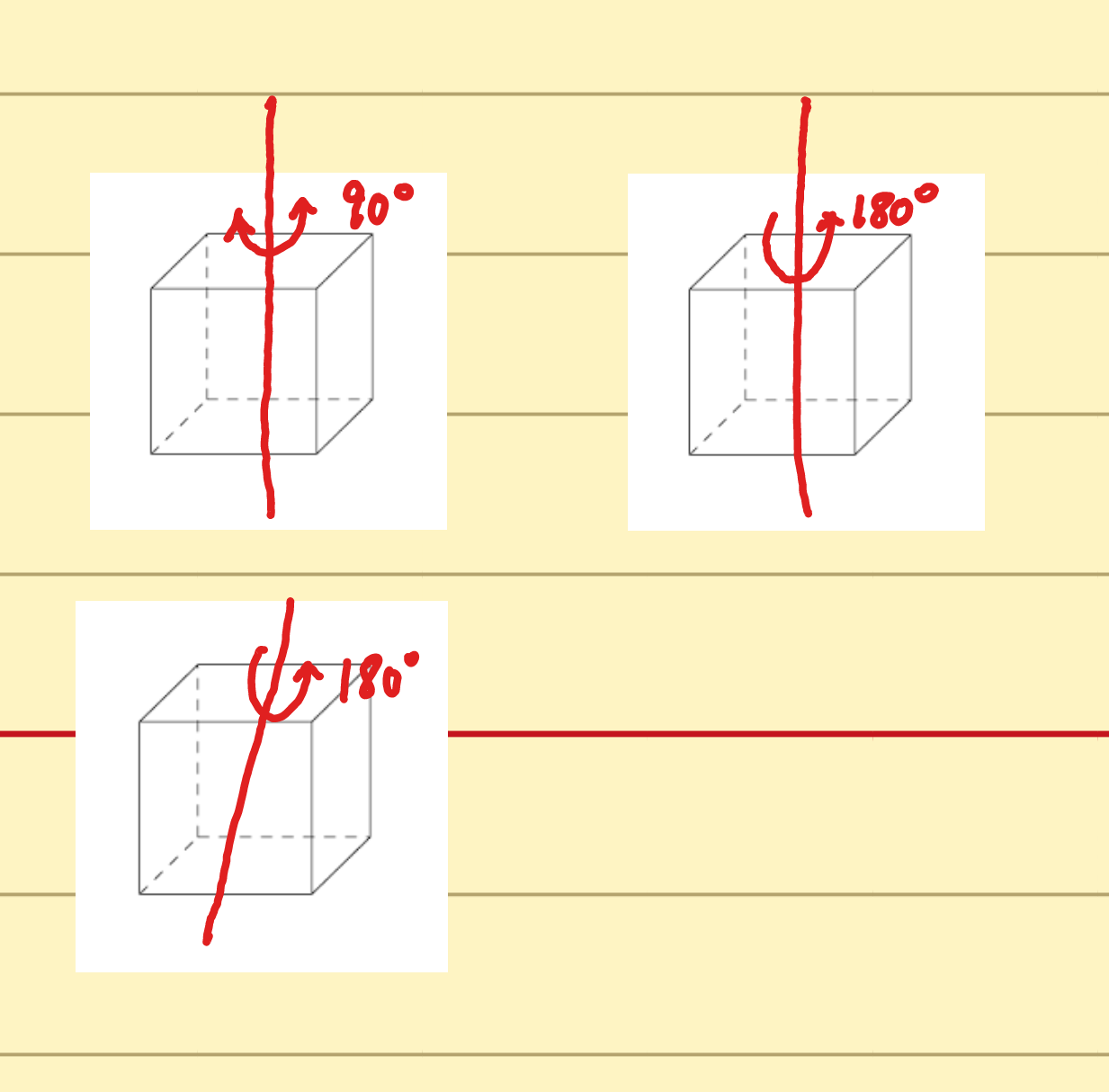
如图，有的，但是如何保证不重不漏我还不清楚。

一共几种旋转方式？

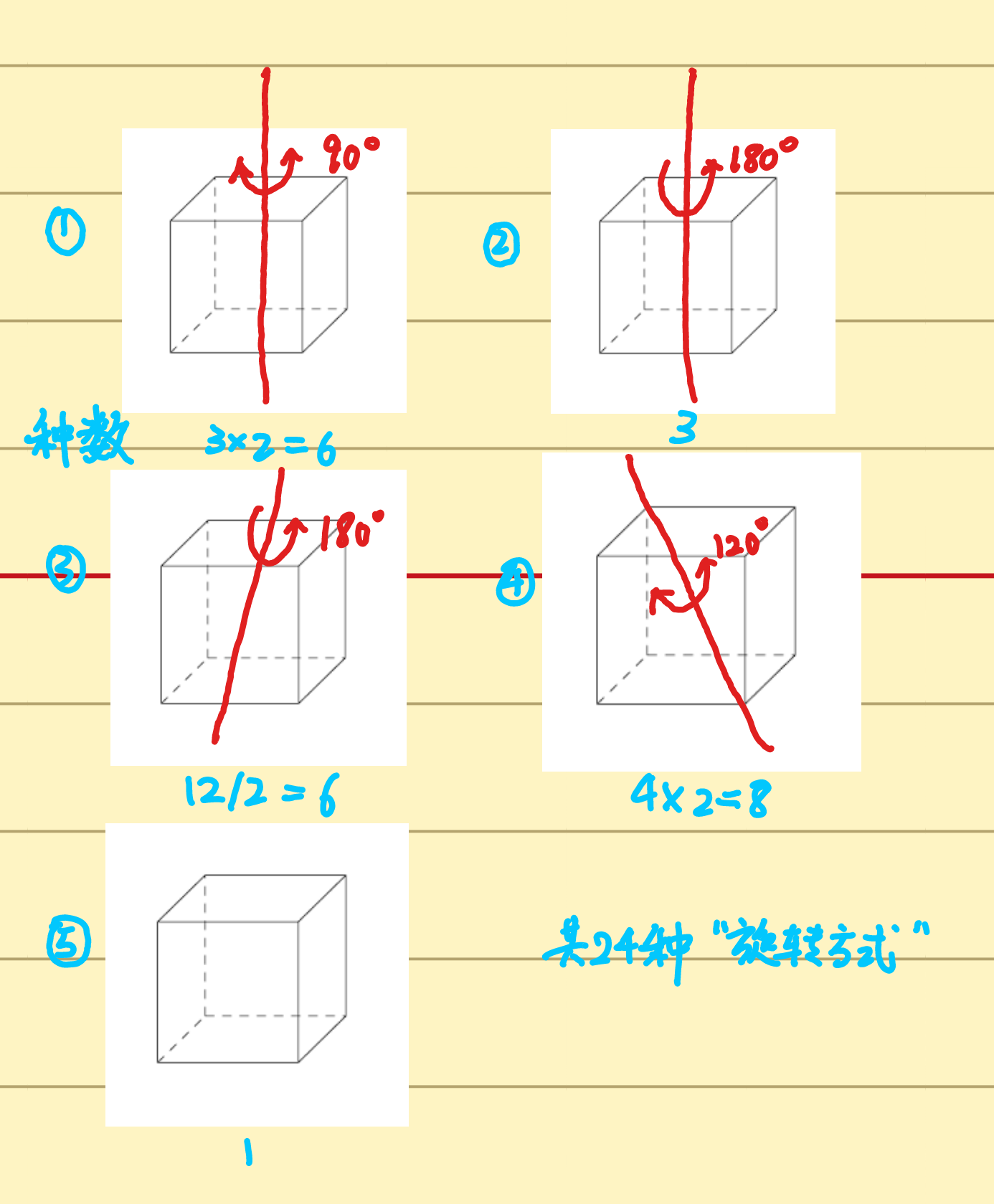
终于到达激动人心的时刻，如何计算本质不同的染色方案。

假设现在我们任意旋转一个染色过的正方体，得到的 $24$ 种结果均不同，那么我们可以高兴地宣布结果是 $3^6/24$，但是显然这不是一个整数。

问题出在了哪里，在于有一些染色的方案旋转之后结果相同，比如说每个面都染成红色，经过任何一种旋转，结果都是相同的。

解决方案也很简单，既然“多除”了，那么就把重复的方案加回去，哪些方案是重复的呢？答案是通过上述 $24$ 种旋转方式结果都相同的染色方案，对于全红来说，在每种旋转方案中，它都是重复的，都要加回去。

计算每种旋转方案重复的染色方案之和。

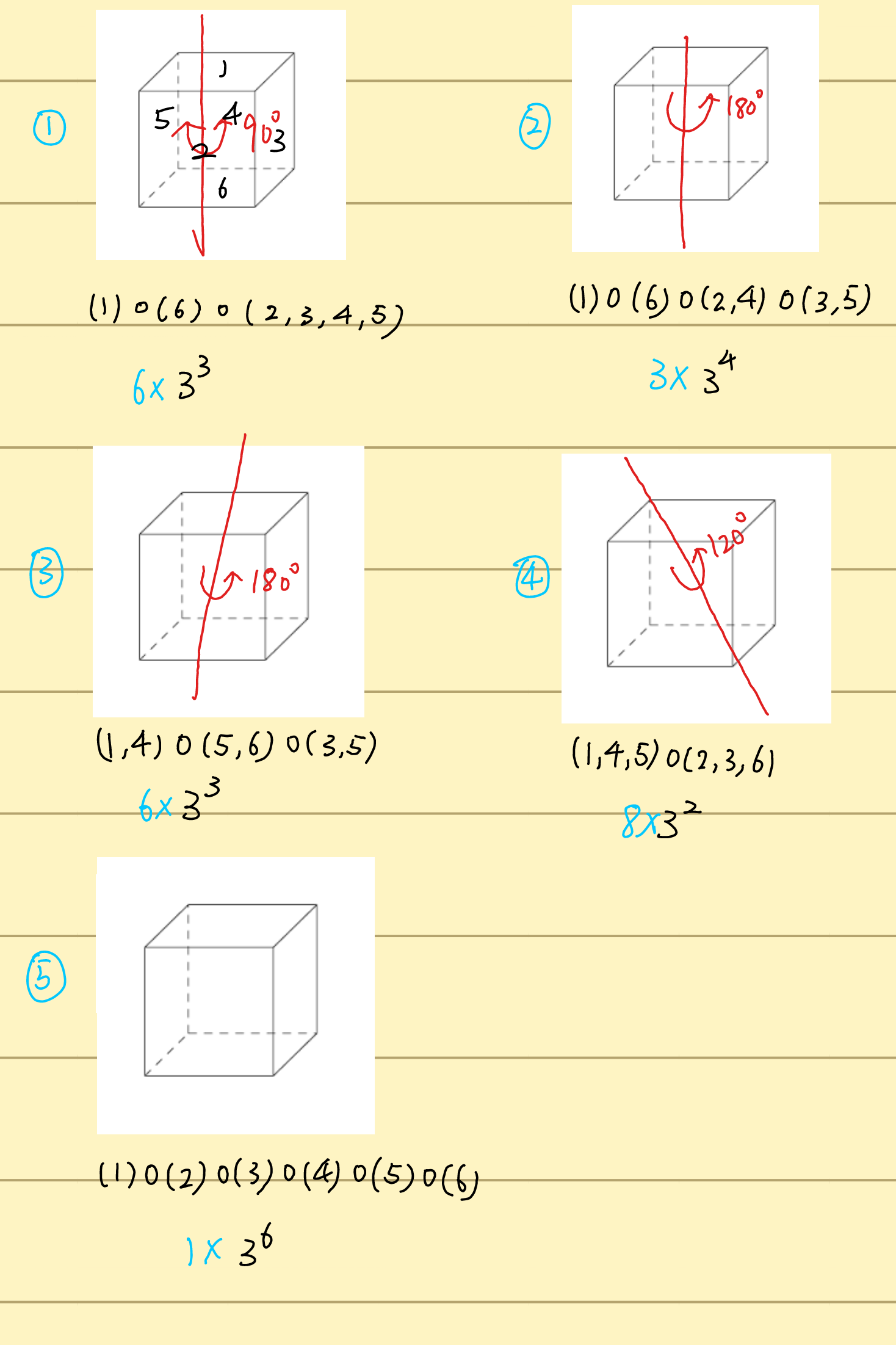
结果是：

$\frac{1}{1+6+3+6+8}(1\times 3^6+6\times3^3+3\times3^4+6\times3^3+8\times3^2)=57$

Pólya 定理的严谨表述

设 $A$ 和 $B$ 为有限集合，$X$ 为所有从 $A$ 到 $B$ 的映射组成的集合。

注：$A$ 为染色载体的集合，如正方体的六个面，$B$ 为颜色的集合。$X$ 就代表一种染色。

$G$ 是 $A$ 上的置换群，且 $X$ 中的映射在 $G$ 中的置换作用下封闭。

注：$G$ 代表旋转的方案。

$X/G$ 表示 $G$ 作用在 $X$ 上产生的所有等价类的集合。
（若 $X$ 中的两个映射经过 $G$ 中的置换作用后相等，则它们在同一等价类中），则

$|X/G|=\frac{1}{|G|}\sum_{g\in G}|B|^{c(g)}$

Pólya 定理之环染色

给定一个 $n$ 个点，$n$ 条边的环，有 $n$ 种颜色，给每个顶点染色，问有多少种本质不同的染色方案，答案对 $10^9+7$ 取模。

注意本题的本质不同，定义为：只需要不能通过旋转与别的染色方案相同。

$G$ 为旋转 $0,1,\cdots,n-1$ 格，旋转 $k$ 格时，我们发现 $c(g)=\gcd(n,k)$。

注：考虑辗转相减法，$pk\equiv m \pmod n$ 得到的最小 $m$ 就是 $\gcd(n,k)$，也就是相差 $\gcd(n,k)$ 的整数倍的点才可以通过旋转关联，共 $\gcd(n,k)$ 个连通块。

答案是 $\frac{1}{n} \sum_{k=1}^n n^{\gcd(n,k)}$。