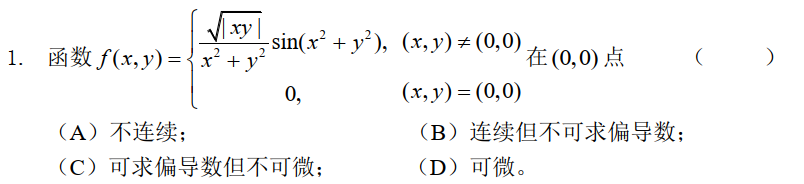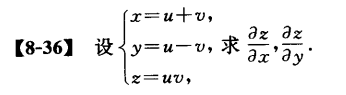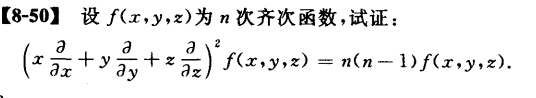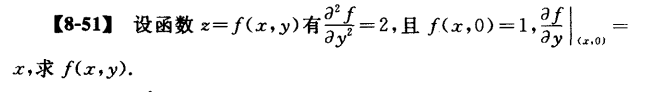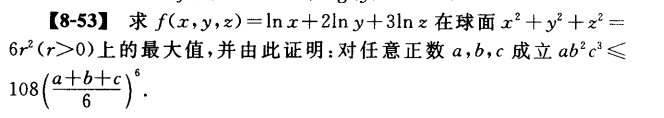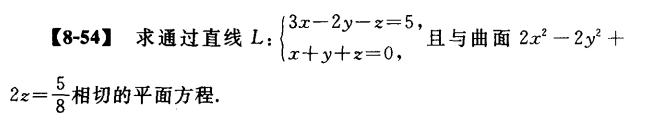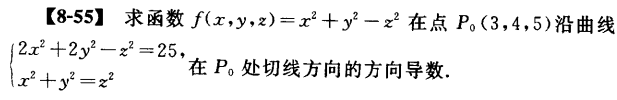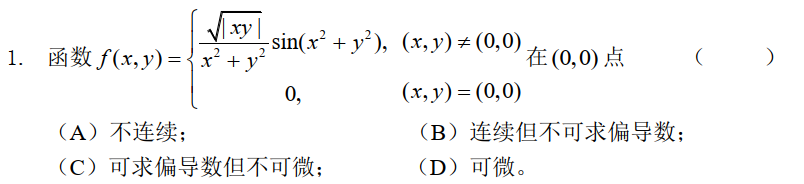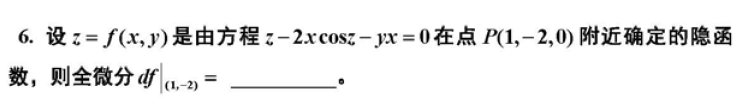点之间的距离小于 δ \delta δ
内点/外点/边界点
若点 M ∈ E M\in E M ∈ E U ( M ) U(M) U ( M ) E E E U ( M ) ⊂ E U(M) \sub E U ( M ) ⊂ E
若点 M ∉ E M\notin E M ∈ / E U ( M ) U(M) U ( M ) E E E
对于任意一个邻域 U ( M ) U(M) U ( M ) M M M E E E
开集与闭集/区域/有界性
点集 E E E
连通的开集称为开区域,简称区域,常用 D D D
如何很好地定义连通是个问题,现在的定义是用折线连接,但是感觉不太好证明连通,一个曲线是不是连通的呢?
设 E E E O O O ∃ r > 0 \exists r >0 ∃ r > 0 E ⊂ U ( O , r ) E \sub U(O,r) E ⊂ U ( O , r ) E E E E E E
这个定义有点类似于无界数集的定义,关键在于理解邻域。
n n n
f ( x , y ) f(x,y) f ( x , y ) D D D M 0 ( x 0 , y 0 ) M_0(x_0,y_0) M 0 ( x 0 , y 0 ) D D D lim x → 0 sin x / x = 1 \lim_{x\to0} \sin x/x=1 lim x → 0 sin x / x = 1 A A A ε \varepsilon ε δ \delta δ
0 < ρ = ∣ M M 0 ∣ = ( x − x 0 ) 2 + ( y − y 0 ) 2 < δ ( 注 : 邻 域 U ( ( x 0 , y 0 ) , δ ) ) 0<\rho=|MM_0|=\sqrt{(x-x_0)^2+(y-y_0)^2}<\delta(注:邻域 U((x_0,y_0),\delta))
0 < ρ = ∣ M M 0 ∣ = ( x − x 0 ) 2 + ( y − y 0 ) 2 < δ ( 注 : 邻 域 U ( ( x 0 , y 0 ) , δ ) )
的点 M ( x , y ) ∈ D M(x,y)\in D M ( x , y ) ∈ D ∣ f ( x , y ) − A ∣ < ε |f(x,y)-A|<\varepsilon ∣ f ( x , y ) − A ∣ < ε
则称常数 A A A f ( x , y ) f(x,y) f ( x , y ) ( x , y ) → ( x 0 , y 0 ) (x,y)\to(x_0,y_0) ( x , y ) → ( x 0 , y 0 )
表示方法
lim ( x , y ) → ( x 0 , y 0 ) f ( x , y ) = A \lim_{(x,y)\to(x_0,y_0)} f(x,y)=A
( x , y ) → ( x 0 , y 0 ) lim f ( x , y ) = A
或
lim x → x 0 y → y 0 f ( x , y ) = A \lim_{x\to x_0 \, y\to y_0} f(x,y)=A
x → x 0 y → y 0 lim f ( x , y ) = A
二重极限不等于二次极限 。例如经典反例 z = 0 , x = 0 ; y , x ≠ 0 z=0,x=0;y,x\not=0 z = 0 , x = 0 ; y , x = 0 lim y → 0 lim x → 0 z = 0 \lim_{y\to 0}\lim_{x\to 0} z=0 lim y → 0 lim x → 0 z = 0 lim ( x , y ) → ( 0 , 0 ) z \lim_{(x,y) \to (0,0)} z lim ( x , y ) → ( 0 , 0 ) z
二重极限要求从二维的方向逼近。
极限的唯一性、有界性、保号性
结论:设函数 f ( x , y ) f(x,y) f ( x , y ) R 2 \R^2 R 2 x , y x,y x , y f ( x , y ) f(x,y) f ( x , y ) R 2 \R^2 R 2
判断
lim ( x , y ) → ( x 0 , y 0 ) x y x + y \lim_{(x,y)\to(x_0,y_0)} \frac{xy}{x+y}
( x , y ) → ( x 0 , y 0 ) lim x + y x y
是否存在。
考虑到 x = 0 , y = δ / 2 x=0,y=\delta/2 x = 0 , y = δ / 2 0 0 0 x ≈ − y x\approx-y x ≈ − y
事实上,函数在任何一个去心邻域中都存在无穷中断点。间断曲线 y = − x y=-x y = − x
判断
lim ( x , y ) → ( 0 , 0 ) x 2 y 2 x − y \lim_{(x,y)\to(0,0)} \frac{x^2y}{2x-y}
( x , y ) → ( 0 , 0 ) lim 2 x − y x 2 y
思路是使 2 x − y 2x-y 2 x − y x 2 y x^2y x 2 y
\lim _{\substack{(x, y) \rightarrow(0,0) \\ y=2 x+k x^3}} \frac{x^2 y}{2 x-y}=\lim _{x \rightarrow 0} \frac{x^2\left(2 x+k x^3\right)}{k x^3}=\frac{2}{k},
极限值不唯一, 故极限不存在。\lim _{\substack{(x, y) \rightarrow(0,0) \\ y=2 x+x^4}} \frac{x^2 y}{2 x-y}=\lim _{x \rightarrow 0} \frac{x^2\left(2 x+x^4\right)}{x^4}=\infty , 故极限不存在。
\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{x^2 y^4+x^3 y^3+x^4 y^2}{x^4+y^4} \sin \left(\frac{1}{x^4+y^4}\right)
夹逼定理结合定义。可以凑出关于 x 2 + y 2 x^2+y^2 x 2 + y 2
原 式 ≤ x 2 y 2 ∣ x 2 + x y + y 2 ∣ x 4 + y 4 ⋅ 1 ≤ 1 2 ∣ x 2 + x y + y 2 ∣ ≤ 1 2 [ ∣ x y ∣ + ( x 2 + y 2 ) ] ⋯ 原式 \le \frac{x^2y^2|x^2+xy+y^2|}{x^4+y^4} \cdot 1\le \frac{1}{2} |x^2+xy+y^2| \le \frac{1}{2} [|xy|+(x^2+y^2)] \cdots
原 式 ≤ x 4 + y 4 x 2 y 2 ∣ x 2 + x y + y 2 ∣ ⋅ 1 ≤ 2 1 ∣ x 2 + x y + y 2 ∣ ≤ 2 1 [ ∣ x y ∣ + ( x 2 + y 2 ) ] ⋯
多元函数的极限同样满足加法、乘法、除法定律。
二元函数的连续性。
连续的定义:
若:
lim x → x 0 y → y 0 f ( x , y ) = f ( x 0 , y 0 ) \lim_{x\to x_0 \, y\to y_0} f(x,y)=f(x_0,y_0)
x → x 0 y → y 0 lim f ( x , y ) = f ( x 0 , y 0 )
则称 z = f ( x , y ) z=f(x,y) z = f ( x , y ) M 0 ( x 0 , y 0 ) M_0(x_0,y_0) M 0 ( x 0 , y 0 )
A. 设 f ( x , y ) = ∣ x ∣ + ∣ y ∣ f(x,y)=|x|+|y| f ( x , y ) = ∣ x ∣ + ∣ y ∣
B. 可以说明
C,D. 构造分段函数即可。或取 f ( x , y ) = 1 f(x,y)=1 f ( x , y ) = 1
用极坐标换元来估计极限
lim ( x , y ) → ( 0 , 0 ) f ( x , y ) = A ∀ ε > 0 , ∃ δ > 0 , 0 < r = x 2 + y 2 < δ ∣ f ( x , y ) − A ∣ < ε \lim_{(x,y)\to(0,0)}f(x,y)=A \quad \forall \varepsilon >0,\exists \delta>0,0<r=\sqrt{x^2+y^2}<\delta\\
|f(x,y)-A|<\varepsilon
( x , y ) → ( 0 , 0 ) lim f ( x , y ) = A ∀ ε > 0 , ∃ δ > 0 , 0 < r = x 2 + y 2 < δ ∣ f ( x , y ) − A ∣ < ε
极坐标下改写
lim r → 0 + f ( x , y ) = A ∀ ε > 0 , ∃ δ > 0 , 0 < r = x 2 + y 2 < δ ∣ f ( r cos θ , r sin θ ) − A ∣ < ε \lim_{r \to 0^+}f(x,y)=A \quad \forall \varepsilon >0,\exists \delta>0,0<r=\sqrt{x^2+y^2}<\delta\\
|f(r\cos\theta,r\sin\theta)-A|<\varepsilon
r → 0 + lim f ( x , y ) = A ∀ ε > 0 , ∃ δ > 0 , 0 < r = x 2 + y 2 < δ ∣ f ( r cos θ , r sin θ ) − A ∣ < ε
如果 θ = θ ( r ) \theta=\theta(r) θ = θ ( r ) r → 0 + r \to 0^+ r → 0 +
极坐标换元的好处是,当 ( x , y ) → ( 0 , 0 ) (x,y) \to (0,0) ( x , y ) → ( 0 , 0 ) r → 0 r \to 0 r → 0 θ \theta θ
比如说分析
lim ( x , y ) → ( 0 , 0 ) x 3 y + x 2 y 2 + x y 3 x + y \lim_{(x,y) \to (0,0)}\frac{x^3y+x^2y^2+xy^3}{x+y}
( x , y ) → ( 0 , 0 ) lim x + y x 3 y + x 2 y 2 + x y 3
就可以得到
r 3 ( cos 3 θ sin θ + cos 2 θ sin 2 θ + cos θ sin 3 θ ) cos θ + sin θ \frac{r^3(\cos ^3 \theta\sin\theta+\cos^2\theta\sin^2\theta+\cos \theta\sin^3\theta)}{\cos \theta+\sin\theta}
cos θ + sin θ r 3 ( cos 3 θ sin θ + cos 2 θ sin 2 θ + cos θ sin 3 θ )
因此,可以看出分子是有边界的。但是可以通过控制分母,达到无穷大或者限制在一定范围之内。
总结 二元函数的极限,做法是:
平移到坐标原点,计算 x → 0 , y → 0 x\to0,y\to0 x → 0 , y → 0
极坐标换元。y = k x y=kx y = k x
观察分母和分子的阶数。
使得分母为高阶无穷小,如果它能等于 0 的话。
设二元函数 z = f ( x , y ) z=f(x,y) z = f ( x , y ) M 0 ( x 0 , y 0 ) M_0(x_0,y_0) M 0 ( x 0 , y 0 ) U ( M 0 ) U(M_0) U ( M 0 ) x , y x,y x , y x 0 , y 0 x_0,y_0 x 0 , y 0 Δ x , Δ y \Delta x,\Delta y Δ x , Δ y Δ z \Delta z Δ z
Δ z = f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 ) \Delta z=f(x_0+\Delta x,y_0+\Delta y)-f(x_0,y_0)
Δ z = f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 )
记偏增量:
Δ x z = f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) \Delta_x z=f(x_0+\Delta x,y_0)-f(x_0,y_0)
Δ x z = f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 )
偏导数:
若
极限:
lim Δ x → 0 Δ x z Δ x = lim Δ x → 0 f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) Δ x \lim_{\Delta x\to0} \frac{\Delta_x z}{\Delta x}=\lim_{\Delta x\to 0}\frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x}
Δ x → 0 lim Δ x Δ x z = Δ x → 0 lim Δ x f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 )
存在,则即偏导数 ∂ z ∂ x ∣ ( x 0 , y 0 ) \displaystyle \frac{\partial z}{\partial x}|_{(x_0,y_0)} ∂ x ∂ z ∣ ( x 0 , y 0 )
偏导数的几何意义:取平面曲线 z = f ( x , y 0 ) z=f(x,y_0) z = f ( x , y 0 )

偏导数的定义
∂ z ∂ x ∣ ( x 0 , y 0 ) = z x = f x ( x , y ) = lim Δ x → 0 f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) Δ x \left.\frac{\partial z}{\partial x}\right|_{(x_0,y_0)}=z_x=f_x(x,y)=\lim_{\Delta x\to 0}\frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x}
∂ x ∂ z ∣ ∣ ∣ ∣ ( x 0 , y 0 ) = z x = f x ( x , y ) = Δ x → 0 lim Δ x f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 )
当 两个二阶混合偏导数在 D D D 时,有:
\frac{\partial ^2z}{\partial x\partial y}=\frac{\partial^2 z}{\part y\part x}
证明:
令 φ = f ( x + Δ x , y + Δ y ) − f ( x , y + Δ y ) − f ( x + Δ x , y ) + f ( x , y ) \varphi=f(x+\Delta x,y+\Delta y)-f(x,y+\Delta y)-f(x+\Delta x,y)+f(x,y) φ = f ( x + Δ x , y + Δ y ) − f ( x , y + Δ y ) − f ( x + Δ x , y ) + f ( x , y )
令向后差分算子
Δ y f ( x , y ) = f ( x , y + Δ y ) − f ( x , y ) = L a g r a n g e f 2 ( x , η ) Δ y ( 连 续 ) Δ x f ( x , y ) = f ( x + Δ x , y ) − f ( x , y ) = L a g r a n g e f 1 ( ξ , y ) Δ x \Delta_y f(x,y)=f(x,y+\Delta y)-f(x,y)\overset{\mathrm{Lagrange}}= f_2(x,\eta) \Delta y (连续)\\
\Delta_x f(x,y)=f(x+\Delta x,y)-f(x,y)\overset{\mathrm{Lagrange}}= f_1(\xi,y)\Delta x
Δ y f ( x , y ) = f ( x , y + Δ y ) − f ( x , y ) = L a g r a n g e f 2 ( x , η ) Δ y ( 连 续 ) Δ x f ( x , y ) = f ( x + Δ x , y ) − f ( x , y ) = L a g r a n g e f 1 ( ξ , y ) Δ x
φ = Δ x Δ y f = Δ y Δ x f = Δ x Δ y f 12 ( ξ , η ) = Δ y Δ x f 21 ( α , β ) \varphi=\Delta_x\Delta_y f=\Delta_y \Delta_x f=\Delta x\Delta yf_{12}(\xi,\eta)=\Delta y \Delta x f_{21} (\alpha,\beta)
φ = Δ x Δ y f = Δ y Δ x f = Δ x Δ y f 1 2 ( ξ , η ) = Δ y Δ x f 2 1 ( α , β )
取极限的时候,即 Δ x → 0 , Δ y → 0 \Delta x \to0,\Delta y \to0 Δ x → 0 , Δ y → 0
( ξ , η ) , ( α , β ) → ( x , y ) (\xi,\eta),(\alpha,\beta) \to(x,y)
( ξ , η ) , ( α , β ) → ( x , y )
因此,f 12 ( x , y ) , f 21 ( x , y ) f_{12}(x,y),f_{21}(x,y) f 1 2 ( x , y ) , f 2 1 ( x , y )
Laplace 算子:
Δ = ∂ 2 ∂ x 2 + ∂ 2 ∂ y 2 + ∂ 2 ∂ z 2 \Delta =\frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial y^2}+\frac{\partial ^2}{\partial z^2}
Δ = ∂ x 2 ∂ 2 + ∂ y 2 ∂ 2 + ∂ z 2 ∂ 2
Laplace 方程:
Δ u = 0 \Delta u=0
Δ u = 0
计算偏导数时,和计算一元函数导数一样,也要关注分段函数的分段点和无定义点的问题。
计算高阶偏导数,例如 f x y ( x 0 , y 0 ) f_{xy}(x_0,y_0) f x y ( x 0 , y 0 ) f x ( x 0 , y ) f_x(x_0,y) f x ( x 0 , y ) y y y
注意偏导数是多元函数。
设 u = f ( x , y , z ) u=f(x, y, z) u = f ( x , y , z ) f x x = f y y = f z z \frac{f_x}{x}=\frac{f_y}{y}=\frac{f_z}{z} x f x = y f y = z f z u u u r r r r = x 2 + y 2 + z 2 r=\sqrt{x^2+y^2+z^2} r = x 2 + y 2 + z 2 u = f ( x , y , z ) = u ( r ) u=f(x, y, z)=u(r) u = f ( x , y , z ) = u ( r ) ⇔ \Leftrightarrow ⇔ S r : x 2 + y 2 + z 2 = r 2 S_r: x^2+y^2+z^2=r^2 S r : x 2 + y 2 + z 2 = r 2 u = f ( x , y , z ) u=f(x, y, z) u = f ( x , y , z ) ⇔ \Leftrightarrow ⇔ x 2 + y 2 + z 2 = r \sqrt{x^2+y^2+z^2}=r x 2 + y 2 + z 2 = r f ( x , y , z ) f(x, y, z) f ( x , y , z ) 1 f ( x , y , z ) 1 f(x, y, z) 1 f ( x , y , z ) F ( x , y , z ) = f ( x , y , z ) − c = 0 F(x, y, z)=f(x, y, z)-c=0 F ( x , y , z ) = f ( x , y , z ) − c = 0 ∇ F ( x , y , z ) = ∇ f ( x , y , z ) = ( f x , f y , f z ) \nabla F(x, y, z)=\nabla f(x, y, z)=\left(f_x, f_y, f_z\right) ∇ F ( x , y , z ) = ∇ f ( x , y , z ) = ( f x , f y , f z ) S r : g ( x , y , z ) = x 2 + y 2 + z 2 − r 2 = 0 S_r: g(x, y, z)=x^2+y^2+z^2-r^2=0 S r : g ( x , y , z ) = x 2 + y 2 + z 2 − r 2 = 0 ∇ g = ( 2 x , 2 y , 2 z ) \nabla g=(2 x, 2 y, 2 z) ∇ g = ( 2 x , 2 y , 2 z ) f x x = f y y = f z z \frac{f_x}{x}=\frac{f_y}{y}=\frac{f_z}{z} x f x = y f y = z f z ⇒ S r : g ( x , y , z ) = x 2 + y 2 + z 2 − r 2 = 0 \Rightarrow S_r: g(x, y, z)=x^2+y^2+z^2-r^2=0 ⇒ S r : g ( x , y , z ) = x 2 + y 2 + z 2 − r 2 = 0 f f f u = f ( x , y , z ) = u ( r ) u=f(x, y, z)=u(r) u = f ( x , y , z ) = u ( r )
已知 f ( x , y ) = ( x y + x y 2 ) e x + y f(x, y)=\left(x y+x y^2\right) e^{x+y} f ( x , y ) = ( x y + x y 2 ) e x + y ∂ 10 f ∂ x 5 ∂ y 5 = \frac{\partial^{10} f}{\partial x^5 \partial y^5}= ∂ x 5 ∂ y 5 ∂ 1 0 f = ∂ 10 f ∂ x 5 ∂ y 5 = ( x e x ) ( 5 ) [ ( y + y 2 ) e y ] ( 5 ) \frac{\partial^{10} f}{\partial x^5 \partial y^5}=\left(x e^x\right)^{(5)}\left[\left(y+y^2\right) e^y\right]^{(5)} ∂ x 5 ∂ y 5 ∂ 1 0 f = ( x e x ) ( 5 ) [ ( y + y 2 ) e y ] ( 5 )
= ( x e x + 5 e x ) [ ( y + y 2 ) + 5 ( 1 + 2 y ) + C 5 2 2 ] e y = ( x + 5 ) ( y 2 + 11 y + 25 ) e x + y = ( x y 2 + 11 x y + 25 x + 5 y 2 + 55 y + 125 ) e x + y \begin{aligned}
& =\left(x e^x+5 e^x\right)\left[\left(y+y^2\right)+5(1+2 y)+C_5^2 2\right] e^y \\
& =(x+5)\left(y^2+11 y+25\right) e^{x+y} \\
& =\left(x y^2+11 x y+25 x+5 y^2+55 y+125\right) e^{x+y}
\end{aligned}
= ( x e x + 5 e x ) [ ( y + y 2 ) + 5 ( 1 + 2 y ) + C 5 2 2 ] e y = ( x + 5 ) ( y 2 + 1 1 y + 2 5 ) e x + y = ( x y 2 + 1 1 x y + 2 5 x + 5 y 2 + 5 5 y + 1 2 5 ) e x + y
已知 z = x ln ( ( 1 + y 2 ) e x 2 sin y ) z=x\ln((1+y^2)e^{x^2 \sin y}) z = x ln ( ( 1 + y 2 ) e x 2 sin y ) ∂ 2 z ∂ y 2 ∂ x 2 = \frac{\partial^2 z}{\partial y^2 \partial x^2}= ∂ y 2 ∂ x 2 ∂ 2 z =
得到 z = x ( ln ( 1 + y 2 ) + x 2 sin y ) z=x(\ln(1+y^2)+x^2\sin y) z = x ( ln ( 1 + y 2 ) + x 2 sin y ) x x x
( x 3 ) ( 2 ) ( sin y ) ( 2 ) (x^3)^{(2)}(\sin y)^{(2)}
( x 3 ) ( 2 ) ( sin y ) ( 2 )
多元函数可微的引入:一元函数微分的定义 :
Δ y = f ( x 0 + Δ x ) − f ( x 0 ) \Delta y=f(x_0+\Delta x)-f(x_0)
Δ y = f ( x 0 + Δ x ) − f ( x 0 )
可表示为 Δ y = A Δ x + o ( Δ x ) \Delta y=A \Delta x+o(\Delta x) Δ y = A Δ x + o ( Δ x ) y = f ( x ) y=f(x) y = f ( x ) x = x 0 x=x_0 x = x 0 d y ∣ x 0 = A Δ x \mathrm d y|_{x_0}=A\Delta x d y ∣ x 0 = A Δ x
对于一元函数,可微和可导等价。
可微的定义 :
如果函数 f ( x , y ) f(x,y) f ( x , y ) ( x 0 , y 0 ) (x_0,y_0) ( x 0 , y 0 ) Δ z = f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 ) \Delta z=f(x_0+\Delta x,y_0+\Delta y)-f(x_0,y_0) Δ z = f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 )
Δ z = A Δ x + B Δ y + o ( ρ ) \Delta z=A\Delta x+B\Delta y+o(\rho)
Δ z = A Δ x + B Δ y + o ( ρ )
其中 ρ = ( Δ x ) 2 + ( Δ y ) 2 \rho=\sqrt{(\Delta x)^2+(\Delta y)^2} ρ = ( Δ x ) 2 + ( Δ y ) 2 f ( x , y ) f(x,y) f ( x , y )
可微判定的条件 :
若 f x ( x 0 , y 0 ) f_x(x_0,y_0) f x ( x 0 , y 0 ) f y ( x 0 , y 0 ) f_y(x_0,y_0) f y ( x 0 , y 0 )
lim ( Δ x , Δ y ) → ( x 0 , y 0 ) Δ z − f x ( x 0 , y 0 ) Δ x − f y ( x 0 , y 0 ) Δ y Δ x 2 + Δ y 2 \lim_{(\Delta x,\Delta y) \to (x_0,y_0)} \frac{\Delta z-f_x(x
_0,y_0)\Delta x-f_y(x_0,y_0)\Delta y}{\sqrt{\Delta x^2 + \Delta y^2}}
( Δ x , Δ y ) → ( x 0 , y 0 ) lim Δ x 2 + Δ y 2 Δ z − f x ( x 0 , y 0 ) Δ x − f y ( x 0 , y 0 ) Δ y
存在且等于 0。可以证明,如果这个极限存在,则必定为0,否则出现矛盾。
则称函数在点 ( x 0 , y 0 ) (x_0,y_0) ( x 0 , y 0 )
当 ( x 0 , y 0 ) = ( 0 , 0 ) (x_0,y_0)=(0,0) ( x 0 , y 0 ) = ( 0 , 0 )
lim ( x , y ) → ( 0 , 0 ) f ( x , y ) − f ( 0 , 0 ) − f x ( 0 , 0 ) x − f y ( 0 , 0 ) y x 2 + y 2 \lim_{(x,y) \to (0,0)} \frac{f(x,y)-f(0,0)-f_x(0,0) x-f_y(0,0)y}{\sqrt{x^2+y^2}}
( x , y ) → ( 0 , 0 ) lim x 2 + y 2 f ( x , y ) − f ( 0 , 0 ) − f x ( 0 , 0 ) x − f y ( 0 , 0 ) y
这道题里面,偏导数等于 0 0 0 f ( 0 , 0 ) = 0 f(0,0)=0 f ( 0 , 0 ) = 0
lim r → 0 r cos θ sin θ r 2 ⋅ r sin r 2 = lim r → 0 cos θ sin θ \lim_{r \to 0} \frac{r\sqrt{\cos\theta\sin\theta}}{r^2\cdot r} \sin r^2=\lim_{r \to 0} \sqrt{\cos\theta\sin\theta}
r → 0 lim r 2 ⋅ r r cos θ sin θ sin r 2 = r → 0 lim cos θ sin θ
不存在,因此不可微。
定理
如果函数 f ( x , y ) f(x,y) f ( x , y ) ( x 0 , y 0 ) (x_0,y_0) ( x 0 , y 0 ) f ( x , y ) f(x,y) f ( x , y ) ( x 0 , y 0 ) (x_0,y_0) ( x 0 , y 0 ) f x ( x 0 , y 0 ) = A , f y ( x 0 , y 0 ) = B f_x(x_0,y_0)=A,f_y(x_0,y_0)=B f x ( x 0 , y 0 ) = A , f y ( x 0 , y 0 ) = B f ( x , y ) f(x,y) f ( x , y ) ( x 0 , y 0 ) (x_0,y_0) ( x 0 , y 0 )
d z ∣ ( x 0 , y 0 ) = f x ( x 0 , y 0 ) Δ x + f y ( x 0 , y 0 ) Δ y \boxed{\mathrm d z|_{(x_0,y_0)}=f_x(x_0,y_0)\Delta x+f_y(x_0,y_0)\Delta y}
d z ∣ ( x 0 , y 0 ) = f x ( x 0 , y 0 ) Δ x + f y ( x 0 , y 0 ) Δ y
d z = ∂ z ∂ x d x + ∂ z ∂ y d y \boxed{\mathrm d z=\frac{\partial z}{\partial x} \mathrm d x+\frac{\partial z}{\partial y}\mathrm d y}
d z = ∂ x ∂ z d x + ∂ y ∂ z d y
注意,前提是可微分,结论是全微分的形式。但是,证明全微分不存在,我们可以假设全微分存在,然后代入 f x , f y f_x,f_y f x , f y
可微分 ⇒ \Rightarrow ⇒
为什么?
先证明连续,连续等价为差为无穷小:
lim ( x , y ) → ( x 0 , y 0 ) Δ z \lim_{(x,y)\to(x_0,y_0)} \Delta z
( x , y ) → ( x 0 , y 0 ) lim Δ z
Δ z ≤ ∣ A ∣ ρ + ∣ B ∣ ρ + o ( ρ ) \Delta z \le |A|\rho+|B|\rho+o(\rho)
Δ z ≤ ∣ A ∣ ρ + ∣ B ∣ ρ + o ( ρ )
lim ( x , y ) → ( x 0 , y 0 ) Δ z ≤ lim ρ → 0 ∣ A ∣ ρ + ∣ B ∣ ρ + o ( ρ ) = 0 \lim_{(x,y)\to(x_0,y_0)} \Delta z\le \lim_{\rho \to 0}|A|\rho+|B|\rho+o(\rho)=0
( x , y ) → ( x 0 , y 0 ) lim Δ z ≤ ρ → 0 lim ∣ A ∣ ρ + ∣ B ∣ ρ + o ( ρ ) = 0
再证明偏导数存在且对应 A , B A,B A , B
∂ z ∂ x ∣ ( x 0 , y 0 ) = lim Δ x → 0 f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) Δ x = lim Δ x → 0 A Δ x + B × 0 + o ( ρ ) Δ x = A \left.\frac{\partial z}{\partial x}\right|_{(x_0,y_0)}=\lim_{\Delta x\to 0}\frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x}=\lim_{\Delta x\to 0}\frac{A\Delta x+B\times 0+o(\rho)}{\Delta x}=A
∂ x ∂ z ∣ ∣ ∣ ∣ ( x 0 , y 0 ) = Δ x → 0 lim Δ x f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) = Δ x → 0 lim Δ x A Δ x + B × 0 + o ( ρ ) = A
B B B
可微分的几何意义:对应一元函数可微分,函数在邻域内的值可被斜率为导数且过函数点的 直线 、切直线 拟合。二元函数可微分,函数在邻域内的值可被一个过函数点的 切平面 拟合。
这样,可以构造具有褶皱的平面,作为 f f f
注意,一元函数里面说连续不一定可微,但是可导和可微等价,推广到二元情况有所不同,是因为偏导数只是对 x = x 0 , y = y 0 x=x_0,y=y_0 x = x 0 , y = y 0
注意到,沿任何方向方向导数存在,也不一定可微,需要满足任意关系的 ( x , y ) → ( 0 , 0 ) (x,y) \to (0,0) ( x , y ) → ( 0 , 0 )
偏导数存在,然而不可全微分,可以将偏导数代入全微分的表达式,看看剩余的是不是 ρ \rho ρ
证明函数 f ( x , y ) = ∣ x y ∣ f(x,y)=\sqrt{|xy|} f ( x , y ) = ∣ x y ∣ ( 0 , 0 ) (0,0) ( 0 , 0 ) f x ( 0 , 0 ) , f y ( 0 , 0 ) f_x(0,0),f_y(0,0) f x ( 0 , 0 ) , f y ( 0 , 0 )
直观地理解:
偏导数存在:用平面取截函数图像,截出来的新函数可微。
可微:函数在这一点处趋于一个平面。
严格地证明:
显然,f ( x , y ) f(x,y) f ( x , y ) f x ( 0 , 0 ) = f y ( 0 , 0 ) = 0 f_x(0,0)=f_y(0,0)=0 f x ( 0 , 0 ) = f y ( 0 , 0 ) = 0
lim r → 0 r ∣ cos θ sin θ ∣ − 0 − 0 − 0 r = ∣ cos θ sin θ ∣ ≠ 0 \lim_{r \to 0}\frac{r\sqrt{|\cos \theta \sin \theta|}-0-0-0}{r}=\sqrt{|\cos \theta \sin \theta|} \not=0
r → 0 lim r r ∣ cos θ sin θ ∣ − 0 − 0 − 0 = ∣ cos θ sin θ ∣ = 0
因此不可微。
用变量代换的方法,设 y = k x y=kx y = k x
lim x → 0 , y → 0 ∣ x ∣ k ∣ x ∣ k 2 + 1 \lim_{x \to 0 ,y \to 0}\frac{|x|\sqrt{k}}{|x|\sqrt{k^2+1}}
x → 0 , y → 0 lim ∣ x ∣ k 2 + 1 ∣ x ∣ k
不存在,不可微。
若二元函数 f ( x , y ) f(x,y) f ( x , y ) ( 0 , 0 ) (0,0) ( 0 , 0 )
lim x → 0 , y → 0 f ( x , y ) g ( x , y ) = C \lim_{x\to0,y\to0} \frac{f(x,y)}{g(x,y)}=C
x → 0 , y → 0 lim g ( x , y ) f ( x , y ) = C
且
lim x → 0 , y → 0 g ( x , y ) x 2 + y 2 = 0 \lim_{x\to0,y\to0}\frac{g(x,y)}{\sqrt{x^2+y^2}}=0
x → 0 , y → 0 lim x 2 + y 2 g ( x , y ) = 0
则 f ( x , y ) f(x,y) f ( x , y ) ( 0 , 0 ) (0,0) ( 0 , 0 )
将极限乘起来即可。注意,这样可以一环套一环。因此,如果 g ( x , y ) g(x,y) g ( x , y ) lim x → 0 , y → 0 f ( x , y ) / g ( x , y ) = C \lim_{x\to0,y\to0} f(x,y)/g(x,y)=C lim x → 0 , y → 0 f ( x , y ) / g ( x , y ) = C f ( x , y ) f(x,y) f ( x , y )
定理:若函数 z = f ( x , y ) z=f(x,y) z = f ( x , y ) f x ( x , y ) , f y ( x , y ) f_x(x,y),f_y(x,y) f x ( x , y ) , f y ( x , y ) ( x 0 , y 0 ) (x_0,y_0) ( x 0 , y 0 ) f ( x , y ) f(x,y) f ( x , y )
但是可微不一定偏导函数连续。对应一元函数的情况:
f ( x ) = x sin 1 x , x ≠ 0 ; 0 , x = 0 f(x)=x\sin \frac{1}{x} ,x\not=0;0,x=0
f ( x ) = x sin x 1 , x = 0 ; 0 , x = 0
在 x = 0 x=0 x = 0
在 ( 0 , 0 ) (0,0) ( 0 , 0 )
f x , f y f_x,f_y f x , f y f f f
其实很多反例都可以从一元函数推出来:
全微分存在 ⇏ \not\Rightarrow ⇒ f ( x ) = x sin 1 x , x ≠ 0 ; 0 , x = 0 f(x)=x\sin \frac{1}{x} ,x\not=0;0,x=0 f ( x ) = x sin x 1 , x = 0 ; 0 , x = 0
函数连续 ⇏ \not\Rightarrow ⇒ f ( x ) = ∣ x ∣ f(x)=|x| f ( x ) = ∣ x ∣
偏导数存在 ⇏ \not\Rightarrow ⇒ f ( x , y ) = ∣ x y ∣ f(x,y)=\sqrt{|xy|} f ( x , y ) = ∣ x y ∣
偏导数存在 ⇏ \not\Rightarrow ⇒
函数连续 ⇏ \not\Rightarrow ⇒ f ( x ) = ∣ x ∣ f(x)=|x| f ( x ) = ∣ x ∣
全微分存在 ⇒ \Rightarrow ⇒

全微分的应用
f ( x , y ) ≈ f ( x 0 , y 0 ) + f x ( x 0 , y 0 ) ( x − x 0 ) + f y ( x 0 , y 0 ) ( y − y 0 ) f(x, y) \approx f\left(x_0, y_0\right)+f_x\left(x_0, y_0\right)\left(x-x_0\right)+f_y\left(x_0, y_0\right)\left(y-y_0\right)
f ( x , y ) ≈ f ( x 0 , y 0 ) + f x ( x 0 , y 0 ) ( x − x 0 ) + f y ( x 0 , y 0 ) ( y − y 0 )
设函数 u = φ ( x , y ) , v = ψ ( x , y ) u=\varphi(x, y), v=\psi(x, y) u = φ ( x , y ) , v = ψ ( x , y ) ( x , y ) (x, y) ( x , y ) z = f ( u , v ) z=f(u, v) z = f ( u , v ) ( u , v ) (u, v) ( u , v ) z = f [ φ ( x , y ) , ψ ( x , y ) ] z=f[\varphi(x, y), \psi(x, y)] z = f [ φ ( x , y ) , ψ ( x , y ) ] ( x , y ) (x, y) ( x , y )
∂ z ∂ x = ∂ z ∂ u ⋅ ∂ u ∂ x + ∂ z ∂ v ⋅ ∂ v ∂ x ; ∂ z ∂ y = ∂ z ∂ u ⋅ ∂ u ∂ y + ∂ z ∂ v ⋅ ∂ v ∂ y \frac{\partial z}{\partial x}=\frac{\partial z}{\partial u} \cdot \frac{\partial u}{\partial x}+\frac{\partial z}{\partial v} \cdot \frac{\partial v}{\partial x} ; \frac{\partial z}{\partial y}=\frac{\partial z}{\partial u} \cdot \frac{\partial u}{\partial y}+\frac{\partial z}{\partial v} \cdot \frac{\partial v}{\partial y}
∂ x ∂ z = ∂ u ∂ z ⋅ ∂ x ∂ u + ∂ v ∂ z ⋅ ∂ x ∂ v ; ∂ y ∂ z = ∂ u ∂ z ⋅ ∂ y ∂ u + ∂ v ∂ z ⋅ ∂ y ∂ v
上式称为多元复合函数偏导数的链式法则。
证明:利用可微和偏导数的定义:
lim Δ x → 0 Δ x z Δ x = ∂ z ∂ x \lim _{\Delta x \to 0}\frac{\Delta_x z}{\Delta x}=\frac{\partial z}{\partial x}
Δ x → 0 lim Δ x Δ x z = ∂ x ∂ z
令 Δ y = 0 \Delta y=0 Δ y = 0 Δ u = Δ x u , Δ v = Δ x v , ρ = ( Δ x u ) 2 + ( Δ x v ) 2 \Delta u=\Delta_x u,\Delta v=\Delta_x v,\rho=\sqrt{(\Delta_x u)^2+(\Delta_x v)^2} Δ u = Δ x u , Δ v = Δ x v , ρ = ( Δ x u ) 2 + ( Δ x v ) 2
得到:
Δ x z Δ x = ∂ z ∂ u ⋅ Δ x u Δ x + ∂ z ∂ v ⋅ Δ x v Δ x + o ( ρ ) Δ x \frac{\Delta_x z}{\Delta x}=\frac{\partial z}{\partial u} \cdot \frac{\Delta_x u}{\Delta x}+\frac{\partial z}{\partial v} \cdot \frac{\Delta_x v}{\Delta x}+\frac{o(\rho)}{\Delta x}
Δ x Δ x z = ∂ u ∂ z ⋅ Δ x Δ x u + ∂ v ∂ z ⋅ Δ x Δ x v + Δ x o ( ρ )
取 Δ x → 0 \Delta x \to 0 Δ x → 0
∂ z ∂ x = ∂ z ∂ u ⋅ ∂ u ∂ x + ∂ z ∂ v ⋅ ∂ v ∂ x \frac{\partial z}{\partial x}=\frac{\partial z}{\partial u} \cdot \frac{\partial u}{\partial x}+\frac{\partial z}{\partial v} \cdot \frac{\partial v}{\partial x}
∂ x ∂ z = ∂ u ∂ z ⋅ ∂ x ∂ u + ∂ v ∂ z ⋅ ∂ x ∂ v
思路:分析一个变量时,将其它变量看做常量
设 z = f ( x 2 − y 2 , 2 x y ) z=f\left(x^2-y^2, 2^{x y}\right) z = f ( x 2 − y 2 , 2 x y ) f f f ∂ z ∂ x , ∂ z ∂ y \frac{\partial z}{\partial x}, \frac{\partial z}{\partial y} ∂ x ∂ z , ∂ y ∂ z
z x = f 1 ⋅ 2 x + f 2 ⋅ y ⋅ 2 x y ln 2 ; z y = f 1 ⋅ ( − 2 y ) + f 2 ⋅ x ⋅ 2 x y ln 2 z_x=f_1 \cdot 2 x+f_2 \cdot y \cdot 2^{x y} \ln 2 ; z_y=f_1 \cdot(-2 y)+f_2 \cdot x \cdot 2^{x y} \ln 2
z x = f 1 ⋅ 2 x + f 2 ⋅ y ⋅ 2 x y ln 2 ; z y = f 1 ⋅ ( − 2 y ) + f 2 ⋅ x ⋅ 2 x y ln 2
设函数 z = f ( u , v ) , u = φ ( x ) , v = ψ ( x ) z=f(u, v), u=\varphi(x), v=\psi(x) z = f ( u , v ) , u = φ ( x ) , v = ψ ( x ) z = f [ φ ( x ) , ψ ( x ) ] z=f[\varphi(x), \psi(x)] z = f [ φ ( x ) , ψ ( x ) ] x x x
d z d x = ∂ z ∂ u ⋅ d u d x + ∂ z ∂ v ⋅ d v d x = ∂ z ∂ u ⋅ φ ′ ( x ) + ∂ z ∂ v ⋅ ψ ′ ( x ) \frac{\mathrm{d} z}{\mathrm{~d} x}=\frac{\partial z}{\partial u} \cdot \frac{\mathrm{d} u}{\mathrm{~d} x}+\frac{\partial z}{\partial v} \cdot \frac{\mathrm{d} v}{\mathrm{~d} x}=\frac{\partial z}{\partial u} \cdot \varphi^{\prime}(x)+\frac{\partial z}{\partial v} \cdot \psi^{\prime}(x)
d x d z = ∂ u ∂ z ⋅ d x d u + ∂ v ∂ z ⋅ d x d v = ∂ u ∂ z ⋅ φ ′ ( x ) + ∂ v ∂ z ⋅ ψ ′ ( x )
这个导数又称为全导数。
设函数 z = f ( u ) , u = φ ( x , y ) z=f(u), u=\varphi(x, y) z = f ( u ) , u = φ ( x , y ) z = f [ φ ( x , y ) ] z=f[\varphi(x, y)] z = f [ φ ( x , y ) ]
∂ z ∂ x = f ′ ( u ) ⋅ ∂ φ ∂ x ; ∂ z ∂ y = f ′ ( u ) ⋅ ∂ φ ∂ y \frac{\partial z}{\partial x}=f^{\prime}(u) \cdot \frac{\partial \varphi}{\partial x} ; \frac{\partial z}{\partial y}=f^{\prime}(u) \cdot \frac{\partial \varphi}{\partial y}
∂ x ∂ z = f ′ ( u ) ⋅ ∂ x ∂ φ ; ∂ y ∂ z = f ′ ( u ) ⋅ ∂ y ∂ φ
注意:中间变量只有一个时,函数对中间变量求导数。
设 x = u , y = u v x=u, y=u v x = u , y = u v u , v u, v u , v x ⋅ ∂ z ∂ x + y ⋅ ∂ z ∂ v = z \displaystyle x \cdot \frac{\partial z}{\partial x}+y \cdot \frac{\partial z}{\partial v}=z x ⋅ ∂ x ∂ z + y ⋅ ∂ v ∂ z = z
解法一:
∂ z ∂ u = ∂ z ∂ x ⋅ ∂ x ∂ u + ∂ z ∂ y ⋅ ∂ y ∂ u = ∂ z ∂ x ⋅ 1 + ∂ z ∂ y ⋅ v \frac{\partial z}{\partial u}=\frac{\partial z}{\partial x} \cdot \frac{\partial x}{\partial u}+\frac{\partial z}{\partial y} \cdot \frac{\partial y}{\partial u}=\frac{\partial z}{\partial x} \cdot 1+\frac{\partial z}{\partial y} \cdot v
∂ u ∂ z = ∂ x ∂ z ⋅ ∂ u ∂ x + ∂ y ∂ z ⋅ ∂ u ∂ y = ∂ x ∂ z ⋅ 1 + ∂ y ∂ z ⋅ v
∂ z ∂ v = ∂ z ∂ x ⋅ ∂ x ∂ v + ∂ z ∂ y ⋅ ∂ y ∂ v = ∂ z ∂ x ⋅ 0 + ∂ z ∂ y ⋅ u \frac{\partial z}{\partial v}=\frac{\partial z}{\partial x} \cdot \frac{\partial x}{\partial v}+\frac{\partial z}{\partial y} \cdot \frac{\partial y}{\partial v}=\frac{\partial z}{\partial x} \cdot 0+\frac{\partial z}{\partial y} \cdot u
∂ v ∂ z = ∂ x ∂ z ⋅ ∂ v ∂ x + ∂ y ∂ z ⋅ ∂ v ∂ y = ∂ x ∂ z ⋅ 0 + ∂ y ∂ z ⋅ u
然后解出 ∂ z ∂ x , ∂ z ∂ y \frac{\partial z}{\partial x}, \frac{\partial z}{\partial y} ∂ x ∂ z , ∂ y ∂ z u ⋅ ∂ z ∂ u = z u \cdot \frac{\partial z}{\partial u}=z u ⋅ ∂ u ∂ z = z
设二元函数 z = z ( x , y ) z=z(x, y) z = z ( x , y ) D D D u = x y , v = x + y u=\frac{x}{y}, v=x+y u = y x , v = x + y z = z ( x , y ) z=z(x, y) z = z ( x , y ) D D D z = f ( x y ) z=f\left(\frac{x}{y}\right) z = f ( y x ) x ⋅ ∂ z ∂ x + y ⋅ ∂ z ∂ v = 0 x \cdot \frac{\partial z}{\partial x}+y \cdot \frac{\partial z}{\partial v}=0 x ⋅ ∂ x ∂ z + y ⋅ ∂ v ∂ z = 0
反向证明:需要 ∂ z / ∂ v = 0 \partial z/\partial v=0 ∂ z / ∂ v = 0
设函数 z = f ( x , y ) z=f(x, y) z = f ( x , y ) ( 1 , 1 ) (1,1) ( 1 , 1 ) f ( 1 , 1 ) = 1 , f x ( 1 , 1 ) = 2 , f y ( 1 , 1 ) = 3 f(1,1)=1, f_x(1,1)=2, f_y(1,1)=3 f ( 1 , 1 ) = 1 , f x ( 1 , 1 ) = 2 , f y ( 1 , 1 ) = 3 φ ( x ) = f [ x , f ( x , x ) ] \varphi(x)=f[x, f(x, x)] φ ( x ) = f [ x , f ( x , x ) ] d [ φ 2 ( x ) ] d x ∣ x = 1 \displaystyle \left.\frac{\mathrm{d}\left[\varphi^2(x)\right]}{\mathrm{d} x}\right|_{x=1} d x d [ φ 2 ( x ) ] ∣ ∣ ∣ ∣ ∣ x = 1 d [ φ 2 ( x ) ] d x ∣ x = 1 = 2 φ ( 1 ) ⋅ φ ′ ( 1 ) \displaystyle \left.\frac{\mathrm{d}\left[\varphi^2(x)\right]}{\mathrm{d} x}\right|_{x=1}=2 \varphi(1) \cdot \varphi^{\prime}(1) d x d [ φ 2 ( x ) ] ∣ ∣ ∣ ∣ ∣ x = 1 = 2 φ ( 1 ) ⋅ φ ′ ( 1 ) φ ( 1 ) = f [ 1 , f ( 1 , 1 ) ] = f ( 1 , 1 ) = 1 \varphi(1)=f[1, f(1,1)]=f(1,1)=1 φ ( 1 ) = f [ 1 , f ( 1 , 1 ) ] = f ( 1 , 1 ) = 1 φ ′ ( x ) = f 1 [ x , f ( x , x ) ] ⋅ 1 + f 2 [ x , f ( x , x ) ] ⋅ [ f 1 ( x , x ) ⋅ 1 + f 2 ( x , x ) ⋅ 1 ] \varphi^{\prime}(x)=f_1[x, f(x, x)] \cdot 1+f_2[x, f(x, x)] \cdot\left[f_1(x, x) \cdot 1+f_2(x, x) \cdot 1\right] φ ′ ( x ) = f 1 [ x , f ( x , x ) ] ⋅ 1 + f 2 [ x , f ( x , x ) ] ⋅ [ f 1 ( x , x ) ⋅ 1 + f 2 ( x , x ) ⋅ 1 ] φ ′ ( 1 ) = f 1 ( 1 , 1 ) + f 2 ( 1 , 1 ) ⋅ [ f 1 ( 1 , 1 ) + f 2 ( 1 , 1 ) ] = 17 \varphi^{\prime}(\mathbf{1})=f_1(1,1)+f_2(1,1) \cdot\left[f_1(1,1)+f_2(1,1)\right]=17 φ ′ ( 1 ) = f 1 ( 1 , 1 ) + f 2 ( 1 , 1 ) ⋅ [ f 1 ( 1 , 1 ) + f 2 ( 1 , 1 ) ] = 1 7
偏导数下标代表对第 i i i f 2 [ x , f ( x , x ) ] f_2[x, f(x, x)] f 2 [ x , f ( x , x ) ] f [ x , f ( x , x ) ] f[x, f(x, x)] f [ x , f ( x , x ) ] f ( x , x ) f(x,x) f ( x , x )
z x = f u u x + f v v x ; z y = f u u y + f v v y z_x=f_uu_x+f_vv_x;z_y=f_uu_y+f_vv_y
z x = f u u x + f v v x ; z y = f u u y + f v v y
( z x ) x = ( f u u u x + f u v v x ) u x + f u u x x + ( f v u u x + f v v v x ) v x + f v v x x (z_x)_x=(f_{uu}u_x+f_{uv}v_x)u_x+f_uu_{xx}+(f_{vu}u_x+f_{vv}v_x)v_x+f_vv_{xx}
( z x ) x = ( f u u u x + f u v v x ) u x + f u u x x + ( f v u u x + f v v v x ) v x + f v v x x
设 z = f ( x 2 y , x y 2 ) z=f(x^2y,\frac{x}{y^2}) z = f ( x 2 y , y 2 x ) ∂ 2 z ∂ x ∂ y \frac{\partial^2 z}{\partial x\partial y} ∂ x ∂ y ∂ 2 z
∂ z ∂ x = f u 2 x y + f v 1 y 2 \frac{\partial z}{\partial x}=f_u 2xy+f_v\frac{1}{y^2}
∂ x ∂ z = f u 2 x y + f v y 2 1
∂ 2 z ∂ x ∂ y = 2 x f u + 2 x y ( f u u x 2 + f u v ( − 2 x 2 y 3 ) ) − 2 y 2 f v + 1 y 2 ( f v u x 2 + f v v ( − 2 x 2 y 3 ) ) \frac{\partial^2 z}{\partial x\partial y}=2xf_u+2xy\left(f_{uu}x^2+f_{uv}\left(-\frac{2x^2}{y^3}\right)\right)-\frac{2}{y^2}f_v+\frac{1}{y^2}\left(f_{vu}x^2+f_{vv}\left(-\frac{2x^2}{y^3}\right)\right)
∂ x ∂ y ∂ 2 z = 2 x f u + 2 x y ( f u u x 2 + f u v ( − y 3 2 x 2 ) ) − y 2 2 f v + y 2 1 ( f v u x 2 + f v v ( − y 3 2 x 2 ) )
注:z x y ( 1 , 1 ) ≠ ( z x ( 1 , 1 ) ) y z_{xy}(1,1)\not=(z_x(1,1))_y z x y ( 1 , 1 ) = ( z x ( 1 , 1 ) ) y
设 y = f ( u ) , u = φ ( x ) y=f(u), u=\varphi(x) y = f ( u ) , u = φ ( x ) y = f [ φ ( x ) ] y=f[\varphi(x)] y = f [ φ ( x ) ] d y = [ f ′ ( u ) ⋅ φ ′ ( x ) ] d x = f ′ ( u ) ⋅ [ φ ′ ( x ) d x ] = f ′ ( u ) ⋅ d u \mathrm{d} y=\left[f^{\prime}(u) \cdot \varphi^{\prime}(x)\right] \mathrm{d} x=f^{\prime}(u) \cdot\left[\varphi^{\prime}(x) \mathrm{d} x\right]=f^{\prime}(u) \cdot \mathrm{d} u d y = [ f ′ ( u ) ⋅ φ ′ ( x ) ] d x = f ′ ( u ) ⋅ [ φ ′ ( x ) d x ] = f ′ ( u ) ⋅ d u u u u
y = f ( u ) ⇒ d y = f ′ ( u ) ⋅ d u 。 y=f(u) \Rightarrow \mathrm{d} y=f^{\prime}(u) \cdot \mathrm{d} u \text { 。 }
y = f ( u ) ⇒ d y = f ′ ( u ) ⋅ d u 。
这就是一元函数的一阶微分形式不变性。
变量代换形成的方程,其基本思路是通过特殊的变量代换,使得方程形式简化,或者和某个变量无关。
也就是说,如果 u = f ( x , y , z ) u=f(x,y,z) u = f ( x , y , z )
∂ u ∂ z = 0 \frac{\partial u}{\partial z}=0
∂ z ∂ u = 0
则 u = g ( x , y ) u=g(x,y) u = g ( x , y )
设定义在平面上的函数 u ( x , y ) u(x,y) u ( x , y )
证明 ( x 2 + y 2 ) ( u x x + u y y ) = r 2 ∂ 2 u ∂ r 2 + r ∂ u ∂ r + ∂ 2 u ∂ θ 2 (x^2+y^2)(u_{xx}+u_{yy})=r^2 \frac{\partial^2 u}{\partial r^2}+r\frac{\partial u}{\partial r}+\frac{\partial^2 u}{\partial \theta^2} ( x 2 + y 2 ) ( u x x + u y y ) = r 2 ∂ r 2 ∂ 2 u + r ∂ r ∂ u + ∂ θ 2 ∂ 2 u x = r cos θ , y = r sin θ x=r\cos \theta, y=r\sin \theta x = r cos θ , y = r sin θ
需要结合结论和推导来做。
原式变为 u x x + u y y = ∂ 2 u ∂ r 2 + ( u x cos θ + u y sin θ ) ( 1 − 1 r 2 ) + u x x sin 2 θ + u y y cos 2 θ u_{xx}+u_{yy}=\frac{\partial^2 u}{\partial r^2}+(u_x \cos \theta+u_y \sin \theta)(1-\frac{1}{r^2})+u_{xx}\sin^2\theta+u_{yy}\cos^2\theta u x x + u y y = ∂ r 2 ∂ 2 u + ( u x cos θ + u y sin θ ) ( 1 − r 2 1 ) + u x x sin 2 θ + u y y cos 2 θ
常见的形式:
x ∂ f ∂ x + y ∂ f ∂ y x\frac{\partial f}{\partial x}+y \frac{\partial f}{\partial y}
x ∂ x ∂ f + y ∂ y ∂ f
实际上,需要引入新的变量 t t t
u = f ( t x , t y ) ∂ u ∂ t = x ∂ f ∂ x + y ∂ f ∂ y u=f(tx,ty)\\
\frac{\partial u}{\partial t}=x\frac{\partial f}{\partial x}+y\frac{\partial f}{\partial y}
u = f ( t x , t y ) ∂ t ∂ u = x ∂ x ∂ f + y ∂ y ∂ f
还可以这么看:这相当于 ∇ f ⋅ ( x , y ) = 0 \nabla f \cdot (x,y)=0 ∇ f ⋅ ( x , y ) = 0 ( x , y ) (x,y) ( x , y ) L : x = a t , y = b t L:x=at,y=bt L : x = a t , y = b t
设 f ( x , y ) f(x,y) f ( x , y ) R 2 \R^2 R 2 lim r → + ∞ ( x ∂ f ∂ x + y ∂ f ∂ y ) = 1 \displaystyle \lim_{r \to +\infin} (x\frac{\partial f}{\partial x}+y\frac{\partial f}{\partial y})=1 r → + ∞ lim ( x ∂ x ∂ f + y ∂ y ∂ f ) = 1 r = x 2 + y 2 r=\sqrt{x^2+y^2} r = x 2 + y 2 f ( x , y ) f(x,y) f ( x , y ) R 2 \R^2 R 2
代换 x = r cos θ , y = r sin θ x=r\cos \theta,y=r\sin \theta x = r cos θ , y = r sin θ u = f ( x , y ) = f ( r cos θ , r sin θ ) u=f(x,y)=f(r\cos \theta,r\sin \theta) u = f ( x , y ) = f ( r cos θ , r sin θ )
lim r → + ∞ ∂ u ∂ t = 1 \lim_{r \to +\infin }\frac{\partial u}{\partial t}=1
r → + ∞ lim ∂ t ∂ u = 1
设函数 z = f ( x , y ) z=f(x, y) z = f ( x , y ) x ∂ f ∂ x + y ∂ f ∂ y = 0 x \frac{\partial f}{\partial x}+y \frac{\partial f}{\partial y}=0 x ∂ x ∂ f + y ∂ y ∂ f = 0 f ( x , y ) f(x, y) f ( x , y ) 证 x ∂ f ∂ x + y ∂ f ∂ y = 0 ⇒ x f x ( x , y ) + y f y ( x , y ) = 0 ⇒ t x f x ( t x , t y ) + t y f y ( t x , t y ) = 0 , ( t > 0 ) ⇒ x f x ( t x , t y ) + y f y ( t x , t y ) = 0 , ( t > 0 ) \begin{aligned} \text { 证 } & x \frac{\partial f}{\partial x}+y \frac{\partial f}{\partial y}=0 \Rightarrow x f_x(x, y)+y f_y(x, y)=0 \\ \Rightarrow & t x f_x(t x, t y)+t y f_y(t x, t y)=0,(t>0) \\ \Rightarrow & x f_x(t x, t y)+y f_y(t x, t y)=0,(t>0)\end{aligned}
证 ⇒ ⇒ x ∂ x ∂ f + y ∂ y ∂ f = 0 ⇒ x f x ( x , y ) + y f y ( x , y ) = 0 t x f x ( t x , t y ) + t y f y ( t x , t y ) = 0 , ( t > 0 ) x f x ( t x , t y ) + y f y ( t x , t y ) = 0 , ( t > 0 )
⇒ d d t f ( t x , t y ) = 0 , ( t > 0 ) ⇒ f ( t x , t y ) = c ( x , y ) , ( t > 0 ) \begin{aligned}
& \Rightarrow \quad \frac{d}{d t} f(t x, t y)=0,(t>0) \\
& \Rightarrow \quad f(t x, t y)=c(x, y),(t>0) \\
\end{aligned}
⇒ d t d f ( t x , t y ) = 0 , ( t > 0 ) ⇒ f ( t x , t y ) = c ( x , y ) , ( t > 0 )
令 t → 0 + t \to 0^+ t → 0 + c ( x , y ) = f ( 0 , 0 ) c(x,y)=f(0,0) c ( x , y ) = f ( 0 , 0 )
f ( t x , t y ) = f ( 0 , 0 ) , ( t > 0 ) f(tx,ty)=f(0,0),(t>0)
f ( t x , t y ) = f ( 0 , 0 ) , ( t > 0 )
取 t = 1 t=1 t = 1
f ( x , y ) = f ( 0 , 0 ) f(x,y)=f(0,0)
f ( x , y ) = f ( 0 , 0 )
z = f ( x , y ) z=f(x,y) z = f ( x , y ) 3 ∂ z ∂ x − 2 ∂ z ∂ y = 0 3 \frac{\partial z}{\partial x}-2\frac{\partial z}{\partial y}=0 3 ∂ x ∂ z − 2 ∂ y ∂ z = 0
在变量替换 u = 2 x + 3 y ; v = x − y u=2x+3y;v=x-y u = 2 x + 3 y ; v = x − y z z z u , v u,v u , v
∂ z ∂ v = 0 \frac{\partial z}{\partial v}=0
∂ v ∂ z = 0
z = z ( u , v ) z=z(u,v) z = z ( u , v ) u u u z z z u u u
构造函数 f ( x , y , r 2 − x 2 − y 2 ) f(x,y,\sqrt{r^2-x^2-y^2}) f ( x , y , r 2 − x 2 − y 2 ) f f f x , y x,y x , y
隐函数存在定理 F ( x , y ) F(x, y) F ( x , y ) M 0 ( x 0 , y 0 ) M_0\left(x_0, y_0\right) M 0 ( x 0 , y 0 ) 连续偏导数 , 且 ∗ F ( x 0 , y 0 ) = 0 , ∗ F y ( x 0 , y 0 ) ≠ 0 *F\left(x_0, y_0\right)=0, *F_y\left(x_0, y_0\right) \neq 0 ∗ F ( x 0 , y 0 ) = 0 , ∗ F y ( x 0 , y 0 ) = 0 F ( x , y ) = 0 F(x, y)=0 F ( x , y ) = 0 M 0 M_0 M 0 y = y ( x ) y=y(x) y = y ( x ) F ( x 0 , y 0 ) = 0 , y 0 = y ( x 0 ) F\left(x_0, y_0\right)=0, y_0=y\left(x_0\right) F ( x 0 , y 0 ) = 0 , y 0 = y ( x 0 ) 连续的导数 d y d x = − F x ( x , y ) F y ( x , y ) \frac{\mathrm{d} y}{\mathrm{~d} x}=-\frac{F_x(x, y)}{F_y(x, y)} d x d y = − F y ( x , y ) F x ( x , y )
d y F y ( x , y ) + d x F x ( x , y ) = 0 \mathrm{d} y F_y(x,y)+\mathrm d xF_x(x,y)=0
d y F y ( x , y ) + d x F x ( x , y ) = 0
隐函数:确定函数 y = y ( x ) y=y(x) y = y ( x )
判断是否能够确定隐函数,需要满足带进去点值成立,而且不能有多个点同时满足。然后就是导数存在。
设两个函数 F ( x , y , u , v ) , G ( x , y , u , v ) F(x, y, u, v), G(x, y, u, v) F ( x , y , u , v ) , G ( x , y , u , v ) M 0 ( x 0 , y 0 , u 0 , v 0 ) M_0\left(x_0, y_0, u_0, v_0\right) M 0 ( x 0 , y 0 , u 0 , v 0 ) F ( x 0 , y 0 , u 0 , v 0 ) = 0 , G ( x 0 , y 0 , u 0 , v 0 ) = 0 F\left(x_0, y_0, u_0, v_0\right)=0, G\left(x_0, y_0, u_0, v_0\right)=0 F ( x 0 , y 0 , u 0 , v 0 ) = 0 , G ( x 0 , y 0 , u 0 , v 0 ) = 0 { F ( x , y , u , v ) = 0 G ( x , y , u , v ) = 0 \left\{\begin{array}{l}F(x, y, u, v)=0 \\ G(x, y, u, v)=0\end{array}\right. { F ( x , y , u , v ) = 0 G ( x , y , u , v ) = 0 M 0 M_0 M 0
这个方程组确定了两个二元函数 u = u ( x , y ) , v = v ( x , y ) u=u(x,y),v=v(x,y) u = u ( x , y ) , v = v ( x , y )
{ F x + F u u x + F v v x = 0 G x + G u u x + G v v x = 0 \left\{\begin{array}{l}F_x+F_uu_x+F_vv_x=0 \\ G_x+G_uu_x+G_vv_x=0\end{array}\right.
{ F x + F u u x + F v v x = 0 G x + G u u x + G v v x = 0
解得:
u x = − ∣ F x F v G x G v ∣ ∣ F u F v G u G v ∣ v x = − ∣ F u F x G u G x ∣ ∣ F u F v G u G v ∣ u_x=-\frac{\begin{vmatrix}F_x
& F_v\\G_x&G_v\end{vmatrix}}{\begin{vmatrix}F_u
& F_v\\G_u&G_v\end{vmatrix}} \quad v_x=-\frac{\begin{vmatrix}F_u
& F_x\\G_u&G_x\end{vmatrix}}{\begin{vmatrix}F_u
& F_v\\G_u&G_v\end{vmatrix}}
u x = − ∣ ∣ ∣ ∣ F u G u F v G v ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ F x G x F v G v ∣ ∣ ∣ ∣ v x = − ∣ ∣ ∣ ∣ F u G u F v G v ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ F u G u F x G x ∣ ∣ ∣ ∣
方法:如果是 a b a_b a b a a a b b b
设 y = f ( x , t ) y=f(x,t) y = f ( x , t ) t = t ( x , y ) t=t(x,y) t = t ( x , y ) F ( x , y , t ) = 0 F(x,y,t)=0 F ( x , y , t ) = 0 d y / d x \mathrm d y/\mathrm d x d y / d x
方法一:
d y = f 1 ⋅ d x + f 2 ⋅ d t \mathrm d y=f_1 \cdot \mathrm d x+f_2 \cdot \mathrm d t
d y = f 1 ⋅ d x + f 2 ⋅ d t
而 d t = t 1 ⋅ d x + t 2 ⋅ d y \mathrm d t=t_1 \cdot \mathrm d x+t_2 \cdot \mathrm d y d t = t 1 ⋅ d x + t 2 ⋅ d y
得到:
d y d x = f 1 + f 2 t 1 1 − t 2 \frac{\mathrm d y}{\mathrm d x}=\frac{f_1+f_2 t_1}{1-t_2}
d x d y = 1 − t 2 f 1 + f 2 t 1
注意到 f 1 f_1 f 1 f 2 f_2 f 2 f f f t 1 t_1 t 1 t 2 t_2 t 2 t t t x , y x,y x , y t t t t 1 = − F 1 F 3 , t 2 = − F 2 F 3 t_1=-\frac{F_1}{F_3},t_2=-\frac{F_2}{F_3} t 1 = − F 3 F 1 , t 2 = − F 3 F 2
方法二:
直接把问题看成由两个方程确定的隐函数,
{ F ( x , y , t ) = 0 G ( x , y , t ) = y − f ( x , t ) = 0 \left\{\begin{array}{c}
F(x, y, t)=0 \\
G(x, y, t)=y-f(x, t)=0
\end{array}\right.
{ F ( x , y , t ) = 0 G ( x , y , t ) = y − f ( x , t ) = 0
由计算公式得 d y d x = − 1 J ∂ ( F , G ) ∂ ( x , t ) \frac{\mathrm{d} y}{\mathrm{~d} x}=-\frac{1}{J} \frac{\partial(F, G)}{\partial(x, t)} d x d y = − J 1 ∂ ( x , t ) ∂ ( F , G )
J = ∂ ( F , G ) ∂ ( y , t ) = ∣ F y F t G y G t ∣ = F y ⋅ ( − f t ) − F t ⋅ 1 , J=\frac{\partial(F, G)}{\partial(y, t)}=\left|\begin{array}{ll}
F_y & F_t \\
G_y & G_t
\end{array}\right|=F_y \cdot\left(-f_t\right)-F_t \cdot 1,
J = ∂ ( y , t ) ∂ ( F , G ) = ∣ ∣ ∣ ∣ F y G y F t G t ∣ ∣ ∣ ∣ = F y ⋅ ( − f t ) − F t ⋅ 1 ,
可得: d y d x = − F x ⋅ ( − f t ) − F t ⋅ ( − f x ) F y ⋅ ( − f t ) − F t ⋅ 1 \frac{\mathrm{d} y}{\mathrm{~d} x}=-\frac{F_x \cdot\left(-f_t\right)-F_t \cdot\left(-f_x\right)}{F_y \cdot\left(-f_t\right)-F_t \cdot 1} d x d y = − F y ⋅ ( − f t ) − F t ⋅ 1 F x ⋅ ( − f t ) − F t ⋅ ( − f x )
(分清自变量和因变量,对……求偏导,……就是自变量)
通常计算隐函数的二阶偏导数不用公式。而计算隐函数的一阶偏导数可直接利用公式。
方向导数的定义:
设函数 z = f ( x , y ) z=f(x, y) z = f ( x , y ) M 0 ( x 0 , y 0 ) M_0\left(x_0, y_0\right) M 0 ( x 0 , y 0 ) l \boldsymbol l l cos α , cos β \cos \alpha, \cos \beta cos α , cos β
lim t → 0 f ( x 0 + t cos α , y 0 + t cos β ) − f ( x 0 , y 0 ) t \lim _{t \rightarrow 0} \frac{f\left(x_0+t \cos \alpha, y_0+t \cos \beta\right)-f\left(x_0, y_0\right)}{t}
t → 0 lim t f ( x 0 + t cos α , y 0 + t cos β ) − f ( x 0 , y 0 )
存在,则称此极限值为函数 z = f ( x , y ) z=f(x, y) z = f ( x , y ) M 0 M_0 M 0 l \boldsymbol l l ∂ z ∂ l ∣ ( x 0 , y 0 ) \displaystyle \left.\frac{\partial z}{\partial \boldsymbol l}\right|_{\left(x_0, y_0\right)} ∂ l ∂ z ∣ ∣ ∣ ∣ ( x 0 , y 0 ) ∂ f ∂ l ∣ ( x 0 , y 0 ) \displaystyle \left.\frac{\partial f}{\partial \boldsymbol l}\right|_{\left(x_0, y_0\right)} ∂ l ∂ f ∣ ∣ ∣ ∣ ( x 0 , y 0 )
方向导数的定义和偏导数的定义的对比。自变量只有 t t t Δ y \Delta y Δ y
交大课本上的是双向的方向导数,因此 x , y x,y x , y
方向余弦:平方和为 1
特殊的情况,当 l ⃗ = { 1 , 0 } \vec{l}=\{1,0\} l = { 1 , 0 } x x x
∂ z ∂ x ∣ ( x 0 , y 0 ) \left.\frac{\partial z}{\partial x}\right|_{\left(x_0, y_0\right)}
∂ x ∂ z ∣ ∣ ∣ ∣ ( x 0 , y 0 )
方向导数的计算:
设函数 z = f ( x , y ) z=f(x, y) z = f ( x , y ) M 0 ( x 0 , y 0 ) M_0\left(x_0, y_0\right) M 0 ( x 0 , y 0 ) ,l l l cos α , cos β \cos \alpha, \cos \beta cos α , cos β z = f ( x , y ) z=f(x, y) z = f ( x , y ) M 0 M_0 M 0 l ⃗ \vec{l} l
∂ z ∂ l ∣ ( x 0 , y 0 ) = f x ( x 0 , y 0 ) cos α + f y ( x 0 , y 0 ) cos β \left.\frac{\partial z}{\partial l}\right|_{\left(x_0, y_0\right)}=f_x\left(x_0, y_0\right) \cos \alpha+f_y\left(x_0, y_0\right) \cos \beta
∂ l ∂ z ∣ ∣ ∣ ∣ ( x 0 , y 0 ) = f x ( x 0 , y 0 ) cos α + f y ( x 0 , y 0 ) cos β
证明:由于函数 z = f ( x , y ) z=f(x, y) z = f ( x , y ) M 0 ( x 0 , y 0 ) M_0\left(x_0, y_0\right) M 0 ( x 0 , y 0 )
f ( x 0 + t cos α , y 0 + t cos β ) − f ( x 0 , y 0 ) = f x ( x 0 , y 0 ) ⋅ t cos α + f y ( x 0 , y 0 ) ⋅ t cos β + o ( t ) f\left(x_0+t \cos \alpha, y_0+t \cos \beta\right)-f\left(x_0, y_0\right)=f_x\left(x_0, y_0\right) \cdot t \cos \alpha+f_y\left(x_0, y_0\right) \cdot t \cos \beta+o(t)
f ( x 0 + t cos α , y 0 + t cos β ) − f ( x 0 , y 0 ) = f x ( x 0 , y 0 ) ⋅ t cos α + f y ( x 0 , y 0 ) ⋅ t cos β + o ( t )
而
lim t → 0 f ( x 0 + t cos α , y 0 + t cos β ) − f ( x 0 , y 0 ) t = f x ( x 0 , y 0 ) cos α + f y ( x 0 , y 0 ) cos β \begin{aligned}
&\lim _{t \rightarrow 0} \frac{f\left(x_0+t \cos \alpha, y_0+t \cos \beta\right)-f\left(x_0, y_0\right)}{t}\\
=&f_x\left(x_0, y_0\right) \cos \alpha+f_y\left(x_0, y_0\right) \cos \beta
\end{aligned}
= t → 0 lim t f ( x 0 + t cos α , y 0 + t cos β ) − f ( x 0 , y 0 ) f x ( x 0 , y 0 ) cos α + f y ( x 0 , y 0 ) cos β
因此, ∂ z ∂ l ∣ ( x 0 , y 0 ) = f x ( x 0 , y 0 ) cos α + f y ( x 0 , y 0 ) cos β \frac{\partial z}{\left.\partial l \right|_{\left(x_0, y_0\right)}}=f_x\left(x_0, y_0\right) \cos \alpha+f_y\left(x_0, y_0\right) \cos \beta ∂ l ∣ ( x 0 , y 0 ) ∂ z = f x ( x 0 , y 0 ) cos α + f y ( x 0 , y 0 ) cos β
设函数 z = f ( x , y ) z=f(x,y) z = f ( x , y ) D D D 可微 ,对于每一点 M 0 ( x 0 , y 0 ) ∈ D M_0(x_0,y_0) \in D M 0 ( x 0 , y 0 ) ∈ D z = f ( x , y ) z=f(x,y) z = f ( x , y ) M 0 M_0 M 0 方向 ,其模为函数 z = f ( x , y ) z=f(x,y) z = f ( x , y ) M 0 M_0 M 0 z = f ( x , y ) z=f(x,y) z = f ( x , y ) M 0 M_0 M 0 grad f ∣ ( x 0 , y 0 ) \operatorname{grad} f\mid_{(x_0,y_0)} g r a d f ∣ ( x 0 , y 0 ) grad f ( x 0 , y 0 ) \operatorname{grad} f(x_0,y_0) g r a d f ( x 0 , y 0 )
证明:相当于向量的点乘,当夹角为 0 0 0 π \pi π
得出结论:
max l ∂ z ∂ l ∣ ( a , b ) = = = l = ∇ z ∣ ∇ z ∣ ( a , b ) \boxed{\max_\boldsymbol l \left.\frac{\partial z}{\partial \boldsymbol l}\right|_{(a,b)}\overset{\boldsymbol l=\nabla z}{=\!=\!=}|\nabla z|_{(a,b)}}
l max ∂ l ∂ z ∣ ∣ ∣ ∣ ( a , b ) = = = l = ∇ z ∣ ∇ z ∣ ( a , b )
记 ∇ = { ∂ ∂ x , ∂ ∂ y } \nabla = \{\frac{\partial}{\partial x},\frac{\partial}{\partial y}\} ∇ = { ∂ x ∂ , ∂ y ∂ } ∇ \nabla ∇ z = f ( x , y ) z=f(x,y) z = f ( x , y ) M 0 M_0 M 0
∇ f ∣ ( x 0 , y 0 ) , ∇ f ( x 0 , y 0 ) \nabla f|_{(x_0,y_0)},\nabla f(x_0,y_0)
∇ f ∣ ( x 0 , y 0 ) , ∇ f ( x 0 , y 0 )
推论:方向导数的最大值为 ∣ ∣ ∇ f ( x 0 , y 0 ) ∣ ∣ ||\nabla f(x_0,y_0)|| ∣ ∣ ∇ f ( x 0 , y 0 ) ∣ ∣ − ∣ ∣ ∇ f ( x 0 , y 0 ) ∣ ∣ -||\nabla f(x_0,y_0)|| − ∣ ∣ ∇ f ( x 0 , y 0 ) ∣ ∣
梯度的运算性质,和微分和偏微分相同,证明关注每一维即可。
∇ ( k 1 u + k 2 v ) = k 1 ∇ u + k 2 ∇ v \nabla\left(k_1 u+k_2 v\right)=k_1 \nabla u+k_2 \nabla v ∇ ( k 1 u + k 2 v ) = k 1 ∇ u + k 2 ∇ v k 1 , k 2 k_1, k_2 k 1 , k 2
∇ ( u ⋅ v ) = v ⋅ ∇ u + u ⋅ ∇ v ∇ ( u v ) = v ⋅ ∇ u − u ⋅ ∇ v v 2 ∇ f ( u ) = f ′ ( u ) ∇ u ; ∇ g ( u , v ) = g u ⋅ ∇ u + g v ⋅ ∇ v 。 \begin{aligned}
& \nabla(u \cdot v)=v \cdot \nabla u+u \cdot \nabla v \\
& \nabla\left(\frac{u}{v}\right)=\frac{v \cdot \nabla u-u \cdot \nabla v}{v^2} \\
& \nabla f(u)=f^{\prime}(u) \nabla u ; \nabla g(u, v)=g_u \cdot \nabla u+g_v \cdot \nabla v 。
\end{aligned}
∇ ( u ⋅ v ) = v ⋅ ∇ u + u ⋅ ∇ v ∇ ( v u ) = v 2 v ⋅ ∇ u − u ⋅ ∇ v ∇ f ( u ) = f ′ ( u ) ∇ u ; ∇ g ( u , v ) = g u ⋅ ∇ u + g v ⋅ ∇ v 。
方向导数与梯度的关系:
∂ f ∂ l ∣ ( x 0 , y 0 ) = ∇ f ∣ ( x 0 , y 0 ) ⋅ l 0 \boxed{\left.\frac{\partial f}{\partial \boldsymbol{l}} \right|_{(x_0,y_0)} =\nabla f|_{(x_0,y_0)} \cdot \boldsymbol{l}^0}
∂ l ∂ f ∣ ∣ ∣ ∣ ( x 0 , y 0 ) = ∇ f ∣ ( x 0 , y 0 ) ⋅ l 0
∇ f ∣ ( x 0 , y 0 ) \nabla f|_{(x_0,y_0)} ∇ f ∣ ( x 0 , y 0 )

连续的一阶偏导数告诉我们可微,因此,任意一点存在方向导数,而且可以通过方向导数近似。如果是闭区间,必然存在极值,利用 grad f ≠ 0 \operatorname{grad} f\not=0 g r a d f = 0 Δ f ≡ 0 \Delta f\equiv0 Δ f ≡ 0 f x = f y = 0 f_x=f_y=0 f x = f y = 0
还是利用 grad f ≠ 0 \operatorname{grad} f\not=0 g r a d f = 0
grad f \operatorname{grad} f g r a d f
回顾空间曲面
空间曲面的方程
F ( x , y , z ) = 0 z = f ( x , y ) F(x,y,z)=0\quad z=f(x,y)
F ( x , y , z ) = 0 z = f ( x , y )
空间曲线的方程:参数方程,一般方程。
{ x = x ( t ) y = y ( t ) z = z ( t ) { y = y ( x ) z = z ( x ) { F ( x , y , z ) = 0 G ( x , y , z ) = 0 \left\{ \begin{matrix}x=x(t)\\y=y(t)\\z=z(t)\end{matrix}\right. \quad \left\{ \begin{matrix}y=y(x)\\z=z(x)\end{matrix}\right.\quad \left\{ \begin{matrix}F(x,y,z)=0\\G(x,y,z)=0\end{matrix}\right.
⎩ ⎨ ⎧ x = x ( t ) y = y ( t ) z = z ( t ) { y = y ( x ) z = z ( x ) { F ( x , y , z ) = 0 G ( x , y , z ) = 0
柱面、旋转曲面的定义与计算。
平面、平面的点法式方程:
( P − P 0 ) ⋅ n = 0 (\boldsymbol P-\boldsymbol P_0)\cdot \boldsymbol n=0
( P − P 0 ) ⋅ n = 0
直线、直线的点向式方程:
x − x 0 A = y − y 0 B = z − z 0 C \frac{x-x_0}{A}=\frac{y-y_0}{B}=\frac{z-z_0}{C}
A x − x 0 = B y − y 0 = C z − z 0
设 t = t 0 t=t_0 t = t 0 M 0 ( x 0 , y 0 , z 0 ) M_0(x_0,y_0,z_0) M 0 ( x 0 , y 0 , z 0 ) x 0 = x ( t 0 ) x_0=x(t_0) x 0 = x ( t 0 ) y 0 = y ( t 0 ) y_0=y(t_0) y 0 = y ( t 0 ) z 0 = z ( t 0 ) z_0=z(t_0) z 0 = z ( t 0 )
观察两点 t = t 0 t=t_0 t = t 0 t = t 0 + Δ t t=t_0+\Delta t t = t 0 + Δ t Δ t → 0 \Delta t \to0 Δ t → 0
空间曲线的切线方程 :
x − x 0 x ′ ( t 0 ) = y − y 0 y ′ ( t 0 ) = z − z 0 z ′ ( t 0 ) \boxed{\frac{x-x_0}{x'(t_0)}=\frac{y-y_0}{y'(t_0)}=\frac{z-z_0}{z'(t_0)}}
x ′ ( t 0 ) x − x 0 = y ′ ( t 0 ) y − y 0 = z ′ ( t 0 ) z − z 0
空间曲线的法平面方程 :
x ′ ( t 0 ) ( x − x 0 ) + y ′ ( t 0 ) ( y − y 0 ) + z ′ ( t 0 ) ( z − z 0 ) = 0 x'(t_0)(x-x_0)+y'(t_0)(y-y_0)+z'(t_0)(z-z_0)=0
x ′ ( t 0 ) ( x − x 0 ) + y ′ ( t 0 ) ( y − y 0 ) + z ′ ( t 0 ) ( z − z 0 ) = 0
若参数方程为 y = y ( x ) , z = z ( x ) y=y(x),z=z(x) y = y ( x ) , z = z ( x )
空间曲线的切线方程 :
x − x 0 1 = y − y 0 y ′ ( x 0 ) = z − z 0 z ′ ( x 0 ) \boxed{\frac{x-x_0}{1}=\frac{y-y_0}{y'(x_0)}=\frac{z-z_0}{z'(x_0)}}
1 x − x 0 = y ′ ( x 0 ) y − y 0 = z ′ ( x 0 ) z − z 0
曲线在 M 0 M_0 M 0 法平面方程 为:
( x − x 0 ) + y ′ ( x 0 ) ( y − y 0 ) + z ′ ( x 0 ) ( z − z 0 ) = 0 (x-x_0)+y'(x_0)(y-y_0)+z'(x_0)(z-z_0)=0
( x − x 0 ) + y ′ ( x 0 ) ( y − y 0 ) + z ′ ( x 0 ) ( z − z 0 ) = 0
若由平面 F ( x , y , z ) = 0 F(x,y,z)=0 F ( x , y , z ) = 0 G ( x , y , z ) = 0 G(x,y,z)=0 G ( x , y , z ) = 0 y ′ ( x ) , z ′ ( x ) y'(x),z'(x) y ′ ( x ) , z ′ ( x )
则切向量
S ⃗ = { ∣ F y F z G y G z ∣ , ∣ F z F x G z G x ∣ , ∣ F x F y G x G y ∣ } \vec S=\left\{\begin{vmatrix}F_y & F_z\\G_y & G_z\end{vmatrix},\begin{vmatrix}F_z & F_x\\G_z & G_x\end{vmatrix},\begin{vmatrix}F_x & F_y\\G_x & G_y\end{vmatrix}\right\}
S = { ∣ ∣ ∣ ∣ F y G y F z G z ∣ ∣ ∣ ∣ , ∣ ∣ ∣ ∣ F z G z F x G x ∣ ∣ ∣ ∣ , ∣ ∣ ∣ ∣ F x G x F y G y ∣ ∣ ∣ ∣ }
为了计算更加简便,我们还可以使用
n ⃗ 1 = ( F x , F y , F z ) n ⃗ 2 = ( G x , G y , G z ) S ⃗ = n ⃗ 1 × n ⃗ 2 \vec n_1=(F_x,F_y,F_z) \quad \vec {n}_2 =(G_x,G_y,G_z)\\
\vec S = \vec n_1 \times \vec n_2
n 1 = ( F x , F y , F z ) n 2 = ( G x , G y , G z ) S = n 1 × n 2
几何意义,满足
{ F x d x + F y d y + F z d z = 0 G x d x + G y d y + G z d z = 0 \left\{
\begin{aligned}
&F_x \mathrm d x+F_y \mathrm d y+F_z \mathrm d z=0\\
&G_x \mathrm d x+G_y \mathrm d y+G_z \mathrm d z=0
\end{aligned}
\right.
{ F x d x + F y d y + F z d z = 0 G x d x + G y d y + G z d z = 0
因此,( d x , d y , d z ) (\mathrm d x,\mathrm d y,\mathrm d z) ( d x , d y , d z ) ( F x , F y , F z ) (F_x,F_y,F_z) ( F x , F y , F z ) ( G x , G y , G z ) (G_x,G_y,G_z) ( G x , G y , G z )
对于隐函数 F ( x , y , z ) = 0 F(x,y,z)=0 F ( x , y , z ) = 0
F x ( x 0 , y 0 , z 0 ) x ′ ( t 0 ) + F y ( x 0 , y 0 , z 0 ) y ′ ( t 0 ) + F z ( x 0 , y 0 , z 0 ) z ′ ( t 0 ) = 0 F_x(x_0,y_0,z_0) x'(t_0)+F_y(x_0,y_0,z_0)y'(t_0)+F_z(x_0,y_0,z_0)z'(t_0)=0
F x ( x 0 , y 0 , z 0 ) x ′ ( t 0 ) + F y ( x 0 , y 0 , z 0 ) y ′ ( t 0 ) + F z ( x 0 , y 0 , z 0 ) z ′ ( t 0 ) = 0
n ⃗ = { F x , F y , F z } \vec n=\{F_x,F_y,F_z\}
n = { F x , F y , F z }
切平面方程:
n ⃗ ⋅ ( P − P 0 ) = 0 \vec n \cdot (P-P_0)=0
n ⋅ ( P − P 0 ) = 0
对于 z = f ( x , y ) z=f(x,y) z = f ( x , y ) F = f ( x , y ) − z F=f(x,y)-z F = f ( x , y ) − z
设曲面 S S S F ( x , y , z ) = 0 F(x,y,z)=0 F ( x , y , z ) = 0 F x 2 + F y 2 + F z 2 ≠ 0 F_x^2+F_y^2+F_z^2 \not=0 F x 2 + F y 2 + F z 2 = 0 S S S
设最近点是 ( x 0 , y 0 , z 0 ) (x_0,y_0,z_0) ( x 0 , y 0 , z 0 )
x − x 0 F x = y − y 0 F y = z − z 0 F z \frac{x-x_0}{F_x} = \frac{y-y_0}{F_y}=\frac{z-z_0}{F_z}
F x x − x 0 = F y y − y 0 = F z z − z 0
坐标原点相当于证明
x 0 F x = y 0 F y = z 0 F z \frac{x_0}{F_x}=\frac{y_0}{F_y}=\frac{z_0}{F_z}
F x x 0 = F y y 0 = F z z 0
而设函数 r ( x , y , z ) = x 2 + y 2 + z 2 ( x , y ) r(x,y,z)=x^2+y^2+z^2(x,y) r ( x , y , z ) = x 2 + y 2 + z 2 ( x , y ) x , y x,y x , y
x 0 + z x z 0 = 0 y 0 + z y z 0 = 0 x_0+z_xz_0=0 \quad y_0+z_y z_0=0
x 0 + z x z 0 = 0 y 0 + z y z 0 = 0
代入 z x = − F x F z , z y = − F y F z z_x=-\frac{F_x}{F_z},z_y=-\frac{F_y}{F_z} z x = − F z F x , z y = − F z F y
设 S S S M 0 ( x 0 , y 0 , z 0 ) M_0(x_0,y_0,z_0) M 0 ( x 0 , y 0 , z 0 ) g ( x , y , z ) = x 2 + y 2 + z 2 = c g(x,y,z)=x^2+y^2+z^2=c g ( x , y , z ) = x 2 + y 2 + z 2 = c S S S M 0 M_0 M 0 x 2 + y 2 + z 2 = c x^2+y^2+z^2=c x 2 + y 2 + z 2 = c
故 S S S M 0 ( x 0 , y 0 , z 0 ) M_0(x_0,y_0,z_0) M 0 ( x 0 , y 0 , z 0 )
回顾一元函数的 n n n
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + ⋯ + f ( n ) ( x 0 ) n ! ( x − x 0 ) n + R n f(x)=f\left(x_0\right)+f^{\prime}\left(x_0\right)\left(x-x_0\right)+\frac{f^{\prime \prime}\left(x_0\right)}{2 !}\left(x-x_0\right)^2+\cdots+\frac{f^{(n)}\left(x_0\right)}{n !}\left(x-x_0\right)^n+R_n
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + 2 ! f ′ ′ ( x 0 ) ( x − x 0 ) 2 + ⋯ + n ! f ( n ) ( x 0 ) ( x − x 0 ) n + R n
(1)如果函数 f ( x ) f(x) f ( x ) x 0 x_0 x 0 n + 1 n+1 n + 1 R n = f ( n + 1 ) ( ξ ) ( n + 1 ) ! ( x − x 0 ) n + 1 R_n=\frac{f^{(n+1)}(\xi)}{(n+1) !}\left(x-x_0\right)^{n+1} R n = ( n + 1 ) ! f ( n + 1 ) ( ξ ) ( x − x 0 ) n + 1 ξ \xi ξ x , x 0 x, x_0 x , x 0 f ( x ) f(x) f ( x ) x 0 x_0 x 0 n n n R n = o ( ( x − x 0 ) n ) R_n=o\left(\left(x-x_0\right)^n\right) R n = o ( ( x − x 0 ) n ) o ( α ) o(\alpha) o ( α ) α \alpha α
函数 f ( x ) f(x) f ( x ) x 0 x_0 x 0
f ( x 0 + Δ x ) = f ( x 0 ) + f ′ ( x 0 ) Δ x + R 1 f\left(x_0+\Delta x\right)=f\left(x_0\right)+f^{\prime}\left(x_0\right) \Delta x+R_1
f ( x 0 + Δ x ) = f ( x 0 ) + f ′ ( x 0 ) Δ x + R 1
其中余项 R 1 = f ′ ′ [ x 0 + θ ⋅ Δ x ] 2 ! ( Δ x ) 2 , ( 0 < θ < 1 ) R_1=\frac{f^{\prime \prime}\left[x_0+\theta \cdot \Delta x\right]}{2 !}(\Delta x)^2,(0<\theta<1) R 1 = 2 ! f ′ ′ [ x 0 + θ ⋅ Δ x ] ( Δ x ) 2 , ( 0 < θ < 1 ) R 1 = o ( Δ x ) R_1=o(\Delta x) R 1 = o ( Δ x ) f ( x , y ) f(x, y) f ( x , y ) M 0 ( x 0 , y 0 ) M_0\left(x_0, y_0\right) M 0 ( x 0 , y 0 )
f ( x 0 + Δ x , y 0 + Δ y ) = f ( x 0 , y 0 ) + f x ( x 0 , y 0 ) Δ x + f y ( x 0 , y 0 ) Δ y + R 1 f\left(x_0+\Delta x, y_0+\Delta y\right)=f\left(x_0, y_0\right)+f_x\left(x_0, y_0\right) \Delta x+f_y\left(x_0, y_0\right) \Delta y+R_1
f ( x 0 + Δ x , y 0 + Δ y ) = f ( x 0 , y 0 ) + f x ( x 0 , y 0 ) Δ x + f y ( x 0 , y 0 ) Δ y + R 1
余项 R 1 = ? R_1=? R 1 = ?
设函数 f ( x , y ) f(x, y) f ( x , y ) M 0 ( x 0 , y 0 ) M_0\left(x_0, y_0\right) M 0 ( x 0 , y 0 )
f ( x 0 + Δ x , y 0 + Δ y ) = f ( x 0 , y 0 ) + f x ( x 0 , y 0 ) Δ x + f y ( x 0 , y 0 ) Δ y + R 1 f\left(x_0+\Delta x, y_0+\Delta y\right)=f\left(x_0, y_0\right)+f_x\left(x_0, y_0\right) \Delta x+f_y\left(x_0, y_0\right) \Delta y+R_1
f ( x 0 + Δ x , y 0 + Δ y ) = f ( x 0 , y 0 ) + f x ( x 0 , y 0 ) Δ x + f y ( x 0 , y 0 ) Δ y + R 1
其中余项
R 1 = 1 2 [ ( Δ x ) 2 f x x + 2 Δ x Δ y f x y + ( Δ y ) 2 f y y ] ∣ ( x 0 + θ Δ x , y 0 + θ Δ y ) , ( 0 < θ < 1 ) , R_1=\left.\frac{1}{2}\left[(\Delta x)^2 f_{x x}+2 \Delta x \Delta y f_{x y}+(\Delta y)^2 f_{y y}\right]\right|_{\left(x_0+\theta \Delta x, y_0+\theta \Delta y\right)},(0<\theta<1),
R 1 = 2 1 [ ( Δ x ) 2 f x x + 2 Δ x Δ y f x y + ( Δ y ) 2 f y y ] ∣ ∣ ∣ ∣ ( x 0 + θ Δ x , y 0 + θ Δ y ) , ( 0 < θ < 1 ) ,
或 R 1 = o ( ρ ) , ρ = ( Δ x ) 2 + ( Δ y ) 2 R_1=o(\rho), \rho=\sqrt{(\Delta x)^2+(\Delta y)^2} R 1 = o ( ρ ) , ρ = ( Δ x ) 2 + ( Δ y ) 2
我们先引入运算符号或微分算子
D = Δ x ∂ ∂ x + Δ y ∂ ∂ y , D=\Delta x \frac{\partial}{\partial x}+\Delta y \frac{\partial}{\partial y} \text {, }
D = Δ x ∂ x ∂ + Δ y ∂ y ∂ ,
则 D f = ( Δ x ∂ ∂ x + Δ y ∂ ∂ y ) f = Δ x ∂ f ∂ x + Δ y ∂ f ∂ y D f=\left(\Delta x \frac{\partial}{\partial x}+\Delta y \frac{\partial}{\partial y}\right) f=\Delta x \frac{\partial f}{\partial x}+\Delta y \frac{\partial f}{\partial y} D f = ( Δ x ∂ x ∂ + Δ y ∂ y ∂ ) f = Δ x ∂ x ∂ f + Δ y ∂ y ∂ f
D 2 f = ( Δ x ∂ ∂ x + Δ y ∂ ∂ y ) 2 f = ( Δ x ) 2 ∂ 2 f ∂ x 2 + 2 Δ x Δ y ∂ 2 f ∂ x ∂ y + ( Δ y ) 2 ∂ 2 f ∂ y 2 , D^2 f=\left(\Delta x \frac{\partial}{\partial x}+\Delta y \frac{\partial}{\partial y}\right)^2 f=(\Delta x)^2 \frac{\partial^2 f}{\partial x^2}+2 \Delta x \Delta y \frac{\partial^2 f}{\partial x \partial y}+(\Delta y)^2 \frac{\partial^2 f}{\partial y^2},
D 2 f = ( Δ x ∂ x ∂ + Δ y ∂ y ∂ ) 2 f = ( Δ x ) 2 ∂ x 2 ∂ 2 f + 2 Δ x Δ y ∂ x ∂ y ∂ 2 f + ( Δ y ) 2 ∂ y 2 ∂ 2 f ,
二元函数的 n n n
D n f = ( Δ x ∂ ∂ x + Δ y ∂ ∂ y ) n f = = ( Δ x ) n ∂ n f ∂ x n + C n 1 ( Δ x ) n − 1 Δ y ∂ n f ∂ x n − 1 ∂ y + ⋯ + ( Δ y ) n ∂ n f ∂ y n \begin{aligned}
D^n f & =\left(\Delta x \frac{\partial}{\partial x}+\Delta y \frac{\partial}{\partial y}\right)^n f= \\
& =(\Delta x)^n \frac{\partial^n f}{\partial x^n}+C_n^1(\Delta x)^{n-1} \Delta y \frac{\partial^n f}{\partial x^{n-1} \partial y}+\cdots+(\Delta y)^n \frac{\partial^n f}{\partial y^n}
\end{aligned}
D n f = ( Δ x ∂ x ∂ + Δ y ∂ y ∂ ) n f = = ( Δ x ) n ∂ x n ∂ n f + C n 1 ( Δ x ) n − 1 Δ y ∂ x n − 1 ∂ y ∂ n f + ⋯ + ( Δ y ) n ∂ y n ∂ n f
其中通项为 C n k ( Δ x ) n − k ( Δ y ) k ∂ n f ∂ x n − k ∂ y k C_n^k(\Delta x)^{n-k}(\Delta y)^k \frac{\partial^n f}{\partial x^{n-k} \partial y^k} C n k ( Δ x ) n − k ( Δ y ) k ∂ x n − k ∂ y k ∂ n f
设函数 f ( x , y ) f(x,y) f ( x , y ) M 0 ( x 0 , y 0 ) M_0(x_0,y_0) M 0 ( x 0 , y 0 ) U ( M 0 ) U(M_0) U ( M 0 ) 连续的二阶偏导数 ,且点 M 0 M_0 M 0 f ( x , y ) f(x,y) f ( x , y ) 驻点 (f x ( x 0 , y 0 ) = f y ( x 0 , y 0 ) = 0 f_x(x_0,y_0)=f_y(x_0,y_0)=0 f x ( x 0 , y 0 ) = f y ( x 0 , y 0 ) = 0
f x x ( x 0 , y 0 ) = A , f x y ( x 0 , y 0 ) = B , f y y ( x 0 , y 0 ) = C f_{xx}(x_0,y_0)=A,f_{xy}(x_0,y_0)=B,f_{yy}(x_0,y_0)=C
f x x ( x 0 , y 0 ) = A , f x y ( x 0 , y 0 ) = B , f y y ( x 0 , y 0 ) = C
则
当 B 2 − A C < 0 B^2-AC<0 B 2 − A C < 0 f ( x , y ) f(x,y) f ( x , y ) M 0 M_0 M 0
A > 0 A>0 A > 0 f ( x 0 , y 0 ) f(x_0,y_0) f ( x 0 , y 0 ) A < 0 A<0 A < 0 f ( x 0 , y 0 ) f(x_0,y_0) f ( x 0 , y 0 )
当 B 2 − A C > 0 B^2-AC>0 B 2 − A C > 0 f ( x 0 , y 0 ) f(x_0,y_0) f ( x 0 , y 0 ) f ( x , y ) f(x,y) f ( x , y )
证明:
R 1 = 1 2 ( ( Δ x ) 2 f x x + 2 Δ x Δ y f x y + ( Δ y ) 2 f y y ) ∣ ( x 0 + θ Δ x , y 0 + θ Δ y ) R_1= \frac{1}{2} ((\Delta x)^2 f_{xx}+2\Delta x\Delta y f_{xy} + (\Delta y)^2 f_{yy})|_{(x_0+\theta \Delta x,y_0+\theta\Delta y)}
R 1 = 2 1 ( ( Δ x ) 2 f x x + 2 Δ x Δ y f x y + ( Δ y ) 2 f y y ) ∣ ( x 0 + θ Δ x , y 0 + θ Δ y )
就要分析 R 1 R_1 R 1
当 B 2 − A C < 0 B^2-AC<0 B 2 − A C < 0 A , C A,C A , C A > 0 A>0 A > 0 R 1 > 0 R_1 >0 R 1 > 0 A < 0 A<0 A < 0 R 1 < 0 R_1 <0 R 1 < 0
当 B 2 − A C > 0 B^2-AC>0 B 2 − A C > 0 R 1 R_1 R 1
当 B 2 − A C = 0 B^2-AC=0 B 2 − A C = 0 z = ∣ x y ∣ , z = x y z=|xy|,z=xy z = ∣ x y ∣ , z = x y
在这里使用极坐标代换,第一个得到
z = r 2 ∣ sin θ cos θ ∣ z=r^2 |\sin\theta\cos\theta\,|
z = r 2 ∣ sin θ cos θ ∣
显然是极小值点。
第二个得到
z = r 2 sin θ cos θ z=r^2 \sin\theta\cos\theta
z = r 2 sin θ cos θ
显然可正可负。
主要利用驻点的条件。
设常数 R > 0 , f ( x , y ) R>0, f(x, y) R > 0 , f ( x , y ) D = { ( x , y ) ∣ x 2 + y 2 ≤ R 2 } D=\left\{(x, y) \mid x^2+y^2 \leq R^2\right\} D = { ( x , y ) ∣ x 2 + y 2 ≤ R 2 } f ( 0 , 0 ) = 0 , ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 = 0 , ∂ 2 f ∂ x ∂ y ≠ 0 f(0,0)=0, \frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2}=0, \frac{\partial^2 f}{\partial x \partial y} \neq 0 f ( 0 , 0 ) = 0 , ∂ x 2 ∂ 2 f + ∂ y 2 ∂ 2 f = 0 , ∂ x ∂ y ∂ 2 f = 0 ∀ r : 0 < r ≤ R \forall r: 0<r \leq R ∀ r : 0 < r ≤ R C r = { ( x , y ) ∣ x 2 + y 2 = r 2 } C_r=\left\{(x, y) \mid x^2+y^2=r^2\right\} C r = { ( x , y ) ∣ x 2 + y 2 = r 2 } ( x 0 , y 0 ) \left(x_0, y_0\right) ( x 0 , y 0 ) f ( x 0 , y 0 ) = 0 f\left(x_0, y_0\right)=0 f ( x 0 , y 0 ) = 0 ∂ 2 f ∂ x 2 ⋅ ∂ 2 f ∂ y 2 − ( ∂ 2 f ∂ x ∂ y ) 2 < 0 \frac{\partial^2 f}{\partial x^2} \cdot \frac{\partial^2 f}{\partial y^2}-\left(\frac{\partial^2 f}{\partial x \partial y}\right)^2<0 ∂ x 2 ∂ 2 f ⋅ ∂ y 2 ∂ 2 f − ( ∂ x ∂ y ∂ 2 f ) 2 < 0 f ( x , y ) f(x, y) f ( x , y ) D r = { ( x , y ) ∣ x 2 + y 2 ≤ r 2 } D_r=\left\{(x, y) \mid x^2+y^2 \leq r^2\right\} D r = { ( x , y ) ∣ x 2 + y 2 ≤ r 2 } f ( x , y ) f(x, y) f ( x , y ) D r D_r D r C r C_r C r f ( 0 , 0 ) = 0 f(0,0)=0 f ( 0 , 0 ) = 0 M = max D r f ( x , y ) > 0 , m = min D r f ( x , y ) < 0 M=\max _{D_r} f(x, y)>0, m=\min _{D_r} f(x, y)<0 M = max D r f ( x , y ) > 0 , m = min D r f ( x , y ) < 0 f ( x , y ) f(x, y) f ( x , y ) C r C_r C r M , m M, m M , m f ∣ C r ( x , y ) \left.f\right|_{C_r}(x, y) f ∣ C r ( x , y ) C r C_r C r \quad
事实上, f ( x , y ) f(x, y) f ( x , y ) C r C_r C r
注: f ( x , y ) = x y f(x, y)=x y f ( x , y ) = x y z = x y z=x y z = x y f ( x , y ) = x y f(x, y)=x y f ( x , y ) = x y C r C_r C r ( 0 , ± r ) , ( ± r , 0 ) (0, \pm r),( \pm r, 0) ( 0 , ± r ) , ( ± r , 0 )
分析极值,还可以使用极坐标代换,极坐标代换在原式齐次的情况下好用
例如,分析 f ( x , y ) = 4 x y + x 2 + y 2 f(x,y)=4xy+x^2+y^2 f ( x , y ) = 4 x y + x 2 + y 2 ( 0 , 0 ) (0,0) ( 0 , 0 )
f ( r cos θ , r sin θ ) = r 2 ( 1 + 2 sin 2 θ ) f(r\cos\theta,r\sin\theta)=r^2(1+2\sin2\theta)
f ( r cos θ , r sin θ ) = r 2 ( 1 + 2 sin 2 θ )
后一项可正可负,因此不取极值。
在原式显然非齐次的情况下,需要通过特殊代换使得原式齐次,为什么我们希望齐次式,是因为可以提取 ρ k f ( θ ) \rho^k f(\theta) ρ k f ( θ )
分析 f ( x , y ) = x 4 − 3 x 2 y + 2 y 2 f(x,y)=x^4-3x^2y+2y^2 f ( x , y ) = x 4 − 3 x 2 y + 2 y 2 ( 0 , 0 ) (0,0) ( 0 , 0 )
f ( x , k x 2 ) = x 4 ( 2 k − 1 ) ( k − 1 ) f(x,kx^2)=x^4(2k-1)(k-1)
f ( x , k x 2 ) = x 4 ( 2 k − 1 ) ( k − 1 )
显然可正可负,因此不是极小值点。
如果 F F F F F F
H ( F ) ( x ) = [ ∂ 2 F ∂ x 1 2 ∂ F ∂ x 1 ∂ x 2 ⋯ ∂ F ∂ x 1 ∂ x n ∂ 2 F ∂ x 2 ∂ x 1 ∂ F ∂ x 2 2 ⋯ ∂ F ∂ x 2 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ 2 F ∂ x n ∂ x 1 ∂ F ∂ x n ∂ x 2 ⋯ ∂ F ∂ x n 2 ] H(F)(\boldsymbol{x}) =
\left [
\begin{matrix}
\frac {\partial^2F} {\partial x_1^2} & \frac {\partial^F} {\partial x_1 \partial x_2} & \cdots & \frac {\partial^F} {\partial x_1 \partial x_n} \\
\frac {\partial^2F} {\partial x_2 \partial x_1} & \frac {\partial^F} {\partial x_2^2} & \cdots & \frac {\partial^F} {\partial x_2 \partial x_n} \\
\vdots & \vdots & \ddots & \vdots \\
\frac {\partial^2F} {\partial x_n \partial x_1} & \frac {\partial^F} {\partial x_n \partial x_2} & \cdots & \frac {\partial^F} {\partial x_n^2}
\end{matrix}
\right] \\
H ( F ) ( x ) = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ∂ x 1 2 ∂ 2 F ∂ x 2 ∂ x 1 ∂ 2 F ⋮ ∂ x n ∂ x 1 ∂ 2 F ∂ x 1 ∂ x 2 ∂ F ∂ x 2 2 ∂ F ⋮ ∂ x n ∂ x 2 ∂ F ⋯ ⋯ ⋱ ⋯ ∂ x 1 ∂ x n ∂ F ∂ x 2 ∂ x n ∂ F ⋮ ∂ x n 2 ∂ F ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
利用迭代法求解函数零点:
x n + 1 = x n − [ H ( F ) ( x n ) ] − 1 ∇ F ( x n ) \boldsymbol x_{n+1}=\boldsymbol x_n -[H(F)(\boldsymbol x_n)]^{-1}\nabla F(\boldsymbol x_n)
x n + 1 = x n − [ H ( F ) ( x n ) ] − 1 ∇ F ( x n )
当 Hessian 矩阵正定的时候,对于任意的方向向量 v T v^T v T v T H v > 0 v^T Hv >0 v T H v > 0 0 0 0
f ( x + ε v ) ≈ f ( x ( 0 ) ) + 1 2 ε 2 v T H v > f ( x ( 0 ) ) f(\boldsymbol x +\varepsilon v) \approx f(\boldsymbol x^{(0)}) + \frac{1}{2} \varepsilon ^2 v^T Hv>f(x^{(0)})
f ( x + ε v ) ≈ f ( x ( 0 ) ) + 2 1 ε 2 v T H v > f ( x ( 0 ) )
minimize f ( x , y ) , s . t . g ( x , y ) = 0 \operatorname{minimize} f(x,y) ,s.t. g(x,y)=0 m i n i m i z e f ( x , y ) , s . t . g ( x , y ) = 0
f x ⋅ 1 + f y ⋅ ∂ x ∂ y = f x − f y ⋅ g y g x = 0 f_x \cdot 1 + f_y \cdot \frac{\partial x}{\partial y}=f_x - f_y \cdot \frac{g_y}{g_x}=0
f x ⋅ 1 + f y ⋅ ∂ y ∂ x = f x − f y ⋅ g x g y = 0
记
λ = f x g x = f y g y \lambda=\frac{f_x}{g_x}=\frac{f_y}{g_y}
λ = g x f x = g y f y
所以
{ f x − λ g x = 0 f y − λ g y = 0 g ( x , y ) = 0 \left\{ \begin{matrix}f_x-\lambda g_x =0\\f_y-\lambda g_y=0\\g(x,y)=0\end{matrix}\right.
⎩ ⎨ ⎧ f x − λ g x = 0 f y − λ g y = 0 g ( x , y ) = 0
minimize f ( x , y , z ) , s . t . g ( x , y , z ) = 0 \operatorname{minimize} f(x,y,z) ,s.t. g(x,y,z)=0 m i n i m i z e f ( x , y , z ) , s . t . g ( x , y , z ) = 0
一元函数 f ( x ) , x ∈ [ a , b ] f(x) ,x \in [a,b] f ( x ) , x ∈ [ a , b ]
求函数 f ( x , y ) = 2 x 2 + 6 x y + y 2 f(x,y)=2x^2+6xy+y^2 f ( x , y ) = 2 x 2 + 6 x y + y 2 x 2 + 2 y 2 ≤ 3 x^2+2y^2 \le 3 x 2 + 2 y 2 ≤ 3
内部:x 2 + 2 y 2 < 3 x^2+2y^2 <3 x 2 + 2 y 2 < 3
{ f x = 4 x + 6 y = 0 f y = 6 x + 2 y = 0 \left\{ \begin{matrix}f_x=4x+6y=0\\f_y=6x+2y=0\end{matrix}\right.
{ f x = 4 x + 6 y = 0 f y = 6 x + 2 y = 0
内部只有一个驻点。不用判断是极大值还是极小值。
边界:x 2 + 2 y 2 = 3 x^2+2y^2=3 x 2 + 2 y 2 = 3
L ( x , y , λ ) = f ( x , y ) + λ ( x 2 + 2 y 2 − 3 ) L(x,y,\lambda)=f(x,y)+\lambda(x^2+2y^2-3)
L ( x , y , λ ) = f ( x , y ) + λ ( x 2 + 2 y 2 − 3 )
若函数 z = f ( x , y ) z=f(x,y) z = f ( x , y ) f ( t x , t y ) = t k f ( x , y ) f(tx,ty)=t^kf(x,y) f ( t x , t y ) = t k f ( x , y ) k k k k k k f ( x , y ) f(x,y) f ( x , y ) z = x k F ( y / x ) z=x^k F(y/x) z = x k F ( y / x )
因为 z = f ( x , y ) = t − k f ( t x , t y ) z=f(x,y)=t^{-k}f(tx,ty) z = f ( x , y ) = t − k f ( t x , t y ) t = 1 / x t=1/x t = 1 / x
z = f ( x , y ) = x k f ( x 1 x , 1 x y ) = x k F ( y x ) z=f(x,y)=x^k f(x \frac{1}{x},\frac{1}{x}y)=x^kF\left(\frac{y}{x}\right)
z = f ( x , y ) = x k f ( x x 1 , x 1 y ) = x k F ( x y )
主要是掌握好几个关键的不等式。
这种题目可以看看分母趋近于 0 0 0
取 3 x + 2 y = 1 3x+2y=1 3 x + 2 y = 1
取 x + y = o ( x ) x+y=o(x) x + y = o ( x ) x + y = x 3 x+y=x^3 x + y = x 3
总结:分母 ≥ 0 \ge 0 ≥ 0
lim x → 0 , y → 0 ( x 2 + y 2 ) x 2 y 2 = exp ( lim x → 0 , y → 0 x 2 y 2 ln ( x 2 + y 2 ) ) = exp ( lim x → 0 , y → 0 x 2 y 2 x 2 + y 2 ( x 2 + y 2 ) ln ( x 2 + y 2 ) ) \lim_{x\to0,y\to0}(x^2+y^2)^{x^2y^2}=\exp(\lim_{x\to0,y\to0} x^2y^2\ln(x^2+y^2))\\=\exp\left(\lim_{x\to0,y\to0} \frac{x^2y^2}{x^2+y^2}(x^2+y^2)\ln(x^2+y^2)\right)
x → 0 , y → 0 lim ( x 2 + y 2 ) x 2 y 2 = exp ( x → 0 , y → 0 lim x 2 y 2 ln ( x 2 + y 2 ) ) = exp ( x → 0 , y → 0 lim x 2 + y 2 x 2 y 2 ( x 2 + y 2 ) ln ( x 2 + y 2 ) )
其中由于 ∣ x 2 y 2 x 2 + y 2 ∣ ⩽ ∣ x 2 y 2 2 x y ∣ = 1 2 ∣ x y ∣ → 0 \left|\frac{x^2 y^2}{x^2+y^2}\right| \leqslant\left|\frac{x^2 y^2}{2 x y}\right|=\frac{1}{2}|x y| \rightarrow 0 ∣ ∣ ∣ x 2 + y 2 x 2 y 2 ∣ ∣ ∣ ⩽ ∣ ∣ ∣ 2 x y x 2 y 2 ∣ ∣ ∣ = 2 1 ∣ x y ∣ → 0 ( x , y ) → ( 0 , 0 ) (x, y) \rightarrow(0,0) ( x , y ) → ( 0 , 0 )
\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}}\left(x^2+y^2\right) \ln \left(x^2+y^2\right) \text { 中令 } x^2+y^2=t \text {, }
由于
lim t → 0 t ln t = lim t → 0 ln t 1 t = lim t → 0 1 t − 1 t 2 = 0 , \lim _{t \rightarrow 0} t \ln t=\lim _{t \rightarrow 0} \frac{\ln t}{\frac{1}{t}}=\lim _{t \rightarrow 0} \frac{\frac{1}{t}}{-\frac{1}{t^2}}=0,
t → 0 lim t ln t = t → 0 lim t 1 ln t = t → 0 lim − t 2 1 t 1 = 0 ,
故
\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{x^2 y^2}{x^2+y^2}\left(x^2+y^2\right) \ln \left(x^2+y^2\right)=0,
\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}}\left(x^2+y^2\right)^{x^2 y^2}=\mathrm{e}^0=1 .
只需证明
lim x → 0 , y → 0 x y x 2 − y 2 x 2 + y 2 = 0 \lim_{x\to0,y\to0}xy\frac{x^2-y^2}{x^2+y^2}=0
x → 0 , y → 0 lim x y x 2 + y 2 x 2 − y 2 = 0
而
0 < ∣ x y x 2 − y 2 x 2 + y 2 ∣ = ∣ x y ∣ ∣ x 2 − y 2 x 2 + y 2 ∣ ≤ ∣ x y ∣ 0<\left|xy\frac{x^2-y^2}{x^2+y^2}\right|=|xy|\left|\frac{x^2-y^2}{x^2+y^2}\right|\le |xy|
0 < ∣ ∣ ∣ ∣ x y x 2 + y 2 x 2 − y 2 ∣ ∣ ∣ ∣ = ∣ x y ∣ ∣ ∣ ∣ ∣ x 2 + y 2 x 2 − y 2 ∣ ∣ ∣ ∣ ≤ ∣ x y ∣
注意:f x ( x , y ) f_x(x,y) f x ( x , y ) f x ( x , 1 ) f_x(x,1) f x ( x , 1 ) y = 1 y=1 y = 1 f x ( x , y ) f_x(x,y) f x ( x , y ) f ( x , 1 ) f(x,1) f ( x , 1 )
f x ( 0 , 0 ) = lim Δ x → 0 ( f ( Δ x , 0 ) − f ( 0 , 0 ) ) / Δ x = lim Δ x → 0 ∣ Δ x ∣ g ( 0 , 0 ) / Δ x f_x(0,0)=\lim_{\Delta x \to 0} (f(\Delta x,0)-f(0,0))/\Delta x=\lim_{\Delta x \to 0}|\Delta x| g(0,0)/\Delta x
f x ( 0 , 0 ) = Δ x → 0 lim ( f ( Δ x , 0 ) − f ( 0 , 0 ) ) / Δ x = Δ x → 0 lim ∣ Δ x ∣ g ( 0 , 0 ) / Δ x
需要 g ( 0 , 0 ) = 0 g(0,0)=0 g ( 0 , 0 ) = 0
求 f x y ( 0 , 0 ) f_{xy}(0,0) f x y ( 0 , 0 )
求出 f x y ( x , y ) f_{xy}(x,y) f x y ( x , y ) x , y x,y x , y
注意到最后对 y y y y y y f x ( x , y ) f_{x}(x,y) f x ( x , y ) x = 0 x=0 x = 0 f x ( 0 , y ) f_x(0,y) f x ( 0 , y ) y y y
注意
f y ( x , 0 ) = lim Δ y → 0 f ( x , Δ y ) − f ( x , 0 ) Δ y = lim Δ y → 0 f ( x , Δ y ) − 1 Δ y = x f_y(x,0)=\lim_{\Delta y \to 0}\frac{f(x,\Delta y)-f(x,0)}{\Delta y}=\lim_{\Delta y \to 0} \frac{f(x,\Delta y)-1}{\Delta y}=x
f y ( x , 0 ) = Δ y → 0 lim Δ y f ( x , Δ y ) − f ( x , 0 ) = Δ y → 0 lim Δ y f ( x , Δ y ) − 1 = x
因此,f ( x , y ) = 1 + x y + o ( y ) f(x,y)=1+xy+o(y) f ( x , y ) = 1 + x y + o ( y )
而 f y y = 2 f_{yy}=2 f y y = 2 f y = x + o ( y ) ′ , f y y = o ( y ) ′ ′ f_y=x+o(y)',f_{yy}=o(y)'' f y = x + o ( y ) ′ , f y y = o ( y ) ′ ′ o ( y ) = y 2 o(y)=y^2 o ( y ) = y 2
因此
f ( x , y ) = y 2 + x y + 1 f(x,y)=y^2+xy+1
f ( x , y ) = y 2 + x y + 1
∂ F ∂ x = ∫ 0 y x f ( x ) g ( 1 x ) d t = y x f ( x ) g ( 1 x ) \frac{\partial F}{\partial x}=\int_0^{yx} f(x)g\left(\frac{1}{x}\right)\mathrm d t=yxf(x)g\left(\frac{1}{x}\right)
∂ x ∂ F = ∫ 0 y x f ( x ) g ( x 1 ) d t = y x f ( x ) g ( x 1 )
∂ 2 F ∂ x ∂ y = x f ( x ) g ( 1 x ) \frac{\partial^2 F}{\partial x\partial y}=xf(x)g(\frac{1}{x})
∂ x ∂ y ∂ 2 F = x f ( x ) g ( x 1 )
注意符号的代换。
两种代换方式,第一种是 r ( x , y ) , θ ( x , y ) r(x,y),\theta(x,y) r ( x , y ) , θ ( x , y ) x ( r , θ ) , y ( r , θ ) x(r,\theta),y(r,\theta) x ( r , θ ) , y ( r , θ )
这里,我们选用第二种。
u r = u x x r + u y y r = v y cos θ − v x sin θ u_r=u_xx_r+u_yy_r=v_y\cos \theta-v_x\sin\theta
u r = u x x r + u y y r = v y cos θ − v x sin θ
v θ = v x x θ + v y y θ = v y r cos θ − v x r sin θ v_\theta=v_xx_\theta+v_yy_\theta=v_yr\cos \theta-v_x r \sin \theta
v θ = v x x θ + v y y θ = v y r cos θ − v x r sin θ
下面也是同理。
齐次函数可以表示为:
f ( x , y , z ) = x k F ( y x , z x ) f(x,y,z)=x^kF(\frac{y}{x},\frac{z}{x})
f ( x , y , z ) = x k F ( x y , x z )
因此,求导之后:
x ⋅ k x k − 1 F ( y x , z x ) − x k ( y x 2 F 1 + z x 2 F 2 ) + y x k 1 x F 1 + z x k 1 x F 2 = k x k F ( y x , z x ) x\cdot kx^{k-1}F(\frac{y}{x},\frac{z}{x})-x^k (\frac{y}{x^2}F_1+\frac{z}{x^2}F_2)+yx^{k}\frac{1}{x}F_1+zx^k
\frac{1}{x}F_2=kx^kF(\frac{y}{x},\frac{z}{x})
x ⋅ k x k − 1 F ( x y , x z ) − x k ( x 2 y F 1 + x 2 z F 2 ) + y x k x 1 F 1 + z x k x 1 F 2 = k x k F ( x y , x z )
法2:
令 u = x t , v = y t , w = z t u=xt,v=yt,w=zt u = x t , v = y t , w = z t
对关系式
f ( u , v , w ) = t k f ( x , y , z ) f(u,v,w)=t^k f(x,y,z)
f ( u , v , w ) = t k f ( x , y , z )
两边对 t t t
u t = u ξ ξ t + u η η t = u ξ + u η u_t=u_{\xi} \xi_t+u_{\eta}\eta_t=u_{\xi}+u_{\eta}
u t = u ξ ξ t + u η η t = u ξ + u η
∂ 2 u ∂ ξ ∂ η = 0 \frac{\partial^2 u}{\partial \xi\partial \eta}=0 ∂ ξ ∂ η ∂ 2 u = 0
u x ( x , 2 x ) u_x(x,2x) u x ( x , 2 x ) u ( x , y ) u(x,y) u ( x , y ) y = 2 x y=2x y = 2 x
∂ 2 u ∂ ξ ∂ η = 0 \frac{\partial^2 u}{\partial \xi\partial \eta}=0 ∂ ξ ∂ η ∂ 2 u = 0 ∂ u / ∂ ξ \partial u/\partial \xi ∂ u / ∂ ξ ξ \xi ξ
u = φ ( ξ ) + ψ ( η ) u=\varphi(\xi)+\psi(\eta)
u = φ ( ξ ) + ψ ( η )
隐函数的偏导数。
F ( x , y , z ) = x 2 + y 2 + z 2 − x f ( y x ) F(x,y,z)=x^2+y^2+z^2-xf(\frac{y}{x})
F ( x , y , z ) = x 2 + y 2 + z 2 − x f ( x y )
∂ z ∂ x = − F x F z = 2 x − y x f ′ ( y x ) + f ( y x ) 2 z \frac{\partial z}{\partial x}=-\frac{F_x}{F_z}=\frac{2x-\frac{y}{x}f'(\frac{y}{x})+f(\frac{y}{x})}{2z}
∂ x ∂ z = − F z F x = 2 z 2 x − x y f ′ ( x y ) + f ( x y )
{ F ( x , y , z ) = 0 G ( x , y , z ) = φ ( x + y ) + x − z = 0 \left\{
\begin{matrix}
F(x,y,z)=0\\
G(x,y,z)=\varphi(x+y)+x-z=0
\end{matrix}
\right.
{ F ( x , y , z ) = 0 G ( x , y , z ) = φ ( x + y ) + x − z = 0
得到
d y d x = − ∣ F x F z φ ′ + 1 − 1 ∣ ∣ F y F z φ ′ − 1 ∣ \frac{\mathrm d y}{\mathrm d x}=-\frac{\begin{vmatrix}F_x&F_z\\\varphi'+1&-1\end{vmatrix}}{\begin{vmatrix}F_y&F_z\\\varphi'&-1\end{vmatrix}}
d x d y = − ∣ ∣ ∣ ∣ F y φ ′ F z − 1 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ F x φ ′ + 1 F z − 1 ∣ ∣ ∣ ∣
确定多少个函数就需要多少个方程组。有点线性代数的思想在里面。
求全微分:
{ d x = d u + d v d y = d u − d v d z = u d v + v d u \left\{
\begin{matrix}
\mathrm d x=\mathrm du+\mathrm dv\\
\mathrm dy=\mathrm du-\mathrm dv\\
\mathrm dz=u\mathrm dv+v\mathrm du
\end{matrix}
\right.
⎩ ⎨ ⎧ d x = d u + d v d y = d u − d v d z = u d v + v d u
也可以:
注:对 x x x
{ d u = 2 x d x + 2 y d y d v = − 1 x 2 d x − 1 y 2 d y \left\{
\begin{matrix}
\mathrm d u=2x\mathrm d x+2y\mathrm d y\\
\mathrm d v=-\frac{1}{x^2}\mathrm d x-\frac{1}{y^2}\mathrm d y
\end{matrix}
\right.
{ d u = 2 x d x + 2 y d y d v = − x 2 1 d x − y 2 1 d y
{ d y = y 2 2 ( y 3 − x 3 ) ( d u + 2 x 3 d v ) d x = x 2 2 ( x 3 − y 3 ) ( d v + 2 y 3 d u ) \left\{
\begin{matrix}
\mathrm d y=\frac{y^2}{2(y^3-x^3)}(\mathrm d u+2x^3\mathrm d v)\\
\mathrm d x=\frac{x^2}{2(x^3-y^3)}(\mathrm d v+2y^3\mathrm d u)
\end{matrix}
\right.
{ d y = 2 ( y 3 − x 3 ) y 2 ( d u + 2 x 3 d v ) d x = 2 ( x 3 − y 3 ) x 2 ( d v + 2 y 3 d u )
在 w = ln z − ( x + y ) w=\ln z-(x+y) w = ln z − ( x + y ) x x x w = w ( u , v ) , u = u ( x , y ) , v = v ( x , y ) w=w(u,v),u=u(x,y),v=v(x,y) w = w ( u , v ) , u = u ( x , y ) , v = v ( x , y )
理清楚函数变量之间的关系。
2 x ∂ w ∂ u − 1 x 2 ∂ w ∂ v = 1 z ∂ z ∂ x − 1 2x \frac{\partial w}{\partial u}-\frac{1}{x^2}\frac{\partial w}{\partial v}=\frac{1}{z}\frac{\partial z}{\partial x}-1
2 x ∂ u ∂ w − x 2 1 ∂ v ∂ w = z 1 ∂ x ∂ z − 1
得到
∂ z ∂ x \frac{\partial z}{\partial x}
∂ x ∂ z
的表达式。
变换方程最难办的地方在于含有偏导数的地方。因此需要构造含有这个偏导数的式子。
注意抛物线的方向有两个。
矢径:位置矢量。
说明梯度 ( 2 x / a 2 , 2 y / b 2 , 2 z / c 2 ) (2x/a^2,2y/b^2,2z/c^2) ( 2 x / a 2 , 2 y / b 2 , 2 z / c 2 ) ( x , y , z ) / x 2 + y 2 + z 2 (x,y,z)/\sqrt{x^2+y^2+z^2} ( x , y , z ) / x 2 + y 2 + z 2
因此 ∣ a ∣ = ∣ b ∣ = ∣ c ∣ |a|=|b|=|c| ∣ a ∣ = ∣ b ∣ = ∣ c ∣
求曲面 a x 2 + b y 2 + c z 2 = 1 ax^2+by^2+cz^2=1 a x 2 + b y 2 + c z 2 = 1 ( x 0 , y 0 , z 0 ) (x_0,y_0,z_0) ( x 0 , y 0 , z 0 )
2 a x 0 ( x − x 0 ) + 2 b y 0 ( y − y 0 ) + 2 c z 0 ( z − z 0 ) = 0 2ax_0(x-x_0)+2by_0(y-y_0)+2cz_0(z-z_0)=0
2 a x 0 ( x − x 0 ) + 2 b y 0 ( y − y 0 ) + 2 c z 0 ( z − z 0 ) = 0
并且注意代入题目条件。
切平面:
a x x 0 + b y y 0 + c z z 0 = 1 axx_0+byy_0+czz_0=1
a x x 0 + b y y 0 + c z z 0 = 1
二阶泰勒公式的形式:
f ( x , y ) = f ( x 0 , y 0 ) + f x ( x 0 , y 0 ) ( x − x 0 ) + f y ( x 0 , y 0 ) ( y − y 0 ) + 1 2 ( f x x ( x 0 , y 0 ) ( x − x 0 ) 2 + 2 f x y ( x 0 , y 0 ) ( x − x 0 ) ( y − y 0 ) + f y y ( x 0 , y 0 ) ( y − y 0 ) 2 ) f(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x-x_0)+f_y(x_0,y_0)(y-y_0)\\
+\frac{1}{2}\left(f_{xx}(x_0,y_0)(x-x_0)^2+2f_{xy}(x_0,y_0)(x-x_0)(y-y_0)+f_{yy}(x_0,y_0)(y-y_0)^2\right)
f ( x , y ) = f ( x 0 , y 0 ) + f x ( x 0 , y 0 ) ( x − x 0 ) + f y ( x 0 , y 0 ) ( y − y 0 ) + 2 1 ( f x x ( x 0 , y 0 ) ( x − x 0 ) 2 + 2 f x y ( x 0 , y 0 ) ( x − x 0 ) ( y − y 0 ) + f y y ( x 0 , y 0 ) ( y − y 0 ) 2 )
注意还有三次余项。
配方法可以看出是 ( 1 , − 1 , − 2 ) (1,-1,-2) ( 1 , − 1 , − 2 )
L ( x , y , z , λ ) = x y z + λ ( x + y + z − a ) \mathcal L(x,y,z,\lambda)=xyz+\lambda(x+y+z-a)
L ( x , y , z , λ ) = x y z + λ ( x + y + z − a )
可得 x = y = z x=y=z x = y = z
L ( x 1 , x 2 ) = p 1 x 1 + p 2 x 2 + λ ( 2 x 1 α x 2 β − 12 ) \mathcal L(x_1,x_2)=p_1x_1+p_2x_2+\lambda(2x_1^\alpha x_2^\beta-12)
L ( x 1 , x 2 ) = p 1 x 1 + p 2 x 2 + λ ( 2 x 1 α x 2 β − 1 2 )
{ L x 1 = p 1 + ( λ α / x 1 ) Q L x 2 = p 2 + ( λ β / x 2 ) Q L λ = Q − 12 α + β = 1 \left\{
\begin{matrix}
\mathcal L_{x_1}=p_1+(\lambda \alpha/x_1) Q\\
\mathcal L_{x_2}=p_2+(\lambda \beta/x_2) Q\\
\mathcal L_{\lambda}=Q-12\\
\alpha+\beta=1
\end{matrix}
\right.
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ L x 1 = p 1 + ( λ α / x 1 ) Q L x 2 = p 2 + ( λ β / x 2 ) Q L λ = Q − 1 2 α + β = 1
推出
α x 2 p 2 = β x 1 p 1 \alpha x_2 p_2=\beta x_1p_1
α x 2 p 2 = β x 1 p 1
得到:
x 1 = 6 ( p 2 α p 1 β ) β x 2 = 6 ( p 1 β p 2 α ) α x_1=6(\frac{p_2\alpha}{p_1\beta})^\beta\quad x_2=6(\frac{p_1\beta}{p_2\alpha})^\alpha
x 1 = 6 ( p 1 β p 2 α ) β x 2 = 6 ( p 2 α p 1 β ) α
注:分清楚常量和变量,需要认清楚每一个约束条件。
法1:参考 8-22
f ( x , y , z ) = x n F ( y / x , z / x ) f(x,y,z)=x^n F(y/x,z/x)
f ( x , y , z ) = x n F ( y / x , z / x )
已经证明:
( x ∂ ∂ x + y ∂ ∂ y + z ∂ ∂ z ) f ( x , y , z ) = n f ( x , y , z ) \left(x\frac{\partial}{\partial x}+y\frac{\partial }{\partial y}+z\frac{\partial}{\partial z}\right) f(x,y,z)=nf(x,y,z)
( x ∂ x ∂ + y ∂ y ∂ + z ∂ z ∂ ) f ( x , y , z ) = n f ( x , y , z )
法2:
令 u = x t , v = y t , w = z t u=xt,v=yt,w=zt u = x t , v = y t , w = z t x , y , z x,y,z x , y , z t t t
这其实利用了齐次函数的定义:等比例增加 x , y , z x,y,z x , y , z n n n
y 2 + x y + 1 y^2+xy+1
y 2 + x y + 1
怎么对 ∂ 2 f ∂ y 2 \frac{\partial^2 f}{\partial y^2} ∂ y 2 ∂ 2 f x x x
∫ ∂ 2 f ∂ y 2 ∂ y = 2 y + C 1 ( x ) \int\frac{\partial^2 f}{\partial y^2} \partial y=2y+C_1(x)
∫ ∂ y 2 ∂ 2 f ∂ y = 2 y + C 1 ( x )
根据初值,得到
C 1 ( x ) = ∂ f ∂ y ∣ ( x , 0 ) = x C_1(x)=\left.\frac{\partial f}{\partial y}\right|_{(x,0)}=x
C 1 ( x ) = ∂ y ∂ f ∣ ∣ ∣ ∣ ( x , 0 ) = x
因此 ∂ f ∂ y = 2 y + x \frac{\partial f}{\partial y}=2y+x ∂ y ∂ f = 2 y + x
∫ ∂ f ∂ y ∂ y = y 2 + x y + C 2 ( x ) = y 2 + x y + 1 \int\frac{\partial f}{\partial y}\partial y=y^2+xy+C_2(x)=y^2+xy+1
∫ ∂ y ∂ f ∂ y = y 2 + x y + C 2 ( x ) = y 2 + x y + 1
一些引申:
u ( x , y ) = f ( x ) + g ( y ) u(x,y)=f(x)+g(y)
u ( x , y ) = f ( x ) + g ( y )
的充分必要条件是
∂ 2 u ∂ x ∂ y = 0 \frac{\partial ^2 u}{\partial x\partial y}=0
∂ x ∂ y ∂ 2 u = 0
证明:正向显然。反向:
∫ ∂ 2 u ∂ x ∂ y ∂ y = 0 = C 1 ( x ) \int\frac{\partial ^2 u}{\partial x\partial y} \partial y=0=C_1(x)
∫ ∂ x ∂ y ∂ 2 u ∂ y = 0 = C 1 ( x )
因此:
∂ u / ∂ x = C 1 ( x ) \partial u/\partial x=C_1(x)
∂ u / ∂ x = C 1 ( x )
因此
∫ ∂ u ∂ x ∂ x = f ( x ) + C 2 ( y ) = f ( x ) + g ( y ) \int \frac{\partial u}{\partial x}\partial x=f(x)+C_2(y)=f(x)+g(y)
∫ ∂ x ∂ u ∂ x = f ( x ) + C 2 ( y ) = f ( x ) + g ( y )
再回到题目。
正向证明:
u = f g , ∂ 2 u ∂ x ∂ y = f ′ g ′ , ∂ u ∂ x = f ′ g , ∂ u ∂ y = f g ′ u=fg,\frac{\partial^2u}{\partial x\partial y}=f'g',\frac{\partial u}{\partial x}=f'g,\frac{\partial u}{\partial y}=fg'
u = f g , ∂ x ∂ y ∂ 2 u = f ′ g ′ , ∂ x ∂ u = f ′ g , ∂ y ∂ u = f g ′
反向证明:需要观察形式,类似于分式。
u ∂ 2 u ∂ x ∂ y − ∂ u ∂ x ∂ u ∂ y u 2 = ∂ ∂ y ( u x u ) \frac{u\frac{\partial^2 u}{\partial x \partial y}-\frac{\partial u}{\partial x}\frac{\partial u}{\partial y}}{u^2}=\frac{\partial }{\partial y}\left(\frac{u_x}{u}\right)
u 2 u ∂ x ∂ y ∂ 2 u − ∂ x ∂ u ∂ y ∂ u = ∂ y ∂ ( u u x )
则 u x / u u_x/u u x / u y y y φ ( x ) \varphi(x) φ ( x )
ln u = ∫ φ ( x ) d x + C ( y ) \ln u=\int \varphi(x) \mathrm d x+C(y)
ln u = ∫ φ ( x ) d x + C ( y )
即 u u u
题目的简化,f ( x , y , z ) = ln x + 2 ln y + 3 ln z f(x,y,z)=\ln x+2\ln y+3\ln z f ( x , y , z ) = ln x + 2 ln y + 3 ln z f ( x , y , z ) = x y 2 z 3 f(x,y,z)=xy^2z^3 f ( x , y , z ) = x y 2 z 3
得到:
{ x = − 2 λ = r y = − λ = 2 r z = 3 r \left\{
\begin{matrix}
x=\sqrt{-2\lambda}=r\\
y=\sqrt{-\lambda}=\sqrt{2}r\\
z=\sqrt{3}r
\end{matrix}
\right.
⎩ ⎨ ⎧ x = − 2 λ = r y = − λ = 2 r z = 3 r
题目条件两边取对数:
ln a + 2 ln b + 3 ln c ≤ 6 ln ( a + b + c ) − ln 432 \ln a+2\ln b+3\ln c \le 6\ln(a+b+c)-\ln 432
ln a + 2 ln b + 3 ln c ≤ 6 ln ( a + b + c ) − ln 4 3 2
取 a = x 2 , b = y 2 , c = z 2 a=x^2,b=y^2,c=z^2 a = x 2 , b = y 2 , c = z 2
2 ( ln x + 2 ln y + 3 ln z ) ≤ 2 ( ln r + 2 ln 2 r + 3 ln 3 r ) = 2 ( ln r 6 + 1 2 ln 108 ) = 6 ln r 2 + ln 108 − 6 ln 6 = 6 ln ( x 2 + y 2 + z 2 ) − ln 432 2(\ln x+2\ln y+3\ln z)\le 2(\ln r+2\ln \sqrt{2}r+3\ln \sqrt{3}r)\\=2(\ln r^6+\frac{1}{2}\ln 108)\\=6\ln r^2+\ln108-6\ln6\\=6 \ln (x^2+y^2+z^2)-\ln 432
2 ( ln x + 2 ln y + 3 ln z ) ≤ 2 ( ln r + 2 ln 2 r + 3 ln 3 r ) = 2 ( ln r 6 + 2 1 ln 1 0 8 ) = 6 ln r 2 + ln 1 0 8 − 6 ln 6 = 6 ln ( x 2 + y 2 + z 2 ) − ln 4 3 2
通过直线 L L L ( 3 x − 2 y − z − 5 ) + λ ( x + y + z ) = 0 (3x-2y-z-5)+\lambda(x+y+z)=0 ( 3 x − 2 y − z − 5 ) + λ ( x + y + z ) = 0
与曲面相切:设相切于 ( x 0 , y 0 , z 0 ) (x_0,y_0,z_0) ( x 0 , y 0 , z 0 )
{ 3 + λ 4 x 0 = λ − 2 − 4 y 0 = λ − 1 2 ( 3 + λ ) x 0 + ( λ − 2 ) y 0 + ( λ − 1 ) z 0 − 5 = 0 2 x 0 2 − 2 y 0 2 + 2 z 0 = 5 8 \left\{
\begin{matrix}
\frac{3+\lambda}{4x_0}=\frac{\lambda-2}{-4y_0}=\frac{\lambda-1}{2}\\
(3+\lambda)x_0+(\lambda-2)y_0+(\lambda-1)z_0-5=0\\
2x_0^2-2y_0^2+2z_0=\frac{5}{8}
\end{matrix}
\right.
⎩ ⎨ ⎧ 4 x 0 3 + λ = − 4 y 0 λ − 2 = 2 λ − 1 ( 3 + λ ) x 0 + ( λ − 2 ) y 0 + ( λ − 1 ) z 0 − 5 = 0 2 x 0 2 − 2 y 0 2 + 2 z 0 = 8 5
注意沿切向方向有两个方向。
方向导数最大值为梯度的模。

也可以:
4 d x + 2 d y + 2 d z = 0 4 d x + 2 d y − 2 d z = 0 4\mathrm d x+2\mathrm d y+2\mathrm d z=0\\
4\mathrm d x+2\mathrm d y-2\mathrm d z=0
4 d x + 2 d y + 2 d z = 0 4 d x + 2 d y − 2 d z = 0
得到
d x 1 = d y − 2 = d z 0 \frac{\mathrm d x}{1}=\frac{\mathrm d y}{-2}=\frac{\mathrm d z}{0}
1 d x = − 2 d y = 0 d z
即
x − 2 1 = y − 1 − 2 = z − 1 0 \frac{x-2}{1}=\frac{y-1}{-2}=\frac{z-1}{0}
1 x − 2 = − 2 y − 1 = 0 z − 1

选取路径 y = 2 x + x 114514 y=2x+x^{114514} y = 2 x + x 1 1 4 5 1 4
极坐标形式:
lim r → 0 + r 3 cos 2 θ sin θ 2 r cos θ − r sin θ = lim r → 0 + r 2 ⋅ cos 2 θ sin θ 2 cos θ − sin θ \lim_{r\to0^+} \frac{r^3 \cos^2 \theta \sin\theta}{2r\cos\theta-r\sin\theta}=\lim_{r\to0^+} r^2 \cdot \frac{\cos^2\theta\sin\theta}{2\cos\theta-\sin\theta}
r → 0 + lim 2 r cos θ − r sin θ r 3 cos 2 θ sin θ = r → 0 + lim r 2 ⋅ 2 cos θ − sin θ cos 2 θ sin θ
可以令 2 cos θ − sin θ ∼ r 114514 2\cos\theta-\sin\theta \sim r^{114514} 2 cos θ − sin θ ∼ r 1 1 4 5 1 4
分析三角函数的范围,显然分子有一定范围,但是分母能成为 r r r
齐次
x 2 y x 4 + y 2 ⇒ y = k x 2 \frac{x^2y}{x^4+y^2} \Rightarrow y=kx^2
x 4 + y 2 x 2 y ⇒ y = k x 2
分母简单
2 x − y = k x 3 ⇒ y = 2 x − k x 3 2x-y=kx^3 \Rightarrow y=2x-kx^3
2 x − y = k x 3 ⇒ y = 2 x − k x 3

f x y f_{xy} f x y f x f_x f x y y y
f x ( 0 , y ) = lim Δ x → 0 Δ x y ( Δ x 2 − y 2 ) Δ x ( Δ x 2 + y 2 ) = − y f_x(0,y)=\lim_{\Delta x \to 0}\frac{\Delta x y(\Delta x^2-y^2)}{\Delta x(\Delta x^2+y^2)}=-y
f x ( 0 , y ) = Δ x → 0 lim Δ x ( Δ x 2 + y 2 ) Δ x y ( Δ x 2 − y 2 ) = − y
f x y ( 0 , 0 ) = − 1 f_{xy}(0,0)=-1
f x y ( 0 , 0 ) = − 1
因此,可以说明,当混合二阶偏导数不连续的时候,f x y f_{xy} f x y f y x f_{yx} f y x

连续就可以取到最大值和最小值。类比一元函数。

极坐标下一眼可微。

A.

D.

主要是利用对称性,一眼 x , z x,z x , z




梯度模长。




注意到,对于每一个合法的曲线上的点 ( x , y , z ) (x,y,z) ( x , y , z ) f ( x , y ) = 0 f(x,y)=0 f ( x , y ) = 0 x O y xOy x O y

注意是法线方程,方向向量是 τ = ( − 1 , 2 , − 1 ) \boldsymbol \tau=(-1,2,-1) τ = ( − 1 , 2 , − 1 )
x − 3 − 1 = y + 1 2 = z + 5 − 1 \frac{x-3}{-1}=\frac{y+1}{2}=\frac{z+5}{-1}
− 1 x − 3 = 2 y + 1 = − 1 z + 5

比较常规。

其实这种题基本不等式是最快的,完全没有必要拉格朗日乘子。
设 f ( x , y ) f(x,y) f ( x , y ) R 2 \R^2 R 2 lim r → + ∞ ( x ∂ f ∂ x + y ∂ f ∂ y ) = 1 \displaystyle \lim_{r \to +\infin} \left(x\frac{\partial f}{\partial x} +y \frac{\partial f}{\partial y}\right)=1 r → + ∞ lim ( x ∂ x ∂ f + y ∂ y ∂ f ) = 1 r = x 2 + y 2 r=\sqrt{x^2+y^2} r = x 2 + y 2 f ( x , y ) f(x,y) f ( x , y ) R 2 \R^2 R 2

不存在。

C.

算算全微分,结果是
d x + 0 ⋅ d y = 0 \mathrm d x+0\cdot \mathrm d y=0
d x + 0 ⋅ d y = 0
因此是 A.

直接球面坐标。应该是 B.

1 错,考虑凹区域。
2 错,
3 是错的
反例:
f ( x , y ) = { x 2 y x 4 + y 2 , x 2 + y 2 ≠ 0 0 , x 2 + y 2 = 0 f(x,y)=
\left\{
\begin{matrix}
\frac{x^2y}{x^4+y^2} ,x^2+y^2 \not=0\\
0,x^2+y^2=0
\end{matrix}
\right.
f ( x , y ) = { x 4 + y 2 x 2 y , x 2 + y 2 = 0 0 , x 2 + y 2 = 0
设 f ( x , y ) f(x,y) f ( x , y ) f x ( x , y ) , f y ( x , y ) f_x(x,y),f_y(x,y) f x ( x , y ) , f y ( x , y ) ( x 0 , y 0 ) (x_0,y_0) ( x 0 , y 0 ) f ( x , y ) f(x,y) f ( x , y ) ( x 0 , y 0 ) (x_0,y_0) ( x 0 , y 0 ) f ( x , y ) f(x,y) f ( x , y )

exp ( 3 / 2 ) \exp(3/2)
exp ( 3 / 2 )

z u v + z v u = 0 z_{uv}+z_{vu}=0
z u v + z v u = 0
结合 z v u = z u v z_{vu}=z_{uv} z v u = z u v
事实上,最终在说
f ( x , y ) = φ ( x + y ) + ψ ( x − y ) f(x,y)=\varphi(x+y)+\psi(x-y)
f ( x , y ) = φ ( x + y ) + ψ ( x − y )


使用不等式。

简单的。
计算二重极限
lim ( x , y ) → ( ∞ , 3 ) ( 1 + y x ) x 2 x + y 2 \lim_{(x,y) \to(\infin,3)} \left(1+\frac{y}{x}\right)^\frac{x^2}{x+y^2}
( x , y ) → ( ∞ , 3 ) lim ( 1 + x y ) x + y 2 x 2
令 u = 1 / x , v = y − 3 u=1/x,v=y-3 u = 1 / x , v = y − 3
lim ( u , v ) → ( 0 , 0 ) ( 1 + u ( v + 3 ) ) 1 u 2 ( 1 / u + ( v + 3 ) 2 ) = exp lim ( u , v ) → ( 0 , 0 ) 1 u + u 2 ( v + 3 ) 2 u ( v + 3 ) = exp ( 3 ) \lim_{(u,v)\to(0,0)} (1+u(v+3))^\frac{1}{u^2(1/u+(v+3)^2)}=\exp \lim_{(u,v)\to(0,0)} \frac{1}{u+u^2(v+3)^2} u(v+3)=\exp(3)
( u , v ) → ( 0 , 0 ) lim ( 1 + u ( v + 3 ) ) u 2 ( 1 / u + ( v + 3 ) 2 ) 1 = exp ( u , v ) → ( 0 , 0 ) lim u + u 2 ( v + 3 ) 2 1 u ( v + 3 ) = exp ( 3 )

注意是隐函数。



设
( 0 , 0 ) ⇒ ( 2 9 , 0 ) ⇒ ( ( 2 9 ) 2 + 2 9 , 0 ) (0,0)\Rightarrow (\frac{2}{9},0)\Rightarrow ((\frac{2}{9})^2+\frac{2}{9},0) ( 0 , 0 ) ⇒ ( 9 2 , 0 ) ⇒ ( ( 9 2 ) 2 + 9 2 , 0 )
等于证明数列 x n + 1 = x n 2 + 2 9 x_{n+1}=x_n^2+\frac{2}{9} x n + 1 = x n 2 + 9 2
归纳证明 x n < 1 3 x_n<\frac{1}{3} x n < 3 1 x 0 = 0 < 1 3 x_0=0<\frac{1}{3} x 0 = 0 < 3 1 x n + 1 = x n 2 + 2 9 < 1 9 + 2 9 = 1 3 x_{n+1}=x_n^2+\frac{2}{9}<\frac{1}{9}+\frac{2}{9}=\frac{1}{3} x n + 1 = x n 2 + 9 2 < 9 1 + 9 2 = 3 1
然后,证明 x n x_{n} x n 1 3 − x n + 1 = 1 9 − x n 2 = ( 1 3 + x n ) ( 1 3 − x n ) \frac{1}{3}-x_{n+1}=\frac{1}{9}-x_{n}^2=(\frac{1}{3}+x_n)(\frac{1}{3}-x_{n}) 3 1 − x n + 1 = 9 1 − x n 2 = ( 3 1 + x n ) ( 3 1 − x n ) 1 3 + x n < 1 \frac{1}{3}+x_n<1 3 1 + x n < 1 ( 1 3 − x n ) > 1 3 − x n + 1 (\frac{1}{3}-x_n)>\frac{1}{3}-x_{n+1} ( 3 1 − x n ) > 3 1 − x n + 1 x n < x n + 1 x_n<x_{n+1} x n < x n + 1
数列单调增而且有上界,因此存在极限。这里,设极限为 A A A A = 1 3 A=\frac{1}{3} A = 3 1 2 3 \frac{2}{3} 3 2 2 3 \frac{2}{3} 3 2 lim n → + ∞ x n = 1 3 \lim_{n\to+\infin}x_n=\frac{1}{3} lim n → + ∞ x n = 3 1
相当于找到一个边界点,使得这个点恰好不是囿点。
y n + 1 2 = 3 x n 2 y n 2 y_{n+1}^2=3x_n^2y_n^2 y n + 1 2 = 3 x n 2 y n 2
x n + 1 = x n 2 − 3 n y 0 2 ∏ i = 0 n − 1 x i 2 + 2 9 x_{n+1}=x_n^2-3^{n}y_0^2\prod_{i=0}^{n-1} x_{i}^2+\frac{2}{9}
x n + 1 = x n 2 − 3 n y 0 2 i = 0 ∏ n − 1 x i 2 + 9 2
若 y 0 = 0 y_0=0 y 0 = 0 ( 2 3 , 0 ) (\frac{2}{3},0) ( 3 2 , 0 ) δ = 2 3 \delta=\frac{2}{3} δ = 3 2
如果 x n 2 + y n 2 ≤ R 2 x_n^2+y_n^2 \le R^2 x n 2 + y n 2 ≤ R 2 x n + 1 2 + y n + 1 2 ≤ R 2 x_{n+1}^2 + y_{n+1}^2 \le R^2 x n + 1 2 + y n + 1 2 ≤ R 2 O R ⊂ J O_R \sub J O R ⊂ J
C
arctan 3 4 = arccos 4 5 \arctan \frac{3}{4} = \arccos \frac{4}{5}
arctan 4 3 = arccos 5 4
其实取两个特殊点 ( 0 , 1 ) (0,1) ( 0 , 1 ) ( 1 / 2 , 1 / 2 ) (1/2,1/2) ( 1 / 2 , 1 / 2 )
注意带入点值。
x − y − 2 z = 5 x-y-2z=5
x − y − 2 z = 5
原式
y e 2 x 2 + y 2 e − 1 x 2 ≤ y e 2 x 2 ≤ y 2 x 2 + 1 ≤ y x 2 2 \frac{y}{e^\frac{2}{x^2}+y^2e^{-\frac{1}{x^2}}}\le \frac{y}{e^\frac{2}{x^2}}\le \frac{y}{\frac{2}{x^2}+1}\le \frac{yx^2}{2}
e x 2 2 + y 2 e − x 2 1 y ≤ e x 2 2 y ≤ x 2 2 + 1 y ≤ 2 y x 2
当 x = 0 x=0 x = 0
也可以使用基本不等式
∣ f ( x , y ) ∣ = ∣ e 1 / x 2 y e 3 / x 2 + y 2 ∣ = ∣ e 1 / x 2 y 2 e 1.5 / x 2 y ∣ ⋯ |f(x,y)|=\left|\frac{e^{1/x^2}y}{e^{3/x^2}+y^2}\right|=\left|\frac{e^{1/x^2}y}{2e^{1.5/x^2}y}\right| \cdots
∣ f ( x , y ) ∣ = ∣ ∣ ∣ ∣ ∣ e 3 / x 2 + y 2 e 1 / x 2 y ∣ ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ ∣ 2 e 1 . 5 / x 2 y e 1 / x 2 y ∣ ∣ ∣ ∣ ∣ ⋯
A + B + a A+B+a
A + B + a
变换方程:
x = u v , y = u z x = − z v y x 2 x=\frac{u}{v},y=u\\
z_x=-z_v\frac{y}{x^2}
x = v u , y = u z x = − z v x 2 y
z x x = − ( − z v v y x 2 ) y x 2 − z v ( − 2 ) y x 3 = z v v y 2 x 4 + z v 2 y x 3 z_{xx}=-\left(-z_{vv}\frac{y}{x^2}\right)\frac{y}{x^2}-z_{v}(-2)\frac{y}{x^3}\\
=z_{vv}\frac{y^2}{x^4}+z_v\frac{2y}{x^3}
z x x = − ( − z v v x 2 y ) x 2 y − z v ( − 2 ) x 3 y = z v v x 4 y 2 + z v x 3 2 y
z x y = − ( z v v 1 x + z v u ) y x 2 − 1 x 2 z v = − z v v y x 3 − z v u y x 2 − z v 1 x 2 z_{xy}=-\left(z_{vv}\frac{1}{x}+z_{vu}\right)\frac{y}{x^2}-\frac{1}{x^2}z_v\\
=-z_{vv}\frac{y}{x^3}-z_{vu}\frac{y}{x^2}-z_v\frac{1}{x^2}
z x y = − ( z v v x 1 + z v u ) x 2 y − x 2 1 z v = − z v v x 3 y − z v u x 2 y − z v x 2 1
原式:
z v y x 2 − z v u y 2 x 2 = v 2 z v / u − v 2 z v u = 0 ⇒ v 2 ( z v / u − z v u ) = 0 ⇒ z v = z v u u z_v\frac{y}{x^2}-z_{vu}\frac{y^2}{x^2}=v^2z_v/u-v^2z_{vu}=0\\
\Rightarrow v^2(z_v/u-z_{vu})=0\\
\Rightarrow z_v=z_{vu}u
z v x 2 y − z v u x 2 y 2 = v 2 z v / u − v 2 z v u = 0 ⇒ v 2 ( z v / u − z v u ) = 0 ⇒ z v = z v u u
f x ( x , y ) = 32 ( 2 x + 1 ) − 8 ( 2 x + 1 ) 3 f_x(x,y)=32(2x+1)-8(2x+1)^3 f x ( x , y ) = 3 2 ( 2 x + 1 ) − 8 ( 2 x + 1 ) 3
山顶:2 x + 1 = 0 2x+1=0 2 x + 1 = 0 2 x + 1 = 2 2x+1=2 2 x + 1 = 2
f y ( x , y ) = − 64 y f_y(x,y)=-64y f y ( x , y ) = − 6 4 y y = 0 y=0 y = 0
综上,山顶为 ( 1 / 2 , 0 ) (1/2,0) ( 1 / 2 , 0 ) 9 9 9 y = 0 y=0 y = 0 y y y 0 0 0
因此,曲线段为 z = 8 ( 2 x + 1 ) 2 − ( 2 x + 1 ) 4 − 32 y 4 − 7 , x ∈ [ 0 , 1 2 ] , y = 0 z=8(2x+1)^2-(2x+1)^4-32y^4-7,x \in [0,\frac{1}{2}],y=0 z = 8 ( 2 x + 1 ) 2 − ( 2 x + 1 ) 4 − 3 2 y 4 − 7 , x ∈ [ 0 , 2 1 ] , y = 0
看符号即可,选 C C C
B. 构造 F ( x , y , z ) = f ( x , y ) − z F(x,y,z)=f(x,y)-z F ( x , y , z ) = f ( x , y ) − z ( f x , f y , − 1 ) (f_x,f_y,-1) ( f x , f y , − 1 )
C. 求行列式即可,答案是 D.
法向量:
( − 3 sin t , 4 cos t , 1 ) (-3\sin t,4\cos t,1)
( − 3 sin t , 4 cos t , 1 )
因此选 B B B
f ( x , y ) f(x,y) f ( x , y ) O O O ( x , y ) (x,y) ( x , y )
f ( x , y ) = x y f(x,y)=xy f ( x , y ) = x y
lim y → 0 , x = sin y → 0 f ( x , y ) − f ( 0 , 0 ) x 2 − x sin y + sin 2 y = 1 > 0 \lim_{y\to0,x=\sin y \to 0} \frac{f(x,y)-f(0,0)}{x^2-x\sin y+\sin^2y}=1>0
y → 0 , x = sin y → 0 lim x 2 − x sin y + sin 2 y f ( x , y ) − f ( 0 , 0 ) = 1 > 0
因此 I 不成立。
同理,
lim x → 0 , y → 0 f ( x , y ) − f ( 0 , 0 ) x 2 + y 2 = A \lim_{x\to0,y\to0} \frac{f(x,y)-f(0,0)}{x^2+y^2}=A
x → 0 , y → 0 lim x 2 + y 2 f ( x , y ) − f ( 0 , 0 ) = A
也不成立。
这个极限存在只能说明 f ( x , y ) f(x,y) f ( x , y )
II 是在说函数有连续的二阶偏导数,则这两个导数相等。
对于 II 令 g ( h ) = f ( x 0 + h , y 0 + h ) − f ( x 0 + h , y 0 ) − f ( x 0 , y 0 + h ) + f ( x 0 , y 0 ) g(h)=f(x_0+h,y_0+h)-f(x_0+h,y_0)-f(x_0,y_0+h)+f(x_0,y_0) g ( h ) = f ( x 0 + h , y 0 + h ) − f ( x 0 + h , y 0 ) − f ( x 0 , y 0 + h ) + f ( x 0 , y 0 )
令
φ ( x ) = f ( x , y 0 + h ) − f ( x , y 0 ) ψ ( y ) = f ( x 0 + h , y ) − f ( x 0 , y ) \varphi(x)=f(x,y_0+h)-f(x,y_0)\\
\psi(y)=f(x_0+h,y)-f(x_0,y)
φ ( x ) = f ( x , y 0 + h ) − f ( x , y 0 ) ψ ( y ) = f ( x 0 + h , y ) − f ( x 0 , y )
则:
g ( h ) = φ ( x 0 + h ) − φ ( x 0 ) = φ ′ ( x 0 + θ 1 h ) ⋅ h g(h)=\varphi(x_0+h)-\varphi(x_0)=\varphi'(x_0+\theta_1h)\cdot h
g ( h ) = φ ( x 0 + h ) − φ ( x 0 ) = φ ′ ( x 0 + θ 1 h ) ⋅ h
第一次使用拉格朗日中值定理。对 x x x
根据 φ \varphi φ
g ( h ) = ( f x ( x 0 + θ 1 h , y 0 + h ) − f x ( x 0 + θ 1 h , y 0 ) ) h g(h)=(f_x(x_0+\theta_1h,y_0+h)-f_x(x_0+\theta_1h,y_0))h
g ( h ) = ( f x ( x 0 + θ 1 h , y 0 + h ) − f x ( x 0 + θ 1 h , y 0 ) ) h
之后,对 y y y
g ( h ) = f x y ( x 0 + θ 1 h , y 0 + θ 2 h ) h 2 g(h)=f_{xy}(x_0+\theta_1h,y_0+\theta_2h)h^2
g ( h ) = f x y ( x 0 + θ 1 h , y 0 + θ 2 h ) h 2
这里,我们巧妙地把二元转化为了一元函数。
同理,
g ( h ) = f y x ( x 0 + θ 3 h , y 0 + θ 4 h ) h 2 g(h)=f_{yx}(x_0+\theta_3h,y_0+\theta_4h)h^2
g ( h ) = f y x ( x 0 + θ 3 h , y 0 + θ 4 h ) h 2
lim x → 0 , y → 0 f x y f y x \lim_{x\to0,y\to0}\frac{f_{xy}}{f_{yx}}
x → 0 , y → 0 lim f y x f x y
令 h → 0 h \to 0 h → 0
相似的证明:若一阶偏导数连续,则函数可微。
12 d x − 8 d y 12 \mathrm d x-8 \mathrm d y
1 2 d x − 8 d y

注意是单位向量,就是 ( 3 3 , 3 3 , 3 3 ) (\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}) ( 3 3 , 3 3 , 3 3 )
经典的做法,以 λ \lambda λ
x = − λ 2 y = 1 − λ z = 2 λ − 2 x=-\frac{\lambda}{2}\\
y=1-\lambda\\
z=2\lambda-2
x = − 2 λ y = 1 − λ z = 2 λ − 2
推出 λ = 2 / 3 \lambda=2/3 λ = 2 / 3 7 / 3 7/3 7 / 3
本题为实际问题:
在平面 π : x + 2 y − 4 z − 3 = 0 \pi:x+2y-4z-3=0 π : x + 2 y − 4 z − 3 = 0 ( x , y ) (x,y) ( x , y ) ( 0 , 1 , − 2 ) (0,1,-2) ( 0 , 1 , − 2 ) ( x 0 , y 0 , z 0 ) (x_0,y_0,z_0) ( x 0 , y 0 , z 0 )
首先,先直观观察,指数趋近于正无穷,底数虽然极限不存在,但是有范围。
等价于:
exp lim x → 0 , y → 0 3 − x 2 2 y 2 + x y 2 ln ( x 2 y 2 x 4 + y 4 ) \exp \lim_{x\to0,y\to0} \frac{3-x^2}{2y^2+xy^2}\ln \left(\frac{x^2y^2}{x^4+y^4}\right)
exp x → 0 , y → 0 lim 2 y 2 + x y 2 3 − x 2 ln ( x 4 + y 4 x 2 y 2 )
主要是进行放缩。当 − 1 < x < 1 -1 < x <1 − 1 < x < 1
3 − x 2 2 y 2 + x y 2 > 1 3 y 2 \frac{3-x^2}{2y^2+xy^2}>\frac{1}{3y^2}
2 y 2 + x y 2 3 − x 2 > 3 y 2 1
然后对 x 2 y 2 x 4 + y 4 \displaystyle \frac{x^2y^2}{x^4+y^4} x 4 + y 4 x 2 y 2
x 2 y 2 x 4 + y 4 ≤ ( x 4 + y 4 ) / 2 x 4 + y 4 = 1 2 \frac{x^2y^2}{x^4+y^4} \le \frac{(x^4+y^4)/2}{x^4+y^4}=\frac{1}{2}
x 4 + y 4 x 2 y 2 ≤ x 4 + y 4 ( x 4 + y 4 ) / 2 = 2 1
exp ( − ∞ ) = 0 \exp (-\infin)=0
exp ( − ∞ ) = 0
可微的定义:
lim Δ x → 0 , Δ y → 0 h ( x 0 + Δ x , y 0 + Δ y ) − h ( x 0 , y 0 ) − h x ( x 0 , y 0 ) Δ x − h y ( x 0 , y 0 ) Δ y Δ ρ = C o n s t \lim_{\Delta x\to 0,\Delta y\to 0}\frac{h(x_0+\Delta x,y_0+\Delta y)-h(x_0,y_0)-h_x(x_0,y_0)\Delta x-h_y(x_0,y_0)\Delta y}{\Delta \rho}=Const
Δ x → 0 , Δ y → 0 lim Δ ρ h ( x 0 + Δ x , y 0 + Δ y ) − h ( x 0 , y 0 ) − h x ( x 0 , y 0 ) Δ x − h y ( x 0 , y 0 ) Δ y = C o n s t
设下标 N N N ( x 0 + Δ x , y 0 + Δ y ) (x_0+\Delta x,y_0+\Delta y) ( x 0 + Δ x , y 0 + Δ y ) ( x 0 , y 0 ) (x_0,y_0) ( x 0 , y 0 )
原式等于:
f N g N − f g − ( f x g + f g x ) Δ x − ( f y g + f g y ) Δ y f_Ng_N-fg-(f_xg+fg_x)\Delta x-(f_yg+fg_y)\Delta y
f N g N − f g − ( f x g + f g x ) Δ x − ( f y g + f g y ) Δ y
代入(可微推出连续+偏导存在)
f N = f + f x Δ x + f y Δ y + B Δ ρ + o ( Δ ρ ) f_N=f+f_x\Delta x+f_y\Delta y+B\Delta \rho+o(\Delta\rho)
f N = f + f x Δ x + f y Δ y + B Δ ρ + o ( Δ ρ )
(可微的条件)
以及
g N = A + o ( ρ ) g_N=A+o(\rho)
g N = A + o ( ρ )
(极限的条件)
另外:∣ f ( x 0 , y 0 ) ∣ ≤ Δ ρ |f(x_0,y_0)|\le \Delta \rho ∣ f ( x 0 , y 0 ) ∣ ≤ Δ ρ f ( x 0 , y 0 ) = 0 f(x_0,y_0)=0 f ( x 0 , y 0 ) = 0
原式化简为:
( f x Δ x + f y Δ y + o ( Δ ρ ) ) ( A + o ( Δ ρ ) ) − f x g Δ x − f y g Δ y = ( f x Δ x + f y Δ y ) ( A − g ) + A o ( Δ ρ ) (f_x\Delta x+f_y\Delta y+o(\Delta \rho))(A+o(\Delta \rho))-f_xg\Delta x-f_y g\Delta y\\
=(f_x\Delta x+f_y\Delta y)(A-g)+Ao(\Delta \rho)
( f x Δ x + f y Δ y + o ( Δ ρ ) ) ( A + o ( Δ ρ ) ) − f x g Δ x − f y g Δ y = ( f x Δ x + f y Δ y ) ( A − g ) + A o ( Δ ρ )
( A − g ) (A-g) ( A − g ) f x Δ x + f y Δ y f_x\Delta x+f_y \Delta y f x Δ x + f y Δ y Δ ρ \Delta \rho Δ ρ
这样好像走不通,极限不存在。再回到原题,代入一点数进去,比如:
A = 1 , g ( x 0 , y 0 ) = 2 , f ( x , y ) = ( x − x 0 ) 2 + ( y − y 0 ) 2 A=1,g(x_0,y_0)=2,f(x,y)=\sqrt{(x-x_0)^2+(y-y_0)^2}
A = 1 , g ( x 0 , y 0 ) = 2 , f ( x , y ) = ( x − x 0 ) 2 + ( y − y 0 ) 2
发现我们可以构造 w = A , x = x 0 a n d y = y 0 ; g ( x , y ) , e l s e w=A,x=x_0 \mathrm{~and~} y=y_0;g(x,y),\mathrm{else} w = A , x = x 0 a n d y = y 0 ; g ( x , y ) , e l s e
这样 h = f w h=fw h = f w w ( x 0 , y 0 ) = A w(x_0,y_0)=A w ( x 0 , y 0 ) = A

整理为更好看的形式:系数是 f 11 , f 12 f_{11},f_{12} f 1 1 , f 1 2
{ 2 x + a y + 1 = 0 a x + 2 y − 1 = 0 \left\{
\begin{matrix}
2x+ay+1=0\\
ax+2y-1=0
\end{matrix}
\right.
{ 2 x + a y + 1 = 0 a x + 2 y − 1 = 0
线性代数的思想,行列式为 4 − a 2 4-a^2 4 − a 2 0 0 0
d e t ≠ 0 det\not=0 d e t = 0
{ x = − 1 2 − a y = 1 2 − a \left\{
\begin{matrix}
x=\frac{-1}{2-a}\\
y=\frac{1}{2-a}
\end{matrix}
\right.
{ x = 2 − a − 1 y = 2 − a 1
z x x = 2 z y y = 2 z x y = z y x = a z_{xx}=2\quad z_{yy}=2 \quad z_{xy}=z_{yx}=a
z x x = 2 z y y = 2 z x y = z y x = a
Hessian 矩阵需要 a 2 − 4 < 0 a^2-4<0 a 2 − 4 < 0 − 2 < a < 2 -2<a<2 − 2 < a < 2
a = 2 a=2 a = 2
a = − 2 a=-2 a = − 2 x − y + 1 2 = 0 x-y+\frac{1}{2}=0 x − y + 2 1 = 0
z = ( x − y + 1 2 ) 2 + 3 4 z=(x-y+\frac{1}{2})^2+\frac{3}{4}
z = ( x − y + 2 1 ) 2 + 4 3
此时这条直线上都满足极小值。
平时要求求解 Jacobi 行列式,都会给出分母不为 0。
设函数 f ( x , y ) = x 2 + y 4 f(x,y)=\sqrt{x^2+y^4} f ( x , y ) = x 2 + y 4 f ( x , y ) f(x,y) f ( x , y ) ( 0 , 0 ) (0,0) ( 0 , 0 )
显然连续。可导性,对 x , y x,y x , y f x ( 0 , 0 ) f_x(0,0) f x ( 0 , 0 ) f y ( 0 , 0 ) = 0 f_y(0,0)=0 f y ( 0 , 0 ) = 0
研究在一点是否可导,可以研究 φ ( x ) = f ( x , 0 ) = ∣ x ∣ \varphi(x)=f(x,0)=|x| φ ( x ) = f ( x , 0 ) = ∣ x ∣ ψ ( y ) = f ( 0 , y ) = y 2 \psi(y)=f(0,y)=y^2 ψ ( y ) = f ( 0 , y ) = y 2
因为偏导数不存在,所以不可微。这个是固定的逻辑,因为可微的判定需要用到偏导数。



使用柯西不等式:
( 1 + 1 ) ( x 4 + y 4 ) ≥ ( x 2 + y 2 ) 2 ⇒ x 2 + y 2 < 2 ( ( 1 + 1 ) ( x 2 + y 2 ) ) 2 ≥ ( x + y ) 4 ⇒ ( x + y ) 2 < 4 (1+1)(x^4+y^4 )\ge (x^2+y^2)^2 \Rightarrow x^2+y^2 <2 \\
((1+1)(x^2+y^2))^2 \ge (x+y)^4\Rightarrow (x+y)^2 <4
( 1 + 1 ) ( x 4 + y 4 ) ≥ ( x 2 + y 2 ) 2 ⇒ x 2 + y 2 < 2 ( ( 1 + 1 ) ( x 2 + y 2 ) ) 2 ≥ ( x + y ) 4 ⇒ ( x + y ) 2 < 4
因此,取不到 ( − 1 , − 1 ) (-1,-1) ( − 1 , − 1 ) ( 1 , 1 ) (1,1) ( 1 , 1 )
对于 f ( x , y ) f(x,y) f ( x , y )
f ∣ C δ = δ 2 4 − ( 2 x + δ ) 2 f|_{C_\delta}=\frac{\delta^2}{4-(2x+\delta)^2}
f ∣ C δ = 4 − ( 2 x + δ ) 2 δ 2
随 ( 2 x + δ ) 2 (2x+\delta)^2 ( 2 x + δ ) 2
然后在考虑当 x → 1 − , y → 1 − x\to1^-,y \to 1^- x → 1 − , y → 1 − x → − 1 + , y → − 1 + x\to -1^{+},y \to -1^+ x → − 1 + , y → − 1 +
lim ( x , y ) → ( 1 − , 1 − ) ( x − y ) 2 4 − ( x + y ) 2 \lim_{(x,y)\to(1^-,1^-)} \frac{(x-y)^2}{4-(x+y)^2}
( x , y ) → ( 1 − , 1 − ) lim 4 − ( x + y ) 2 ( x − y ) 2
令 u = x − 1 , v = y − 1 u=x-1,v=y-1 u = x − 1 , v = y − 1
lim ( u , v ) → ( 0 , 0 ) ( u − v ) 2 4 − ( u + v + 2 ) 2 = lim ( u , v ) → ( 0 , 0 ) u 2 − 2 u v + v 2 − u 2 − v 2 − 4 u − 4 v − 2 u v \lim_{(u,v) \to (0,0)} \frac{(u-v)^2}{4-(u+v+2)^2}=\lim_{(u,v) \to (0,0)} \frac{u^2-2uv+v^2}{-u^2-v^2-4u-4v-2uv}
( u , v ) → ( 0 , 0 ) lim 4 − ( u + v + 2 ) 2 ( u − v ) 2 = ( u , v ) → ( 0 , 0 ) lim − u 2 − v 2 − 4 u − 4 v − 2 u v u 2 − 2 u v + v 2
再进行极坐标换元:
lim r → 0 r 2 ( 1 − 2 sin θ cos θ ) − r 2 ( 1 + 2 sin θ cos θ ) − 4 r ( sin θ + cos θ ) \lim_{r \to 0} \frac{r^2 (1-2\sin\theta\cos\theta)}{-r^2(1+2\sin\theta\cos\theta)-4r(\sin\theta+\cos\theta)}
r → 0 lim − r 2 ( 1 + 2 sin θ cos θ ) − 4 r ( sin θ + cos θ ) r 2 ( 1 − 2 sin θ cos θ )
需要证明极限 有界 ,而不需要证明极限存在。
设方程 e y + z − x sin z = e e^{y+z}-x\sin z=e e y + z − x sin z = e ( x , y ) = ( 0 , 1 ) (x,y)=(0,1) ( x , y ) = ( 0 , 1 ) z = z ( x , y ) z=z(x,y) z = z ( x , y ) ∂ z ∂ x ∣ ( 0 , 1 ) , ∂ 2 z ∂ x ∂ y ∣ ( 0 , 1 ) \displaystyle \left.\frac{\partial z}{\partial x}\right|_{(0,1)},\left.\frac{\partial ^2 z}{\partial x\partial y}\right|_{(0,1)} ∂ x ∂ z ∣ ∣ ∣ ∣ ( 0 , 1 ) , ∂ x ∂ y ∂ 2 z ∣ ∣ ∣ ∣ ( 0 , 1 )
( d y + d z ) e y + z − sin z d x − x cos z d z = 0 (\mathrm d y+\mathrm d z)e^{y+z}-\sin z\mathrm d x-x\cos z \mathrm d z=0
( d y + d z ) e y + z − sin z d x − x cos z d z = 0
得到
d z = sin z d x e y + z − x cos z + − e y + z d y e y + z − x cos z \mathrm d z=\frac{\sin z\mathrm d x}{e^{y+z}-x\cos z}+\frac{-e^{y+z}\mathrm d y}{e^{y+z}-x\cos z}
d z = e y + z − x cos z sin z d x + e y + z − x cos z − e y + z d y
( x , y ) = ( 0 , 1 ) (x,y)=(0,1) ( x , y ) = ( 0 , 1 ) z = 0 z=0 z = 0 z y = − 1 z_y=-1 z y = − 1
然后对 y y y
z y cos z ( e y + z − x cos z ) − sin z ⋅ e y + z ( 1 + z y ) ( e y + z − x cos z ) 2 \frac{z_y \cos z(e^{y+z}-x\cos z)-\sin z \cdot e^{y+z}(1+z_y)}{(e^{y+z}-x\cos z)^2}
( e y + z − x cos z ) 2 z y cos z ( e y + z − x cos z ) − sin z ⋅ e y + z ( 1 + z y )
后面没有了,前面是
− 1 ⋅ 1 ( e 1 + 0 − 0 ) = − 1 e \frac{-1\cdot 1}{(e^{1+0}-0)}=-\frac{1}{e}
( e 1 + 0 − 0 ) − 1 ⋅ 1 = − e 1
需要搞清楚函数、变量之间的关系,这道题里面,x , y x,y x , y z z z


τ = ( 1 , 0 , 1 ) \boldsymbol \tau=(1,0,1)
τ = ( 1 , 0 , 1 )
∂ u ∂ τ ∣ P 0 = ( 2 2 , 0 , 2 2 ) ⋅ ( 1 7 , 2 7 , 3 7 ) = 2 2 7 \left.\frac{\partial u}{\partial \boldsymbol \tau}\right|_{P_0}=\left(\frac{\sqrt{2}}{2},0,\frac{\sqrt{2}}{2}\right) \cdot \left(\frac{1}{7},\frac{2}{7},\frac{3}{7}\right)=\frac{2\sqrt{2}}{7}
∂ τ ∂ u ∣ ∣ ∣ ∣ P 0 = ( 2 2 , 0 , 2 2 ) ⋅ ( 7 1 , 7 2 , 7 3 ) = 7 2 2
设函数 z = ln x 2 + y 2 z=\ln \sqrt{x^2+y^2} z = ln x 2 + y 2 d z ∣ ( 1 , 1 ) = 1 2 d x + 1 2 d y \mathrm d z|_{(1,1)}=\frac{1}{2} \mathrm d x+\frac{1}{2} \mathrm d y d z ∣ ( 1 , 1 ) = 2 1 d x + 2 1 d y

旋转之后形成了椭球面,方程为:
x 2 4 + y 2 6 + z 2 4 = 1 \frac{x^2}{4}+\frac{y^2}{6}+\frac{z^2}{4}=1
4 x 2 + 6 y 2 + 4 z 2 = 1
3 3 y + 2 2 z = 2 \frac{\sqrt{3}}{3}y+\frac{\sqrt{2}}{2}z=2
3 3 y + 2 2 z = 2
设空间立体 Ω \Omega Ω { ( x , y , z ) ∣ x 2 + z 2 ⩽ 1 } \left\{(x, y, z) \mid x^2+z^2 \leqslant 1\right\} { ( x , y , z ) ∣ x 2 + z 2 ⩽ 1 } { ( x , y , z ) ∣ y 2 + z 2 ⩽ 1 } \left\{(x, y, z) \mid y^2+z^2 \leqslant 1\right\} { ( x , y , z ) ∣ y 2 + z 2 ⩽ 1 } μ ( x , y , z ) = ∣ z ∣ \mu(x, y, z)=|z| μ ( x , y , z ) = ∣ z ∣ M Ω = M_{\Omega}= M Ω =

使用放缩:
lim ( x , y ) → ( 0 , 0 ) x 2 y 4 + x 3 y 3 + x 4 y 2 x 4 + y 4 = lim r → 0 r 2 cos 2 θ sin 4 θ + cos 3 θ sin 3 θ + cos 4 θ sin 2 θ cos 4 θ + sin 4 θ \lim_{(x,y)\to(0,0)}\frac{x^2y^4+x^3y^3+x^4y^2}{x^4+y^4}=\lim_{r\to0}r^2\frac{\cos^2\theta\sin^4\theta+\cos^3\theta\sin^3\theta+\cos^4\theta\sin^2\theta}{\cos^4\theta+\sin^4\theta}
( x , y ) → ( 0 , 0 ) lim x 4 + y 4 x 2 y 4 + x 3 y 3 + x 4 y 2 = r → 0 lim r 2 cos 4 θ + sin 4 θ cos 2 θ sin 4 θ + cos 3 θ sin 3 θ + cos 4 θ sin 2 θ
后面显然有界。
lim ( x , y ) → ( 0 , 0 ) x 2 y 4 x 4 + y 4 + x y x 2 y 2 x 4 + y 4 + y 2 x 4 x 4 + y 4 ≤ x 2 + 1 2 ∣ x y ∣ + y 2 \lim_{(x,y)\to(0,0)} x^2 \frac{y^4}{x^4+y^4}+xy\frac{x^2y^2}{x^4+y^4}+y^2\frac{x^4}{x^4+y^4} \le x^2+\frac{1}{2}|xy|+y^2
( x , y ) → ( 0 , 0 ) lim x 2 x 4 + y 4 y 4 + x y x 4 + y 4 x 2 y 2 + y 2 x 4 + y 4 x 4 ≤ x 2 + 2 1 ∣ x y ∣ + y 2

还可以直接利用公式:
∂ z ∂ x = − F x F z = − − 2 x e z − 2 y \frac{\partial z}{\partial x}=-\frac{F_x}{F_z}=-\frac{-2x}{e^z-2y}
∂ x ∂ z = − F z F x = − e z − 2 y − 2 x
∂ 2 z ∂ x ∂ y = − 2 x ( e z z y − 2 ) ( e z − 2 y ) 2 \frac{\partial^2 z}{\partial x\partial y}=-\frac{2x(e^zz_y-2)}{(e^z-2y)^2}
∂ x ∂ y ∂ 2 z = − ( e z − 2 y ) 2 2 x ( e z z y − 2 )

几何意义,画图求解。
计算极限
lim ( x , y ) → ( 0 , 0 ) cos 2 y − 1 ( 2 + x ) y 2 \lim_{(x,y) \to (0,0)} \frac{\sqrt{\cos 2y}-1}{(2+x)y^2}
( x , y ) → ( 0 , 0 ) lim ( 2 + x ) y 2 cos 2 y − 1
如果 x , y x,y x , y
lim x → 0 f ( x ) , lim y → 0 g ( y ) \lim_{x \to 0} f(x),\lim_{y \to 0}g(y)
x → 0 lim f ( x ) , y → 0 lim g ( y )
判别函数 ( 2 x + 1 ) y − 1 x 2 + 2 y 2 \displaystyle \frac{(2x+1)^y -1}{x^2+2y^2} x 2 + 2 y 2 ( 2 x + 1 ) y − 1 ( 0 , 0 ) (0,0) ( 0 , 0 )
上下次数相等,极限大概率不存在。
赋值和求导可交换顺序,可以将被求偏导变量之外的变量先代入,然后再求导。

判别函数
f ( x , y ) = { x 3 y , y ≠ 0 0 , y = 0 f(x,y)=\left\{
\begin{matrix}
\frac{x^3}{y},y\not=0\\
0,y=0
\end{matrix}
\right.
f ( x , y ) = { y x 3 , y = 0 0 , y = 0
在 ( 0 , 0 ) (0,0) ( 0 , 0 )
可微判别的条件。
lim ( x , y ) → ( 0 , 0 ) x 3 y x 2 + y 2 \lim_{(x,y) \to (0,0)} \frac{x^3}{y\sqrt{x^2+y^2}}
( x , y ) → ( 0 , 0 ) lim y x 2 + y 2 x 3
不存在,取 y = x 2 y=x^2 y = x 2
lim ( x , y ) → ( 0 , 0 ) 1 1 + x 2 = 1 \lim_{(x,y) \to (0,0)} \frac{1}{\sqrt{1+x^2}}=1
( x , y ) → ( 0 , 0 ) lim 1 + x 2 1 = 1
取 y = − x 2 y=-x^2 y = − x 2 − 1 -1 − 1
这题的证明方法比较特殊
或者,也可以取极坐标代换,得到
r cos 3 θ sin θ r\frac{\cos^3 \theta}{\sin\theta}
r sin θ cos 3 θ
显然后面一项是无界的。因此,不存在极限。
先赋值,再计算。
设 f ( x , y ) = ∫ 0 x y ( e − t 2 + 1 ) d t \displaystyle f(x,y)=\int_0^{xy} (e^{-t^2}+1)\mathrm d t f ( x , y ) = ∫ 0 x y ( e − t 2 + 1 ) d t
y [ ( 1 − 4 x 2 y 2 ) e − x 2 y 2 + 1 ] y[(1-4x^2y^2) e^{-x^2y^2}+1]
y [ ( 1 − 4 x 2 y 2 ) e − x 2 y 2 + 1 ]

求函数
f ( x , y ) = { x 3 y , y ≠ 0 0 , y = 0 f(x,y)=\left\{
\begin{matrix}
\frac{x^3}{y},y\not=0\\
0,y=0
\end{matrix}
\right.
f ( x , y ) = { y x 3 , y = 0 0 , y = 0
在 ( 0 , 0 ) (0,0) ( 0 , 0 ) l \boldsymbol l l
∂ f ∂ l ∣ ( 0 , 0 ) \left. \frac{\partial f}{\partial \boldsymbol l}\right|_{(0,0)}
∂ l ∂ f ∣ ∣ ∣ ∣ ( 0 , 0 )
还是需要利用方向导数的定义,若 l \boldsymbol l l y y y 0 0 0
否则,
∂ f ∂ l ∣ ( 0 , 0 ) = lim t → 0 f ( t cos α , t cos β ) t = 0 \left. \frac{\partial f}{\partial \boldsymbol l}\right|_{(0,0)}=\lim_{t \to 0} \frac{f(t \cos \alpha,t \cos \beta)}{t}=0
∂ l ∂ f ∣ ∣ ∣ ∣ ( 0 , 0 ) = t → 0 lim t f ( t cos α , t cos β ) = 0
哪怕方向导数每个方向都存在,仍然不能保证函数可微。

注意化为单位向量。
求曲线 { x = 2 t − sin t , y = 1 − cos t , z = 4 sin t 2 \left\{\begin{array}{c}x=2 t-\sin t, \\ y=1-\cos t, \\ z=4 \sin \frac{t}{2}\end{array}\right. ⎩ ⎨ ⎧ x = 2 t − sin t , y = 1 − cos t , z = 4 sin 2 t t = π 2 t=\frac{\pi}{2} t = 2 π
比较简单
∇ ( x , y , z ) = ( d x , d y , d z ) \nabla(x,y,z)=(\mathrm d x,\mathrm d y,\mathrm d z)
∇ ( x , y , z ) = ( d x , d y , d z )
已知曲面 z = λ x y ( λ > 0 ) \displaystyle z=\frac{\lambda}{xy}(\lambda>0) z = x y λ ( λ > 0 ) x 2 4 + y 2 4 + z 2 = 1 \displaystyle \frac{x^2}{4}+\frac{y^2}{4}+z^2=1 4 x 2 + 4 y 2 + z 2 = 1 λ \lambda λ
相当于求 λ = x y z \lambda =xyz λ = x y z
1 = x 2 4 + y 2 4 + z 2 ≥ 3 x 2 y 2 z 2 16 3 = 3 λ 2 16 3 1=\frac{x^2}{4}+\frac{y^2}{4}+z^2 \ge 3 \sqrt[3]{\frac{x^2y^2z^2}{16}}=3\sqrt[3]{\frac{\lambda^2}{16}}
1 = 4 x 2 + 4 y 2 + z 2 ≥ 3 3 1 6 x 2 y 2 z 2 = 3 3 1 6 λ 2


设 u = y , v = y x u=y,v=\frac{y}{x} u = y , v = x y x ∂ 2 z ∂ x 2 + y ∂ 2 z ∂ x ∂ y \displaystyle x \frac{\partial^2 z}{\partial x^2}+y\frac{\partial^2 z}{\partial x\partial y} x ∂ x 2 ∂ 2 z + y ∂ x ∂ y ∂ 2 z u , v u,v u , v z z z
得到
z v = z v u ⋅ u z_v=z_{vu}\cdot u
z v = z v u ⋅ u
这种变换的结果一般都比较简单。
确定椭球 x 2 + y 2 + z 2 8 = 1 \displaystyle x^2+y^2+\frac{z^2}{8}=1 x 2 + y 2 + 8 z 2 = 1 P 0 P_0 P 0 P 0 P_0 P 0

Lagrange 乘数法也简单。
设二元连续函数 f ( x , y ) f(x,y) f ( x , y )
lim ( x , y ) → ( 0 , 0 ) ∫ 0 1 f ( t x , t y ) d t x 2 + y 2 = A \lim_{(x,y) \to (0,0)} \frac{\int_0^1 f(tx,ty)\mathrm d t}{\sqrt{x^2+y^2}}=A
( x , y ) → ( 0 , 0 ) lim x 2 + y 2 ∫ 0 1 f ( t x , t y ) d t = A
其中 A A A f x ( 0 , 0 ) f_x(0,0) f x ( 0 , 0 ) f y ( 0 , 0 ) f_y(0,0) f y ( 0 , 0 )
偏导数的定义
f x ( x , y ) = lim Δ x → 0 f ( x + Δ x , y ) − f ( x , y ) Δ x f_x(x,y)=\lim_{\Delta x \to0} \frac{f(x+\Delta x,y)-f(x,y)}{\Delta x}
f x ( x , y ) = Δ x → 0 lim Δ x f ( x + Δ x , y ) − f ( x , y )
当 y = 0 y=0 y = 0
A = lim x → 0 ∫ 0 1 f ( t x , 0 ) d ( t x ) x ∣ x ∣ = x > 0 lim x → 0 + ∫ 0 x f ( u ) d u x 2 = L lim x → 0 + f ( x ) 2 x = 1 2 f x ( 0 , 0 ) A=\lim_{x \to0} \frac{\int_0^1 f(tx,0)\mathrm d (tx)}{x|x|}\overset{x>0}{=}\lim_{x\to0^+} \frac{\int_0^x f(u)\mathrm d u}{x^2} \overset{\mathcal L}{=} \lim_{x\to0^+} \frac{f(x)}{2x}=\frac{1}{2}f_x(0,0)
A = x → 0 lim x ∣ x ∣ ∫ 0 1 f ( t x , 0 ) d ( t x ) = x > 0 x → 0 + lim x 2 ∫ 0 x f ( u ) d u = L x → 0 + lim 2 x f ( x ) = 2 1 f x ( 0 , 0 )
取 x → 0 − x\to0^- x → 0 − A = − 1 2 f x ( 0 , 0 ) A=-\frac{1}{2} f_x(0,0) A = − 2 1 f x ( 0 , 0 ) A = 0 A=0 A = 0
若 f ( 0 , 0 ) ≠ 0 f(0,0) \not=0 f ( 0 , 0 ) = 0 f ( 0 , 0 ) > 0 f(0,0)>0 f ( 0 , 0 ) > 0 f ( x , y ) f(x,y) f ( x , y ) ε \varepsilon ε
利用积分中值定理,存在某个常数 ξ ∈ [ 0 , 1 ] \xi \in[0,1] ξ ∈ [ 0 , 1 ]
∫ 0 1 f ( t x , t y ) = f ( ξ x , ξ y ) \int_0^1 f(tx,ty)=f(\xi x,\xi y)
∫ 0 1 f ( t x , t y ) = f ( ξ x , ξ y )
因此,
lim ( x , y ) → ( 0 , 0 ) f ( ξ x , ξ y ) x 2 + y 2 = A \lim_{(x,y) \to(0,0)} \frac{f(\xi x,\xi y)}{\sqrt{x^2+y^2}}=A
( x , y ) → ( 0 , 0 ) lim x 2 + y 2 f ( ξ x , ξ y ) = A

设平面区域 D = { ( x , y ) ∣ x 2 ≤ 2 y ≤ 3 } D=\{(x,y) \mid x^2 \le 2y \le 3\} D = { ( x , y ) ∣ x 2 ≤ 2 y ≤ 3 } [ x ] [x] [ x ] x x x
∬ D ( [ 2 y − x 2 ] ) 2 d σ \iint_D ([2y-x^2])^2 \mathrm d \sigma
∬ D ( [ 2 y − x 2 ] ) 2 d σ
分为三个部分计算:
\int_{-\sqrt{3}}^\sqrt{3} (1.5-\frac{x^2}{2})\mathrm d x \quad \int_{-\sqrt{2}}^\sqrt{2} (1 - \frac{x^2}{2}) \mathrm d x \quad \int_{-1}^1 (0.5-\frac{x^2}{2})\mathrm d x
设函数 f ( x , y ) f(x,y) f ( x , y ) D = { ( x , y ) ∣ 0 ≤ x , y ≤ 1 } D=\{(x,y)\mid 0\le x,y\le 1\} D = { ( x , y ) ∣ 0 ≤ x , y ≤ 1 } ∀ ( x 0 , y 0 ) ∈ D \forall (x_0,y_0) \in D ∀ ( x 0 , y 0 ) ∈ D f ( x 0 , y ) f(x_0,y) f ( x 0 , y ) f ( x , y 0 ) f(x,y_0) f ( x , y 0 ) f ( x , y ) f(x,y) f ( x , y ) D D D
连续的定义:
lim ( x , y ) → ( x 0 , y 0 ) f ( x , y ) − f ( x 0 , y 0 ) = lim ( x , y ) → ( x 0 , y 0 ) ( f ( x , y ) − f ( x , y 0 ) ) + lim ( x , y ) → ( x 0 , y 0 ) ( f ( x , y 0 ) − f ( x 0 , y 0 ) ) = 0 \lim_{(x,y) \to (x_0,y_0)} f(x,y)-f(x_0,y_0)\\=\lim_{(x,y) \to (x_0,y_0)} (f(x,y)-f(x,y_0))+\lim_{(x,y) \to (x_0,y_0)} (f(x,y_0)-f(x_0,y_0))\\
=0
( x , y ) → ( x 0 , y 0 ) lim f ( x , y ) − f ( x 0 , y 0 ) = ( x , y ) → ( x 0 , y 0 ) lim ( f ( x , y ) − f ( x , y 0 ) ) + ( x , y ) → ( x 0 , y 0 ) lim ( f ( x , y 0 ) − f ( x 0 , y 0 ) ) = 0
题目条件过强?