物理强基内容

重要的思想方法

微元法

速度和加速度都是由微元法定义的，其中 $v=\frac{\Delta x}{\Delta t},a=\frac{\Delta v}{\Delta t}$ 。

我们常常使用近似： $\Delta l=\Delta \theta \times r$ ，其中 $l$ 是近似的弧长。这个方法可以直接求得匀速圆周运动物体的加速度，也可以求一些速度方向改变物体的加速度。

$(1+\alpha)^n=1+n\alpha$ 。 $\alpha$ 正负无关。

$(1+\alpha)^{-1}=1-\alpha$ 。

求导法

v\cos \omega t=\omega R = \omega \frac{h}{\cos \omega t}\\ v=\frac{\omega h}{\cos^2 \omega t}\\ a=\frac{\text{d} v}{\text{d} t}=\omega h \times \frac{\text{d}(\frac{1}{\cos^2\omega t})}{\text{d} t}= \frac{2\omega^2 h \sin\omega t}{\cos^3\omega t}

运动的合成与分解

\begin{aligned} x&=v_0\cos\theta t\\ y&=v_0\sin\theta t-\frac{1}{2}gt^2 \end{aligned}

在斜面上就沿斜面方向分解。
注意与能量的关系结合。

静力学、牛顿运动定律

力平衡+力矩平衡，三力汇交原理。

轻杆的性质：永远平衡（力+力矩）

加速度关联类的问题：找位移关系。先假设一个物体不动，再假设另外一个物体不动，加速度关系是两者的合成。

惯性力

\sum \vec F = m \vec a_{相} + m \vec a_牵\\ \sum \vec F - m \vec a_牵 = m \vec a_{相}\\ \vec{F^*}=m\vec a_牵

斜面自由滑下等效重力加速度为 $g\cos \theta$ 可以惯性力验证。

动量和能量

看系统受哪个方向的力，则系统在垂直于这个力的方向动量守恒。

冲量分析问题

设速度未知数（矢量分解的原则，注意单一方向的物体）
沿绳的速度相等
动量守恒

斜碰

分解为法向速度。

质点系

约化质量：

m=\frac{m_1m_2}{m_1+m_2}

天体运动

角动量

L=mvr\sin\theta

与参考点有关。

开普勒第二定律和机械能守恒结合：

\left\{ \begin{aligned} &vr\sin\theta=const\\ &\frac{1}{2}mv^2-\frac{GMm}{r}=E(const) \end{aligned} \right.

E=\left\{ \begin{aligned} &-\frac{GMm}{2a}, eclipse \\ &0,parabola\\ &\frac{GMm}{2a},hyperbola \end{aligned} \right.

轨道是连续的，不会改变轨道与原轨道没有交点。

双星问题

常常以其中一个天体作为参考系。

振动

简谐振动

找到平衡点
设一段小位移
$\Delta F=-k \Delta x$ ，忽略二阶小量。
$T=2\pi\sqrt{\frac{m}{k}}$ 。

p_l=\frac{v_0}{v_0+Sx} p_0,p_r=\frac{v_0}{v_0-Sx}p_0\\ F=(p_l-p_r)S=p_0Sv_0\frac{-2Sx}{v_0^2-(Sx)^2}=-\frac{2p_0S^2}{v_0}x

自由振子分析

运动的合成与分解思想，匀速直线运动+简谐振动。

直接 $m=\mu$ 约化质量， $T=2\pi\sqrt{\frac{m_Am_B}{(m_A+m_B)k}}$ 。

或者以质心系分析， $k'=\frac{m_A+m_B}{m_B}k$ 。

简谐振动的总能量： $E=\frac{1}{2}kA^2,E_k=E\sin^2(\omega t+\varphi),E_p=E\cos^2(\omega t+\varphi)$ 。

分析自由振子， $E_k$ 在质心系中观察，即为 $E_k=\frac{1}{2} \mu v_相^2$ 。

弹簧和动量守恒结合，对时间 $t$ 积分，可以得到位移关系、弹簧压缩的长度之间的关系。

径向振动

受有心力场的作用，利用好 $L=mvr\sin\theta=const$ 。

刚体

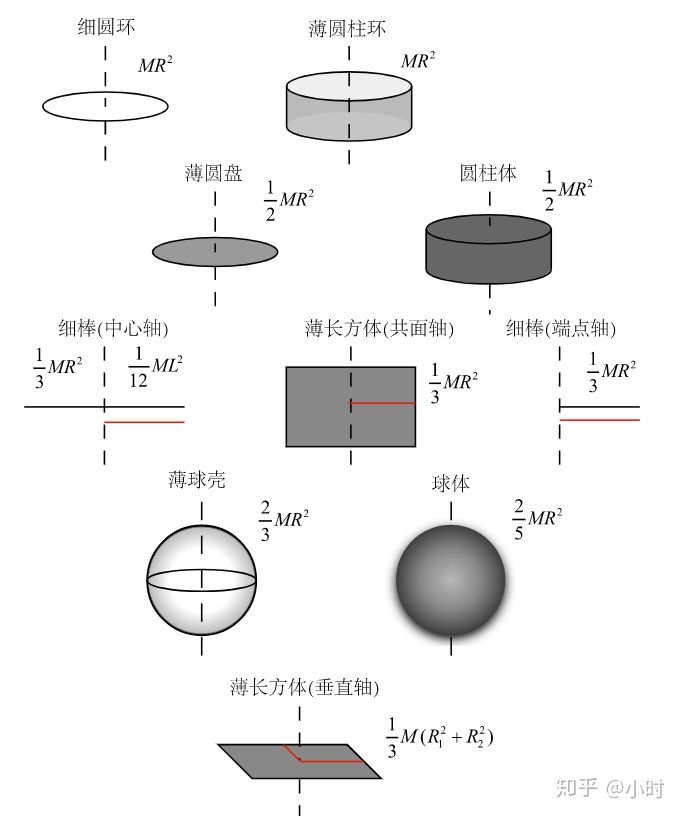
无滑动滚动： $v=\omega r,a=\beta R$ 。

再列两个式子，第一个是作为整体的牛二，第二个是 $\sum M=I\beta$ ，两个式子表明了力的不同作用效果，一种改变物体的平动运动状态，另外一种改变物体的转动状态。

静电场

如果是有心力场，注意运用角动量守恒。

静电现象

静电平衡

导体内部无电场，导体是一个等势体，导体内部产生的感应电场要与外部的电场平衡。
导体的电荷全部分布在表面，否则导体的内部就会有电场
导体表面电场垂直于表面，否则导体表面的电荷就会移动

静电屏蔽

无论导体接地与否，导体外部的电荷都不会影响腔内的电场分布。
若导体接地，则腔内的电荷不会影响导体外部的电场分布。
若导体不接地，则腔内的电荷会影响导体外部的电场分布。
腔内的电荷对导体外部的电荷分布也没有影响。
腔内的电荷相当于腔内部表面的电荷

具体可以用高斯定理+电荷守恒分析。

高斯定理

\oiint E \Delta S = \frac{\sum q}{\varepsilon_0}

E=\frac{\sigma}{\varepsilon_0} (k=\frac{1}{4\pi\varepsilon_0})

高斯定理运用最好选择对称的闭合曲面，如圆柱体、球体，以保证 $E$ 一致。

运用

求无限大线密度 $\lambda$ 的细长导线距离 $r$ 处的电场强度。

$E \times 2\pi rl=\frac{l\lambda}{\varepsilon_0}$ 。
求无限大面密度 $\sigma$ 导体平板两侧电场强度。

$2ES=\frac{S\sigma}{\varepsilon_0}$ 。这里的面密度两边都要算，因此比正常的多除了 $2$ 。

环路定理

\sum E \Delta l \cos \theta =0

电势能

W=\frac{1}{2}\sum q_i \varphi_i

电像法

将感应电荷激发的电场等效于点电荷激发的电场。

电介质

C=\frac{\varepsilon_r S}{4\pi kd}=\frac{\varepsilon_0\varepsilon_r S}{d} \quad \varepsilon = \varepsilon_0 \varepsilon_r

磁场

安培环路定理

\oint B \text{d}l=\mu_0 \sum I_i=\mu_0 \iint_S j \text{d}S

取 $B$ 在 $\text{d}l$ 上的投影长度。

无限长通电螺线管产生的磁场强度 $B=\mu_0nI$ ，其中 $n$ 代表单位长度的线圈匝数。

因为内部的面积有限，而外部的面积无限，外部的磁感应强度看做 0，而对于内部，取一不包含电流的环路，得到 $B$ 是均匀的。

磁场高斯定理

\oiint_{(S)} B \text{d}S=0

热学

理想气体

只有分子动能，没有分子势能。

pV=nRT \\ U=\frac{i}{2}nRT

$i$ 代表自由度。

$i=3$ 单原子分子气体，速度有 $x,y,z$ 轴三个方向的自由度。
$i=5$ 双原子分子气体，有 $x,y,z$ 三个方向自由度和两个转动自由度。
$i=6$ 多原子分子气体，三个转动自由度，三个平动自由度。

热力学第一定律

这里的 $W$ 是气体对外做的功。

Q=W+\Delta U

\begin{aligned} \text{d}Q&=\text{d}W+\text{d}U\\ &=p\text{d}V+\frac{i}{2}nR\text{d}T \end{aligned}

求理想气体经历热力学过程 $p=kV$ ，对应的 $C$ ，已知 $R,C_V$ 。

摩尔热容 $C$ ，摩尔等体积热容 $C_V$ （ $V$ 不变）：

C=\frac{\text{d} Q}{n \text{d} T}

\text{d}W=0\\ \text{d}Q=\text{d}U=\frac{i}{2}nR\text{d}T=nC_V\text{d}T

那么 $C_V=\frac{i}{2}R$ 。

nRT=pV=kV^2\\ nR\text{d}T=k\text{d}(V^2)=2kV\text{d}V\\ kVdV=\frac{1}{2}nRdT

C=\frac{\text{d}Q}{n\text{d}T}=\frac{\text{d}W+\text{d}U}{n\text{d}T}=\frac{p\text{d}V+nC_V\text{d}T}{n\text{d}T}=\frac{1}{2}R+C_V

若是 $p=kV^{\alpha}$ ，则 $C=\frac{1}{\alpha+1}R+C_V$ 。

经常用到 $\alpha=0,1,+\infty$ 的情况，其中 $\infty$ 对应 $V$ 不变。

循环过程

系统从某一状态出发，经过一系列准静态过程之后又回到了初态，称为循环过程。

顺时针：正循环，热机（热量转化为机械功），逆时针：逆循环，制冷机（机械功移动热量）。

Q_{吸}=W+Q_{放}\\ \eta=\frac{W}{Q_{吸}}=\frac{Q_{吸}-Q_{放}}{Q_吸}=1-\frac{Q_放}{Q_吸}

Q_{吸}=\int p\text{d}V=nRT\int_{V_A}^{V_B} \frac{\text{d}V}{V}=nRT_1 \ln\frac{V_{A}}{V_B}\\ Q_{放}=nRT_2 \ln\frac{V_{C}}{V_D}

而绝热过程 $p=kV^\alpha$ ，得到 $V_A/V_B=V_C/V_D$ ，效率 $\eta=1-\frac{T_1}{T_2}$ ，卡诺循环。

例题

奥托循环，等体、绝热、等体、绝热。

$Q_吸=\frac{i}{2}nR(T_B-T_A)=\frac{i}{2}V_2(P_B-P_A)$