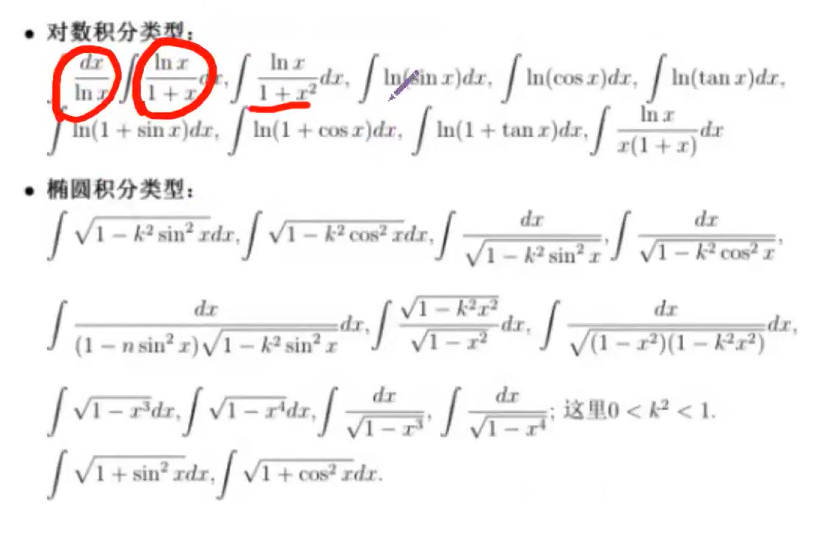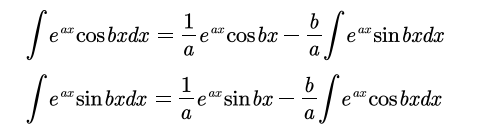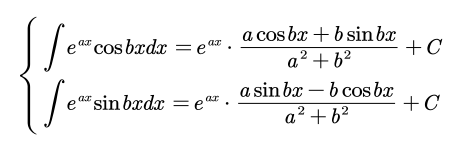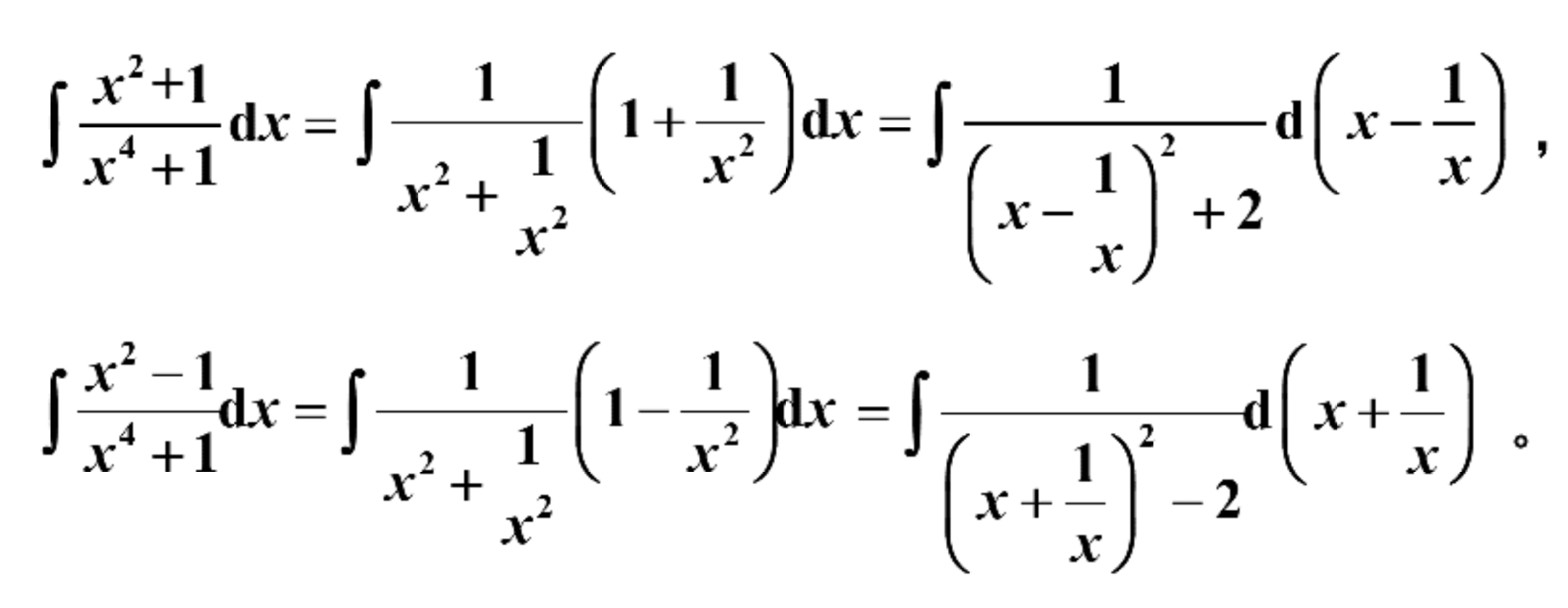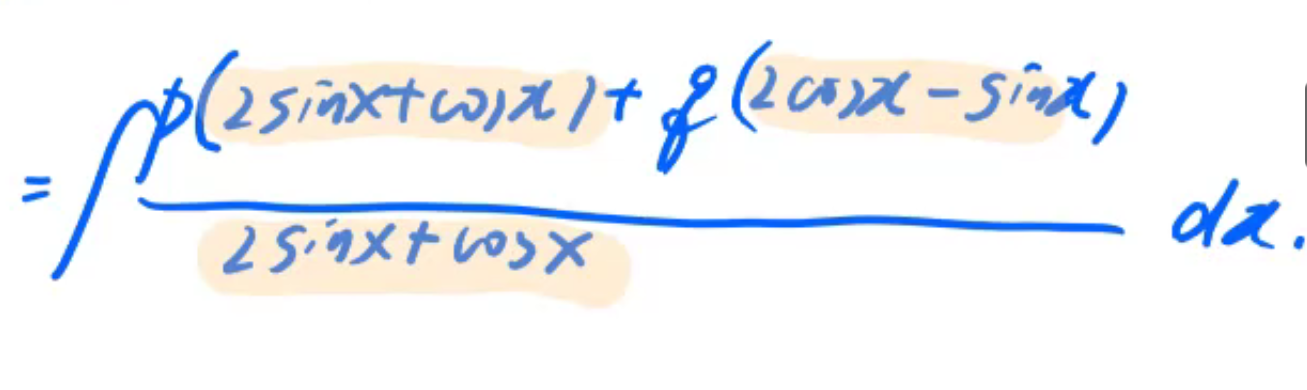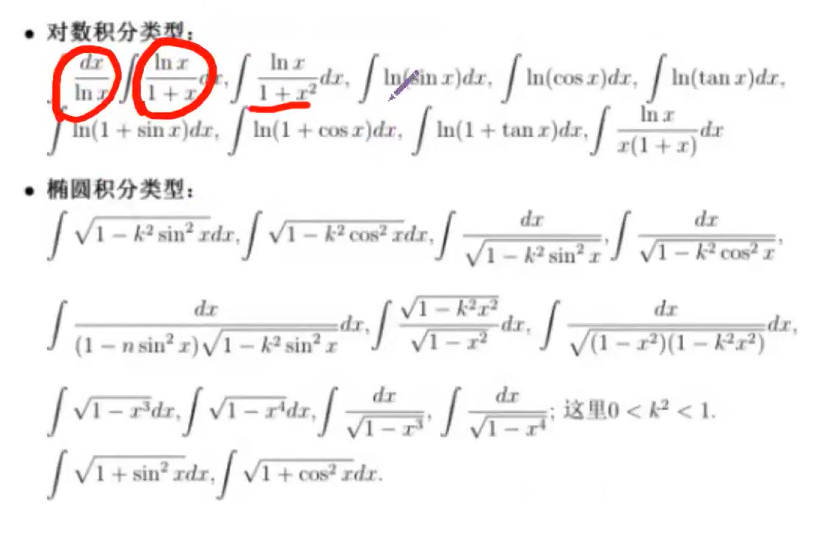一些经常用到的原函数
sec2x⇒tanx,csc2x⇒−cotx
x2+ax⇒x2+a
一些需要记忆的基本不定积分
∫tanxdx=−ln∣cosx∣+C,∫cotxdx=ln∣sinx∣+C
∫a2+x21dx=a1arctan(ax)+C∫a2+x21dx=ln(x+a2+x2)+C(注意是x)
∫a2−x21dx=2a1ln∣∣∣∣x−ax+a∣∣∣∣+C∫a2−x21=arcsin(ax)+C
∫x2−a21dx=ln∣x+x2−a2∣+C∫x2−a21=−2a1ln∣∣∣∣x−ax+a∣∣∣∣+C
∫secxdx=∫secx+tanxsec2x+secxtanxdx=ln∣secx+tanx∣+C∫cscxdx=ln∣cscx−cotx∣+C
∫tan2xdx=∫(sec2x−1)dx=tanx−x+C
∫sinx1⇒lntan2x+C
∫02a∣x2−a2∣1dx
这就需要我们分段讨论。
积分的线性性
∫f+gdx=∫fdx+∫gdx
拆分分子。
第一类换元法
总结为识别出换元的形式。
∫f[φ(x)]φ′(x)dx=∫f[φ(x)]d[φ(x)]=F(φ(x))+C
本质在于换元。我们常用:
∫f(ax+b)dx=a1∫f(ax+b)d(ax+b)
一个技巧是构造:
∫ff′dx
如:
∫secxdx=∫secx+tanxsec2x+secxtanxdx=ln∣secx+tanx∣+C∫cscxdx=ln∣cscx−cotx∣+C∫tanxdx=ln∣cosx∣+C
凑微分法
这里和积分有点不一样,是比较简易型的求原函数,如:
dx=a1d(ax+b)(a=0)
xdx=21d(x2±a2)=−21d(a2−x2)
sinxdx=−dcosx
cosxdx=dsinx
x1dx=dln∣x∣
exdx=dex
第二类换元法
总结为主动换元。令 x=φ(t),其中,不一定要强制代入反函数,可以观察形式,列出方程,来求解,但是需要千万注意的是最后的答案不能含 t。
∫f(x)dx=∫f[φ(t)]φ′(t)dt=F(t)+C=F(φ−1(x))+C
处理 x2±a2,a2±x2 可以三角代换。
- x2+a2,令 x=atant,则 x2+a2=asect。
- x2−a2,令 x=asect,则 x2−a2=atant。
- a2−x2,令 x=acost,则 a2−x2=asint。
回代过程中我们经常遇到各种反三角函数,它们的关系是:
\arcsin x+\arccos x=\frac{\pi}{2}=C \\
\arcsec x =\arccos \frac{1}{x},\arccsc x=\arcsin\frac{1}{x}\\
\arctan x + \arctan \frac{1}{x} = \frac{\pi}{2}=C
求:
∫x2+a2dx=∫asectd(atant)=∫sectdt=ln∣sect+tant∣+C=ln∣x+x2+a2∣+C
这个结果可以记忆。
类似的:
∫x2±a2dx=ln∣x+x2±a2∣+C
求:
∫a2−x2dx=2a2∫(1+cos2t)dt=2a2t+2a2sintcost+C
注意到 t=arcsinax,cos2t+sin2t=1,cost=aa2−x2,代入即可得到:
∫a2−x2dx=2a2arcsinax+2xa2−x2+C
这个结果可以记忆。
现在我们还差 ∫a2+x2dx 没求,这个结果会在分部积分里面讲到。也可以:
x=tant,∫a2+x2dx=a2∫sec3tdt=21(xa2+x2+a2ln(a2+x2+x))+C
求:
∫a1x2+b1x+c1b2x+c2dx
一般化为 α∫a1x2+b1x+c12a1x+b1dx+β∫a1x2+b1x+c11dx。前面就是 α/2a1x2+b1x+c1,后面可以转化为 ∫x2±a2dx 的形式。
倒置换
求:
∫xax2+bx+c1dx
使用 倒置换,令 x=t1,则:
∫xax2+bx+c1dx=∫t1t2a+tb+c−t21dt=−∫ct2+bt+adt
然后继续换元。比如说把分子变成 (mx+n)+p2 的形式,然后再转换为 p(pmx+pn)2+1。
一般是看到分母的次数比较高,就要使用倒置换
求不定积分:
∫x(1−x)dx
转换为:
∫41−(21−x)2dx=2∫1−(1−2x)2dx=−∫1−(1−2x)2d(1−2x)=arcsin(1−2x)+C
这种题还有特殊做法,当分子可以因式分解为 (x−a)(b−x),可以换元 x=asin2t+bcos2t。
求
∫xx2+px+qdx
凑 d(x2+px+q)。
二倍角公式换元
cosx+1=2cos22x
如果在分子上,想要降次,则右推左,如果在分母上,想要拆项,则左推右,如:
∫cos2xdx,∫xcos2xdx
∫1+cosxx+sinxdx
这个换元的核心思想是:如果换元在分子上,我们可以通过拆分积分的方式,得到几个比较简单的子积分,但是在分母上,就没有什么办法,所以要把分母变成“一个”。
分部积分
∫udv=uv−∫vdu
优先次序:对数、反三角(怕积分的)<多项式<指数、三角(求完还是它本身)。
分部积分凑微分
例如,我们看到 ∫xexdx,就要首先想到转换为 ∫xdex。
考虑数域 {eaxcosbx,eaxsinbx},其对求导与不定积分封闭,
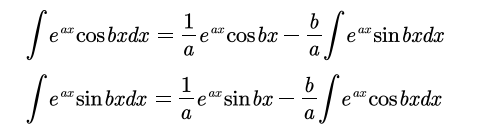
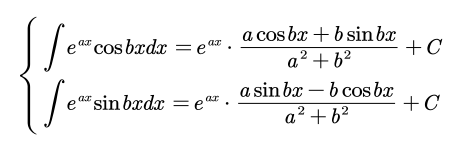
做题的时候,可以考虑 sinx,cosx 的共轭对,即对两个共轭的函数进行积分,得知互相的关系。凑微分的时候,可以放在一起凑。
事实上:
(P(x)cosbx+Q(x)sinbx)eax
都是封闭的,我们可以待定系数求解。
经常出现的形式:
ff′⇒lnf
1+f2f′⇒arctanf
1+x21⇒arctanx
−f′/f2⇒1/f
递推+分部积分

两种方法:第一类换元法,分部积分法,这里特别注意的是我们熟练运用 secx,tanx 的关系:
secx′=secxtanxtanx′=sec2xtan2x+1=sec2x
更进一步的,我们还可以求出:
∫sec5dx=sec3xtanx−∫tanxdsec3x=sec3xtanx−3∫tanxsecxtanxsec2xdx=sec3xtanx−3(∫sec5x−∫sec3x)
即可转化为上面的结果。
一些比较常规,经常出现的分部积分
求:
∫lnxdx=xlnx−∫xdlnx=xlnx−x+C
因此,任意底数 a 就除一个 lna 就行。
求:
∫ln(x+x2+a)dx=xln(x+x2+a)−∫x2+axdx=xln(x+x2+a)−x2+a
求:
∫arctanxdx
可以与上面类似的方法做出来,但是也可以令 x=tanθ,得:
∫θdtanθ=θtanθ−∫tanθdθ
一般一眼看上去全是反三角函数比较适合换元。
凑分部积分的方法
再次观察公式:
∫udv=uv−∫vdu
可以看到比较重要的是选择 dv 和选择好的 u 使得 du 比较简洁或者和 v 抵消。
凑 u
对 ln(sin/cos/tanx) 敏感,因为其求导之后三角函数的形式比较简洁。所以分部积分,我们尽量凑出
∫ln(...)dv
这就是巧妙选择了 u。
凑 v
分部积分法还有很重要的一点是 dv 的选取,尽量能够看出被积函数中长得像某个函数的导数的东西。
∫(x2−1)3xlnxdx
需要发现 d(−(x2−1)−21)……剩下的部分是倒置换。
一道比较相近的题:
∫(1+x2)23lnxdx
但是此时看到分子没有带 x,另寻别的换元的方法:
x=tant⇒∫lntantdsint
∫x(1+x)arctanxdx
2∫arctanxdarctanx=(arctanx)2+C
∫x2+1xtanx2+1dx

−f′(x)/f2(x) 形式
求
∫x21−lnxdx
这里需要使用代换 x21dx=d(−x1)。
这里,我们可以尝试着发现一些类似于 −f′(x)/f2(x) 和 f′(x)/f(x) 的部分,它们的原函数分别为 1/f(x) 和 ln∣f(x)∣。
计算反常积分:
∫0+∞(1+e−x)2xe−xdx
观察到这个等于:
∫0+∞xd1+e−x1
于是使用分部积分即可。
∫xarctanxln(1+x2)dx
我们联想到 arctanx,ln(1+x2) 求导之后都会产生一个 1+x2 的分母,于是凑出 d(1+x2),简便计算。其实本质上 x 是幂次好处理,于是凑出 1/2x2 再凑常数。
∫xexsinxdx
可以把 exsinx 凑微分,也可以观察到是 P(x)sinxex 的形式,待定系数法求解。
微分方程解出来是:
1
| [(1/2x)cos(1x)+(1/2x-1/2)sin(1x)]e^1x
|
∫e−sinxsin4(4π−2x)sin2x
分母降次,
用分部积分处理一些子式不存在初等函数作为原函数的被积函数,通过相减抵消掉不能积分的部分。
∫x2(x−1)exdx=∫xexdx+∫exd(1/x)=∫xexdx+xex−∫x1exdx=xex+C
当然有神仙一眼看出原函数……
∫arctanxdx
比较重要的是配凑常数,得到:
∫arctantd(t2+1)=(t2+1)arctant−t+C
是为了求导之后刚好能够凑出 1。
建立递推关系
求:
∫x2+a2dx
可以分部积分法,转化为处理:
∫x2+a2x2dx
这个的基本处理手段是拆分分子为 x2+a2−a2。
求:
∫secnxdx
∫tannxdx
建立递推关系:
Γ(x)=∫0∞tx−1e−tdt
Γ(x)=1/x∫0∞e−tdtx=Γ(x+1)/x
Γ(x+1)=xΓ(x)
是阶乘的推广。
建立递推关系:
an=∫01xlnnxdx
an=1/2∫01lnnxdx2=1/2x2lnx∣01−n/2∫01xlnn−1xdx=−2nan−1
计算:
∫(1+x−x1)ex+x1dx=xex+x1+C
分部积分求解:
设 f(x)∈C′[0,1],而且 f(0)=f(1)=0,求证:
(∫01xf(x)dx)2≤451∫01(f′(x))2dx
等号当且仅当 f(x)=A(x3−x) 时成立,其中 A 为常数。
我们需要用到柯西施瓦茨不等式,但是需要分离 f′(x) 出来,这就需要分部积分。
∫01xf(x)dx=∫01f(x)d(21x2+k)=∫01(21x2+k)f′(x)dx
这里用 k 是为了凑系数。
然后:
(∫01(21x2+k)f′(x)dx)2≤∫01(21x2+k)2dx∫01(f′(x))2dx
而:
∫01(21x2+k)2dx=∫01(41x4+x2k+k2)dx=201x5+31x3k+xk2∣01=k2+31k+201
极值就是 1/45,此时 k=−61。
柯西施瓦茨取等当且仅当 f′(x)=λ(21x2−61),就可以得到 f(x)=A(x3−x)+C,而 C=0 ,因为 f(0)=0。
欧拉换元法
ax2+bx+c=±(t−ax)=±(tx−c)=t(x−α)=(x−β)t
其中 α,β 是两根。核心是写成 mx+n 的形式。同时让 x 的表达式不太过复杂。s
有理函数积分
常规方法
∫x2+px+q1dx
凑成 ∫u2±a2du。
∫x2+px+qxdx
凑分母导数:2x+p。
∫x2+px+qx2dx
首先分子降次,转化为前两种情况。
技巧
有几种非常重要的方法:
- 待定系数法(最为常规)。
- 凑“假分式”,即对分子进行拆分。
- 倒置换,一般分母比较大。
- 换元 x±x1,一般出现在分子的最高次数是 2,分母的最高次数是 4 时,上下同除 x2。
求:
∫x(x10+1)dx
可以使用凑微分法,碰到 x 在分母和次数特别高的其他项 xkr,就要上下同乘 xr−1。
可以使用凑假分式法,
∫x(x10+1)1+x10−x10dx=ln∣x∣−101ln(x10+1)+C
求:
∫x8(1+x2)1dx
可以倒置换。
也可以拆项:
∫x8(1+x2)1−x8+x8dx=∫(1−x2+x4−x6)/x8+1+x21dx
组合积分
求:
∫x4+1dx,∫x4+1x2dx
构造一对积分:
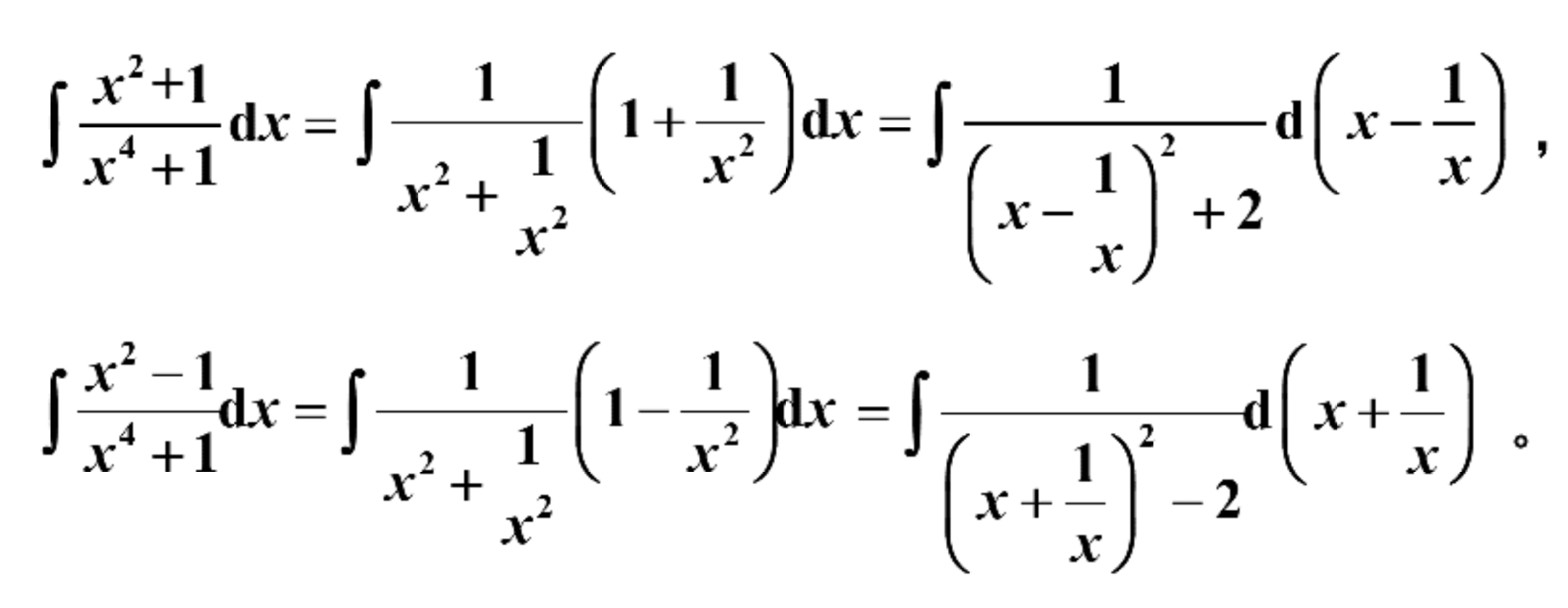
21arctan2x−x1+C
−21221ln∣∣∣∣∣(x+x1)2−2(x+x1)2−2∣∣∣∣∣
也可以配方法:
∫(x2+2x+1)(x2−2x+1)1dx
另外,比较好求的是:
∫1+x4xdx=21arctan(x2)+C
∫1+x4x3dx=41∫1+x4dx4=41ln(1+x4)+C
求
∫x+3x1dx
代换的时候,特别注意 x=x21,3x=x31,两者取“公因数” x61,于是应该这样换元……
求
∫x4+x61dx
主要问题是如何分解,注意到分母分解为 x4(x2+1),然后乘一个 (x2−1),就可以进行裂项……
求
∫x6+11dx
拆分:
∫1−x2+x41dx−31∫x6+1dx3
再处理左边的,拆分:
∫1−x2+x41+x2dx,∫1−x2+x41−x2dx
求
∫1+x61+x4dx
(1+x6)=(x2+1)(x4−x2+1)。凑出来 x4−1+2,就可以转化为上面的积分。
三角函数有理式
∫R(sinx)cosxdx/∫R(cosx)sinxdx
第一类换元法
∫R(sin2x,sinxcosx,cos2x)dx
令 tanx=u,则 du=sec2xdx,将 dx=sec2xdu 代回原式。然后全部转化为 secx,tanx 的式子,最后运用 tan2x+1=sec2x 即可。
- sin2x=tan2x+1tan2x。
- cos2x=1+tan2x1。
- sinxcosx=sin2xcos2x=1+tan2xtanx。
- dx=(1+tan2u)du。
求:
∫(3sinx+2cosx)21dx
积化和差
降幂
无分数:降幂,有分数:凑 dtanx,奇数次幂:凑不同三角函数。优先统一角度。
∫sin4xcos2xdx
降幂的公式:
sinxcosx=21sin2xcos2x=21(cos2x+1)
∫5(2x+sin2x)cos2xdx
基本方法:多次降幂即可。本质是化归的思想,P(x)sinx 我们会积,sinax,cosbx我们也会积,就要转化为这样的形式。
凑微分方法:cos2x=21+cos2x=(2x+sin2x)′/4。
万能代换
t=tan2x:
sinx=1+t22t,cosx=1+t21−t2,dx=1+t22dt

通常使用:分母三角函数幂次低。无法丢掉分母常数的时候只能用万能公式。
共轭组
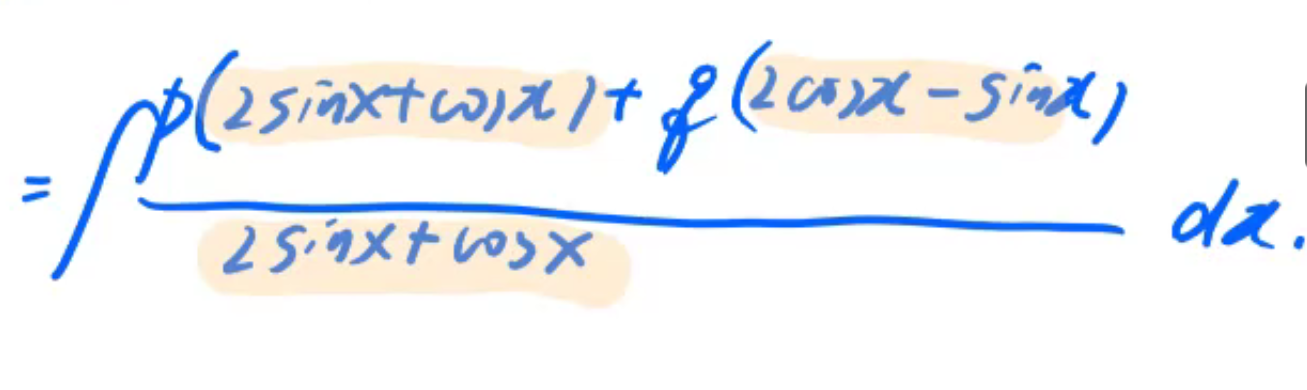
px+qln(2sinx+cosx)+C
分母处理
- /(sinx−1),上下同乘 sinx+1,然后进行拆分。
- /(cosx+1),转化为 2cos22x。
- /(sinx±cosx) 辅助角公式。
无理函数积分
一般思想是替换根号内的数,采用第二换元法。
例如:
∫x231−xdx
∫tanxdx
令 t=tanx,x=arctan(t2)。
∫t1+t412tdt=2∫1+t4t2dt
∫01x(1−x4)3dx
换元 x2=sint,可以转化为
21∫02πcos3tcostdt
不能用初等函数表示出的积分
∫x+Asinxdx,∫x+Bcosxdx,∫e±x2dx,∫lnx1dx,∫esinx/cosxdx,∫sinx2dx