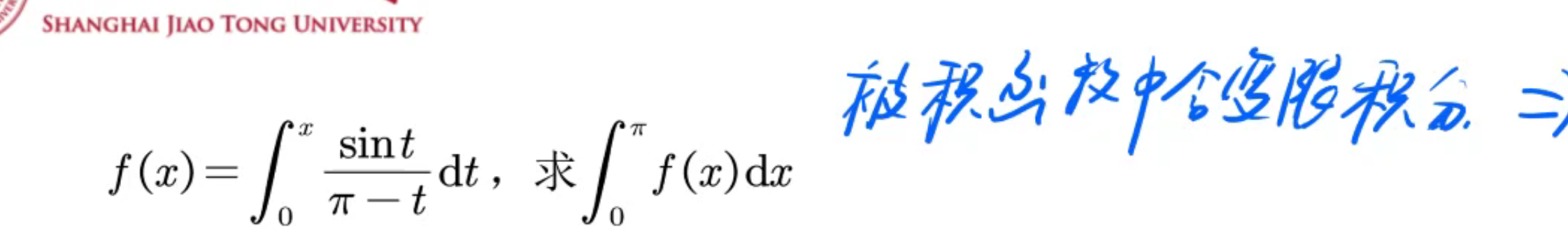定积分 new

换元法：注意改变积分的上下限。

分部积分法。

不一样的是，定积分对变量的范围做出了限制，而不定积分只要对任意一个小区间都成立即可。所以，需要关注：

• 定义域，值域，例如三角函数加绝对值等。
• 一些特有的性质，例如奇偶性、周期性。

证明：

$\int_a^{a+T} f(x)\mathrm d x=\int_0^T f(x) \mathrm d x$

换元法，令 $t=x-a$，左式转换为 $\int _0^{T} f(t+T)\mathrm d t=\int _0^T f(x)\mathrm d x$。我们可以主动地运用换元法，来调整积分的上下限。

证明：

$\int _a^b f(x) \mathrm d x=\int _a^b f(a+b-x) \mathrm d x$

也是换元，令 $t=a+b-x$，注意交换积分上下限。

如果函数具有某种对称性，我们可以转化为计算：

$\frac{1}{2} (\int _a^b f(x)\mathrm d x+\int _a^b f(a+b-x)\mathrm d x)$

特别地，当 $b=-a$……

任意一个函数都可以拆分为一个奇函数和一个偶函数的和，只需：

$f(x)=\frac{F(x)-F(-x)}{2} ,g(x) = \frac{F(x)+F(-x)}{2},F(x)=f(x)+g(x)$

于是 $\int_{-a}^a F(x) \mathrm d x=2\int _0^a g(x)\mathrm d x$。更多的情况，我们需要自己发现函数中存在的奇函数与偶函数，例如：

$\int _{-1}^1 [x^2(1-x^2)^\frac{1}{2}+x^3\cos x]\mathrm dx$

可以转化为：

$2 \int _0^1 x^2(1-x^2)^\frac{1}{2}\mathrm d x$

三角换元之后用 Wallis 公式。（于是我们希望三角函数幂次尽量高）

证明：

$\int_0^\frac{\pi}{2} f(\sin x,\cos x)\mathrm d x=\int _0^\frac{\pi}{2} f(\cos x,\sin x)\mathrm d x$

因为 $\sin x=\cos \frac{\pi}{2}-x$。

$\int _0^\pi f(\sin x)\mathrm d x=2\int _0^\frac{\pi}{2} f(\sin x)\mathrm d x$

$\int _0^\pi xf(\sin x)\mathrm d x=\frac{\pi}{2} \int_0^\pi f(\sin x)\mathrm d x$

构造函数 $(x-\frac{\pi}{2}) f(\sin x)$，左边关于 $(\pi/2,0)$ 中心对称，类比奇函数，右边关于 $x=\pi/2$ 对称，类比偶函数。

更进一步，对于任意的关于 $(\pi/2,0)$ 中心对称的函数 $g(x)$，都有 $\int _0^\pi g(x)f(\sin x)\mathrm d x=0$。

求定积分：

$\int _0^2 (2x+1)\sqrt{2x-x^2}\mathrm d x$

左边转化为 $(2(x-1)+3)$，可以把原来的函数转化为中心对称乘轴对称加上另外一个函数。

因此，我们需要时刻关注函数对积分中点的对称性。

求：

$\int_0^\frac{\pi}{2} \frac{\mathrm d x}{1+\tan x}$

利用对偶式，两个相同的值加起来等于 $\pi/2$。

求：

$I=\int_0^\frac{\pi}{2} \ln\sin x\mathrm d x$

利用区间再现：

$\frac{1}{2} \int_0^\frac{\pi}{2} \ln\sin x\cos x\mathrm d x=\frac{1}{2}\int_0^\frac{\pi}{4}(\ln\sin2x - \ln2 )\mathrm d 2x=\frac{1}{2} I-\frac{\pi}{4}\ln2$

$I=-\frac{\pi}{2}\ln2$

区间在线公式：经常有 $\ln(e^x+1),\ln(\tan x+1)$ 等等，如：

$\int_0^1 \frac{\ln(x+1)}{x^2+1}\mathrm d x$

$ t= \arctan x$，则：

$1/2\int _0^\frac{\pi}{4} \ln (\tan t+1)(\tan (\frac{\pi}{4}-t)+1) \mathrm d t$

设函数 $f(x) \in C[-1,1]$，且对于 $[-1,1]$ 上的任意偶连续函数 $g(x)$，都有 $\int _{-1}^1 f(x)g(x) \mathrm d x=0$，试证明 $f(x)$ 是 $[-1,1]$ 上的奇函数。

$\int _{-1}^1 f(x)g(x) \mathrm d x=\int _{-1}^1 f(-x)g(-x) \mathrm d x=\int _{-1}^1 f(-x)g(x) \mathrm d x$

因此：

$\int _{-1}^1 (f(x)+f(-x))g(x) \mathrm d x \equiv 0$

我们想要证明 $f(x)+f(-x)\equiv 0$，回想积分证明某一个函数恒等于 $0$，只要 $\varphi(x)\ge 0$，且 $\int_a^b \varphi(x)=0$，就可以证明 $\varphi (x)\equiv 0$。

所以我们这里取 $g(x)=f(x)+f(-x)$ 是一个偶函数，得到 $\int _{-1}^{1} (f(x)+f(-x))^2 \mathrm dx=0$，即可以证明。

更进一步，对于任意 $g$ 都有 $\int fg\mathrm d x=0$，就知道 $f\equiv 0$。

我们也可以把 $f(x)$ 分解为 $\alpha(x)=(f(x)-f(-x))/2,\beta(x)=(f(x)+f(-x))/2$，原条件转化为 $\int \beta(x)g(x)\mathrm d x\equiv 0$。

抽象函数的分部积分提高导函数阶数。

假设 $w'=v$

$\int u\mathrm d v=uv-\int u'\mathrm d w=uv-(u'w-\int w\mathrm d u')$

这样可以看出来是逐步提高求导阶数。

已知 $g(x)=\int _0^x f(t)\mathrm d t$，$\int _0^\frac{\pi}{2} f'(x)\sin x\mathrm d x=2$，且 $f(\pi/2)=3$，求：

$\int _0^\frac{\pi}{2} g(x)\sin x \mathrm d x$

已知相当于 $\int _0^\frac{\pi}{2}g''(x)\sin x \mathrm d x$，存在高阶导数，那么可以考虑多次分部积分。

$-\int_0^\frac{\pi}{2} g(x)\mathrm d \cos x\\=-g(x)\cos x|^\frac{\pi}{2}_0+\int_0^\frac{\pi}{2} \cos x\mathrm d g(x)\\=(\underline{-g(x)\cos x|^\frac{\pi}{2}_0}=0) +\sin x g'(x)|^\frac{\pi}{2}_0-\int _0^\frac{\pi}{2} \sin x\mathrm dg'(x)\\=3-2=1$

若函数 $f(x)$ 是偶函数，则 $\int _0^x f(t)\mathrm d t$ 是奇函数。平常这个不应该成立，但是这里过原点。

若函数 $f(x)$ 是奇函数，则 $\int_0^x f(t)\mathrm d t$ 是偶函数。

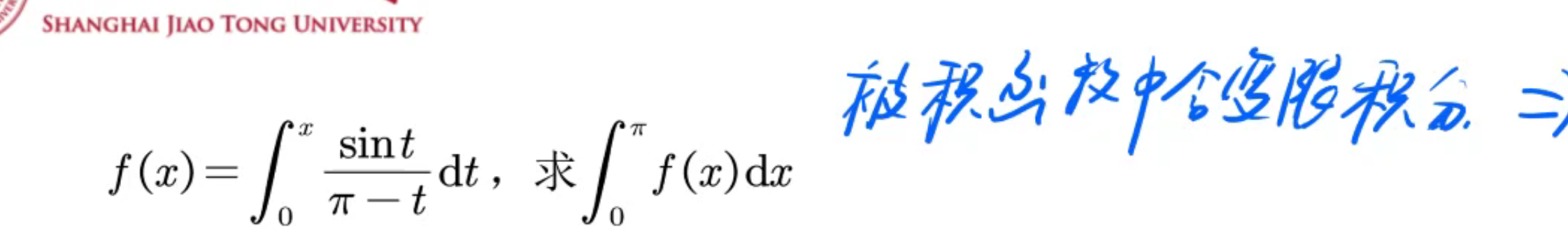
分部积分。

$\int_0^\pi f(x)\mathrm d (x-\pi)=0-\int_0^\pi \sin x\mathrm d x$

否则积不出来。

Euler 积分

$\int _0^\frac{\pi}{2} \ln\sin x\mathrm d x$

$\frac{1}{2}\int_0^\frac{\pi}{2} \ln\frac{1}{2}\sin 2x \mathrm d x=\frac{1}{4}\int_0^\frac{\pi}{2} \ln\sin 2x\mathrm d 2x-\frac{1}{2}\ln2\frac{\pi}{2}=\frac{1}{2}\int_0^\frac{\pi}{2}\ln\sin t \mathrm d t-\frac{\pi}{4}\ln 2$

$I=-\frac{\pi}{2}\ln2$

定量计算定积分误差

主要利用好拉格朗日中值定理、积分中值定理以及定积分的定义。

设 $A_n=\frac{n}{n^2+1}+\cdots+\frac{n}{n^2+n^2}$，求 $\lim_{n \to +\infty} n(\frac{\pi}{4}-A_n)$。

先表示 $\frac{\pi}{4} -A_n$，令 $f(x)=\frac{1}{1+x^2}$

$\frac{\pi}{4}-A_n=\int_0^1\frac{\mathrm dx}{1+x^2}-A_n=\sum_{i=1}^n \int_{\frac{i-1}{n}}^\frac{i}{n}f(x)-\frac{n^2}{n^2+i^2} \mathrm d x(对定积分进行了拆分)$

$=\sum_{i=1}^n \int _{\frac{i-1}{n}}^\frac{i}{n} f'(\xi_i)(x-\frac{i}{n}) \mathrm d x(使用拉格朗日中值，其中 \xi_i \in [\frac{i-1}{n},\frac{i}{n}])$

$=\sum_{i=1}^n f'(\eta_i) \int_\frac{i-1}{n}^\frac{i}{n} (x-\frac{i}{n})\mathrm d x(使用积分中值，要利用 f'(\eta_i) 在 f'(x),x\in[\frac{i-1}{n},\frac{i}{n}] 值域内)$

$\sum_{i=1}^n (-\frac{f'(\eta_i)}{2n^2})$

然后乘以 $n$，利用积分的定义，得到答案是 $\frac{1}{4}$。

设函数 $f(x)$ 在闭区间 $[0,1]$ 上具有连续导数，且 $f(0)=0$，$f(1)=1$，证明：

$\lim_{n \to \infty} n(\int_0^1 f(x)\mathrm d x-\frac{1}{n}\sum_{k=1}^n f(\frac{k}{n}))=-\frac{1}{2}$

$\int_0^1 f(x)\mathrm d x-\frac{1}{n}\sum_{k=1}^n f(\frac{k}{n})=\sum_{k=1}^n \int _\frac{k-1}{n}^\frac{k}{n}f(x)-f(\frac{k}{n})\mathrm d x$

$=\sum_{k=1}^n \int_\frac{k-1}{n}^\frac{k}{n} f'(\xi_i)(x-\frac{k}{n})=\sum_{k=1}^nf'(\eta_k) \int_\frac{k-1}{n}^\frac{k}{n}(x-\frac{k}{n})\mathrm d x$

$\sum_{k=1}^n f'(\eta_k)(-\frac{1}{2n^2})$

原式转化为：

$\lim_{n \to +\infty} -\frac{1}{2}\sum_{k=1}^n f'(\eta_k) \frac{1}{n}=-\frac{1}{2}(f(1)-f(0))=-\frac{1}{2}$