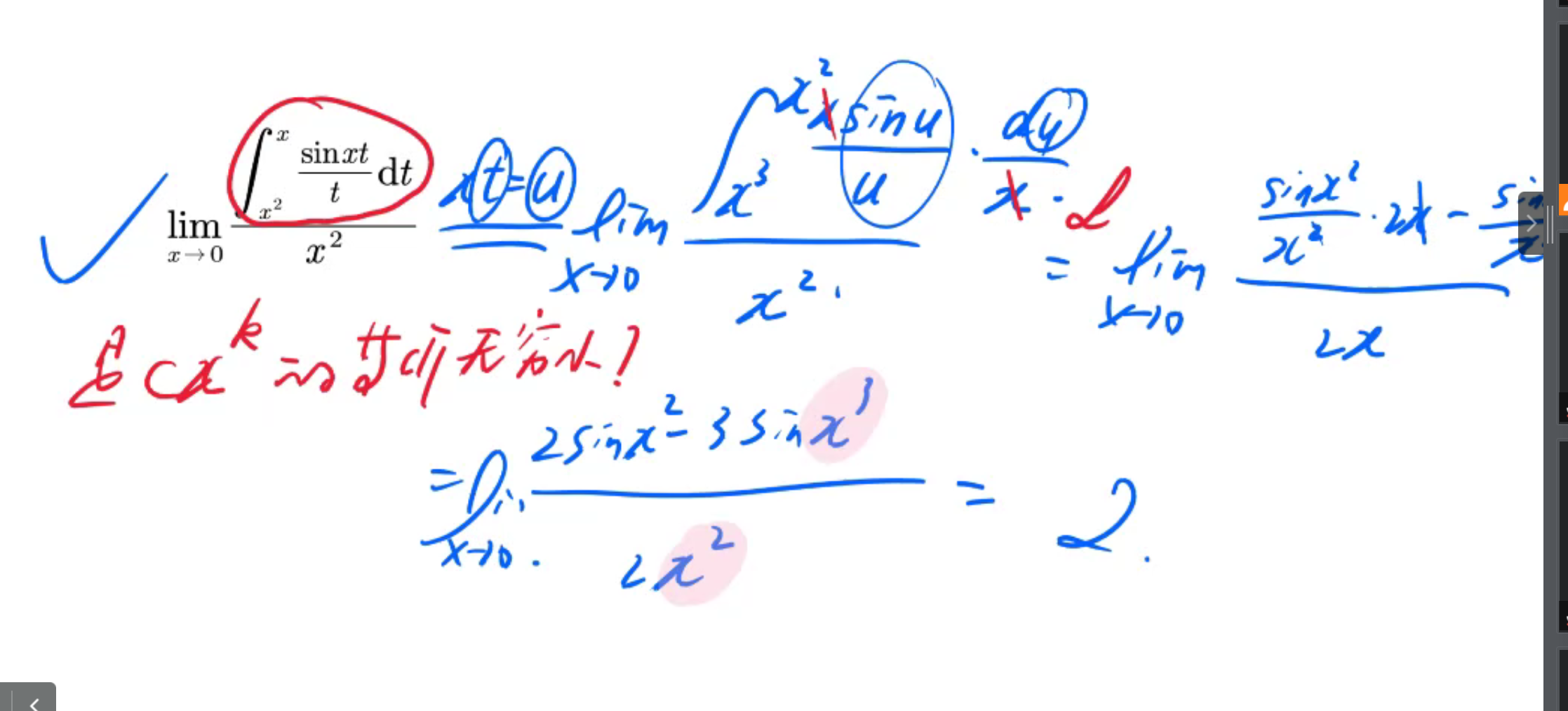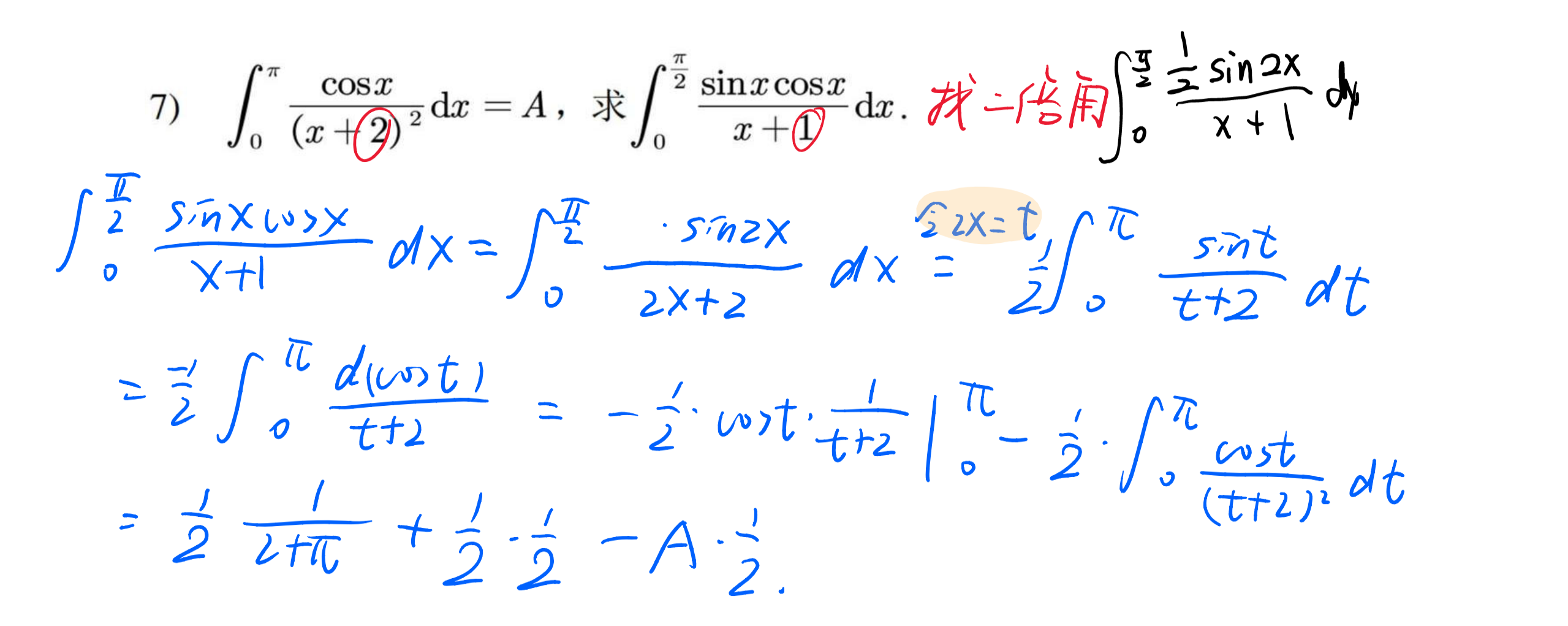抽象函数的定积分

变量代换的技巧

第一是观察函数的结构，比如出现 $f(x^2)$ 则令 $u=x^2$。

第二是观察积分的上下限，比如出现 \int_0^\sqrt{T}，则令 $u=x^2$。

求：

$\lim_{x \to 0} \frac{\int_0^x t f(x^2-t^2)\mathrm d t}{x^4}$

令 $u=x^2-t^2$，是为了转化为变上限积分的结构。

$-\frac{1}{2}\lim_{x\to 0} \frac{\int_{x^2}^{0} f(u)\mathrm d u}{x^4} = \frac{1}{4} \lim_{x \to 0} \frac{f(x^2)}{x^2}=\frac{1}{4}f'(0)$

还是用一次洛必达之后使用定义。还要记得变上限积分求导要求被积函数没有与 $x$ 相关的量。

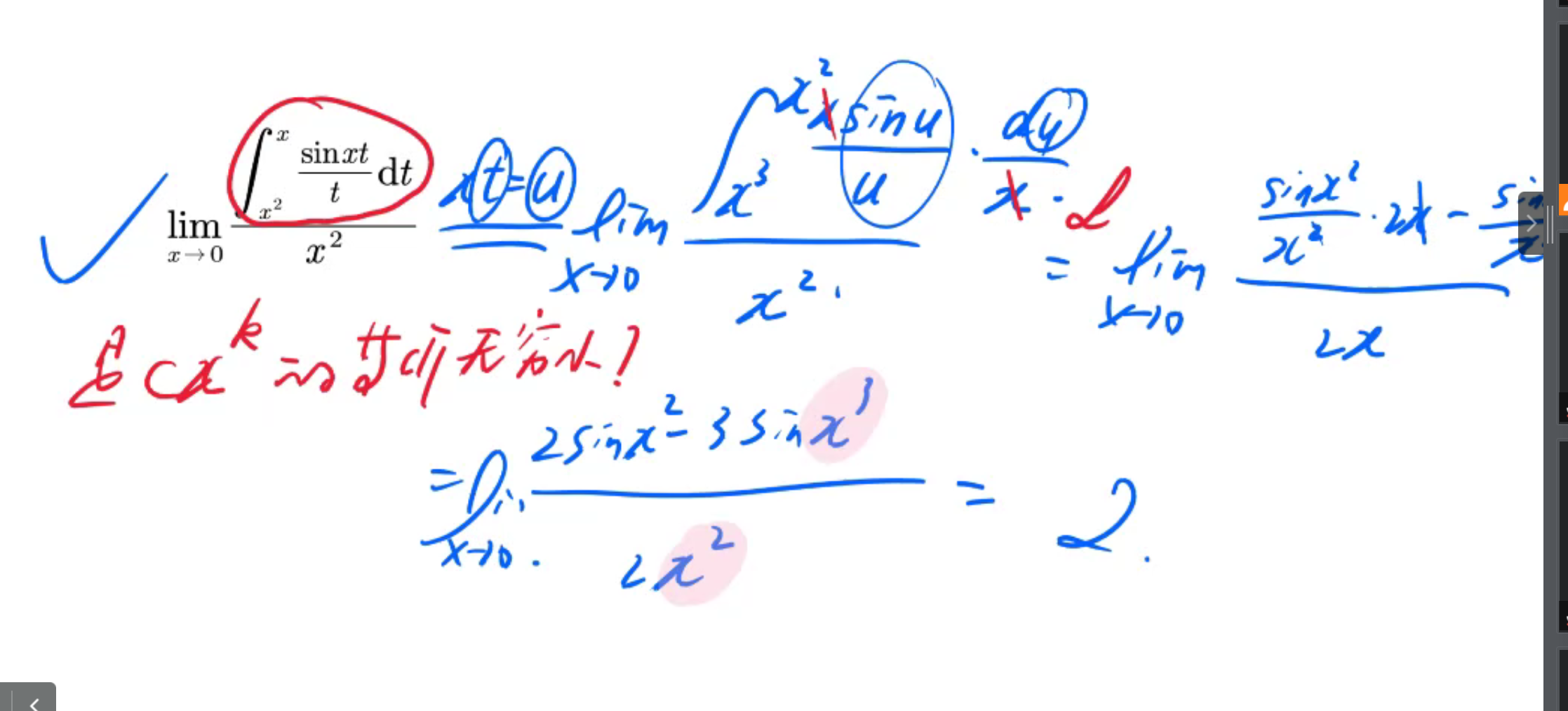
若常数 $c<2$，则存在一个定义在 $[0,1]$ 上的非负连续函数 $f(x)$，使得 $\int_0^1 f(x)\mathrm d x=1$，但 $\int_0^1 f(\sqrt{x})\mathrm d x>c$。

考虑 $f(x)=nx^{n-1}$，则 $\int _0^1 f(x)\mathrm d x=x^n|^1_0=1$。

$\int_0^1 u f(u) \mathrm d u > c/2$

$\int_0^1 nu^{n}\mathrm d u=\frac{n}{n+1}u^{n+1}|^1_0=\frac{n}{n+1}$

就令 $n=[\frac{2}{2-c}]+1$ 就行了。

证明：

$\int_0^1 \frac{\cos x}{\sqrt{1-x^2}}\mathrm d x > \int_0^1 \frac{\sin x}{\sqrt{1-x^2}}\mathrm d x$

$\int _0^2 f(x)\mathrm d x=4,f(2)=1,f'(2)=0,\int_0^1 x^2f''(2x)\mathrm d x=?$

逐渐分部提高阶数。

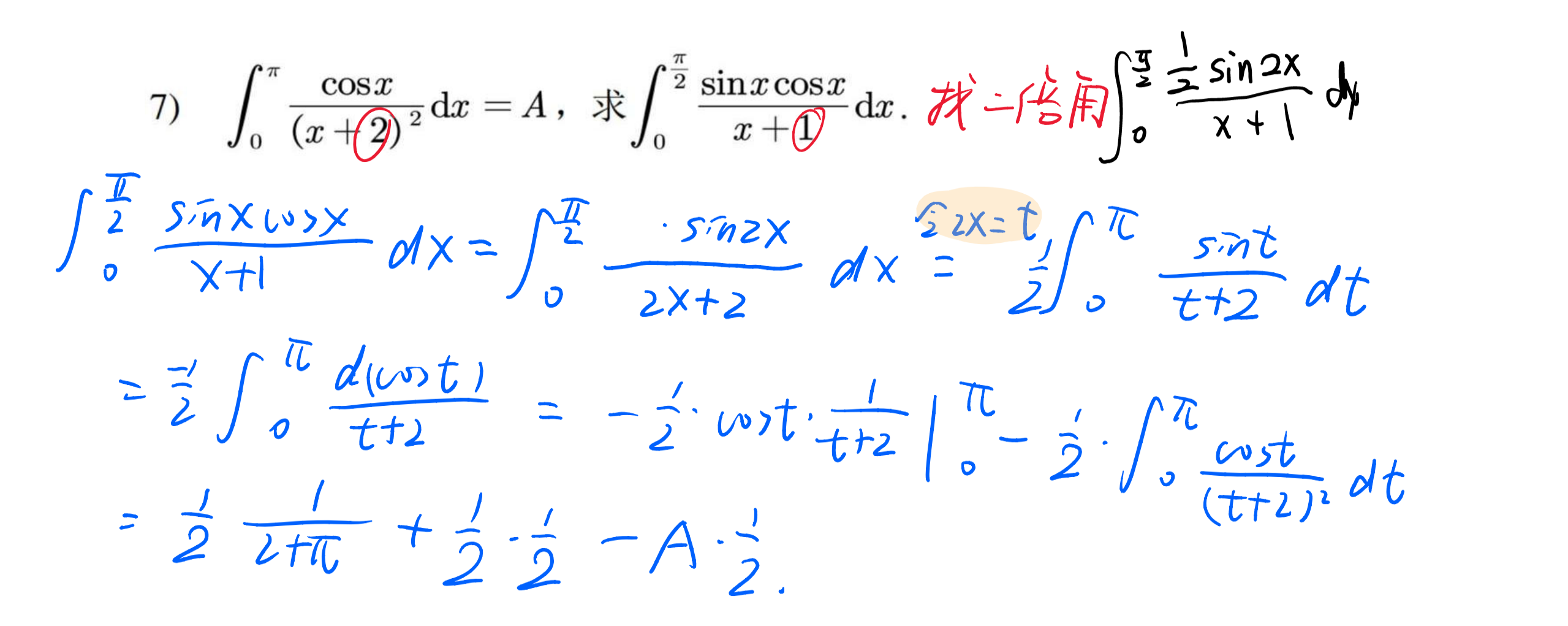
分部积分

为了提升导函数的阶数。也可以考虑泰勒公式。

$f'(x) \in C[0,2\pi]$，且 $f'(x)\ge0$，证明，对于 $\forall n$，

$|\int _0^{2\pi} f(x)\sin nx\mathrm d x| \le \frac{2[f(2\pi)-f(0)]}{n}$

条件给到导函数上，为了构造出导函数，写成

$-\frac{1}{n}\int_0^{2\pi} f(x) \mathrm d \cos nx = -\frac{1}{n}(f(x)\cos nx | _{0}^{2\pi} -\int_0^{2\pi} \cos nx f'(x)\mathrm d x)$

再利用 $|\cos nx|\le 1$ 放缩即可。

设 $f(x)$ 和 $g(x)$ 在 $[0,b]$ 上具有非负连续的导函数，且 $f(0)=0$，试证：

对于 $0<a\le b$，有：

$f(a)g(b)\le\int_0^a g(x)f'(x)\mathrm d x +\int_0^b f(x)g'(x)\mathrm d x$

$\begin{aligned} \int_0^a g(x)f'(x)\mathrm d x +\int_0^b f(x)g'(x)\mathrm d x &= g(x)f(x)|^a_0 -\int_0^a g'(x)f(x)\mathrm d x+\int_0^b f(x)g'(x)\mathrm d x \\ &=g(a)f(a)+\int_a^b f(x)g'(x)\mathrm d x \\ ans-RHS&=(g(a)-g(b))f(a)+\int_a^b f(x)g'(x)\mathrm d x \end{aligned}$

可以根据广义积分中值定理：

$(g(a)-g(b))f(a)+f(\xi)\int_a^b g'(x)\mathrm d x$

等于：

$(g(a)-g(b))(f(\xi)-f(a))$

$a_n=\int_{n}^{n^2} \frac{\sin \pi x}{x^2}\mathrm d x$，其中 $n$ 是正整数，证明：

1. $0<a_{2n}<\frac{1}{2n}$。

右边直接把 $\sin \pi x$ 放成 $1$，得到小于等于 $\frac{1}{2n}-\frac{1}{4n^2}$。

左边可以发现 $x \in [2k+1,2k+2]$ 的区间中整体积分式小于 $0$ 的，于是要证明积分总体大于 $0$，只需证明相邻的区间之和是 $>0$ 即可。

2. 当 $n \to +\infty$ ，$a_n=o(\frac{1}{n})$。

利用分部积分。常数可以不管

$a_n= -\frac{1}{\pi}\int_n^{n^2}\frac{\mathrm d \cos \pi x}{x^2} = \frac{\cos \pi x}{x^2}|_n^{n^2}-\int_n^{n^2} \cos \pi x\frac{\mathrm d x}{x^3}$

这个能看出是低于 $1/n$ 的。

泰勒公式

设 $a>0$，函数 $f(x)$ 在闭区间 $[-a,a]$ 上有二阶连续导数，证明：

$\exists \xi \in [-a,a],s.t. \int_{-a}^a f(x)\mathrm d x=2af(0)+\frac{1}{3}a^3 f''(\xi)$

第一是展开后积分，$f(x)=f(0)+f'(0)x+\frac{f''(\xi)}{2} x^2$。

$\int_{-a}^a f(x)\mathrm dx = \int_{-a}^a f(0) \mathrm d x+\int_{-a}^a f'(0)x \mathrm d x+\int_{-a}^a \frac{f''(\xi)}{2} x^2 \mathrm d x$

$=2(af(0)+\frac{1}{6} a^3 f''(\xi))$

注：$x^{2k-1}$ 由于是奇函数于是会被抵消，$x^{2k}$ 是对称的，于是就可以只算一遍。

证明有两个零点的常用方法：配凑保号函数

设 $f(x) \in C[a,b]$，且 $\int_a^b f(x) \mathrm d x=0,\int_a^b xf(x) \mathrm dx=0$，求证 $(a,b)$ 中至少存在两个不同点 $x_1,x_2$，使得 $f(x_1)=f(x_2)=0$。

第一个点可以用积分中值定理，得 $f(x_1)(b-a)=0$，$x_1 \in (a,b)$，第二个点 $x_2$ 不太好处理，我们证明如果只存在唯一零点，那么矛盾，假设只存在 $x_1$ 一个零点，根据 $f(x) \in C[a,b]$，$(x-x_1)f(x)$ 是保号的（$\le 0$ 或 $\ge 0$），而 $\int_a^b (x-x_1)f(x)=\int_a^b xf(x)-x_1\int_a^b f(x)=0$，那么只能 $(x-x_1)f(x) \equiv 0$，与唯一零点矛盾，于是还存在 $x_2$ 一个零点。

设 $f(x) \in C[0,\frac{\pi}{2}]$，且：

$\int_0^\frac{\pi}{2} f(x)\sin x \mathrm d x=\int _0^\frac{\pi}{2} f(x)\cos x \mathrm d x=0$

证明：$f(x)$ 在 $(0,\frac{\pi}{2})$ 至少存在两个零点。

首先发现 $\sin x$ 在 $(0,\frac{\pi}{2})$ 是保号的，由积分中值定理，$\exists x_1 ,s.t. f(x_1) \int _0^\frac{\pi}{2} \sin x\mathrm d x=0$ ，则 $x_1$ 是 $f(x)$ 的零点。

之后，假设只存在 $x_1$ 一个零点，$f(x)$ 在 $x_1$ 两侧异号，想到继续构造一个保号函数，$\int_0^\frac{\pi}{2} f(x) \sin(x-x_1) \mathrm d x$，可以由两个积分组合而来，恒等于 $0$，这就说明 $f(x)\equiv 0$，与 $x_1$ 一个零点矛盾。

积分不等式

证明：

$\int_a^b |f(x)|\mathrm d x \le \frac{(b-a)^2}{2} \max_{x \in [a,b]} |f'(x)|$

利用拉格朗日公式对函数的约束。这样是约束在一个平行四边形中。如果用泰勒公式 $f(x) = f(a)+(x-a)f'(a)+\frac{f''(\xi)}{2}(x-a)^2$，也可以约束在一个抛物线的边构成的图形之中，以此类推，事实上，凸函数可以看做约束在 $f(a)+(x-a)f'(a)$ 的上/下。