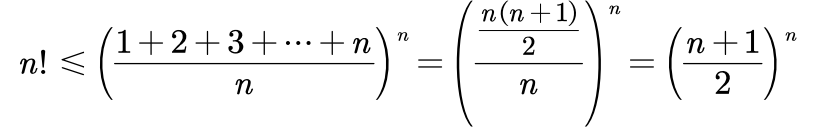不等式与最值

不等式法

基本：均值不等式、柯西不等式。

均值不等式建立了变量的和与积之间的关系，柯西不等式建立了平方和与一次式之间的大小关系，也可以处理分式表达式的分母。

高数第一章讲的 $A-G$ 不等式：

A(average)=\frac{x_1+x_2+\cdots+x_n}{n}\\ G(geometry)=\sqrt[n]{x_1x_2\cdots x_n}\\ G\le A

$A-G$ 不等式的证明可以使用数学归纳法：

这里假设最大正数是 $x_{k+1}$ ，是为了 $\frac{x_{k+1}-A_k}{k+1}$ 是一个正数，从而使得二项式展开中的不等式成立。对于二项式展开，我们在后面也经常使用它的推论伯努利定理以及其变种，获得一系列不等式。

利用 $A-G$ 不等式，我们容易得到以下推论。

下面我们来看一道比较有技术含量的题目。

证明：

\sqrt[n]{n}-1<\frac{2}{\sqrt{n}},n\in \mathbb{N}_{+}

首先，我们观察到当 $n \to +\infty$ ，显然 $\sqrt[n]{n} \to 1$ ，更加具体地， $\ln \sqrt[n]{n}=\frac{1}{n} \ln n$ ，当 $n=e$ 有极大值， $n \to +\infty$ ，它的值 $\to 0$ 。

这样，我们就发现 $\sqrt[n]{n}-1$ 是一个小量。

至于小量的估计，我们采用二项式展开，比较精准，可以类比中学我们算 $(1+0.01)^{10}$ 之类的，展开到两三项之后精度就够了。

这样，我们令 $\sqrt[n]{n}-1=a$ ，则 $n=(1+a)^n=1+na+\frac{n(n-1)}{2} a^2 + \cdots \ge 1+\frac{n(n-1)}{2}a^2$ ，推出：

a<\frac{\sqrt{2}}{\sqrt{n}}<\frac{2}{\sqrt{n}}

这里吐槽以下舍去了 $na$ 这一项就有点草率了，但是本身不等式就比较宽。

我们还有另外一个方法，令 $\sqrt[n]{n}=t$ 注意到 $n-1=(t -1)(1+t+t^2+\cdots+t^{n-1})$ ，这样我们就可以利用类似以上的推论。

t-1=\frac{n-1}{1+t+t^2+\cdots t^{n-1}}\le\frac{n-1}{n\sqrt[n]{t^{n(n-1)/2}}}=\frac{n-1}{n\sqrt[n]{n^{(n-1)/2}}}<\frac{n^{\frac{1}{2n}}}{\sqrt{n}} \le \frac{2}{\sqrt{n}}

当然上述对 $n \ge 3$ 才成立，但不难验证结论对 $n=1,2$ 成立，估计是因为 $n \ge e$ ， $\sqrt[n]{n}$ 单减，才会出现这样的分界。

接下来我们看 $A-G$ 不等式在一些自主招生题目中的运用。

2018 北大

x+y=1,(\frac{1}{x}+\frac{27}{y^3})_{\min}=?

寻求 $x,y$ 与 $\frac{1}{x},\frac{27}{y^3}$ 之间的关系。

x+\frac{1}{x} \ge 2\\ \frac{y}{3}+\frac{y}{3}+\frac{y}{3}+\frac{27}{y^3} \ge 4\sqrt[4]{\frac{y}{3}\times\frac{y}{3}\times\frac{y}{3}\times\frac{27}{y^3}}=4

例题：

x+y+z=1\\ (x^2yz+xyz^2)_{\max}=?

x^2yz+xyz^2=y \times xz(x+z)=(1-x-z)xz(x+z) \cdots\\ \text{or} \\ 2y \times x \times z \times (x+z) \le ... 无法取等\\ \frac{1}{12}(2x)(3y)(2z)(x+z) \le \frac{1}{12}(\frac{3x+3y+3z}{4})^4 可以取等！

例题：

(x^2yz+2xyz^2)_{\max}=?

xyz(x+2z)=\frac{1}{abc} (ax)(by)(cz)(x+2z) \le \frac{1}{abc}[\frac{(a+1)x+by+(c+2)z}{4}]^4

首先确保 $a+1=b=c+2$ ，其次是 $ax=by=cz=x+2z$ 有解，最后别忘记 $x+y+z=1$ 。

这就需要我们检验取等条件，如果取不到还要待定系数……

求导

核心是主元法。还可以求偏导、运用线性规划，转化为几何意义，如切线、切点、斜率、面积、截距等。

$f_1(x,y,z,\cdots)=0,f_2(x,y,z,\cdots)=0,\cdots,g(x,y,z,\cdots)_{\max}=?$ 。

构造：

\Phi(x,y,z,\cdots)=\lambda f_1(x,y,z,\cdots)+\mu f_2(x,y,z,\cdots)\cdots+g(x,y,z\cdots)

联立方程

\frac{\partial \Phi}{\partial x}=\frac{\partial \Phi}{\partial y}=\frac{\partial \Phi}{\partial z}=\cdots=0\\ f_1(x,y,z,\cdots)=0\\ f_2(x,y,z,\cdots)=0\\ \cdots

f(A,B,C)=\sin A+\sin B\sin C\\ f(A,B,C) \le f(A,\frac{B+C}{2},\frac{B+C}{2})\\ \Leftrightarrow \sin B\sin C \le \frac{1-\cos(B+C)}{2} \Leftrightarrow \cos(B-C) \le 1

然后带入 $\frac{B+C}{2}=\frac{\pi-A}{2}$ 。其实观察到 $B,C$ 对称，可以猜 $B=C$ 。

调整的方向：往取等条件去靠，注意要满足题目的限制。

a^2+b^2+c^2=1\\ a=\cos\theta\\ b=\sin\theta\cos\varphi\\ c=\sin\theta\sin\varphi