高数第二弹 函数

函数

函数的概念

例题

开区间 $(0,1)$ 与闭区间 $[0,1]$ 之间存在双射。

例如：

$f(x)= \left\{ \begin{aligned} &x,x\not=\frac{1}{2^n},n \in \mathbb{N}\\ &0, x=\frac{1}{2},x \in(0,1)\\ &\frac{1}{2^{n-2}},x=\frac{1}{2^n}(n\ge 2) \end{aligned} \right.$

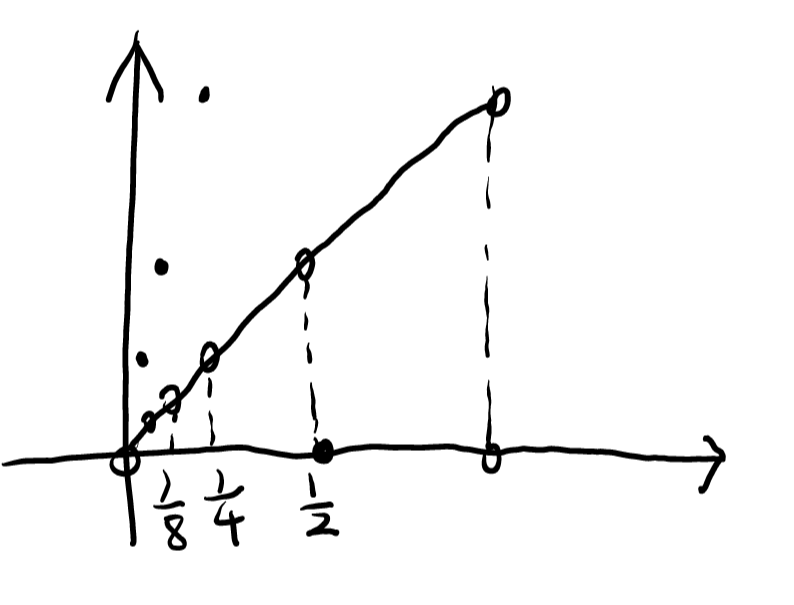
我们思考这个构造的意义，其实是利用了函数 $\frac{1}{2^n}$ 的性质，它收敛于 $0$，也就是我们有无限的 $\frac{1}{2^n}$ 使其处于 $(0,1)$，我们开了两个坑，把 $\frac{1}{4},\frac{1}{2}$ 上的值设成了 $1,0$，为了填回这个坑，我们就需要让 $f(\frac{1}{8})=\frac{1}{2}$ 对应的原来的值 $=\frac{1}{2}$。然后 $f(\frac{1}{16})$，$f(\frac{1}{32})$ 等等也需要填，等于是进入一个无限填坑的状态(？)，然而我们手下的 $\frac{1}{2^n}$ 是无限的，于是这样看来所有的坑都应该是被填完的。

我们还可以推广这个结论，得到任意一个区间 $A$ 和另一个区间 $A\cup\{x_1\}\cup\{x_2\}\cup\cdots$ 都存在双射。

函数方程

可以关注一下括号内的表达式成周期的情况，如 $f(x)\cdots=f(\frac{x}{x-1})\cdots$ 的情况。

函数的简单性质

例题

设函数 $f(x)$ 是定义在 $(-\infty,+\infty)$ 上的周期函数，并且有周期 $T>0$，证明：

若对于任意的 $x\in(0,T)$，有 $f(x) \not=f(0)$，则 $g(x)=f(x^2)$ 不是周期函数。

注意这里我们不能先入为主地认为 $g(x)$ 的周期就是 $T$，我们设 $g(x)$ 的周期是 $T'$。

我们的入手点在于 $f(0)$，如果我们能够证明对于任意 $T'$，存在 $f((T'+x)^2) \not=f(x^2)$ （其中有一个是 $f(0)$）就能说明 $g(x)$ 不是周期函数。

$g(0)=f(0^2)=f(0),g(T')=f(T'^2)=f(0)$，推出 $T'^2=kT$，其中 $k \in \mathbb{N}_+$。那么我们下面代入 $T'=\sqrt{kT}$。

接下来考察 $g(\sqrt{T})=f(0)$，$g(\sqrt{T}+T')=f(T+2\sqrt{T\times kT}+kT)=f(2T\sqrt{k})$。

而 $2T\sqrt{k}$ 应该等于 $mT$，其中 $m\in \mathbb{N}_+$。这样说明了 $k$ 是一个完全平方数。

再考察 $g(\sqrt{2T})=f(0),g(\sqrt{2T}+T')=f(2T+2\sqrt{2T \times kT}+kT)=f(2T\sqrt{2k})$。

这显然不是 $T$ 的整数倍，于是出现矛盾！

例题

设 $f(x)$ 在 $(0,+\infty)$ 上定义，$\frac{f(x)}{x} \downarrow$，证明 $f(x_1+x_2) \le f(x_1)+f(x_2)$。

假设 $x_1<x_2$，利用 $x_1,x_2$ 和 $x_1,x_1+x_2$ 之间大小关系……

例题

若 $f(x)$ 满足：

$f(x+1)=2f(x)+k\times 3^x$

若 $f(x)=C(x) \times 2^x+k\times 3^x$，求证 $C(x)$ 周期为 $1$。

从定义出发，即求证 $C(x)=C(x+1)$，而解得 $C(x)=f(x)\times 2^{-x}-k\times(\frac{3}{2})^{-x}$。然后发现就是 $f(x)$ 满足的关系式。