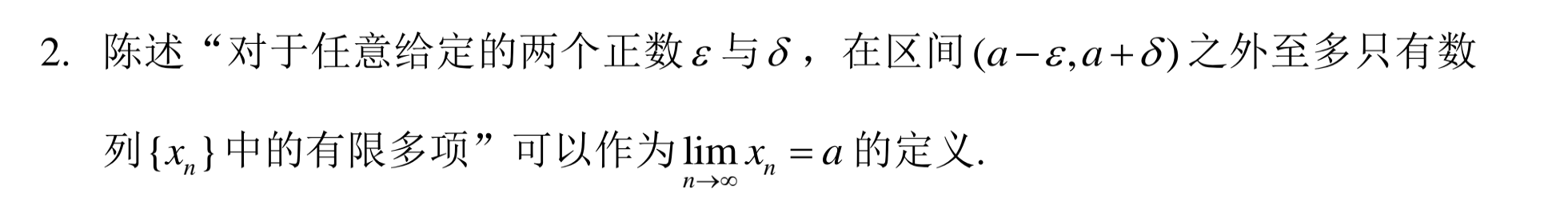高数第三弹 数列的极限

数列的极限

数列极限的定义

例题

$\lim_{n \to +\infty} [\frac{1^2}{n^3}+\frac{2^2}{n^3}+\cdots+\frac{(n-1)^2}{n^3}]$

易知是 $1/3$，如果计准确值为 $f(n)$，再看：

$\lim_{n \to +\infty} [\frac{1^2}{n^3}+\frac{3^2}{n^3}+\cdots+\frac{(2n-1)^2}{n^3}]$

这个显然就是 $8f(2n)-4f(n)$。

其它具有奇数项求极限也可以用这个方法，其实这个比较经典的是运用在求：

$\lim_{n \to +\infty} \sum \frac{1}{n^2}$

已知：

$\lim_{n \to +\infty} \sum \frac{1}{(2n-1)^2}=B$

设上式的值是 $A$，则 $A-A/4=B$，就可以解出来 $A$。

例题

设 $a$ 是实数，而且 $\lim _{n \to +\infty} (x_n-x_{n-1})=a$，证明：

$\lim_{n \to +\infty} \frac{x_n}{n}= a$

例题

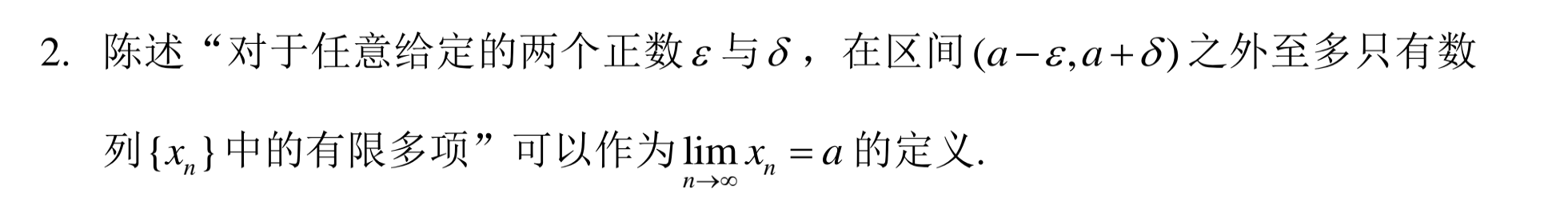
相当于一个有有限元素的数集必然有上确界……

容易漏掉的坑

有 $N=[\log...]$ 的情况，需要考虑底数 $\le1$ 和 $>1$ 两种情况。（根据极限的定义，$N>0$）

一些定义

无穷大量和无穷大

$\forall G>0,\exists N \in \mathbb{Z}_{+},s.t. n>N, |x_n| >G$，称数列 $\{x_n\}$ 为 无穷大量，简称 $x_n$ 为无穷大，记为 $\lim_{n \to \infty} x_n= \infty$。

数列无界

等于数列组成的集合无界。无界和无穷大不等价。

数列极限的性质

唯一性。（模仿唯一性的证明，我们要证某个数列的极限就是 $A$，就说明如果极限是 $B$，两者推出的 $x_n$ 的取值范围不相交。）

有界性。（核心是数列中处于某个邻域范围之外的数的个数是有限的，将数列的元素看成数轴上的点，讨论它们和区间的包含关系，是常用的手段）

对数列极限有影响的只有某项后面的所有项。

保序性，保号性。（核心和有界性的证明相似，都是取一个特定的区间，证明数列之后若干项一定落于这个区间内）

归并性。（反证法，核心与上面相同；另外，我们也经常用到 $n_k \ge k$；如果若干个无穷项的子序列能将整个 $\{x_n\}$ 完全覆盖，那么 $\{x_n\}$ 的极限等于 $A$ 等价于这些子序列的极限都等于 $A$）

数列极限运算的四则法则

$\lim_{ n \to \infty} x_n\lim_{ n \to \infty} y_n=\lim_{ n \to \infty} x_ny_n$

$\lim_{ n \to \infty} x_n /\lim_{ n \to \infty} y_n=\lim_{ n \to \infty} x_n/y_n$

我们证明乘法的性质，可以将 $x_n$ 表示为 $A+\alpha_n$，其中 $A$ 是 $\lim_{n \to \infty} x_n$，$\lim_{n \to \infty} \alpha_n=0$，同理可以设 $y_n=B+\beta_n$，则 $x_ny_n=AB+A\beta_n+B\alpha_n+\alpha_n\beta_n$，通过有界量乘以无穷小=无穷小，无穷小+、*无穷小=无穷小就可以得知。

通过 $\lim_{n\to \infty} 1/y_n \lim_{n \to \infty} y_n=1$ 推知下面的式子。

如何证明当 $x_n \ge 0$ 而且 $\lim_{n \to +\infty} x_n =A \ge 0$，$m$ 为正整数，$\lim_{n \to \infty} \sqrt[m]{x_n}=\sqrt[m]{A}$？关键是将 $(x_n-A)$ 看为 $((\sqrt[m]{x_n})^m-(A)^m)$。

单调有界数列必有极限

将数列中元素看做集合的元素，主要利用：

1. 有界推出有确界。
2. 数集确界的定义。
3. 数列单调递增/递减。

利用这个性质证明时，我们常常采用下面的方法：

1. 假设数列的极限存在，推算出极限可能的值，或者代入几项试试看。
2. 证明数列有界、单调，从而推出极限存在。
3. 推算极限的值，结合数列的界，排除不可能的值，得到最终的答案。

我们利用这个定理时，一定需要讨论数列的单调性，常见的做法除了作差、做商之外，还可以观察 $a_{n+1}$ 的表达式，如果 $a_{n+1}=f(a_n)$。

1. $f(x)$ 单增，则 $a_n$ 单调。具体地，当 $a_1<a_2$，$a_n$ 单增，$a_1>a_2$，$a_n$ 单减。$a_1=a_2$，$a_n$ 为常数。

   怎么证？$a_n=f(a_{n-1}),a_{n-1}=f(a_{n-2})$，归纳知 $a_{n-1},a_{n-2}$ 的大小关系，这个关系保持不变是传递下去的。

2. $f(x)$ 单减，则 $\{a_{2n}\}$ 和 $\{a_{2n-1}\}$ 是单调数列。$f(f(x))$ 单增，同上。由归并性，我们设这两个数列的极限分别为 $A,B$，根据递推式，我们有 $A=f(B),B=f(A)$，需要我们解出来 $A=B$，才能说明极限存在。

3. 另外，根据高中数学的方法，我们可以利用蛛网图直观地观察数列元素的趋势：

   

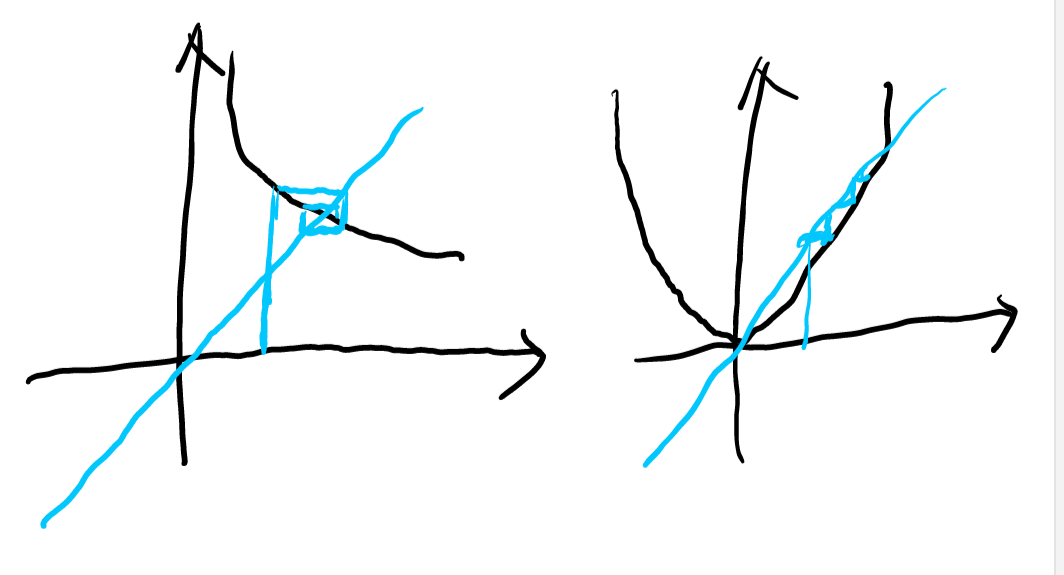
夹逼定理

例题

$\lim_{n \to + \infty} (\frac{1}{n^2+n+1}+\frac{2}{n^2+n+2}+\frac{3}{n^2+n+3}\cdots+\frac{n}{n^2+n+n})=A$

这种一般是放缩分母……

$A>\lim _{n \to +\infty} \sum \frac{i}{n^2+n+n}=\frac{1}{2}$

$A<\lim _{n \to +\infty} \sum \frac{i}{n^2+n} = \frac{1}{2}$

例题

求：

$\lim_{n \to +\infty}\sum_{k=1}^n (\sqrt{1+\frac{k}{n^2}}-1)$

先估计 $\frac{k}{n^2}$ 大约是 $\frac{1}{n}$ 量级，所以我们展开到第二项就足够了，或者直接利用伯努利公式：

$n \to +\infty,\sqrt{1+\frac{k}{n^2}} = 1+\frac{k}{2n^2}$

所以全部加起来就会得到：

$\sum_{k=1}^n \frac{k}{2n^2}=\frac{n(n+1)}{4n^2}\to\frac{1}{4}$

更加严谨的做法我们可以使用夹逼定理。

原式转换为：

$\frac{1}{n} \lim_{n \to +\infty} \sum_{k=1}^n (\sqrt{n^2+k}-n)=\frac{1}{n} \lim_{n \to +\infty} \sum_{k=1}^n \frac{k}{\sqrt{n^2+k}+n}$

$\frac{1}{n} \lim_{n \to +\infty} \sum_{k=1}^n \frac{k}{\sqrt{n^2+k}+n} < \frac{1}{n} \lim_{n \to +\infty} \sum_{k=1}^n \frac{k}{\sqrt{n^2+1}+n} \to \frac{1}{4}$

$\frac{1}{n} \lim_{n \to +\infty} \sum_{k=1}^n \frac{k}{\sqrt{n^2+k}+n} > \frac{1}{n} \lim_{n \to +\infty} \sum_{k=1}^n \frac{k}{\sqrt{n^2+n}+n} \to \frac{1}{4}$

于是证明了原式极限为 $1/4$。

为什么我们要分子有理化？原因是 $\sqrt{n^2+k}+n$ 的影响在分母上比较小。

关于分子有理化，我们也有另外的题目：

$|\sqrt{a^2+b^2}-\sqrt{a^2+c^2}|\le|b-c|$

$|\sqrt{a^2+b^2}-\sqrt{a^2+c^2}|=\frac{|b^2-c^2|}{\sqrt{a^2+b^2}+\sqrt{a^2+c^2}} \le \frac{|b^2-c^2|}{|b|+|c|} \le |b-c|$

由此可见分子有理化是高数中非常常见的思路之一。

闭区间套定理

1. $[a_{n+1},b_{n+1}] \subseteq [a_n,b_n] ,\forall n \in \mathbb{N}_{+}$。
2. $\lim_{n \to \infty}( b_n-a_n)=0$。
3. 则有唯一实数 $\xi$，$a_n \le \xi \le b_n$。

由单调有界数列必有极限，得出 $a_n$ 有极限 $\alpha$，$b_n$ 有下界 $\beta$，由极限的四则运算法则，得 $\beta-\alpha=0$，即 $\alpha=\beta$。

首先，我们取 $\xi=\alpha=\beta$，得到存在这样的 $\xi$（存在性）。

若还存在另外的 $\xi'$ 满足条件，我们证明 $\xi'=\xi$（唯一性）。不妨设 $\xi'<\xi$，我们取 $\varepsilon=\frac{\xi-\xi'}{2}$，则可以满足让 $\xi'$ 不落在 $\xi$ 的邻域之中。这就证明了 $\xi$ 的唯一性。

“压缩”定理

1. $A,L$ 是常数，$0<L<1$。
2. 数列 $\{a_n\}$ 满足：$\exists N \in \mathbb{Z}_{+}$，$\forall n>N$，$|a_{n+1}-A| \le L|a_n-A|$。
3. 证明：$\lim_{n \to \infty} a_n=A$。

运用夹逼定理，易得：

$0\le|a_n-A|\le L^{n-N+1} |a_{N+1}-A|$

得到 $\lim_{n \to \infty}|a_n-A|=0$。

容易发现它其实就是闭区间套定理的一种特殊情况，但是它在实际求极限中还是比闭区间套定理好用的。

B-W 定理

我们研究一个有上下确界 $\sup a,\inf a$的无限项数列 $\{a_n\}$，求证 $\{a_n\}$ 必然有一个收敛子列。

我们观察区间 $[\inf a,\sup a]$，将其分成两个相等的部分 $[\inf a,(\inf a+\sup a)/2],[(\inf a+\sup a)/2,\sup a/2]$，观察 $\{a_n\}$ 落入两个部分中的项的个数，显然这两个个数不可能都为有限项，于是我们任选一个无限项的区间，“抛弃” $\{a_n\}$ 落入另一个区间的其他项，继续分割下去。这样我们可以得到一系列的区间，根据“压缩”定理，就可以说明 $\{a_n\}$ 剩下的项组成的子列是收敛的。

闭区间套定理和其它若干定理的共性

我们通常喜欢讨论实数的连续性，与其相关的是

1. 确界存在定理。这说明了在确界附近的某个（左/右）领域中，实数是连续的。

2. 单调有界数列极限存在。它和确界存在定理本质上是相同的，不过是给无序的数集加上的有序的条件。

3. 闭区间套定理。这个定理本质上是由单调有界数列极限存在推出的，这个定理最重要是说明了这些区间的交集为一点，而且这一点存在，如果实数集不是连续的，就会出现像下图一样的反例。