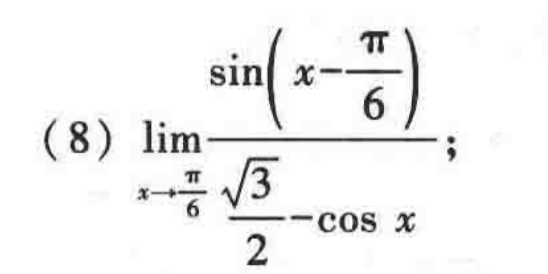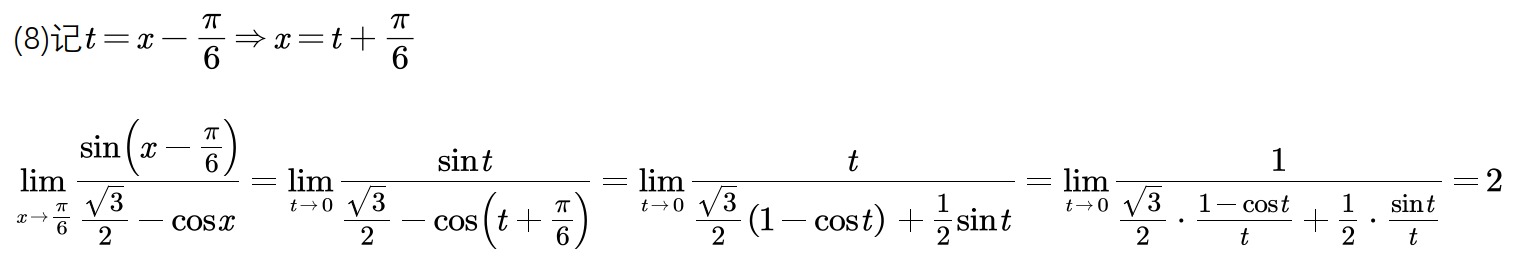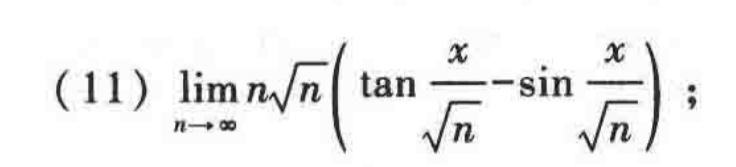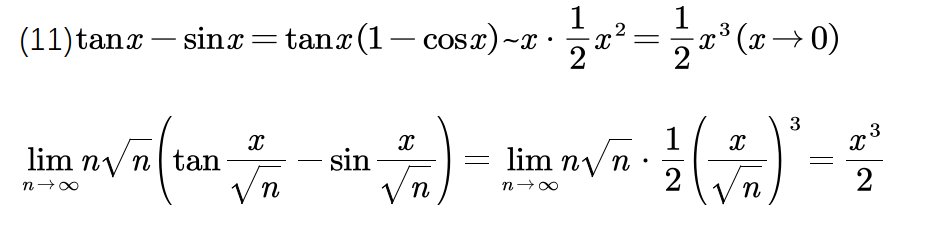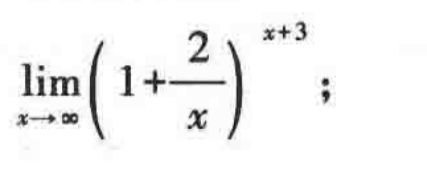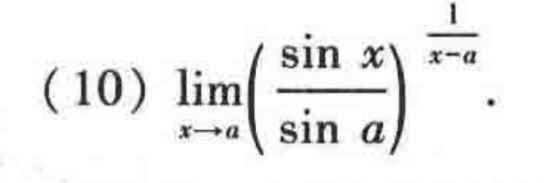定义
存在实数 A,∀ε>0,∃δ>0,0<∣x−a∣<δ 时:
∣f(x)−A∣<ε
含有无穷大的表述类似,这里就不写了。我们算了一下,x 可以趋近的取值有 a,±∞,∞,x0±,而 f(x) 可以趋近的取值有 A,±∞,∞,一共 24 种定义。
注意这里要排除 a 这个点,因此我们说:当 x→0,y=x,x=0;1,x=0 和 y=x 有相同的趋势。
用定义证明,我们通常先分析 ∣f(x)−A∣<ε 对 x 的范围有什么要求,根据这个要求推出 δ。我们也喜欢将 ∣f(x)−A∣ 写成 ∣x−a∣α×g(x) 的形式,然后对 g(x) 进行放缩,如果 g(x) 是 0/0 的形式,还要对分子分母提取公因式。
证明极限是正/负无穷,我们经常放缩,让 f(x) 小于一个趋于负无穷的式子,或是大于一个趋于正无穷的式子。
例题
用定义验证 limx→−∞xx2+1=−1。
我们任意给定 ε,使得 ∣xx2+1+1∣<ε,相当于 ∣x1∣×∣x2+1−x1∣<ε,分析 x→−∞,x2+1−x 大于 2x,于是我们取 X=−2ε1。
海因定理
此定理类似于数列的归并性。
limx→x0f(x)=A(ε,δ) 的充要条件是:
对于任何满足 xn=x0(n=1,2,⋯) 而且 limn→∞xn=x0(U∘(x0),G) 的数列 {xn},都有 limn→∞f(xn)=A(N,U∘(A))。
我们先搭建逻辑链。先证明必要性。要求 limn→∞f(xn)=A,就要这个数列总是有无穷项在 A 的任意邻域之中,而我们现在已经有 limx→x0f(x)=A,说明只要给定一个 A 的邻域,总是能够找到一个 x0 的去心邻域,使得在这个邻域之中的所有 x 的函数值都落于 A 的这个邻域之中,而现在我们利用 limn→∞xn=x0 的定义,给定一个 x0 的去心邻域(题目规定 xn=x0 就保证了去心),使得存在 G,使得任意 i>G,xi 在这个去心邻域之中。逻辑链就是 U∘(A)→δ→ε→U∘(x0)→G→N。
而充分性比较显然,任意取一个数列即可。
利用海因定理证明极限不存在,我们取两个数列 {an},{bn},证明 limf(an)=limf(bn)。
例题
讨论 limx→0+xasinx1 是否存在,存在时取值多少。
可以根据海因定理,说明 a≤0 的情况,极限不存在,根据夹逼定理,说明 a>0 时极限是 0。
函数极限的性质
唯一性
选两个互不包含的区间……或者使用海因定理,可以将数列极限的唯一性平移到函数。
单调有界函数单侧极限存在定理
主要方便在配合海因定理,将数列的一些极限套在函数的极限上。
局部有界性
利用极限的定义不难证明,用海因定理,我们可以选出一系列逐渐压缩的区间,在这些区间中选出一系列点,使它们的函数值趋于正无穷,然后就导出矛盾。
局部保序性
例题
设函数 f(x) 在闭区间 [a,b] 上严格单增,且 f([a,b])=[f(a),f(b)]。
证明:对于任意 x0∈[a,b],有 limx→x0f(x)=f(x0)。
当 x∈[a,x0),f(x) 单增而且有上界,这说明了 limx→x0−f(x) 必然存在,设为 A,则根据极限的保序性,A≤f(x0),下面说明 A<f(x0) 能够推出矛盾:根据极限的定义,我们取 ε=2f(x0)−A,则一定有 δ>0,使得 x∈(x0−δ,x0) 时,f(x)∈(A−ε,A+ε),此时是取不到 [A+ε,f(x0)) 这个区间内的所有值的。所以 limx→x0−=A,同样我们可以说明 limx→x0+=A,所以得证。
局部保号性
复合函数的极限
u→u0limg(u)=g(u0)(εg,δg),x→x0limf(x)=u0(εf,δf)
证明:
x→x0limg(f(x))=g(u0)(ε,δ)
逻辑链:
ε→εg→δg→εf→δf→δ
这说明了我们可以使用变量替换:
x→alimf[φ(x)]=A→(u=φ(x))u→blimf(u)=A
夹逼定理
运用海涅定理,就可以关联数列的性质和函数的性质。
一系列三角重要不等式
(怎么推的?
1.单位圆,推出 cosx<xsinx<1
2.夹逼定理 0<1−xsinx<1−cosx=2sin22x≤2x2)
得到:
∣sinx∣≤∣x∣,∀x∈R0≤1−cosx≤2x2,∀x∈R
无穷小的比较
几个重要的概念:高阶/低阶;同阶;等价。
同阶、等价的传递性。
标准无穷小:x→a:(x−a),n→+∞:n1。
并非任意两个无穷小可以互相比较,当且仅当它们相除极限存在,比如 xsinx1 和 x 就无法比较。
阶数、主部:
若 limx→aα(x)=0,且存在常数 c=0,k>0,使得:
x→alim(x−a)kα(x)=c
则称当 x→a 时, α(x) 是标准无穷小 x−a 的 k 阶无穷小,简称 α(x) 是 k 阶无穷小,而称 c(x−a)k 是 α(x) 的主部。称为 α(x)∼c(x−a)k(x→a)(等价),而且 α(x)=c(x−a)k+o((x−a)k)。
若 α(x) 是多项式,就看指数最小的那一项。
常见的等价无穷小
x→0 时:
ln(1+x)∼x,ex−1∼x
sinx∼x,tanx∼x,1−cosx∼21x2arcsinx∼x,arctanx∼x
(换元,limxarcsinx=limsinuu⋯ )
我们再复习一些常见的三角函数名称:
csc:1/sin,sec:1/cos
(1+x)α∼1+αx
这个证明方法比较多,可以用定义,也可以:
limx(1+x)α−1=limαln(1+x)eαln(1+x)−1×xαln(1+x)=α
也可以:
x→0lim(1+x)α=exp(αx→0limln(1+x))∼exp(αx)∼1+αx
等价无穷小为什么可以在乘除法互相替换?原因在于定义:limα(x)/α~(x)=1……
但是涉及到加减法时,可能就会有反例,这个反例在于无穷大-无穷大是不确定的值,无穷大+负无穷大也是不确定的值。比如 limx→0+(1+x1−(x1−1))=limx→0+(1+x1)−limx→0+(x1−1)=+∞−+∞=2。
我们计算:
x→0limx3tanx−sinx
如果我们简单替换 tanx,sinx 为 x,会发现答案是 0,而这个显然是不对的,因为:
x→0limx3tanx−sinx=x→0limtanx×x31−cosx=x→0limx×x321x2=21
原因是 tanx/x3,sinx/x3 都是无穷大,直接替换是不合法的。(或者叫损失精度)
若 f(x) 主部 C1(x−x0)k1,g(x) 主部 C2(x−x0)k2,我们可以讨论 f(x)−g(x) 的主部。
当 k1=k2,指数较小的决定主部。
当 k1=k2,若 C1=C2,说明阶数还是 k1/k2,决定了主部。但 C1=C2,就无法确定主部。
处理函数极限的常用手段
-
提取公因式,对于分母分子都是多项式的还好说,如果对于上下包含根式的 0/0 型表达式怎么办?
如果根式是类似于 f(x0)−g(x0)=0 的情况(f,g 是多项式),可以有理化形成 f(x0)+g(x0)f(x0)−g(x0)。
这样就可以发现 f(x0)−g(x0) 可以提取出一个 (x−x0) 的公因式。
-
提取“常量”。
-
等价无穷小的替换。
-
换元的技巧:比如替换 x→a 为 u→0,其中 u=x−a 等等。
-
和差化积,积化和差。好处是创造出一个常量。
-
指对转换。例如:
x→∞lim(x22+cosx1)x2=explimx2ln(x22+cosx1−1+1)=explimx2(x22−2x21)=explim23=e23
几道不错的例题
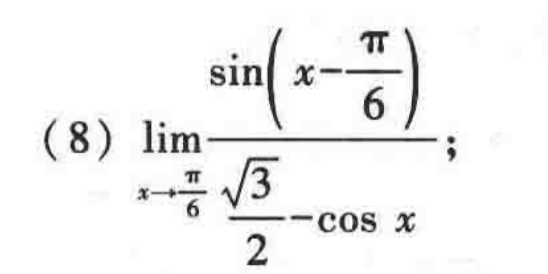
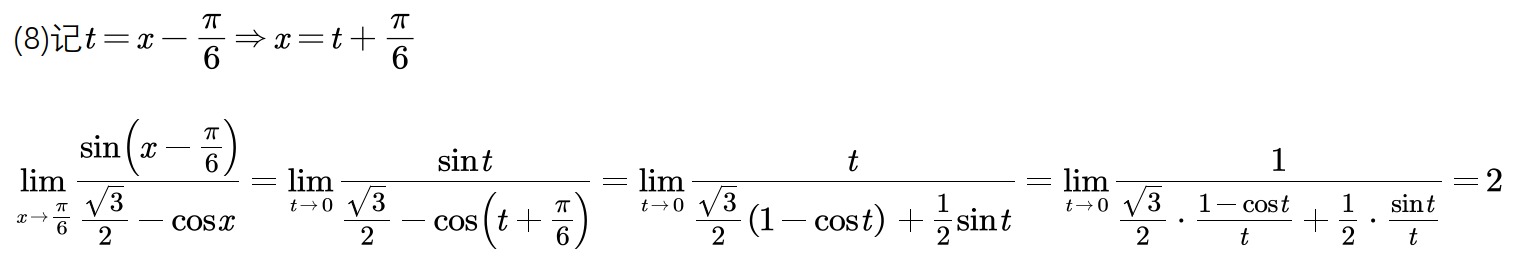
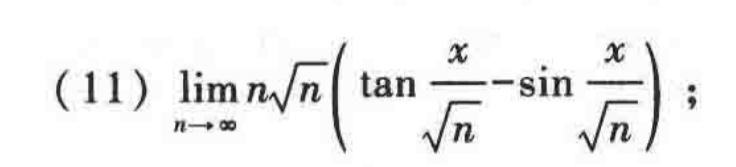
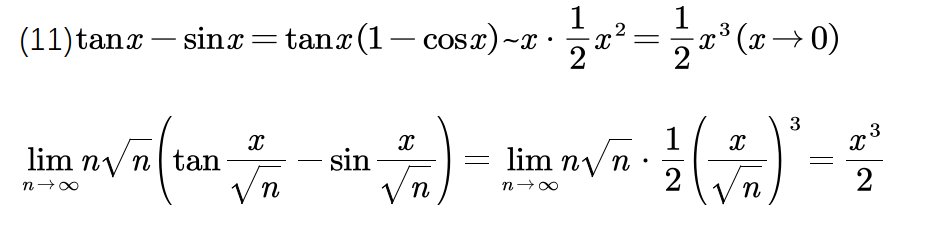
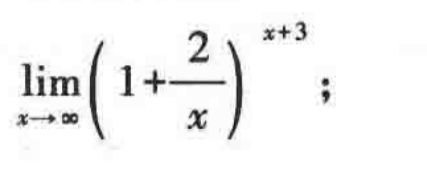

注:6/x 相当于无穷小,可以省去,或者说,e无穷小=1。
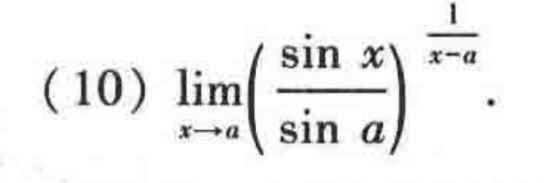
x→alim(sinasinx)x−a1=(t=x−a)expt→0limt1ln(sinasin(t+a))=expt→0limt1(sinasin(t+a)−1)=expt→0limt1(sint×cota+cost−1)=ecota