布尔表达式

Boolean Operations and Expressions (布尔运算和表达式)

Laws and Rules of Boolean Algebra (布尔代数的运算法则)

交换律 Commutative Law

结合律 Associative Law

分配率 Distributive Law

1. $A+0=A,A+1=1$

2. $A\cdot 0=0,A \cdot 1=A$

3. $A+A=A,A+\overline{A}=1$

4. $A\cdot A=A,A\cdot \overline{A}=0$

5. $A+AB=A$（基础）

6. $A+\overline{A}B=A+B$

   因为 $A+\overline{A}B=A+AB+\overline{A}B=A+B$

7. $(A+B)(A+C)=A+BC$

   因为 $(A+B)(A+C)=AA+AC+AB+BC=A+AC+AB+BC$

   $=A+AB+BC=A+BC$。

8. $AB+\overline{A}C+BCD=AB+\overline{A}C$

   $AB+\overline{A}C+BCD=AB+\overline{A}C+(A+\overline{A})BCD$

   $=AB(1+CD)+\overline{A}C(1+BD)=AB+\overline{A}C$

   用韦恩图证明，可以知道 $BCD \in BC \in AB+\overline{A}C$。

9. $A\overline{B}+\overline{A}B=A\oplus B$。

10. $AB+\overline{AB}=\overline{A\oplus B}$。

都可以用韦恩图证明，韦恩图的本质是枚举真值。

区分 Boolean Addition 和 mod-2 addition，后者是异或。

对偶表达式的概念：

德摩根定律（DeMorgan’s Theorems）

1. $\overline{XY}=\overline{X}+\overline{Y}$。
2. $\overline{X+Y}=\overline{X}\, \overline{Y}$。（$\overline{XY} \not= \overline{X} \, \overline{Y}$）

从上往下化简

Boolean Analysis of Logic Circuits (逻辑电路的布尔分析)

逻辑电路可以用真值表来描述。

使用布尔代数进行化简。

Simplification Using Boolean Algebra (利用布尔代数化简)

标准形式 Standard Forms

• SOP sums-of-products A+AB, AB+ABC, A+C ̅DE+B ̅CD ̅
• POS products-of-sums A(A+B), (A+B)(A ̅+C), B(A+B ̅+C)(B+D)

A minterm (最小项) is a product of all variables in the domain.

A maxterm (最大项) is a sum of all variables in the domain.

In standard SOP or sum-of-minterms form, each product term involves all variables in the domain. $ AB ̅CD + A ̅B ̅CD + ABC ̅D ̅ $

In standard POS or sum-of-maxterms form, each sum term involves all variables in the domain. (A+B ̅+C)(A ̅+B ̅+C)(A+B+C ̅ )

Conversion to Standard SOP Form

Multiply each nonstandard product term by a sum term of a missing variable and its complement.

Conversion to Standard POS Form

1. Add, to each nonstandard sum term, a product term of a missing variable and its complement.
2. Factorize the sum term. $A+BC=(A+B)(A+C)$.

$F=\sum m(0,2,3,4,6,8,10,11,12,14)$

$11 \Rightarrow (1011)_{(2)} \Rightarrow (ABCD)_{(2)}$

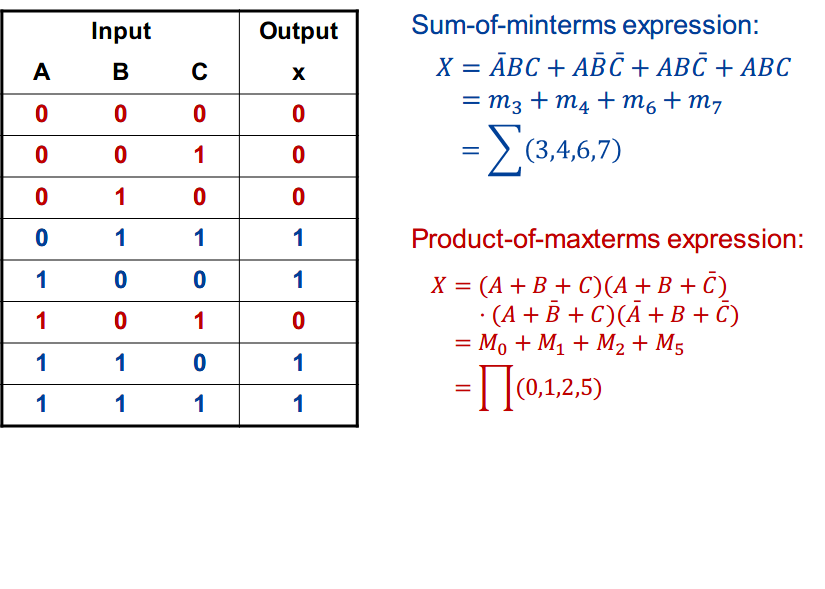
Boolean Expressions and Truth Tables (布尔表达式及真值表)

The Karnaugh Map (卡诺图)

卡诺图用于化简布尔表达式。

The Karnaugh map (or K-map for short) was invented in 1953 by Maurice Karnaugh at Bell Labs.

The Karnaugh map provides a systematic method for simplifying Boolean expressions to produce the simplest SOP or POS expression.

A Karnaugh map is a two-dimensional array of cells in which each cell is a binary value combination of the input variables.

The cell in Karnaugh map are arranged so that there is only a single-variable change between adjacent cells.

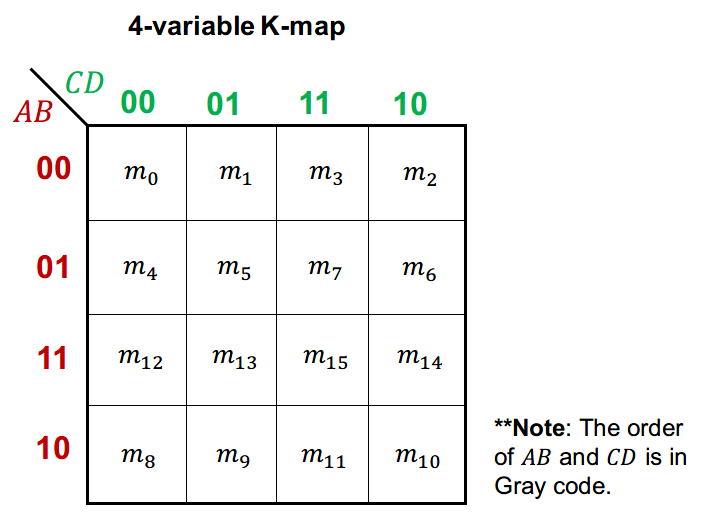
Cell Adjacency: Definition.

To obtain the Karnaugh map of a standard SOP expression, one places a 1 in each cell where the product term (i.e., minterm) is 1.

Karnaugh Map SOP Minimization (卡诺图的积之和最小化)

Minimization of an SOP expression is to find an SOP expression that contains the fewest possible terms with the fewest possible variables per term.

It requires two steps:

1. Group the 1s on the map.

   a. A group contains 1, 2, 4, 8 or 16 cells that are adjacent.

   b. Always include the largest possible number of 1s in a group in accordance with rule a).

   c. Each 1 on the map must be included in at least one group.

   

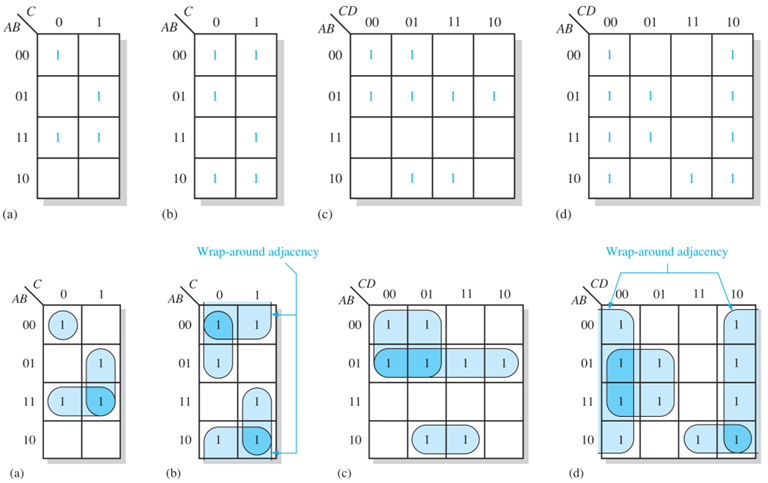
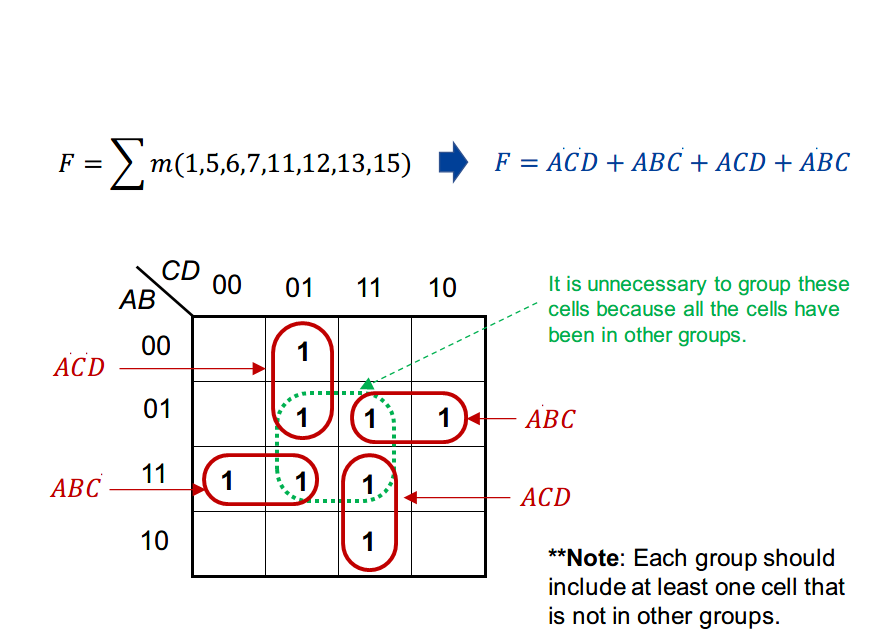
2. Determine the minimum SOP expression.

   1. Create a product term for each group of 1’s.

      Group size = $\log_2(2^{|D|}/|\mathrm {cell}|)$.

   2. Sum all the product terms.

Karnaugh Map POS Minimization (卡诺图的和之积最小化)

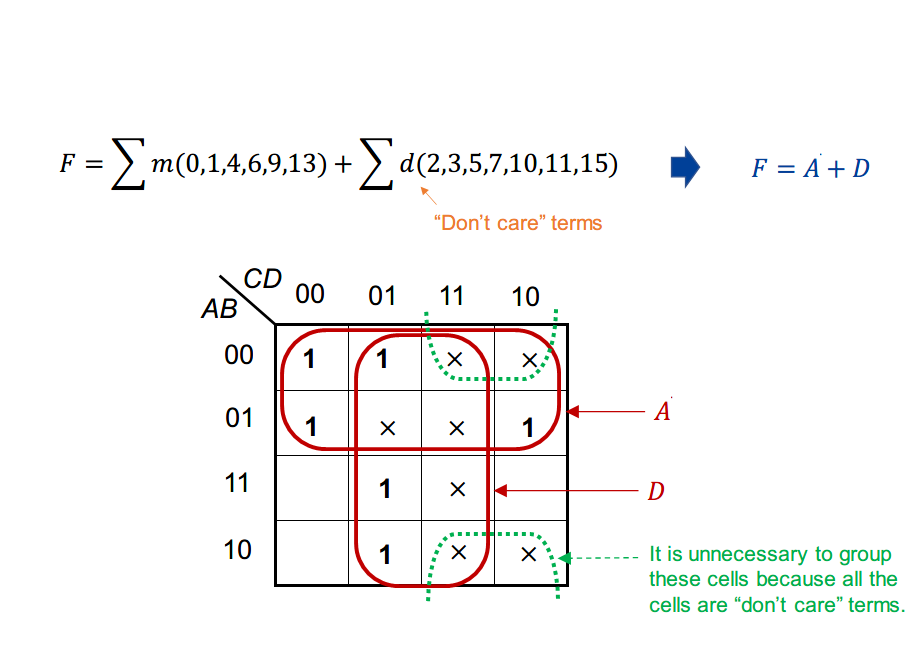
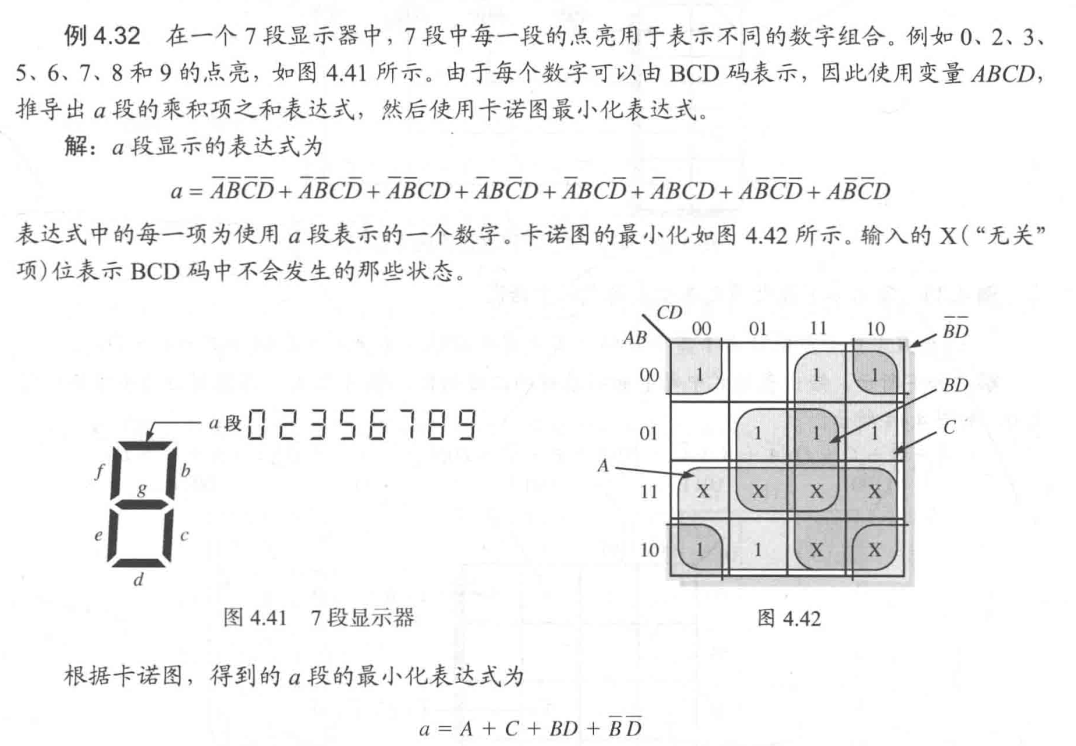
Don’t Care Terms

A “don’t care” term is a combination of input literals that can be assigned a 0 or a 1 on the Karnaugh map.

A “don’t care” term indicates a situation that cannot happen or has no matter. It is denoted by “×” in the truth table and the Karnaugh map.

E.g. Minimize the expression: $X=A\overline{B}D+\overline{ABC}D+\overline{B}CD+\overline{A\overline{B}+C}(B+D)$.

结合卡诺图和利用布尔代数化简。

Mapping a Standard POS Expression

To obtain the Karnaugh map of a standard POS expression, one places a 0 in each cell where the sum term (i.e., maxterm) is 0.

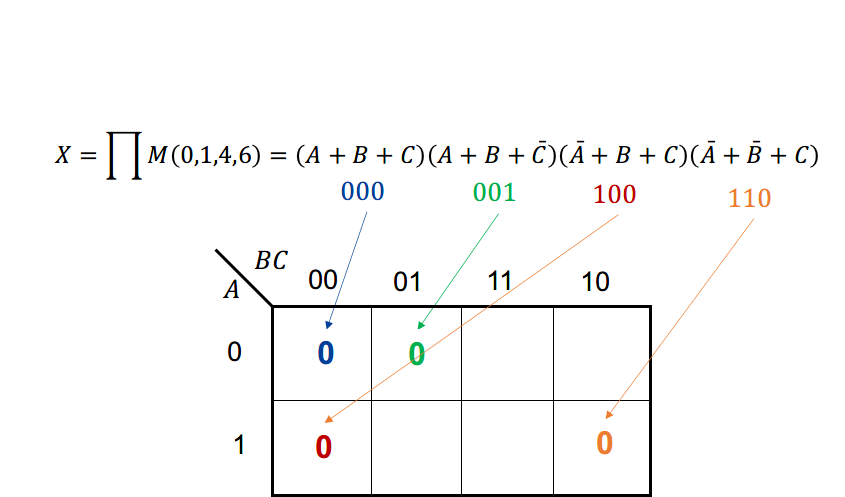
1. Group the 0s in the map.
2. Determine the minimum POS expression.

Conversion Between POS and SOP

$F=\prod M(S)=\sum m(0\sim2^{n-1}-S)$

SOP $\Leftrightarrow$ POS for fewer gates.

The Quine-McCluskey Method

The Quine-McCluskey method (QMC) was developed by Willard V. Quine in 1952 and extended by Edward J. McCluskey in 1956.

It is a formal tabular method for applying the Boolean distributive law: to find minimum common factors.

1. Write the function in standard SOP form.
2. Group the minterms according to the number of 1s.

NP Problem.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127

#include <bits/stdc++.h>
#define N 50
#define M 4
using namespace std;
struct term{
	vector<int>s;
};
term to2(int x){
	vector<int>s;
	for (int i=0;i<M;++i) s.push_back(x&1),x>>=1;
	reverse(s.begin(),s.end());
	return term{s};
}
int num1(term t){
	int cnt=0;
	for (int i=0;i<t.s.size();++i) cnt+=t.s[i]!=0;
	return cnt;
}
bool simp(term x,term y,int &pos){
	int cnt=0;
	for (int i=0;i<x.s.size();++i){
		if (x.s[i]!=y.s[i]){
			if (x.s[i]+y.s[i]!=1){
				return false;
			}
			else{
				cnt++;
				pos=i;
			}
		}
	}
	return cnt==1;
}
vector<term>terms;
vector<term>g[N];
bool used[N][N];
int main(){
	int n;
	cin>>n;
	for (int i=0;i<n;++i){
		int x;
		cin>>x;
		terms.push_back(to2(x));
	}
//	for (int i=0;i<terms.size();++i){
//		for (int j=0;j<terms[i].s.size();++j){
//			cout<<terms[i].s[j]<<" ";
//		}
//		cout<<endl;
//	}
	while (true){
		int lsize=terms.size();
		for (int i=0;i<N;++i) g[i].clear();
		for (int i=0;i<N;++i) for (int j=0;j<N;++j) used[i][j]=false;
		for (int i=0;i<terms.size();++i){
			g[num1(terms[i])].push_back(terms[i]);
//			cout<<"num1:"<<num1(terms[i])<<endl;
		}
		terms.clear();
		bool have_simp=false;
		for (int i=0;i<N-1;++i){
			for (int j=0;j<g[i].size();++j){
				bool simplified=false;
				for (int k=0;k<g[i+1].size();++k){
					int pos=0;
//						if (!used[i+1][k] && simp(g[i][j],g[i+1][k],pos)){
					if (simp(g[i][j],g[i+1][k],pos)){
						simplified=true;
						have_simp=true;
						used[i][j]=used[i+1][k]=true;
						term temp=g[i][j];
						temp.s[pos]=2;
						terms.push_back(temp);
						cout<<"-";
						for (int t=0;t<g[i][j].s.size();++t){
							cout<<g[i][j].s[t]<<" ";
						}
						cout<<endl;
						cout<<"-";
						for (int t=0;t<g[i+1][k].s.size();++t){
							cout<<g[i+1][k].s[t]<<" ";
						}
						cout<<endl;
						cout<<"-";
						for (int t=0;t<temp.s.size();++t){
							cout<<temp.s[t]<<" ";
						}
						cout<<endl;
					}
				}
				if (!simplified && !used[i][j]){
					terms.push_back(g[i][j]);
				}
			}
		}
		for (int i=0;i<terms.size();++i){
			for (int j=0;j<terms[i].s.size();++j){
				cout<<terms[i].s[j]<<" ";
			}
			cout<<endl;
		}
		cout<<"------------------"<<endl;
		if (!have_simp) break;
//		if (terms.size()==lsize){
//			break;
//		}
	}
	cout<<"------------------"<<endl;
	for (int i=0;i<terms.size();++i){
		for (int j=0;j<terms[i].s.size();++j){
			cout<<terms[i].s[j]<<" ";
		}
		cout<<endl;
	}
}
/*
8
1
4
3
5
10
12
13
15
*/

NOR-NOR expression