定积分的几何意义

平面图形的面积

$A=\int_{a}^b [f(x)-g(x)]\mathrm d x$

参数方程：

$A=\int_a^b y\mathrm dx=\int_a^b y(t)x'(t)\mathrm d t$

例如，利用椭圆的参数方程表示形式，可以比较简便地得到椭圆的面积。

极坐标：

可以转化为参数方程，也可以考虑 $\mathrm d \theta$ 的曲边扇形的面积。

$A=\int_\alpha^\beta r^2(\theta)\mathrm d \theta$

求极坐标面积，还要利用好对称的关系，比如关于 $x$ 轴对称，关于 $\pi/2$ 对称等等。

注意，我们还可转化视角，对 $y$ 积分，例如：求 $y=\arctan x,y=\arctan (x+1)$ 之间面积：

$S=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} (\tan y-(\tan y-1) \mathrm)d y$

体积问题

$V=\int_a^b A(x)\mathrm d x$

称为薄片法或者扁柱体法。

旋转体体积：

$V_x=\pi\int_a^b f^2(x)\mathrm d x$

考虑 $\Delta V=[\pi(x+\Delta x)^2-\pi x^2]$，得到 $\mathrm d V=2\pi xf(x)\mathrm d x$

则：

$V=2\pi\int_a^b xf(x)\mathrm d x$

弧长问题

利用 $\mathrm d s=\sqrt{\mathrm d x^2+\mathrm d y^2}$。

极坐标情形：$x=r(\theta)\cos \theta,y=r(\theta)\sin\theta$。

$\mathrm d s=\sqrt{r^2(\theta)+r'^2(\theta)}\mathrm d \theta$

割补法

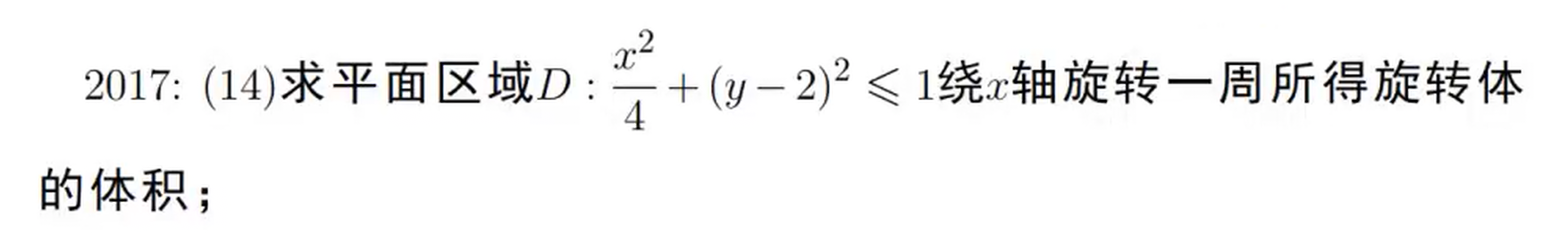
最上面旋转减去最下面旋转，还可以利用重心走过的路程。