例题 2

求 $\cos\frac{\pi}{11}\cos\frac{2\pi}{11}\cos\frac{3\pi}{11}\cos\frac{4\pi}{11}\cos\frac{5\pi}{11}$。

令 $S$ 等于上述式子，令 $T=\sin\frac{\pi}{11}\sin\frac{2\pi}{11}\sin\frac{3\pi}{11}\sin\frac{4\pi}{11}\sin\frac{5\pi}{11}$。

于是 $ST=\frac{1}{32}\sin\frac{2\pi}{11}\sin\frac{4\pi}{11}\sin\frac{6\pi}{11}\sin\frac{8\pi}{11}\sin\frac{10\pi}{11}$。

转换为 $ST=\frac{1}{32}T$，所以 $S=\frac{1}{32}$。

知识点 1

三角中常见的裂项：

$\begin{aligned} \frac{\sin\alpha}{\cos(\beta+\alpha)\cos\beta} &= \frac{\sin(\alpha+\beta)\cos\beta-\cos(\alpha+\beta)\sin\beta}{\cos(\beta+\alpha)\cos\beta}\\ &= \tan(\alpha+\beta)-\tan\beta \end{aligned} \\ \Rightarrow \frac{1}{\cos(\beta+\alpha)\cos\beta}=\frac{\tan(\alpha+\beta)-\tan\beta}{\sin\alpha}$

对 $\sin$ 一波操作也可以得到类似的结论。

$\begin{aligned} &\cos(\alpha)+\cos(\alpha+\beta)+\cos(\alpha+2\beta)+\cdots+\cos(\alpha+n\beta) \end{aligned}$

对于 $\cos(\alpha)$ 可以转换为：

$\frac{\sin(\alpha+\beta/2)-\sin(\alpha-\beta/2)}{2\sin\beta/2}$

每个都如此转换，便可裂项。

$\tan(\alpha+\beta)\tan\alpha=\frac{\tan({\alpha+\beta})-\tan \alpha}{\tan{\beta}}$

$\begin{aligned} &\frac{1}{\sin2x}\\ =&\frac{2\cos^2x-\cos2x}{\sin2x}\\ =&\frac{2\cos^2x}{2\sin x\cos x}-\frac{\cos 2x}{\sin 2x}\\ =&\frac{1}{\tan x}-\frac{1}{\tan 2x} \end{aligned}$

知识点 2

$\cos n\theta=f_n(\cos\theta)$

求 $f_n(x)$。

常见的思路是递推：

$\cos(n+1)\theta=\cos(n+1)\theta+\cos(n-1)\theta-\cos(n-1)\theta=2\cos n\theta\cos\theta-\cos(n-1)\theta$

相当于 $f_{n+1}(x)=2xf_n(x)-f_{n-1}(x)$。

如何完全分解 $f_n(x)$，常见的思路是找 $f_n(x)=0$ 的解。

$n\theta=\frac{\pi}{2}+2k\pi \Rightarrow\theta_k=\frac{\frac{\pi}{2}+2k\pi}{n}$

由上面的递推公式知道最高项的系数是 $2^{n-1}$。

于是 $f_n(x)=2^{n-1}\prod_{k=1}^n(x-\theta_k)$。

知识点 3

反三角函数

常见的思路是换元，如：

求 $f(x)=x+\frac{1}{2}\arccos x$ 的最大值。

令 $\theta=\arccos x$，则 $x=\cos \theta$。

换元之后可以使用和角公式、差角公式处理，得到 $\theta$ 角之间的关系。

知识点 4

三角函数的降次。

二倍角公式：$\cos2\theta=2\cos^2\theta-1$。

推出 $\cos^2\theta=\frac{\cos2\theta+1}{2}$。

三倍角公式：$\cos3\theta=4\cos^3\theta-3\cos\theta$。

推出 $\cos^3\theta=\frac{\cos3\theta+3\cos\theta}{4}$。

其背景也是齐次化。

知识点 5

同角齐次化转为正切。通常使用 $1=\sin^2x+\cos^2x$，或者 $1=\sqrt{\sin^2x+\cos^2x}$。

$\sin\beta=\sin\alpha\cos(\alpha+\beta),\tan\beta=?,\rm max=?$

将 $\cos(\alpha+\beta)$ 拆解，两边同除 $\cos\beta$，整理得：

$\tan\beta=\frac{\sin\alpha\cos\alpha}{1+\sin^2\alpha}=\frac{\sin\alpha\cos\alpha}{\cos^2\alpha+2\sin^2\alpha}=\frac{\tan\alpha}{1+2\tan^2\alpha} \le\frac{\sqrt2}{4}$

知识点 6

$\sin x+\cos x=t$ 的换元，不解释。

知识点 7

线性方程组的处理。

技巧：平方和+平方差，二倍角公式+和差化积。

三角形中的三角函数

知识点 8

切化弦

$(\cot A+ \cot B + \cot C)_{\min}=?$

$\cot A+ \cot B +\cot C=\frac{\sin C}{\sin A\sin B} +\cot C\ge \frac{\sin C}{\sin^2(\frac{A+B}{2})}+\cot C=\frac{2\sin\frac{C}{2}\cos{\frac{C}{2}}}{\cos^2\frac{C}{2}}+\frac{1-\tan^2\frac{C}{2}}{2\tan\frac{C}{2}}$

知识点 9

三角恒等式。

$\tan A+\tan B+\tan C=\tan A\tan B\tan C \Rightarrow \cot A\cot B+\cot B \cot C+\cot A \cot C=1$

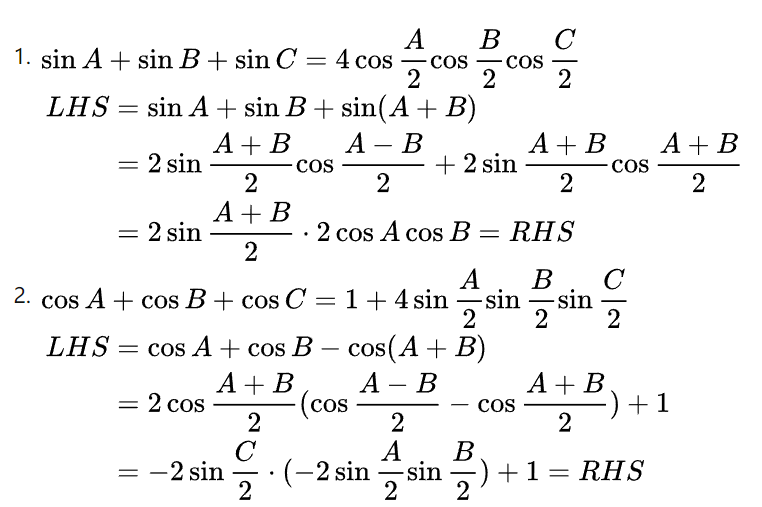
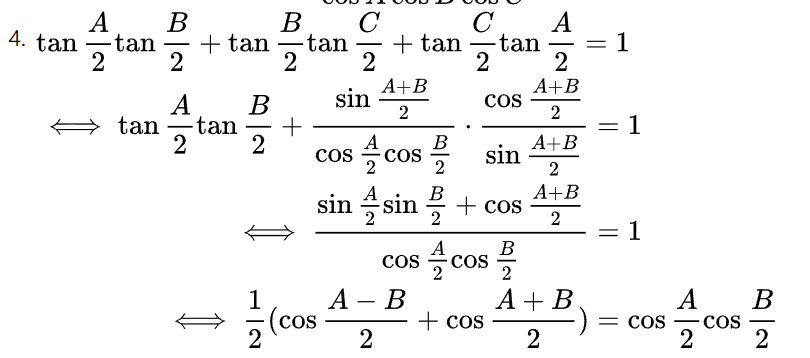
切化弦的操作。

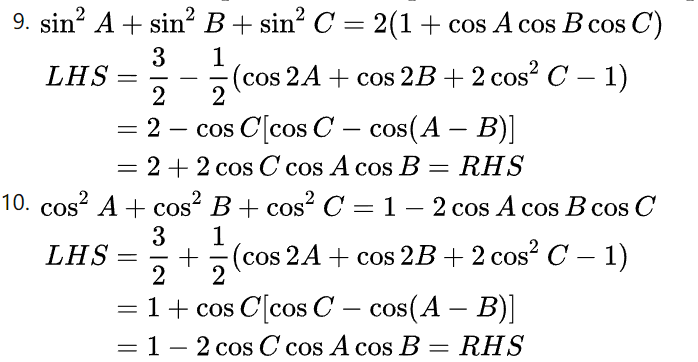
降次的思想+和差化积。